Árvore binária

Uma simples árvore binária de tamanho 9 e altura 3, com um nó raiz de valor 2. A árvore acima não está balanceada (elemento 5 possui 2 filhos a direita e nenhum a esquerda), nem está ordenada - notar que não é uma árvore binária de procura.

Uma árvore binária é uma estrutura de dados caracterizada por:

• Ou não tem elemento algum (árvore vazia).
• Ou tem um elemento distinto, denominado raiz, com dois ponteiros para duas estruturas diferentes, denominadas subárvore esquerda e subárvore direita.

Perceba que a definição é recursiva e, devido a isso, muitas operações sobre árvores binárias utilizam recursão. É o tipo de árvore mais utilizado na computação. A principal utilização de árvores binárias são as árvores binárias de busca

Definições para árvores binárias

Os nós de uma árvore binária possuem graus zero, um ou dois. Um nó de grau zero é denominado folha.

Em uma árvore binária, por definição, cada nó poderá ter até duas folhas, sendo que ela se compara com a ABB (árvore binária de busca), apesar de não ter a propriedade da mesma ("na abb, existe uma regra na inserção").

A profundidade de um nó é a distância deste nó até a raiz. Um conjunto de nós com a mesma profundidade é denominado nível da árvore. A maior profundidade de um nó, é a altura da árvore.

Uma árvore "estritamente binária" é uma árvore na qual todo nó tem zero ou duas folhas.

Existem autores, porém, que adotam essa definição para o termo quase completa, e utilizam o termo completa apenas para árvores em que todos os níveis têm o máximo número de elementos.

Definições em teoria dos grafos

Em teoria dos grafos, uma árvore binária é definida como um grafo acíclico, conexo, dirigido e que cada nó não tem grau maior que 2. Assim sendo, só existe um caminho entre dois nós distintos.

E cada ramo da árvore é um vértice dirigido, sem peso, que parte do pai e vai para o filho.

Inserção

O algoritmo da inserção em árvores binárias são facilmente implementadas através de função recursiva.

Algoritmo da inserção em C:

 void inserir(struct No **pRaiz, int numero){
     if(*pRaiz == NULL){
* pRaiz = (struct No *) malloc(sizeof(struct No));
         (*pRaiz)→pEsquerda = NULL;
         (*pRaiz)→pDireita = NULL;
         (*pRaiz)→numero = numero;
     }else{
         if(numero <(*pRaiz)→numero)
              inserir(&(*pRaiz)→pEsquerda, numero));
         else
              inserir(&(*pRaiz)→pDireita, numero));
     }
 }

Algoritmo em C++:

template <typename T>
BSTree<T> *BSTree<T>::insert(T data)
{
  if (!this)
    return new BSTree(data);

  if (data > this->data)
    this->right = this->right->insert(data);
  else
    this->left = this->left->insert(data);

  return this;
}

Algoritmo da inserção em Java:

public class Arvore {

    public No raiz;

    class No {
        Integer valor;
        No filhoEsquerdo;
        No filhoDireito;

        public No(Integer valor) {
            this.valor = valor;
        }
    }

    public No inserir(Integer valor) {
        return this.inserir(new No(valor), raiz);
    }

    private No inserir(No novo, No anterior) {
        if (raiz == null) {
            raiz = novo;
            return raiz;
        }

        if (anterior != null) {
            if (novo.valor <= anterior.valor) {
                anterior.filhoEsquerdo = this.inserir(novo, anterior.filhoEsquerdo);
            } else if (novo.valor > anterior.valor) {
                anterior.filhoDireito = this.inserir(novo, anterior.filhoDireito);
            } else {
                return null;
            }
        } else {
            anterior = novo;
        }

        return anterior;
    }
}

Algoritmo da inserção em C#:

public class Node{
    public Node(int value){
        Value = value;
    }
    public decimal Value { get; set; }
    public Node Esq { get; set; }
    public Node Dir { get; set; }
}

class Tree {
    private Node root;
    public Tree(int value){
        root = new Node(value);
    }
    public void Add(int value){
        Add(null, value);
    }
    protected virtual void Add(Node node, int value){
        if (node == null)
            node = root;
        if (value < node.Value){
            if (node.Esq == null)
                node.Esq = new Node(value);
            else
                Add(node.Esq, value);
        }else{
            if (node.Dir == null)
                node.Dir = new Node(value);
            else
                Add(node.Dir, value);
        }
    }
}

Algoritmo da inserção em Python:

def insere(raiz, nodo):
    if raiz is None:
        raiz = nodo

    elif raiz.chave < nodo.chave:
        if raiz.direita is None:
            raiz.direita = nodo
        else:
            insere(raiz.direita, nodo)

    else:
        if raiz.esquerda is None:
            raiz.esquerda = nodo
        else:
            insere(raiz.esquerda, nodo)

Percursos em árvore

Existem quatro tipos de percursos: Percurso em ordem simétrica (em-ordem), pré-ordem, pós-ordem e em-nível.

Ordem simétrica

O algoritmo recursivo desse percurso em C é:

 void emOrdem(struct No *pNo) {
     if(pNo != NULL) {
         emOrdem(pNo→pEsquerda);
         visita(pNo);
         emOrdem(pNo→pDireita);
     }
 }

O algoritmo recursivo desse percurso em C++ é:

void ArvoreBinaria :: EmOrdem (No *inicio) {
    if (inicio != NULL) {
        this->EmOrdem (inicio->esquerdo);
        cout << inicio->valor << " ";
        this->EmOrdem (inicio->direito);
    }
}

O algoritmo recursivo desse percurso em Java é:

public void emOrdem(No no) {
    if (no != null) {
        emOrdem(no.filhoEsquerdo);
        System.out.println(no.valor);
        emOrdem(no.filhoDireito);
    }
}

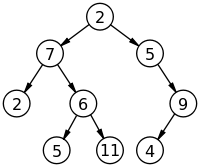
Para a árvore acima, o percurso seria: 2, 7, 5, 6, 11, 2, 5, 4, 9. Veja a linha de execução:

• emOrdem(2→esq)
  • emOrdem(7→esq)
    • emOrdem(2→esq)
    • visita(2)
    • emOrdem(2→dir)
  • visita(7)
  • emOrdem(7→dir)
    • emOrdem(6→esq)
      • emOrdem(5→esq)
      • visita(5)
      • emOrdem(5→dir)
    • visita(6)
    • emOrdem(6→dir)
      • emOrdem(11→esq)
      • visita(11)
      • emOrdem(11→dir)
• visita(2)
• emOrdem(2→dir)
  • emOrdem(5→esq)
  • visita(5)
  • emOrdem(5→dir)
    • emOrdem(9→esq)
      • emOrdem(4→esq)
      • visita(4)
      • emOrdem(4→dir)
    • visita(9)
    • emOrdem(9→dir)

Pré-ordem

O algoritmo recursivo desse percurso em C é:

 void preOrdem(Struct No *pNo){
     if(pNo != NULL){
         visita(pNo);
         preOrdem(pNo→pEsquerda);
         preOrdem(pNo→pDireita);
     }
 }

O algoritmo recursivo desse percurso em C++ é:

void ArvoreBinaria  :: PreOrdem (No *inicio) {
    if (inicio != NULL) {
        cout << inicio->valor << " ";
        this->PreOrdem (inicio->esquerdo);
        this->PreOrdem (inicio->direito);
    }
}

O algoritmo recursivo desse percurso em Java é:

public void preOrdem(No no) {
    if (no != null){
        System.out.println(no.valor);
        preOrdem(no.filhoEsquerdo);
        preOrdem(no.filhoDireito);
    }
}

Para a árvore acima, o percurso seria: 2, 7, 2, 6, 5, 11, 5, 9 e 4. Veja a linha de execução:

• visita(2)
• preOrdem(2→esq)
  • visita(7)
  • preOrdem(7→esq)
    • visita(2)
    • preOrdem(2→esq)
    • preOrdem(2→dir)
  • preOrdem(7→dir)
    • visita(6)
    • preOrdem(6→esq)
      • visita(5)
      • preOrdem(5→esq)
      • preOrdem(5→dir)
    • preOrdem(6→dir)
      • visita(11)
      • preOrdem(11→esq)
      • preOrdem(11→dir)
• preOrdem(2→dir)
  • visita(5)
  • preOrdem(5→esq)
  • preOrdem(5→dir)
    • visita(9)
    • preOrdem(9→esq)
      • visita(4)
      • preOrdem(4→esq)
      • preOrdem(4→dir)
    • preOrdem(9→dir)

Pós-ordem

O algoritmo recursivo desse percurso em C é:

 void posOrdem(Struct No *pNo){
     if(pNo != NULL){
         posOrdem(pNo→pEsquerda);
         posOrdem(pNo→pDireita);
         visita(pNo);
     }
 }

O algoritmo recursivo desse percurso em C++ é:

void ArvoreBinaria :: PosOrdem (No *inicio) {
    if (inicio != NULL) {
        this->PosOrdem (inicio->esquerdo);
        this->PosOrdem (inicio->direito);
        cout << inicio->valor << " ";
    }
}

O algoritmo recursivo desse percurso em Java é:

public void posOrdem(No no) {
    if (no != null) {
        posOrdem(no.filhoEsquerdo);
        posOrdem(no.filhoDireito);
        System.out.println(no.valor);
    }
}

Para a árvore acima, o percurso seria: 2, 5, 11, 6, 7, 4, 9, 5 e 2. Veja a linha de execução:

• posOrdem(2→esq)
  • posOrdem(7→esq)
    • posOrdem(2→esq)
    • posOrdem(2→dir)
    • visita(2)
  • posOrdem(7→dir)
    • posOrdem(6→esq)
      • posOrdem(5→esq)
      • posOrdem(5→dir)
      • visita(5)
    • posOrdem(6→dir)
      • posOrdem(11→esq)
      • posOrdem(11→dir)
      • visita(11)
    • visita(6)
  • visita(7)
• posOrdem(2→dir)
  • posOrdem(5→esq)
  • posOrdem(5→dir)
    • posOrdem(9→esq)
      • posOrdem(4→esq)
      • posOrdem(4→dir)
      • visita(4)
    • posOrdem(9→dir)
    • visita(9)
  • visita(5)
• visita(2)

Em-nível

O percurso em nível de uma árvore binária consiste em realizar operações em todos os nós, um nível por vez. Para que isso seja possível é necessária a utilização de outra estrutura de dados, sendo ela a fila. Sabendo disso, pode-se utilizar o seguinte pseudo-algoritmo para realizar o percurso em nível de uma árvore:

inicia em_nivel

    instanciar fila;

    fila = no_raiz

    inicia_enquanto (tamnho_da_fila != 0)
        elemento_retirado = retira_elemento_da_fila;
    
        realizar_processo_desejado;
    
        se (filho_esquerda != null)
            fila = filho_esquerda;
        if (filho_direita != null)
            fila = filho_direita;
    finaliza_enquanto
    
finaliza em_nivel;

Contagem dos nós

Uma árvore binária que tenha todas as suas folhas completas possui o número de nós $(N)$, em relação ao total de níveis da árvore $(n)$, dado pela seguinte expressão:

${\text{Nº de nós }}(N)=2^{n}-1$

Exemplos a partir de programação

Em Java

public int contagem(No no){
    return (no == null) ? 0 : 1 + contagem(no.filhoEsquerdo) + contagem(no.filhoDireito);
}

Em C

 int contagem(struct node *tree) {
    return (tree != NULL) ? (contagem(tree->left) + contagem(tree->right) + 1) : 0;
 }

Transformação de uma árvore n-ária

Usar uma matriz para representar uma árvore n-ária é ineficiente, porque a maioria dos nódulos em aplicações práticas contêm menos de n filhos. Como resultado, este fato leva a uma matriz esparsa com grande espaço não utilizado na memória. Converter uma árvore n-ária arbitrária em uma árvore binária só aumentaria a altura da árvore por um fator constante e não afetaria a complexidade geral do pior dos casos. Em outras palavras, $O(\log _{m}n)\equiv O(\log _{2}n)$ visto que $\log _{2}m\cdot \log _{m}n={\frac {\log m}{\log 2}}\cdot {\frac {\log n}{\log m}}=\log _{2}n$.

Primeiro, vinculamos todos os nós dos filhos imediatos de um determinado nó dos pais, para assim formar uma lista de links. Em seguida, mantemos o vínculo do pai com o primeiro (ou seja, o filho mais à esquerda) e removemos todos os outros links para o resto dos filhos. Repetimos esse processo para todos os filhos (caso possua) até que tenhamos processado todos os nós internos, e depois giramos a árvore em 45 graus no sentido horário. A árvore obtida é a árvore binária desejada obtida da árvore n-ária dada.

Uma árvore n-ária qualquer (árvore cujos nós possuem graus menores ou iguais a n) podem ser representados por uma árvore binária. Um exemplo dessa transformação pode ser vista na imagem abaixo:

Um exemplo de conversão de uma árvore n-ária para uma árvore binária.

Métodos para representação de árvores binárias

Uma das maneiras mais simples de representar árvores binárias em linguagens de programação é por meio de arranjos unidimensionais (vetores). Caso a raiz esteja na posição zero, dado um nó de índice i qualquer, os seus filhos terão índices $2i+1$ e $2i+2$ e o seu pai terá índice piso((i - 1)/2). Caso a raiz esteja na posição um, os filhos terão índices $2i$ e $2i+1$ e o pai terá índice piso(i/2). Essa implementação é utilizada para representar árvores completas ou quase completas. Heaps, que são árvores binárias quase completas são implementadas na forma de um vetor de uma maneira bastante eficiente.

Apesar da simplicidade, essa representação requer uma grande quantidade de memória contígua para o armazenamento de árvores grandes, o crescimento desta é díficil de implementar e manter e pode haver grande quantidade de desperdício de memória.

Uma pequena árvore binária com raiz na posição 0, representada como um vetor.

Em uma linguagem que possua suporte a estruturas e referências (por exemplo pascal e C), as árvores podem ser implementadas a partir de nós, com um, ou mais, campos para a(s) informação(ões) principal(is) e dois campos apontadores especiais, denominados esquerda e direita, que fazem referência às subárvores esquerda e direita, respectivamente. Algumas vezes, há um apontador para o pai. Em um nó do tipo folha, os campos apontadores possuem valores especiais (nil em Pascal e "NULL" em C).

Ver também

• Árvore AVL
• Árvore B
• Árvore B+
• Árvore binária de busca
• Árvore binária com costura