Diagrama de Hasse

Elementos de P( P( P(P({})))) em Diagrama de Hasse.

Em teoria da ordem, um ramo da matemática que estuda várias clases de relações binárias, um diagrama de Hasse (alemão: /ˈhasə/) é um tipo de diagrama matemático utilizado para representar um conjunto parcialmente ordenado finito, na forma de um grafo de sua redução transitiva. A redução transitiva de uma relação binária $R$ em um conjunto X é a relação mínima $R'$ em X tal que o fecho transitivo de $R'$ é o mesmo que o fecho transitivo de $R$.

Diagramas de Hasse foram assim denominados em referência a Helmut Hasse (1898–1979); de acordo com Birkhoff (1948), eles são assim chamados por causa do uso efetivo que Hasse fez deles. Entretanto, Hasse não foi o primeiro a utilizar estes diagramas; eles apareceram, e.g., em Vogt (1895). Embora os diagramas de Hasse tenham sido criados inicialmente para possibilitar o desenho à mão de conjuntos parcialmente ordenados, recentemente foram feitos automaticamente utilizando técnicas para desenho de grafos.

A expressão "Diagrama de Hasse" pode também se referir à redução transitiva como um grafo orientado acíclico abstrato, independentemente de qualquer desenho do grafo, mas este uso é evitado aqui.

Definição

Dois membros x e y de um conjunto parcialmente ordenado (S, ≤) são tais que «y cobre x» se x ≤ y e não há z tal que x ≤ z ≤ y. Para um conjunto parcialmente ordenado (S, ≤), um diagrama de Hasse é um grafo onde:

• Cada vértice representa cada elemento de S;
• Cada aresta sobe de x até y sempre que «y cobre x»;

Estas curvas podem se cruzar, mas não devem tocar outros vértices além daqueles que está ligando. Tal diagrama, com vértices nomeados, determina unicamente esta ordem parcial.

Exemplos

• O conjunto potência de { x, y, z } parcialmente ordenado por inclusão, tem o diagrama de Hasse:

• O conjunto A = { 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60 } de todos os divisores de 60, parcialmente ordenado por divisibilidade, tem o diagrama de Hasse:

Um bom diagrama de Hasse

Embora diagramas de Hasse sejam ferramentas simples e intuitivas para lidar com posets finitos, desenhar bons diagramas de Hasse se mostra uma tarefa dificil. O motivo é que em geral existirão muitas maneiras possíveis para se desenhar um diagrama de Hasse para um dado poset. A simples técnica de começar com os elementos minimais de uma ordem e então adicionar elementos maiores incrementalmente frequentemente produz resultados pobres: simetrias e estruturas internas da ordenação são facilmente perdidas.

Subconjuntos

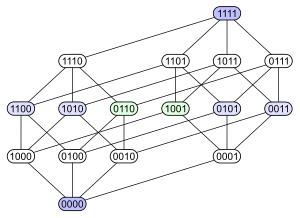
O exemplo seguinte mostra o problema. Considere o conjunto das partes ${\mathcal {P}}(S)$ do conjunto S = {a, b, c, d}, i.e. o conjunto de todos os subconjuntos de S, ordenado pela relação de inclusão $\subseteq$. Abaixo estão três diagramas de Hasse diferentes para esta ordem parcial (Note que cada subconjunto S’ tem o vértice nomeado com uma codificação 1-0 de para cada um dos quatro elementos, sendo ('1') se está ou ('0') se não está presente em S’.):

O diagrama mais a esquerda deixa claro que o conjunto das partes é um poset graduado. O diagrama do meio tem a mesma estrutura graduada, mas ao fazer algumas arestas maiores do que outras ele dá enfase na construção do conjunto das partes como a união de dois cubos tridimensionais: os vértices do cubo abaixo (esquerda) representam subconjuntos que não contém um elemento particular (digamos d) de S, enquanto que o de cima (direita) representa os subconjuntos que contém d. O diagrama mais a direita mostra algumas das simetrias internas da estrutura.

Partições

O diagrama de Hasse seguinte também mostra as partições de um conjunto com quatro elementos, ordenados pela relação de refinamento. O diagrama da esquerda enfatiza o fato dos elementos 0...4 formarem uma reticulado. Todo o reticulado não é simplesmente um semirreticulado dobrado como no exemplo do hipercubo acima. O segundo diagrama é simétrico refletido. As arestas no meio seriam todas verticais, mas para torná-las discrimináveis elas estão desenhadas levemente curvadas. O terceiro diagrama enfatiza a estrutura graduada do reticulado. Todos os elementos com o mesmo rank estão no mesmo nível do diagrama de Hasse, mas muito da simetria está perdida.

Planaridade para cima

Este diagrama de Hasse reticulado de subgrupos de um Grupo diedral Dih₄ não possui arestas que se cruzam.

Se uma ordem parcial pode ser desenhada em um diagrama de Hasse sem que haja duas arestas que se cruzem, este grafo de cobertura é dita ser um grafo planar. Um número de resultados sobre um diagrama de Hasse planar para cima e livre de cruzamentos são conhecidos:

• Se a ordem parcial a ser desenhada é um reticulado, então ela pode ser desenhada sem cruzamentos de arestas se e somente se a dimensão da ordem for no máximo dois. Neste caso, um desenho sem cruzamentos pode ser encontrado derivando-se as Coordenadas Cartesianas dos elementos a partir de suas posições, e então rotacionando o desenho no sentido contrário ao do relógio um ângulo de 45 graus.
• Se a ordem parcial tem no máximo um elemento minimal, ou no máximo um elemento máximal, então pode ser verificado em tempo linear se ela tem um diagrama de Hasse sem cruzamentos.
• É um problema NP-completo determinar se uma ordem parcial com multiplos elementos minimais e maximais pode ser desenhado em um diagrama de Hasse sem cruzamento de arestas. Entretanto, achar um cruzamento em um diagrama de Hasse é tratável com parâmetro fixo quando parametrizado pelo número de pontos de articulaçãoe componentes triconectados da redução transitiva da ordem parcial.
• Se as coordenadas y dos elementos de uma ordem parcial são especificados, então um diagrama de Hasse livre de cruzamentos com respeito a estas atribuições pode ser encontrado em tempo linear, se tal diagrama existir. Em particular, se o poset é graduado, é possível determinar em tempo linear quando existe um diagrama de Hasse livre de cruzamentos no qual o peso de cada vértice é proporcional a seu rank.

Notas

• Este artigo foi inicialmente traduzido, total ou parcialmente, do artigo da Wikipédia em inglês cujo título é «Hasse diagram», especificamente desta versão.

Referências

• Baker, K. A.; Fishburn, P.; Roberts, F. S. (1971), «Partial orders of dimension 2», Networks, 2 (1): 11–28, doi:10.1002/net.3230020103 
• Bertolazzi, R; Di Battista, G.; Mannino, C.; Tamassia, R. (1993), «Optimal upward planarity testing of single-source digraphs», Proc. 1st European Symposium on Algorithms (ESA '93), Lecture Notes in Computer Science, 726, Springer-Verlag, pp. 37–48, doi:10.1007/3-540-57273-2_42 
• Birkhoff, Garrett (1948), Lattice Theory Revised ed. , American Mathematical Society 
• Chan, Hubert (2004), «A parameterized algorithm for upward planarity testing», Proc. 12th European Symposium on Algorithms (ESA '04) 🔗, Lecture Notes in Computer Science, 3221, Springer-Verlag, pp. 157–168 
• Di Battista, G.; Tamassia, R. (1988), «Algorithms for plane representation of acyclic digraphs», Theoretical Computer Science, 61: 175–178, doi:10.1016/0304-3975(88)90123-5 
• Freese, Ralph (2004), «Automated lattice drawing», Concept Lattices, Lecture Notes in Computer Science, 2961, Springer-Verlag, pp. 589–590 . An extended preprint is available online: [1]
• Garg, Ashim; Tamassia, Roberto (1995a), «Upward planarity testing», Order, 12 (2): 109–133, doi:10.1007/BF01108622 
• Garg, Ashim; Tamassia, Roberto (1995b), «On the computational complexity of upward and rectilinear planarity testing», Graph Drawing (Proc. GD '94), LectureNotes in Computer Science, 894, Springer-Verlag, pp. 286–297, doi:10.1007/3-540-58950-3_384 
• Jünger, Michael; Leipert, Sebastian (1999), «Level planar embedding in linear time», Graph Drawing (Proc. GD '99), 1731, pp. 72–81, doi:10.1007/3-540-46648-7_7 
• Vogt, Henri Gustav (1895), Leçons sur la résolution algébrique des équations, Nony, p. 91 

Ligações externas

• Weisstein, Eric W. «Hasse Diagram» (em inglês). MathWorld