Efeito Joule-Thomson

Termodinâmica
Processo de convecção.
Glossário de termodinâmica
Ramos Clássica Estatística Química
Leis Zero Primeira Segunda Terceira
Sistema termodinâmico Sistema termodinâmico Estado Equação de estado Gás ideal Gás real Estados físicos da matéria Equilíbrio Volume de controle Transformações Transformação termodinâmica Isobárica Isocórica Isotérmica Adiabática Isentrópica Isentálpica Politrópica Expansão livre Reversibilidade Irreversibilidade Ciclos Ciclo termodinâmico Máquinas térmicas Ciclo de refrigeração Eficiência termodinâmica
Grandezas físicas Funções de estado Nota: Variáveis conjugadas em itálico Propriedades extensivas e intensivas Calor Calor específico Condutividade térmica Densidade Energia Entropia Fluxo Potência Potencial químico Pressão Temperatura Título Trabalho Vazão Volume
Propriedades Capacidade térmica específica  $c=$ $T$ $\partial S$ $N$ $\partial T$ Compressibilidade  $\beta =-$ $1$ $\partial V$ $V$ $\partial p$ Dilatação térmica  $\alpha =$ $1$ $\partial V$ $V$ $\partial T$
Equações termodinâmicas Teorema de Carnot Lei dos gases ideais Relações de Maxwell Teorema da equipartição Teorema do virial Lei de Henry Lei de Boyle-Mariotte Equação de Van der Waals Raio de Van der Waals Lei de Charles
Potencial termodinâmico Potencial termodinâmico Energia livre Energia interna $U(S,V)$ Entalpia $H(S,p)=U+pV$ Energia livre de Helmholtz $A(T,V)=U-TS$ Energia livre de Gibbs $G(T,p)=H-TS$
História Cultura História Geral Leis dos gases Filosofia Demônio de Maxwell Teorias Teoria calórica Teoria do calor Vis viva ("força viva") Equivalente mecânico do calor Potência motriz
Cientistas Bernoulli Boltzmann Carnot Clapeyron Clausius Carathéodory Duhem Gibbs von Helmholtz Joule Maxwell von Mayer Onsager Rankine Smeaton Stahl Thompson Thomson van der Waals Waterston

Em termodinâmica, o efeito Joule-Thomson ou efeito Joule-Kelvin ou efeito Kelvin-Joule descreve a variação da temperatura de um gás ou líquido quando ele é forçado a passar através de uma válvula ou tampão poroso, enquanto mantido isolado, de modo que nenhum calor seja trocado com o ambiente. Este procedimento é chamado de processo de estrangulamento ou válvula Joule-Thomson. À temperatura ambiente, todos os gases, exceto hidrogênio, hélio e neônio, resfriam-se sob a expansão do experimento de Joule-Thomson.

O efeito tem esse nome em homenagem a James Prescott Joule e William Thomson, o 1º Barão Kelvin, que descobriram-no em 1852, na sequência de trabalhos anteriores de Joule sobre a expansão de Joule, em que um gás sofre expansão livre no vácuo.

Descrição

A expansão adiabática (sem troca de calor) de um gás pode ser realizada de várias maneiras. A mudança de temperatura experimentada pelo gás durante a expansão depende não só das pressões inicial e final, mas também da maneira como a expansão é realizada.

• Se o processo de expansão é reversível, o que significa que o gás está em equilíbrio termodinâmico em todos os instantes, ela é chamada expansão isentrópica. Neste cenário, o gás realiza trabalho positivo durante a expansão, e sua temperatura diminui.
• Em uma expansão livre, por outro lado, o gás não realiza trabalho e não absorve calor, assim a energia interna é conservada. Expandido livremente, a temperatura de um gás ideal deveria permanecer constante, mas a temperatura de um gás real pode aumentar ou diminuir, dependendo da temperatura e pressão iniciais.
• O método de expansão discutido neste artigo, no qual um gás ou líquido a uma pressão P1 flui para uma região à baixa pressão P2 através de uma válvula ou tampão poroso, sob condições estáveis e sem variação na energia cinética, é chamada de experimento de Joule-Thomson . Durante este processo, a entalpia permanece inalterada (veja a demostração abaixo).

O processo de estrangulamento ocorre ao longo de uma curva à entalpia constante, no sentido em que a pressão diminui, o que significa que o processo ocorre da esquerda para a direita em um diagrama T-P. À medida que avançamos ao longo de uma curva de entalpia constante, a altas pressões, a temperatura aumenta, até a temperatura de inversão. Então, como o líquido continua a se expandir, a temperatura cai. Se fizermos isso para várias curvas de entalpia constante e juntarmos os pontos de inversão, uma curva chamada de curva de inversão é obtida. Esta curva intercepta o eixo T em alguma temperatura, chamada de temperatura de inversão máxima. Para o hidrogênio, a temperatura é -68°. Na refrigeração por compressão de vapor, é preciso regular a pressão do gás e resfriá-lo ao mesmo tempo. Isto representa uma barreira para as substâncias cuja temperatura de inversão máxima está bem abaixo da temperatura ambiente. Assim, o hidrogênio precisa ser resfriado abaixo de sua temperatura de inversão se o resfriamento é obtido através do estrangulamento.

O mecanismo físico

Uma vez que o gás se expande, a distância média entre as moléculas aumenta. Devido às forças atrativas intermoleculares (ver força de van der Waals), a expansão produz um aumento na energia potencial do gás. Se nenhum trabalho externo é extraído no processo e nenhum calor é transferido, a energia total do gás permanece a mesma por causa da conservação da energia. O aumento da energia potencial, portanto, implica numa diminuição da energia cinética e portanto uma diminuição de temperatura.

Um segundo mecanismo tem o efeito oposto. Durante as colisões com as moléculas do gás, a energia cinética é temporariamente convertida em energia potencial. Como a distância média intermolecular aumenta, há uma queda no número de colisões por unidade de tempo, o que provoca uma diminuição da energia potencial média. Mais uma vez, a energia total é conservada, então isto leva a um aumento na energia cinética (temperatura). Abaixo da temperatura de inversão de Joule-Thomson, o efeito anterior (o trabalho interno realizado contra as forças atrativas intermoleculares) predomina, e a expansão livre provoca uma diminuição na temperatura. Acima da temperatura de inversão, as moléculas de gás se movem mais rapidamente e assim colidem com mais freqüência, e o último efeito (colisões reduzidas produzindo diminuição na energia potencial média) predomina: a expansão de Joule-Thomson provoca um aumento da temperatura.

O coeficiente de Joule-Thomson

Coeficientes de Joule-Thomson para vários gases à pressão atmosférica.

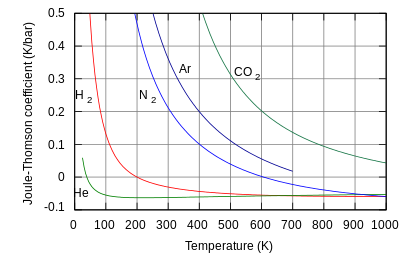
A taxa de variação da temperatura T em relação à pressão P em um processo de Joule-Thomson (isto é, à entalpia constante H) é o coeficiente de Joule-Thomson $\mu _{\mathrm {JT} }$. Este coeficiente pode ser expresso em termos do volume molar V do gás, da sua capacidade térmica à pressão constante $C_{\mathrm {p} }$ e de seu coeficiente de expansão térmica $\alpha$ como:

$\mu _{\mathrm {JT} }\equiv \left({\partial T \over \partial P}\right)_{H}={\frac {V}{C_{\mathrm {p} }}}\left(\alpha T-1\right)\,$

Veja a dedução do coeficiente de Joule-Thomson (Kelvin) abaixo, para a demonstração desta relação. O valor de $\mu _{\mathrm {JT} }$ é normalmente expresso em °C/bar (SI units: K/Pa) e depende do tipo de gás, da temperatura e da pressão do gás antes da expansão. A sua dependência com a pressão normalmente é apenas uma pequena percentagem para pressões até 100 bar.

Todos os gases reais têm um ponto de inversão no qual o valor de $\mu _{\mathrm {JT} }$ muda de sinal. A temperatura ndeste ponto, a temperatura de inversão de Joule-Thomson, depende da pressão do gás antes da expansão.

Numa expansão a pressão diminui, assim o sinal de $\partial P$ é negativo por definição. Com isso em mente, a tabela a seguir mostra quando o efeito Joule-Thomson resfria ou aquece um gás real:

Se a temperatura do gás está	então $\mu _{\mathrm {JT} }$ é	desde que $\partial P$ é	assim $\partial T$ deve ser	logo o gás
abaixo da temperatura de inversão	positivo	sempre negativo	negativo	é resfriado
acima da temperatura de inversão	negativo	sempre negativo	positivo	é aquecido

Hélio e hidrogênio são dois gases cujas temperaturas de inversão de Joule-Thomson a uma pressão de 1 atm são muito baixas (por exemplo, cerca de 51 K (-222 °C) para o hélio). Assim, o hélio e o hidrogênio aquecem-se quando expandem-se à entalpia constante à temperatura ambiente típica. Por outro lado, o nitrogênio e o oxigênio, os dois gases mais abundantes na atmosfera, têm temperaturas inversão de 621 K (348 °C) e 764 K (491 °C), respectivamente: estes gases podem ser resfriados à temperatura ambiente pelo efeito Joule-Thomson.

Para um gás ideal, $\mu _{\mathrm {JT} }$ é sempre igual a zero: gases ideais nem se aquecem nem se resfriam ao serem expandidos à entalpia constante.

Aplicações

Na prática, o efeito Joule-Thomson é realizado permitindo-se que o gás se expanda através de um dispositivo de estrangulamento (normalmente uma válvula), que deve estar muito bem isolado para impedir qualquer transferência de calor para ou pelo gás. Nenhum trabalho externo é extraído do gás durante a expansão (o gás não deve ser expandido através de uma turbina, por exemplo).

O efeito é aplicado com a técnica de Linde como um processo padrão na indústria petroquímica, onde a refrigeração é utilizada para liquefazer gases, e também em várias aplicações criogênicas (por exemplo, para a produção de oxigênio, nitrogênio, e argônio líquidos). Apenas quando o coeficiente de Joule-Thomson para o gás na determinada temperatura é maior que zero o gás pode ser liquefeito a essa temperatura pelo ciclo de Linde. Em outras palavras, um gás deve estar abaixo da sua temperatura de inversão para ser liquefeito pelo ciclo de Linde. Por esta razão, o ciclo de Linde simples normalmente não pode ser utilizado para liquefazer hélio, hidrogênio e neônio.

Demonstração de que a entalpia permanece constante em um processo de Joule-Thomson

Em um processo de Joule-Thomson a entalpia permanece constante. Para demonstrar isso, o primeiro passo é calcular o trabalho líquido realizado pelo gás que se move através da válvula. Suponha que o gás tem um volume V₁ na região à pressão P₁ (região 1) e um volume V₂ quando ele chega à região à pressão P₂ (região 2). Então o trabalho realizado sobre o gás pela fração de gás na região 1 é P₁V₁. Na região 2, o trabalho realizado pelo gás é P₂V₂. Assim, o trabalho total realizado pelo gás é

$P_{2}V_{2}-P_{1}V_{1}\,$

A variação na energia interna mais o trabalho realizado pelo gás é, pela primeira lei da termodinâmica, a quantidade total de calor absorvido pelo gás (aqui supõe-se que não há variação na energia cinética). No processo de Joule-Thomson, o gás é mantido isolado, de forma que nenhum calor é absorvido. Isso significa que

$U_{2}-U_{1}+P_{2}V_{2}-P_{1}V_{1}=0\,$

onde $U_{1}$ e $U_{2}$ denotam a energia interna do gás nas regiões 1 e 2, respectivamente.

Utilizando a definição de entalpia $H=U+PV$, a equação acima implica que:

$H_{1}=H_{2}\,$

onde $H_{1}$ e $H_{2}$ denotam a entalpia do gás nas regiões 1 e 2, respectivamente.

Dedução do coeficiente de Joule–Thomson

É uma dedução da expressão

$\mu _{\mathrm {JT} }\equiv \left({\frac {\partial T}{\partial P}}\right)_{H}={\frac {V}{C_{\mathrm {p} }}}\left(\alpha T-1\right)\,$

para o coeficiente de Joule–Thomson.

A derivada parcial de T em relação a P a H constante pode ser calculada expressando-se a entalpia diferencial dH em termos de dT e dP, e igualando-se a expressão resultante a zero e resolvendo-se para a razão entre dT e dP.

Segue da relação termodinâmica fundamental que a diferencial da entalpia e dada por:

$dH=TdS+VdP\,$ (aqui $S$ é a entropia do gás).

Expressando dS em termos de dT e dP, temos:

$dH=T\left({\frac {\partial S}{\partial T}}\right)_{P}dT+\left[V+T\left({\frac {\partial S}{\partial P}}\right)_{T}\right]dP\,$

Usando

$C_{\mathrm {p} }=T\left({\frac {\partial S}{\partial T}}\right)_{P}\,$ (ver Calor específico), podemos escrever:

$dH=C_{\mathrm {p} }dT+\left[V+T\left({\frac {\partial S}{\partial P}}\right)_{T}\right]dP\,$

A derivada parcial de S restante pode ser expressa em termos do coeficiente de expansão térmica através de uma relação de Maxwell, como se segue. A partir da relação termodinâmica fundamental, segue-se que a diferencial da energia de Gibbs é dada por:

$dG=-SdT+VdP\,$

A simetria entre as derivadas parciais de G em relação a T e P implica que:

$\left({\frac {\partial S}{\partial P}}\right)_{T}=-\left({\frac {\partial V}{\partial T}}\right)_{P}=-V\alpha \,$

onde $\alpha$ é o coeficiente de expansão térmica. Usando esta relação, a diferencial de H pode ser expressa como

$dH=C_{\mathrm {p} }dT+V\left(1-T\alpha \right)dP\,$

Igualando dH a zero e resolvendo para dT/dP, obtemos finalmente:

$\left({\frac {\partial T}{\partial P}}\right)_{H}={\frac {V}{C_{\mathrm {p} }}}\left(\alpha T-1\right)\,$

É fácil verificar que para um gás ideal o coeficiente de expansão térmica $\alpha$ é $1/T$, e assim um gás ideal não sente o efeito Joule-Thomson. O resfriamento de um gás por uma expansão isentrópica pura não é o resfriamento de Joule-Thomson, embora isso seja às vezes erroneamente chamado de resfriamento Joule-Thomson por alguns profissionais experimentais.

Ver também

• Temperatura crítica
• Gás ideal
• Entalpia
• Refrigeração
• Processo reversível

Referências

• Este artigo foi inicialmente traduzido, total ou parcialmente, do artigo da Wikipédia em inglês cujo título é «Joule-Thomson effect», especificamente desta versão.

Bibliografia

• M. W. Zemansky (1968). Heat and Thermodynamics; An Intermediate Textbook. [S.l.]: McGraw-Hill. pp. 182, 355.  
• D. V. Schroeder (2000). An Introduction to Thermal Physics. [S.l.]: Addison Wesley Longman. p. 142. ISBN 0-201-38027-7 
• C. Kittel, H. Kroemer (1980). Thermal Physics. [S.l.]: W. H. Freeman. ISBN 0-7167-1088-9 

Ligações externas

• Joule–Thomson processfrom Eric Weisstein's World of Physics
• Joule–Thomson coefficientfrom Eric Weisstein's World of Physics
• Joule–Thomson effectfrom the truncated free online version of the Encyclopædia Britannica.
• Inversion Curve of Joule-Thomson Effect using Peng-Robinson CEOSfrom Demonstrations Projects of Wolfram Mathematica.