Função de Heaviside

Gráfico da função de Heaviside

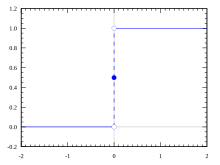
Em matemática e estatística, a função de Heaviside (função degrau) é a função descontínua de valor zero para argumento negativo, e um para argumento positivo. Para argumento nulo sua imagem, situada no intervalo aberto (0;1) não é importante, porque normalmente a função é usada como uma distribuição, mas costuma-se definir:

$H(x) = \frac{1+\sgn(x)}{2} = \begin{cases} 0, & x < 0 \\ \frac{1}{2}, & x = 0 \\ 1, & x > 0 \end{cases} \;\;\;\;\; (1)$

sendo sgn a função sinal.

Aproximações contínuas para a função de Heaviside

A expressão (1) define H(x) como uma função descontínua. Em algumas aplicações, é útil partir de funções contínuas adequadas e definir H(x) como um limite. Por exemplo:

$H(x) \;=\; \lim_{\epsilon \to 0} \left[ \frac{1}{2} \;+\; \frac{1}{\pi} \; arctan \left( \frac{x}{\epsilon}\right) \right] \;\;\;\;\; (2a)$

$H(x) \;=\; \lim_{\epsilon \to 0} \; \frac{1}{2} \; erfc \left( \frac{x}{\epsilon}\right) \;\;\;\;\; (2b)$

$H(x) \;=\; \lim_{\epsilon \to 0} \left[ \frac{1}{2} \;+\; \frac{1}{\pi} \; Si \left( \frac{\pi x}{\epsilon}\right) \right] \;\;\;\;\; (2c)$

$H(x) \;=\; \lim_{\epsilon \to 0} \int_{-\infty}^{x} \frac{1}{\epsilon} \; rect \left( \frac{u}{\epsilon}\right) du \;\;\;\;\; (2d)$

$H(x) \;=\; \lim_{\epsilon \to 0} \int_{-\infty}^{x} \frac{1}{\epsilon} \; tri \left( \frac{u}{\epsilon} \;-\; \frac{1}{2} \right) du \;\;\;\;\; (2e)$

$H(x) \;=\; \lim_{\epsilon \to 0+} \left[ 1 \;-\; e^{- \left( \frac{x}{\epsilon} \right)} \right] \;\;\;\;\; (2f)$

onde erfc(x) é a função erro complementar = 1 - erf(x), Si é a função seno integral, rect é a função retangular e tri(x) é a função triangular .

Relação com outras funções

Função sinal

A expressão (1) deixa clara a relação algébrica entre H(x) e sgn(x). Podemos escrever também:

$sgn(x) \;=\; 2H(x) \;-\; 1 \;\;\;\;\; (3a)$

Delta de Dirac

A distribuição (ou função generalizada) Delta de Dirac δ(x) pode ser vista informalmente como a derivada da função de passo de Heaviside:

$H(x) = \int_{-\infty}{x} \delta(u) \; du \;\;\;\;\; (3b)$

$\delta(x) = \frac{d}{dx} \; H(x) \;\;\;\;\; (3c)$

Mais formalmente, pode-se escrever (3c) da seguinte maneira:

$\delta(x) = \lim_{\epsilon \to 0} \; \frac{d}{dx} \; H(\epsilon,x)$

com H(ε,x) dada por alguma das expressões (2a) a (2f), que são diferenciáveis em x = 0 .

Função retangular

A função retangular pode ser escrita como:

$rect(x) \;=\; H \left( x \;+\; \frac{1}{2} \right) \;-\; H \left( x \;-\; \frac{1}{2} \right) \;\;\;\;\; (3d)$

Este artigo sobre matemática é mínimo. Você pode ajudar a Wikipédia expandindo-o.