História da criptografia
A história da criptografia começa há milhares de anos. Até décadas recentes, ela havia sido a história do que poderia ser chamado de criptografia clássica — isto é, de métodos de criptografia que usam caneta e papel, ou talvez auxílios mecânicos simples. No começo do século XX, a invenção de complexas máquinas mecânicas e electro-mecânicas, tais como a máquina com rotores Enigma, providenciou meios mais sofisticados e eficientes de encriptação; e a posterior introdução da eletrônica e computação permitiu elaborar esquemas de ainda maior complexidade, muitos completamente inadequáveis ao papel e caneta.
O desenvolvimento da criptografia foi acompanhado pelo desenvolvimento da criptoanálise - a "quebra" de códigos e cifras. A descoberta e aplicação, desde cedo, de análise de frequência para a leitura de comunicações criptografadas, muitas vezes, alterou o curso da história. Portanto, o Telegrama Zimmermann que motivou a entrada dos Estados Unidos na Primeira Guerra Mundial e o fato de que os Aliados conseguiram decifrar as cifras da Alemanha Nazista, encurtou a Segunda Guerra Mundial, em algumas avaliações, em até dois anos.
Até à década de 1970, a criptografia segura foi amplamente utilizada para a proteção de governos. Dois eventos trouxeram-a diretamente para o domínio público: a criação de um padrão de criptografia de chave simétrica (DES), e a invenção da criptografia de chave pública.
Criptografia Geral[editar | editar código-fonte]
Na criptografia, encriptação é o processo de codificação de uma mensagem ou informação, de forma que, somente as pessoas autorizadas conseguem ter acesso. O processo de encriptação não isenta de interferências, mas, evita que o conteúdo possa ser visualizado por qualquer um interceptador. Ela é formada por quatro princípios iniciais, sendo eles: Confidencialidade, autenticação, não repudiabilidade e a integridade da informação, (assim, o remetente não consegue negar o envio da informação).
Dentro da criptografia também ocorre a descriptografia, sendo ela o processo contrário da encriptação, onde somente criadores das plataformas e pessoas com um alto conhecimento na área conseguem efetuar, mesmo assim, é exigido grandes recursos computacionais e conhecimento, além do tempo dedicado a essa atividade ser intenso.
É importante ressaltar que nenhuma forma de criptografia é totalmente segura, Nela podemos citar as:
Assimétricas (Públicas): As chaves são públicas e para cada acesso é gerada uma chave. É mais recomendado utilizar em casos onde irá ser utilizada por diversas pessoas e a localidade de cada usuário é distante.
Simétricas (Privadas): As chaves utilizadas serão idênticas, tanto pelo fornecedor quanto pelor receptor, dessa forma, é melhor ser utilizada para casos em que conseguimos enviar a chave pessoalmente, já que, a partir do momento em que enviamos via web, a mesma pode estar sendo exposta.
Antigamente era muito utilizado por militares e pelo governo como forma de facilitar comunicações secretas, isso tem diminuído com o tempo. Agora, é bem mais comum ser utilizado para a proteção de informações em diversos tipos de sistemas civis.
Hoje em dia, a utilização dessa ferramenta se tornou essencial para quaisquer usuários. Com a evolução das formas de invasões, houve a evolução da criptografia, tendo assim, codificações desde 256 até 1024 bits.
Criptografia nas redes wi-fi[editar | editar código-fonte]
As conexões sem fio, deixam uma grande brecha na segurança, pois pessoas com conhecimentos técnicos conseguem efetuar a interceptação de dados de uma rede.
Desse modo, foram feitas evoluções nas técnicas de criptografia, permitindo assim, uma conexão segura para os usuários, domésticos e também na área empresarial, como resultado, as transações financeiras, dados e informações sigilosas estão mais protegidas.
Criptografia clássica[editar | editar código-fonte]
O primeiro uso conhecido da criptografia foi encontrado em hieróglifos irregulares esculpidos em monumentos do Antigo Império do Egito (a cerca de 4500 anos). [carece de fontes] Porém, não podem ser considerados como tentativas sérias de comunicações secretas, mas sim de ser mensagens misteriosas, intrigas ou mesmo diversão para os alfabetizados.[carece de fontes] Seguem outros exemplos de usos da criptografia, ou algo parecido. Algumas tabuletas de argila na Mesopotâmia, um pouco mais tarde, foram utilizadas para proteger informações, por exemplo, receitas de valor comercial. [carece de fontes] Mais tarde ainda, estudiosos hebreus fizeram uso de simples cifras de substituição monoalfabética (como a cifra Atbash), começando talvez em torno de 500 a 600 a.C. [carece de fontes]

Acredita-se que os gregos antigos conheciam cifras (por exemplo, a cifra de transposição scytale utilizada pelos militares de Esparta).[1] Heródoto fala-nos de mensagens secretas escondidas sob a cera em tabletes de madeira ou como uma tatuagem na cabeça de um escravo oculta pelo cabelo crescido, embora estes não sejam devidamente exemplos de criptografia por si só, já que a mensagem, uma vez conhecida, é de fácil leitura; o que ficou conhecido como esteganografia. Outro método grego foi desenvolvido por Políbio (agora chamado de "Quadrado de Políbio").[1] Os romanos conheciam um pouco de criptografia também (por exemplo, a cifra de César e suas variações).
Criptografia medieval[editar | editar código-fonte]

Foi provavelmente por motivos religiosos e através da análise textual do Alcorão que levou à invenção da técnica de análise de freqüência para quebrar cifras de substituição monoalfabética por Alquindi, um matemático árabe, por volta de 800 (Ibraim Alquindi -1992). Foi o avanço mais fundamental da criptoanálise até a Segunda Guerra Mundial. Alquindi escreveu um livro sobre criptografia "Risalah Istikhraj fi al-Mu'amma" ("Manuscrito para decifrar mensagens criptográficas"), no qual ele descreve as primeiras técnicas de criptoanálise, inclusive para cifras polialfabética, classificação de cifra, fonética e sintaxe árabe, e, o mais importante, as primeiras descrições sobre a análise de frequência.[2] Ele também expôs métodos de cifragem, a criptoanálise de certas cifragens, e análise estatística de letras e combinações de letras em árabe.[3][4]
Ahmad al-Qalqashandi (1355–1418) escreveu o Subh al-a 'sha, uma enciclopédia de 14 volumes, que incluía uma seção sobre criptologia. Esta informação foi atribuída a Taj ad-Din Ali ibn ad-Duraihim ben Muhammad ath-Tha 'alibi al-Mausili que viveu de 1312 a 1361, mas cujos trabalhos em criptografia perderam-se. A lista de cifras nesta obra incluía a de substituição e a de transposição, e pela primeira vez, a cifra de múltiplas substituições para cada letra da mensagem de puro-texto. São também atribuídos a Ibn al-Duraihim uma exposição em criptoanálise e um exemplo, incluindo o uso de tabelas de frequência de letras e conjutos de letras que não podem aparecer juntas em uma palavra.
Essencialmente, todas as cifras continuaram vulneráveis a técnica de criptografia de análise de frequência até o desenvolvimento da cifra polialfabética, e muitos permaneceram assim posteriormente. A cifra polialfabética foi melhor explicada por Leon Battista Alberti por volta do ano 1467, por isso ele foi chamado de "pai da criptologia Ocidental".[5] Johannes Trithemius, em sua obra Poligraphia, inventou a tabula recta, uma componente crítica da cifra de Vigenère. O criptógrafo francês Blaise de Vigenère inventou um sistema polialfabético prático que leva seu nome, a cifra de Vigenère.[5]
Na Europa, criptografia tornou-se (secretamente) mais importante como uma consequência da competição política e da revolução religiosa. Por exemplo, na Europa durante e após o Renascimento, cidadãos de vários estados italianos - Estados Pontifícios e a Igreja Católica Romana, inclusive - foram responsáveis pela rápida proliferação de técnicas de criptografia, algumas das quais refletem o entendimento (ou mesmo conhecimento) do progresso polialfabético de Alberti. 'Cifras avançadas', mesmo depois de Alberti, não eram tão avançadas como seus inventores / desenvolvedores / usuários afirmavam(e até acreditavam). Elas foram regularmente quebradas. Este excesso de otimismo pode ser inerente em criptografia para ele era então, e permanece até hoje, fundamentalmente difícil saber com precisão o grau de vulnerabilidade do seu sistema é realmente. Na ausência de conhecimento, as suposições e esperanças, como seria de esperar, são comuns.
Criptografia, criptoanálise, e traição de agente/mensageiro secreto destacaram-se na Conspiração de Babington, durante o reinado da Rainha da Inglaterra Elizabeth I, o que acabou na execução de Maria Stuart, Rainha da Escócia. Uma mensagem cifrada do tempo do Homem da Máscara de Ferro (decifrada logo antes de 1900 por Étienne Bazeries) lançou alguma luz sobre a identidade do prisioneiro, porém, infelizmente, não definitiva.
Fora da Europa, após o fim da Idade de Ouro muçulmano na mão dos mongóis, a criptografia permaneceu relativamente subdesenvolvida. A criptografia no Japão não parece ter sido utilizada até cerca de 1510, e técnicas avançadas não foram conhecidas até após a abertura do país ao Ocidente, no início da década de 1860. Durante a década de 1920, oficiais da Marinha polonesa ajudaram os militares japoneses no desenvolvimento de códigos e cifras.
Criptografia de 1800 a II Guerra Mundial[editar | editar código-fonte]
Embora a criptografia tenha uma história longa e complexa, até o século XIX não foi desenvolvido nada mais do que abordagens ad hoc para a criptografia ou criptoanálise (a ciência de encontrar fragilidades em sistemas de criptografia). Um exemplo é o trabalho de Charles Babbage, durante a Guerra da Crimeia, em análise matemática de cifras polialfabética, remodelado e publicado pouco depois pelo Prússio Friedrich Kasiski. A criptografia, neste momento, começa a se consolidar com regras consistentes; como, por exemplo, as encontradas nos escritos sobre criptografia de Auguste Kerckhoffs, no final do século XIX e na Constituição Americana passou a ser protegida no século XVIII.[6] Edgar Allan Poe usou métodos sistemáticos para resolver enigmas na década de 1840. Em particular, ele colocou um anúncio de suas habilidades no jornal da Filadélfia Alexander's Weekly (Express) Messenger, solicitando submissões das cifras, das quais ele passou a resolver quase tudo. Seu sucesso criou uma agitação pública por alguns meses.[7] Mais tarde, ele escreveu um ensaio sobre os métodos de criptografia, que tornou-se útil como uma introdução para os criptoanalistas britânicos na quebra dos códigos e cifras alemãs durante a I Guerra Mundial, e uma história famosa, O Escaravelho de Ouro, onde a criptoanálise era um elemento de destaque.
Criptografia, e seu uso incorreto, estiveram envolvidos na conspiração que levou à execução de Mata Hari e na conivência que levou à farsa da condenação e prisão de Dreyfus, no início do século XX. Felizmente, criptógrafos também estavam envolvidos em expor as maquinações que originaram os problemas de Dreyfus; Mata Hari, em contrapartida, foi baleada.
Na Primeira Guerra Mundial a Sala 40 do Almirantado quebrou os códigos navais alemães e desempenhou um papel importante em vários combates navais durante a guerra, particularmente na detecção de grandes missões alemãs no Mar do Norte que levou às batalhas de Dogger Bank e Jutlândia, já que a frota britânica foi enviada para interceptá-los. No entanto sua contribuição mais importante provavelmente foi em decodificar o Telegrama Zimmermann, um telegrama do Ministério do Exterior alemão enviado via Washington para o seu embaixador Heinrich von Eckardt] no México, que desempenhou um papel importante na entrada dos Estados Unidos na guerra.
Em 1917, Gilbert Vernam propôs uma cifra de teletipo em que uma chave previamente preparada, mantida em fita de papel, é combinada caractere a caractere com a mensagem de puro-texto para produzir o texto cifrado. Isto levou ao desenvolvimento de dispositivos eletromecânicos como máquinas de cifra.
Métodos matemáticos foram desenvolvidos no período anterior à Segunda Guerra Mundial (particularmente na aplicação de técnicas estatísticas para criptoanálise e desenvolvimento de cifras de William F. Friedman e na ruptura inicial da versão do Enigma do Exército Alemão por Marian Rejewski) em 1932.
Criptografia na II Guerra Mundial[editar | editar código-fonte]

Até a Segunda Guerra Mundial, as máquinas de codificação mecânica e eletromecânica estavam em uso, embora - onde essas máquinas eram impraticáveis - sistemas manuais ainda eram utilizados. Grandes avanços foram feitos, tanto na concepção de cifras quanto na criptoanálise, tudo em sigilo. Informações sobre esse período começou a ser desclassificado como o período de segredo oficial britânico de 50 anos chegou ao fim, como os arquivos dos EUA abriu lentamente, e como memórias sortidas e artigos foram publicados. Informações sobre esse período começaram a ser desclassificadas assim que o período de segredo oficial britânico de 50 anos chegou ao fim, os arquivos dos EUA serem abertos e as memórias e artigos terem sido publicados.
Os alemães fizeram uso pesado, em várias versões, de um rotor eletromecânico conhecido como Enigma. O matemático Marian Rejewski, no escritório de cifras da Polônia, em dezembro de 1932 deduziu a estrutura detalhada do Enigma do exército alemão, usando matemática e documentação limitada fornecida pelo capitão Gustave Bertrand da inteligência militar francesa. Esse foi o maior avanço na criptoanálise em mais de mil anos, segundo o historiador David Kahn. Rejewski e seus colegas matemáticos do escritório de cifras, Jerzy Rozycki e Henryk Zygalski, continuaram a estudar o Enigma e acompanharam a evolução dos componentes da máquina do exército alemão e seus procedimentos de codificação. Como os recursos dos poloneses tornaram-se escassos devido às alterações introduzidas pelos alemães, e como a guerra se aproximava, o escritório de cifras, sob as instruções do Estado-Maior polonês , em 25 de julho de 1939, em Varsóvia, representantes da inteligência francesa e britânica começaram a trabalhar nos segredos da decodificação do Enigma.
Logo após o estopim da Segunda Guerra Mundial em 1 de setembro de 1939, o pessoal-chave do escritório de cifras foi evacuado em direção ao sudeste, em 17 de setembro, quando a União Soviética atacou a Polônia, eles cruzaram a fronteira com a Romênia. De lá eles chegaram a Paris, França; na estação de inteligência franco-polonesa, PC Bruno, próxima a Paris, eles continuaram quebrando o Enigma, colaborando com criptógrafos britânicos em Bletchley Park, já que os ingleses já tinham agilidade na quebra do Enigma. Na devida altura, os criptógrafos britânicos (muitos deles mestres de xadrez e matemáticos, tais como William Gordon Welchman, Max Newman e Alan Turing, fundador conceitual da computação moderna) fizeram um progresso substancial na tecnologia de decodificação do Enigma.
No final da guerra, em 19 de abril de 1945, os oficiais militares superiores da Grã-Bretanha foram informados de que eles nunca poderiam revelar que a cifra Enigma alemã tinha sido quebrada, pois daria ao inimigo derrotado a chance de dizer que "não foram bem e bastante espancados".[8]
Criptógrafos da Marinha dos Estados Unidos (com a colaboração de criptógrafos ingleses e holandeses depois de 1940) invadiram vários sistemas de criptografia da Marinha Japonesa. A quebra de um deles, JN-25, levou à vitória dos EUA na Batalha de Midway; e o fato foi publicado no Chicago Tribune logo após a batalha, embora os japoneses pareciam não ter notado, porque continuaram a usar o sistema JN-25. Um grupo do Exército dos EUA, o SIS(Serviço de Inteligência de Sinais), conseguiu quebrar o mais seguro sistema de codificação diplomática japonês (uma máquina eletromecânica 'telerruptor' chamada pelos americanos de Purple), mesmo antes da Segunda Guerra Mundial começar. Os americanos se referem à inteligência resultante da criptoanálise, talvez especialmente a partir da máquina Purple, como 'Magic'. O que os ingleses chamam de 'Ultra', particularmente a partir de tráfego de mensagens protegidas pelas diversas versões do Enigma. Um termo britânico anterior para Ultra tinha sido 'Boniface', na tentativa de sugerir, se traído, que poderia ter um agente individual como uma fonte.
Os militares alemães também implantaram várias máquinas mecânicas em one-time pad. Bletchley Park chamou as cifras de FISH, e Max Newman e seus colegas projetaram e implantaram o Heath Robinson, o primeiro computador digital eletrônico programável, o Colossus, para ajudar com sua criptoanálise. O Ministério do Exterior alemão começou a usar o one-time pad em 1919; parte do tráfego foi lido na Segunda Guerra Mundial, como resultado da recuperação de uma parte do conjunto de chaves, na América do Sul, que foi descartado displicentemente por um mensageiro alemão.
O Ministério das Relações Exteriores japonês utilizou um sistema desenvolvido localmente baseado no telerruptor elétrico (chamado de Purple pelos EUA), e também tinha usado várias máquinas semelhantes para agregar algumas embaixadas japonesas. Uma delas foi chamada de 'M-machine' pelos EUA, outra máquina era conhecida como 'Red'. Todas foram quebradas, de uma forma ou de outra, pelos Aliados.
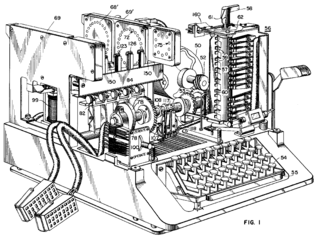
Entre as máquinas de codificação dos Aliados usadas na Segunda Guerra Mundial estão a britânica TypeX e a americana SIGABA; ambas eram rotores eletromecânicos semelhantes ao Enigma, mas com grandes melhorias. Nem uma nem outra foi quebrada durante a guerra. Os poloneses utilizaram a máquina Lacida, mas a sua segurança foi classificada como abaixo do que devia (pelo criptógrafos do Exército Polonês no Reino Unido), e seu uso foi interrompido. As tropas dos EUA no campo usavam o M-209 e ainda, o menos seguro, M-94. Agentes britânicos do SOE usavam inicialmente "cifras poema" (poemas memorizados eram as chaves de encriptação/desencriptação), mas mais tarde durante a Segunda Guerra, eles modificaram para o one-time pad.
A cifra de VIC (usada pelo menos até 1957, associada ao espião Rudolf Abel) foi uma cifra de mão muito complexa, e muitos afirmam ser a cifra mais complicada que foi utilizada pelos soviéticos, de acordo com David Kahn em Kahn on Codes.
Criptografia moderna[editar | editar código-fonte]
O uso da matemática em criptografia e criptoanálise tem avançado desde a Segunda Guerra Mundial. Mesmo assim, só foi possível a utilização eficaz da criptografia para aplicações usuais, através da ampla utilização de computadores e da Internet como um meio de comunicação. Antes a criptografia era utilizada apenas por governos ou grandes empresas.
Shannon[editar | editar código-fonte]
A era da criptografia moderna começa realmente com Claude Shannon, indiscutivelmente o pai da criptografia matemática, com o trabalho que ele fez durante a Segunda Guerra Mundial sobre a segurança das comunicações. Em 1949 ele publicou Communication Theory of Secrecy Systems no Bell System Technical Journal e um pouco mais tarde o livro The Mathematical Theory of Communication, com Warren Weaver.[9] Ambos abordavam os resultados de seu trabalho na Segunda Guerra Mundial. Estes, além de outros trabalhos em teoria da informação estabeleceram uma sólida base teórica para a criptografia e também para grande parte da criptoanálise. E com isso, a criptografia desapareceu em parte das comunicações de organizações secretas do governo como a NSA, GCHQ, e seus equivalentes em outros lugares. Muito pouco trabalho tornou-se público novamente até meados da década de 1970, quando tudo mudou.
Um padrão de criptografia[editar | editar código-fonte]
Em meados da década de 1970 houve dois grandes avanços públicos (ou seja, não-secreto). Primeiro foi a publicação do projeto DES no Registo Federal dos EUA em 17 de março de 1975. A cifra DES proposta foi apresentada por um grupo de pesquisa da IBM, a convite do National Institute of Standards and Technology (agora NIST), em um esforço para desenvolver instalações seguras de comunicações eletrônicas para as empresas, como bancos e outras grandes organizações financeiras. Depois de "conselhos" e modificações introduzidas pelo NSA, agindo nos bastidores, que foi aprovado e publicado como FIPS publicado em 1977 (atualmente em FIPS 46-3). DES foi a primeira cifra publicamente acessível a ser "abençoada" por uma agência nacional, como a NSA. A liberação de sua especificação pelo NBS estimulou uma explosão de interesse público e acadêmico em criptografia.
O antigo DES foi oficialmente substituído pelo AES em 2001, quando NIST anunciou FIPS 197. Depois de um concurso, o NIST selecionou Rijndael, apresentado por dois criptógrafos belga, para ser o AES. DES, e variantes mais seguras dele (como a 3DES), são usadas ainda hoje, tendo sido incorporado em muitos padrões nacionais e organizacionais. No entanto, o seu tamanho de chave de 56 bits tem se mostrado insuficiente para evitar ataques de força bruta (um certo ataque, empreendido pelo grupo de direitos civis EFF, em 1997, conseguiu em 56 horas.[10]). Em conseqüência, o uso da cifra DES é, sem dúvida, inseguro para uso em novos projetos de criptografia, e as mensagens protegidas por sistemas de encriptação mais velhos usando DES, ou seja, as mensagens enviadas a partir de 1976 usando DES, também estão em risco. Independentemente da qualidade intrínseca da cifra DES, o seu tamanho de chave (56 bits) foi considerado muito pequeno por alguns, mesmo em 1976, principalmente por Whitfield Diffie. Havia suspeitas de que organizações governamentais até então tinha poder computacional suficiente para quebrar mensagens DES; claramente outros alcançaram essa capacidade.
Chave pública[editar | editar código-fonte]
O próximo conceito, em 1976, foi talvez ainda mais importante, pois mudou fundamentalmente a forma como sistemas de criptografia funcionam. Surgiu com a publicação do artigo New Directions in Cryptography de Whitfield Diffie e Martin Hellman. Eles introduziram um método radicalmente novo de distribuição de chaves criptográficas, que ia em direção a solução de um dos problemas fundamentais da criptografia, distribuição de chaves, e tornou-se conhecido como Diffie-Hellman. O artigo também estimulou o desenvolvimento público quase que imediato de uma nova classe de algoritmos de cifragem, os algoritmos de chave assimétrica.
Antes disso, todos os algoritmos de cifragem modernos tinham sido algoritmos de chaves simétricas, no qual a mesma chave criptográfica é usada com o algoritmo oculto definido pelo remetente e pelo destinatário, e que deve ser mantido em segredo. Todas as máquinas eletromecânicas utilizadas na Segunda Guerra Mundial foram desta categoria lógica, como foram as cifras de César e a Atbash e essencialmente todos os sistemas de codificação ao longo da história. A "chave" para um código é, naturalmente, o livro de códigos, que também deve ser distribuído e mantido em segredo, assim acontece com a maioria dos problemas na prática.
Por necessidade, a chave em cada sistema, teve que ser trocada entre as partes comunicantes de alguma forma segura antes da utilização do sistema (o termo normalmente usado é 'através de um canal seguro'), como um mensageiro de confiança com uma maleta algemada ao pulso, ou um contato face a face, ou um pombo-correio leal. Esta exigência não é trivial e muito rapidamente se torna incontrolável à medida que o número de participantes aumenta, ou quando os canais seguros não estão disponíveis para a troca de chaves, ou quando, como é prática sensata de criptografia, as chaves são freqüentemente alteradas. Em particular, se as mensagens são destinadas a não serem lidas por outros usuários, uma chave isolada é necessária para cada par possível de usuários. Um sistema deste tipo é conhecido como uma chave secreta ou sistema criptográfico de chave simétrica. O método Diffie-Hellman (e sucessivas melhorias e variantes) faz as operação desses sistemas de modo muito mais fácil e mais seguro, o que nunca foi possível antes em toda a história.
Em contraste, a criptografia de chave assimétrica utiliza um par de chaves matematicamente relacionadas, onde cada uma delas decifra a criptografia usando a outra. Alguns, mas não todos, destes algoritmos têm a propriedade adicional de que uma das chaves do par não pode ser deduzida a partir da outra por qualquer método conhecido, além de tentativa e erro. Um algoritmo deste tipo é conhecido como sistema de chave pública ou sistema de chave assimétrica. Usando esse algoritmo, apenas um par de chaves é necessário por usuário. Ao designar uma das chaves do par como privada (sempre em segredo), e a outra como pública (muitas vezes disponível), nenhum canal seguro é necessário para a troca de chaves. Enquanto a chave privada permanece secreta, a chave pública pode ser conhecida por um tempo muito longo sem comprometer a segurança, tornando-o seguro para reutilizar o mesmo par de chaves indefinidamente.
Para dois usuários de um algoritmo de chave assimétrica se comunicarem de forma segura por um canal inseguro, cada usuário deverá conhecer as suas chaves públicas e privadas, bem como a chave pública do outro usuário. Considere este cenário básico: Alice e Bob têm um par de chaves já utilizadas durante anos com muitos outros usuários. No início da mensagem, eles trocam chaves públicas, não cifradas através de uma linha insegura. Alice, em seguida, cifra uma mensagem usando sua chave privada, e então cifra esse resultado usando a chave pública de Bob. A mensagem duplamente cifrada é então enviada como dados digitais através de um fio de Alice para Bob. Bob recebe o fluxo de bits e decodifica-o usando sua própria chave privada, e depois decodifica o novo fluxo de bits usando a chave pública de Alice. Se o resultado final for reconhecido como uma mensagem, Bob pode estar confiante de que a mensagem veio realmente de alguém que conhece a chave privada de Alice (presumivelmente dela mesma, se ela tem sido cuidadosa com sua chave privada), e de que qualquer abelhudo no canal iria precisar da chave privada de Bob para compreender a mensagem.
Algoritmos assimétricos dependem, para a sua eficiência, de uma classe de problemas de matemática chamada de função unidirecional, que exigem relativamente pouco poder computacional para ser executada, mas muito poder computacional para inverter, se a inversão for possível. Um exemplo clássico de uma função unidirecional é a multiplicação de números primos muito grandes. É bastante rápido determinar o produto de dois primos grandes, mas muito difícil de encontrar os fatores do produto de dois primos grandes. Por causa das funções unidirecionais, a maior parte do conjunto de chaves possíveis são más escolhas para chaves de sistemas de criptografia; apenas uma pequena fração das possíveis chaves de um determinado comprimento é apropriada, e os algoritmos assimétricos exigem chaves muito longas para atingir o mesmo nível de segurança fornecido por chaves simétricas mais curtas. A necessidade de gerar os pares de chaves e executar as operações de codificação e decodificação fazem com que os algoritmos assimétricos tornem-se computacionalmente caros, em comparação com a maioria dos algoritmos simétricos. Uma vez que algoritmos simétricos geralmente podem usar qualquer seqüência de (aleatória, ou pelo menos imprevisível) bits como uma chave, uma chave de sessão disponível pode ser rapidamente gerada para uso a curto prazo. Em consequência, é comum usar uma chave assimétrica longa no lugar de uma chave simética disponível, muito mais curta e também mais forte. O algoritmo assimétrico mais lento envia uma chave de sessão simétrica, e o algoritmo simétrico mais rápido assume o controle para o restante da mensagem.
A criptografia de chave assimétrica, o método Diffie-Hellman, e os mais conhecidos algoritmos de chave pública e privada (isto é, o que normalmente é chamado de algoritmo RSA) possivelmente foram desenvolvidos de forma independente em uma agência de inteligência do Reino Unido antes do anúncio público por Diffie e Hellman em 1976. GCHQ liberou os documentos alegando que eles tinham desenvolvido a criptografia de chave pública antes da publicação do artigo de Diffie e Hellman. Vários artigos confidenciais foram escritos no GCHQ durante os anos 1960 e 1970 que levaram a esquemas essencialmente idênticos ao de criptografia RSA e do método Diffie-Hellman em 1973 e 1974. Alguns destes já foram publicados, e os inventores (James H. Ellis, Clifford Cocks e Malcolm Williamson) tornaram públicos (parte de) seus trabalhos.
Política de criptografia[editar | editar código-fonte]
A evolução do público da década de 1970 quebrou o monopólio sobre a criptografia de alta qualidade realizado por organizações governamentais (ver Crypto de Steven Levy, relato jornalístico de algumas controvérsias políticas da época nos EUA). Pela primeira vez, as organizações de fora do governo tiveram acesso a criptografia de alta qualidade, que não seria quebrada nem mesmo pelo governo. controvérsias e conflitos consideráveis, tanto públicos como privados, surgiram após a quebra do monopólio sobre a criptografia. E ainda continuam. Em muitos países, por exemplo, a exportação de criptografia está sujeita a restrições. Até 1996, exportação de criptografia dos EUA que usava chaves de mais de 40 bits (muito pequena para ser segura contra um invasor experiente) foi severamente limitada. Em 2004, o ex-diretor do FBI, Louis Freeh, testemunhou perante a Comissão do 11 de Setembro, realizada para a definição da nova legislação contra a utilização pública de criptografia.
Uma das pessoas mais significativas a favorecer a criptografia de qualidade para uso público foi Phil Zimmermann. Ele escreveu e, em 1991, lançou o PGP (privacidade bastante boa), um sistema criptográfico de altíssima qualidade. Ele distribuiu uma versão gratuita do PGP, quando se sentiu ameaçado pela legislação do governo dos EUA que exigia a inclusão de Porta dos fundos em todos os produtos de criptografia desenvolvido dentro dos EUA. Seu sistema foi lançado mundialmente logo depois que ele lançou nos EUA, e então iniciou-se uma longa investigação criminal contra ele pelo Departamento de Justiça do Governo dos EUA, pela suposta violação das restrições à exportação. O Departamento de Justiça, posteriormente, retirou o processo contra Zimmermann, e a distribuição gratuita do PGP continuou ao redor do mundo. PGP acabou por se tornar um padrão IETF aberto (RFC 2440 ou OpenPGP).
Criptoanálise moderna[editar | editar código-fonte]
Embora as cifras modernas, como a AES e as cifras assimétricas de altíssima qualidade são amplamente consideradas inquebráveis, projetos e implementações fracos ainda são por vezes adotados e ainda existem quebras de sistemas de criptografia implementados nos últimos anos. Exemplos notáveis de projetos de criptografia quebrados incluem o primeiro esquema de criptografia Wi-Fi, WEP, o Content Scramble System usado para cifrar e controlar o uso de DVD, as cifras A5/1 e A5/2 usadas em telefones celulares GSM, e a cifra CRYPTO1 utilizada amplamente nos cartões inteligentes MIFARE Classic da NXP Semiconductors, uma divisão desmembrada da Philips Electronics. Todas elas são cifras simétricas. Até agora, nenhuma das ideias matemáticas da criptografia de chave pública foram provadas serem "inquebráveis", sendo assim algum avanço na análise matemática pode tornar os sistemas dependente dessas ideias, inseguros. Enquanto alguns observadores bem informados prevêem esse avanço, o tamanho da chave recomendado para a segurança como uma boa prática continua aumentando à medida que a capacidade computacional necessária para quebrar códigos se torna mais barata e disponível.
Referências[editar | editar código-fonte]
- ↑ a b A Short History of Cryptography, Fred Cohen 1995, retrieved 4 February 2011
- ↑ Simon Singh, The Code Book, pp. 14–20
- ↑ «Al-Kindi, Cryptgraphy, Codebreaking and Ciphers». Consultado em 12 de janeiro de 2007
- ↑ Ibrahim A. Al-Kadi (April 1992), "The origins of cryptology: The Arab contributions”, Cryptologia 16 (2): 97–126
- ↑ a b History of Cryptography
- ↑ The Use of Encrypted, Coded and Secret Communications is an "Ancient Liberty" Protected by the United States Constitution
- ↑ Silverman, Kenneth. Edgar A. Poe: Mournful and Never-ending Remembrance. New York: Harper Perennial, 1991. p. 152-3
- ↑ Fenton, Ben (22 de junho de 2006). «Enigma and the British code of honour». The Daily Telegraph. London
- ↑ Shannon, Claude E.; Weaver, Warren (1949). The Mathematical Theory of Communication (em inglês). Illinois: Illini Books. 117 páginas. Library of Congress Catalog Card nº 49-11922
- ↑ Electronic Frontier Foundation, Cracking DES, O'Reilly, 1998.
- David Kahn, The Codebreakers, New York, Macmillan, 1967.
- Steven Levy, Crypto: How the Code Rebels Beat the Government—Saving Privacy in the Digital Age, New York, Viking Press, 2001.
