Testes de hipóteses
| Estatística |
|---|
 |
Teste de hipóteses, teste estatístico ou teste de significância[1] é um procedimento estatístico que permite tomar uma decisão (aceitar ou rejeitar a hipótese nula ) entre duas ou mais hipóteses (hipótese nula ou hipótese alternativa ), utilizando os dados observados de um determinado experimento.[2] Há diversos métodos para realizar o teste de hipóteses, dos quais se destacam o método de Fisher (teste de significância),[3] o método de Neyman–Pearson[4] e o método de Bayes.[5]
Por meio da teoria da probabilidade, é possível inferir sobre quantidades de interesse de uma população a partir de uma amostra observada de um experimento científico. Por exemplo, estimar pontualmente e de forma intervalar um parâmetro de interesse, testar se uma determinada teoria científica deve ser descartada, verificar se um lote de remédios deve ser devolvido por falta de qualidade, entre outros. Por meio do rigor matemático, a inferência estatística pode ser utilizada para auxiliar a tomada de decisões nas mais variadas áreas.[6]
Os testes de hipóteses são utilizados para determinar quais resultados de um estudo científico podem levar à rejeição da hipótese nula a um nível de significância pré–estabelecido. O estudo da teoria das probabilidades e a determinação da estatística de teste correta são fundamentais para a coerência de um teste de hipótese. Se as hipóteses do teste de hipóteses não forem assumidas de maneira correta, o resultado será incorreto e a informação será incoerente com a questão do estudo científico. Os tipos conceituais de erro (erro do tipo I e erro do tipo II) e os limites paramétricos ajudam a distinguir entre a hipótese nula e a hipótese alternativa .[7]
São fundamentais os seguintes conceitos para um teste de hipóteses:[7]
- Hipótese nula (): é a hipótese assumida como verdadeira para a construção do teste. É a teoria, o efeito ou a alternativa que se está interessado em testar.
- Hipótese alternativa (): é considerada quando a hipótese nula não tem evidência estatística.
- Erro do tipo I (): é a probabilidade de se rejeitar a hipótese nula quando ela é verdadeira.
- Erro do tipo II: é a probabilidade de se rejeitar a hipótese alternativa quando ela é verdadeira.
| Hipótese nula é verdadeira | Hipótese nula é falsa | |
|---|---|---|
| Hipótese nula é rejeitada | Erro do tipo I | Não há erro |
| Hipótese nula não é rejeitada | Não há erro | Erro do tipo II |
Origens[editar | editar código-fonte]
O teste de significância é, em grande parte, um produto de Karl Pearson (p–valor e teste qui quadrado de Pearson), William Sealy Gosset (distribuição t de Student) e Ronald Fisher (hipótese nula, análise de variância e teste de significância), enquanto o teste de hipóteses foi desenvolvido por Jerzy Neyman e Egon Pearson (filho do próprio Karl Pearson). Ronald Fisher começou sua vida na estatística na área bayesiana, mas logo se desencantou com a subjetividade envolvida (ou seja, o uso do princípio da indiferença para determinar as probabilidades anteriores) e procurou fornecer uma abordagem mais objetiva da inferência.[8]
Fisher foi um estatístico agrícola que enfatizava o desenho experimental rigoroso e o método para extrair resultado de algumas amostras assumindo as distribuições gaussianas. Neyman enfatizou o rigor matemático e os métodos para obter mais resultados a partir de muitas amostras e uma maior variação de distribuições. Embora os testes de hipóteses modernos tenham sido popularizados no início no século XX, evidências do seu uso podem ser encontradas muito antes. Nos anos 1770, Laplace considerou a estatística de quase meio milhão de nascimentos para mostrar o maior número de meninos em comparação com as meninas.[9] Ele concluiu pelo cálculo do p–valor que o excesso era real, mas inexplicado.[10] Fisher popularizou o teste de significância. Ele exigiu a hipótese nula (correspondente à distribuição da frequência da população) e uma amostra. Seus cálculos determinaram se uma hipótese nula deveria ou não ser rejeitada. O teste de significância não utilizou hipótese alternativa. Então, não havia o conceito erro do tipo II.[11] O p–valor foi concebido como um índice informal (mas objetivo) para ajudar um pesquisador a determinar (com base em outros conhecimentos) se é preciso modificar os experimentos futuros ou fortalecer a crença na hipótese nula.[12]
Os conceitos de "teste de hipóteses", "erro do tipo I" e "erro do tipo II" foram concebidos por Neyman e Pearson como uma alternativa mais objetiva ao p–valor de Fisher para determinar o comportamento do pesquisador sem requerer qualquer inferência indutiva da parte dele.[13][14] Neyman e Pearson consideraram um problema diferente, o qual chamaram de teste de hipóteses. Fisher e Neyman e Pearson entraram em choque. Neyman e Pearson consideravam sua formulação uma generalização melhorada do teste de significância. Entretanto, seu artigo principal On the Problem of the Most Efficient Tests of Statistical Hypotheses era considerado abstrato.[13] Os matemáticos têm generalizado e refinado essa teoria há décadas.[15] Fisher pensou que isso não era aplicável à pesquisa científica porque geralmente, durante o curso do experimento, descobre–se que as afirmações iniciais sobre a hipótese nula são questionáveis devido às fontes inesperadas de erro. Fisher acreditava que o uso de decisões rígidas para rejeição ou aceitação baseada em modelos formulados antes da coleta de dados era incompatível com este cenário comum enfrentado pelos cientistas e as tentativas para aplicar este método à pesquisa científica poderia provocar uma confusão geral.[16] A disputa entre Fisher e Neyman e Pearson foi travada em bases filosóficas, podendo ser caracterizada como uma disputa sobre o papel apropriado dos modelos na inferência estatística.[17]
Neyman aceitou um cargo no Ocidente, rompendo sua parceria com Pearson. A Segunda Guerra Mundial também interrompeu o debate. A disputa entre Fisher e Neyman terminou sem resolução depois de 27 anos com o falecimento de Fisher em 1962. Neyman escreveu um respeitoso elogio ao estatístico.[18] Posteriormente algumas das publicações de Neyman reportaram p–valores e níveis de significância.[19]
Visão moderna[editar | editar código-fonte]
A visão moderna de teste de hipóteses é um híbrido de duas abordagens que resultou da confusão entre autores de livros estatísticos (como previsto por Fisher), começando nos anos 1940.[20] Por exemplo, detecção de sinal ainda usa a formulação de Neyman e Pearson. Grandes diferenças conceituais e muitas advertências, além das mencionadas acima, foram ignoradas. Neyman e Pearson forneceram a terminologia mais forte, a matemática mais rigorosa e a filosofia mais consistente, mas o conteúdo ensinado atualmente em estatística introdutória tem mais similaridades com o método de Fisher que com o método de Neyman e Pearson. Esta história explica a mistura presente da terminologia. Por exemplo, a hipótese nula nunca é aceita, mas pode ser não rejeitada, porém tem uma região de aceitação.[21]
Por volta de 1940, os autores de livros estatísticos começaram a combinar estas duas estratégias anonimamente, usando o p–valor no lugar do teste estatístico para testar contra o nível de significância de Neyman e Pearson.[20] Portanto, os pesquisadores eram encorajados a inferir a força dos seus dados contra algumas hipóteses nulas, usando p–valores, enquanto eles também pensavam que estavam mantendo a objetividade pós coleta de dados fornecida pelo teste de hipóteses. Em seguida, isto se tornou usual para a hipótese nula, que era originalmente uma hipótese de pesquisa realista, que seria usada quase que exclusivamente como a hipótese para a qual o tratamento não tem efeito, independentemente do contexto.[22]
Bayes não viveu na mesma época que Fisher, Neyman e Pearson, mas a teoria bayesiana também tem sido utilizada no contexto de tomadas de decisão. Por exemplo, na medicina.[23][24]
Escolha da hipótese nula[editar | editar código-fonte]
Paul Meehl argumenta que a importância epistemológica da escolha da hipótese nula não foi reconhecida. Quando a hipótese nula é prevista pela teoria, um experimento mais preciso é um teste mais severo da teoria subjacente. Quando a hipótese nula é sem diferença ou sem efeito, um experimento mais preciso é um teste menos severo da teoria que motivou a realização da experiência.[25]
Os exemplos de escolha da hipótese nula incluem:
1778 – Pierre Laplace compara as taxas de nascimento de meninos e meninas em várias cidades europeias. Laplace afirma que é natural concluir que estas possibilidades estão quase na mesma proporção. Portanto, a hipótese nula de Laplace é que as taxas de nascimento de meninos e meninas devem ser iguais dada a sabedoria convencional.[9]
1900 – Karl Pearson desenvolve o teste qui quadrado para determinar se uma dada forma da curva de frequência descreverá eficientemente as amostras desenhadas a partir de dada população. Portanto, a hipótese nula é que a população é descrita por tal curva de frequência. Pearson usa um exemplo da quantidade de 5 e 6 nos dados do lançamento de dados de Weldon.[26]
1904 – Karl Pearson desenvolve o conceito de contingência para determinar se os resultados são independentes de um dado fator categórico. A hipótese nula é que duas coisas não estão relacionadas (por exemplo, formação de cicatrizes e taxas de morte por varíola).[27] Neste caso, a hipótese nula não é mais prevista pela teoria ou pela sabedoria convencional. Em vez disto, ela é prevista pelo princípio da indiferença que levou Fisher e outros a descartar o uso de probabilidades inversas.[28]
Variações[editar | editar código-fonte]
Embora a inferência frequentista e a inferência bayesiana tenham diferenças notáveis, o teste de hipóteses é um princípio fundamental de ambos os métodos. Os testes de hipótese definem um procedimento que controla (corrige) a probabilidade de se rejeitar a hipótese nula incorretamente. O procedimento baseia–se na probabilidade de ocorrer um conjunto de observações se a hipótese nula for verdadeira. Esta probabilidade de tomar uma decisão incorreta não é a probabilidade de a hipótese nula ser verdadeira, nem mesmo se qualquer hipótese alternativa for verdadeira. Isto contrasta com outras possíveis técnicas da teoria da decisão, em que hipótese nula e hipótese alternativa são tratadas em uma base mais igualitária.[29]
Uma abordagem bayesiana ingênua para o teste de hipóteses é basear as decisões na probabilidade a posteriori, mas isto falha quando as hipóteses pontuais e contínuas são comparadas.[30][31] Outras abordagens para a tomada de decisão como a teoria da decisão bayesiana tentam equilibrar as consequências das decisões incorretas dentre todas as possibilidades ao invés de se concentrarem em uma única hipótese nula. Uma série de outras abordagens para a tomada de decisão com base em dados estão disponíveis por meio da teoria da decisão e da decisão ótima, algumas das quais possuem propriedades desejáveis. Entretanto, o teste de hipóteses é uma abordagem dominante na análise de dados em muitos campos da ciência. As extensões dos testes de hipóteses incluem o estudo do poder dos testes de hipótese. Isto é, a probabilidade de se rejeitar a hipótese nula corretamente. Estas considerações podem ser usadas para determinar o tamanho da amostra antes da coleta de dados.[32]
Procedimentos para o teste de hipóteses[editar | editar código-fonte]

Teste de hipóteses usando região crítica[editar | editar código-fonte]
É possível adotar o seguinte procedimento ao estabelecer o teste de hipóteses:[33]
- Escolher a hipótese nula e a hipótese alternativa com base no problema.
- Estabelecer a estimativa de teste (média, desvio padrão, distribuição) para testar a hipótese nula a partir da teoria estatística e das informações disponíveis no problema.
- Determinar um valor para o erro do tipo I (nível de significância). Os valores comuns são 5% e 1%. Construir a região crítica com o valor do erro do tipo I, os parâmetros os quais deseja–se testar e os parâmetros obtidos do problema (a região crítica determinará se a hipótese nula será ou não será rejeitada).
- Retirar uma amostra da população. Fazer os cálculos para determinar o valor da estimativa de teste a partir das observações da amostra da população. Geralmente as observações seguem uma distribuição normal (estatística de teste Z) ou uma distribuição t de Student (estatística de teste t).
- Se o valor da estatística (por exemplo, de teste Z ou de teste t) pertencer à região crítica definida pelo nível de significância, rejeitar a hipótese nula. Em caso contrário, não rejeitar a hipótese nula.
- Para os casos em que não for possível rejeitar a hipótese nula, o procedimento pode ser repetido com diferentes valores para o nível de significância para dar maior precisão à decisão pelo cálculo da região crítica e da estatística de teste.
Teste de hipóteses usando p–valor[editar | editar código-fonte]
Há um caminho mais rápido para o teste de hipótese. Em vez de se construir uma região crítica, calcula–se diretamente o p–valor. O p–valor é uma estatística muito usada para sintetizar o resultado de um teste de hipóteses. Formalmente, o p–valor é definido como a probabilidade de obter–se uma estatística de teste igual ou mais extrema que a estatística observada a partir de uma amostra de uma população assumindo–se a hipótese nula como verdadeira. Na literatura, o p–valor também é chamado de probabilidade de significância.[34]
- Calcular a estatística de teste (por exemplo, de teste Z ou de teste t) a partir das observações.
- Calcular o p–valor.
- Rejeitar a hipótese nula, se e somente se o p–valor for menor que o nível de significância pré–estabelecido.
Equivalência[editar | editar código-fonte]
Testes de hipótese via região crítica ou p-valor são equivalentes. O primeiro procedimento era mais vantajoso no passado, quando tabelas de estatísticas de teste, com os limiares de probabilidade das distribuições mais comuns, eram mais facilmente acessíveis que recursos computacionais. Essas tabelas permitiam que decisões fossem tomadas sem cálculos mais complexos de probabilidade; o que era adequado para uso operacional ou em sala de aula, mas deficiente para a demonstração de resultados. O segundo procedimento é acessível por tabelas mais extensas ou por suporte computacional, nem sempre disponíveis. Hoje, os cálculos de probabilidade, úteis para a elaboração de relatórios, são trivialmente realizados com os softwares apropriados.[35]
Os procedimentos descritos são perfeitamente adequados para a computação. Eles negligenciam o projeto de considerações dos experimentos. É particularmente crítico que tamanhos apropriados de amostras sejam estimados antes da realização do experimento.[36][37]
Interpretação[editar | editar código-fonte]
Se o p–valor for menor que o nível de significância determinado ou se a estatística de teste observada estiver dentro da região crítica, então a hipótese nula é rejeitada. Há uma conclusão. No exemplo do julgamento no tribunal, seria como se as evidências fossem suficientes para rejeitar a inocência e aceitar a culpa do réu. Se o p–valor não for menor que o nível de significância determinado (se a estatística de teste observada estiver fora da região crítica), então o teste não tem resultado. Não há uma conclusão. Isto seria como se o juri não conseguisse chegar a um veredicto.[38] O pesquisador geralmente apresenta considerações adicionais nos casos em que o p–valor é próximo do nível de significância. Há algumas pessoas que acham útil pensar a estrutura do teste de hipóteses como análoga à prova matemática por contradição.[39]
É importante notar a diferença entre aceitar a hipótese nula e simplesmente falhar em rejeita–la.[40] O termo falhar em rejeitar destaca que a hipótese nula é assumida como verdadeira desde o início do teste. Se há falta de evidências, a hipótese nula simplesmente continua a ser assumida como verdadeira. O termo aceitar a hipótese nula pode sugerir que a hipótese nula foi provada simplesmente por não ter sido refutada, uma falácia lógica conhecida como argumento da ignorância.[41][42] A menos que um teste com poder particularmente alto seja usado, a ideia de aceitar a hipótese nula pode ser perigosa. Entretanto, o termo prevalece em toda a estatística em que o significado realmente pretendido é bem compreendido.[43]
Se a rejeição da hipótese nula justifica verdadeiramente a aceitação da hipótese de pesquisa, isso depende da estrutura da hipótese. Por exemplo, rejeitar a hipótese de que a pegada de uma grande pata originou–se de um urso não significa aceitar imediatamente a existência do pé grande. Os testes de hipótese enfatizam a rejeição, que é baseada na probabilidade em vez da aceitação. Isso requer mais etapas de lógica. De acordo com David Bakan, a probabilidade de rejeitar a hipótese nula é uma função de cinco fatores: se o teste tem uma ou duas caudas, o nível de significância, o desvio padrão, a quantidade da hipótese nula e o número de observações. Estes fatores são fontes de críticas, uma vez que os fatores sob controle do pesquisador confere aos resultados a aparência de subjetividade.[44]
Uso e importância[editar | editar código-fonte]
Os testes de hipóteses desempenham um papel importante em inferência estatística e em estatística como um todo. Em uma análise do artigo de Neyman e Pearson, o professor do Departamento de Estatística da Universidade da Califórnia chamado E. L. Lehmann afirma que o novo paradigma formulado no artigo de 1933 e os seus desenvolvimentos continuam a desempenhar um papel central tanto na teoria quanto na prática em estatística.[45]
As aplicações práticas do teste de hipóteses incluem:[46]
- Testar se mais homens que mulheres sofrem com pesadelos.
- Estabelecer autoria de documentos.
- Avaliar o efeito da lua cheia no comportamento.
- Determinar o intervalo no qual um morcego pode detectar um inseto pelo eco.
- Decidir se o carpete de hospital resulta em mais infecções.
- Selecionar os melhores meios para parar de fumar.
- Checar se adesivos refletem no comportamento de proprietários de carros.
- Testar as reivindicações de analistas de manuscritos.
O teste de significância é uma das ferramentas estatísticas favoritas de algumas ciências sociais experimentais (outras áreas têm favorecido a estimação de parâmetros como o tamanho de efeito), usado como substituto da comparação tradicional do valor previsto e do resultado experimental no método científico. Por exemplo, mais de 90% dos artigos do Journal of Applied Psychology no início da década de 1990.[47]
Cuidados[editar | editar código-fonte]
De acordo com David Moore, se o governo requeresse que procedimentos estatísticos apresentassem rótulos de advertência nos moldes daqueles contidos em medicamentos, a maioria dos métodos de inferência com certeza teria longos rótulos.[48] Estes cuidados aplicam–se aos testes de hipóteses e às suas alternativas. Um teste de hipóteses de sucesso está associado à probabilidade e à taxa de erro do tipo I (a conclusão de um teste de hipóteses depende da solidez da amostra). É muito importante o desenho do experimento, uma vez que efeitos inesperados podem ser observados.[49]
Estes efeitos inesperados incluem:
- O efeito do Hans esperto, em que um cavalo parecia ser capaz de fazer aritmética simples.[50][51]
- O efeito Hawthorne, em que trabalhadores industriais eram mais produtivos com melhor iluminação e menos produtivos com pior iluminação.[52][53]
- O efeito placebo, em que pílulas sem componentes medicamente ativos eram notadamente eficazes.[54][55]
Uma análise estatística de dados enganosos produz conclusões enganosas. A questão da qualidade dos dados pode ser mais sutil. Em previsões, não há concordância sobre a precisão de uma medida de previsão. Na ausência de uma medida de consenso, nenhuma decisão baseada em medições será tomada sem controvérsia. Um dos livros mais populares sobre estatística, Como Mentir com Estatística, não fala muito sobre teste de hipóteses, mas chama atenção para o fato que muitas alegações são feitas com base em amostras muito pequenas para convencer (se um relatório não menciona o tamanho da amostra, é preciso duvidar dele).[56][57][58]
Os testes de hipóteses agem como um filtro das conclusões estatísticas. Apenas os resultados que atendam a um limiar de probabilidade são publicáveis. A economia também age como um filtro de publicação. Somente os resultados favoráveis ao autor e à fonte de financiamento podem ser submetidos para publicação. O impacto das filtragens nas publicações é denominado viés de publicação.[59]
Por exemplo, os testes múltiplos (às vezes relacionados à mineração de dados) podem ser um problema. Nos testes múltiplos, uma variedade de testes para possíveis efeitos são aplicados a um único conjunto de dados e somente os testes que produzem um resultado significante são relatados.[60] Estes testes muitas vezes envolvem procedimentos de correção múltiplos que controlam a taxa de erro de família (FWER) ou a taxa de falsa descoberta (FDR).[61] É prudente tomar decisões críticas com base nos resultados de testes de hipóteses, considerando os detalhes dos procedimentos em vez da conclusão por si só.[62]
Exemplos[editar | editar código-fonte]
Mala radioativa[editar | editar código-fonte]
Considere que um contador Geiger, equipamento de medição de radioatividade, é colocado próximo a uma mala e marca 10 contagens por minuto. Normalmente existe uma radioatividade natural típica do ambiente proveniente do ar e de objetos inofensivos de cerca de 9 contagens por minuto. A hipótese nula é que não há material radioativo na mala. De acordo com a distribuição de Poisson com valor esperado 9, há cerca de 41% de chance de registrar 10 contagens por minuto ou mais. Portanto, podemos dizer que a mala é compatível com a hipótese nula (isto não garante que não há material radioativo, apenas que não há evidências suficientes para sugerir isto). Por outro lado, se a radiação ambiente típica fosse de 3 contagens por minuto, então, a chance de registrar 10 contagens por minuto ou mais em uma distribuição Poisson seria de apenas 0.1%. Isso faria com que a mala não seja compatível com a hipótese nula e que provavelmente existam outros fatores responsáveis pela alta medição.
O teste não acusa diretamente a presença de material radioativo. O teste declara que a afirmação que não há presença de material radioativo é improvável. O duplo negativo (refutando a hipótese nula) do método é confuso, mas usar um contra-exemplo para refutar a hipótese nula é a prática matemática padrão.[63]
Julgamento no tribunal[editar | editar código-fonte]
O procedimento de um teste estatístico é comparável ao julgamento de um crime. O réu não é considerado culpado na medida em que sua culpa não é provada. O promotor tenta provar a culpa do réu. Quando houver provas de acusação suficientes o réu é condenado. No início do procedimento, há duas hipóteses (o réu não é culpado) e (o réu é culpado). é a hipótese nula, aceita no momento (presunção da inocência). é a hipótese alternativa, a qual espera-se apoiar.[38]
A hipótese de inocência (Presunção da inocência) somente é rejeitada quando o erro é muito improvável, porque não se quer condenar um réu inocente. Este erro é chamado de erro do tipo I (isto é, a convicção de uma pessoa inocente) e a ocorrência deste erro é controlada para ser rara. Como uma consequência desde comportamento assimétrico, o erro do tipo II (absolver uma pessoa que cometeu um crime) muitas vezes é muito grande.[38]
| é verdadeira
(o réu não é culpado) |
é verdadeira
(o réu é culpado) | |
|---|---|---|
| Hipótese nula é aceita
(absolvição) |
Decisão certa | Decisão errada
(erro do tipo II) |
| Hipótese nula é rejeitada
(condenação) |
Decisão errada
(erro do tipo I) |
Decisão certa |
Um julgamento criminal pode considerar os procedimentos de decisão culpado e não culpado ou evidência e limiar. Por um lado, o réu é julgado. Por outro lado, o desempenho do promotor (o qual detém o ônus da prova) também é julgado. Portanto, um teste de hipóteses pode ser considerado tanto como o julgamento de uma hipótese quanto como o julgamento de uma evidência.[38]
Dama apreciadora de chá[editar | editar código-fonte]
Em um famoso exemplo de teste de hipóteses conhecido como dama apreciadora de chá, o autor Fisher diz que uma colega sua, Dra. Muriel Bristol, afirmou ser capaz de identificar se foi adicionado primeiramente leite ou chá à xícara.[64] Fisher propôs dar 8 xícaras (4 xícaras com leite adicionado primeiramente e 4 xícaras de com chá adicionado primeiramente) em ordem aleatória e perguntar qual a probabilidade de ela chegar ao resultado correto apenas com base nas probabilidades (a hipótese nula era que ela não teria esta capacidade). O teste estatístico era um conta simples de número do sucessos em selecionar quatro xícaras. A região crítica era o caso de quatro sucessos de quatro possibilidades baseadas em um critério de probabilidade convencional . Fisher afirmou que nenhuma hipótese alternativa era necessária. A dama identificou corretamente cada xícara, o que seria considerado um resultado estatisticamente significativo.[65]
Teste de clarividência[editar | editar código-fonte]
Uma pessoa é testada quanto ao seu poder de clarividência. É mostrada para a pessoa a parte de trás de 25 cartas de um baralho comum, de modo que ela precisa aceitar o naipe da carta. Denomina–se o número de acertos. Como deseja–se encontrar evidências do poder de clarividência da pessoa, a hipótese nula é que ela não possui esta habilidade e a hipótese alternativa é que ela possui esta habilidade, mesmo que em diferentes graus. Se a hipótese nula é válida, a pessoa pode apenas chutar um naipe.[66]
Como existem 4 naipes em um baralho comum, ela possui de chance de acertar o naipe.
Se a hipótese alternativa for válida, a pessoa pode acertar os naipes com probabilidade maior que .[66]
Sendo esta probabilidade, podemos construir o teste da seguinte maneira:
(a pessoa está chutando)
(a pessoa possui dom de clarividência)[66]
Quando a pessoa acertar todas as cartas, ela é considerada clarividente (a hipótese nula é rejeitada). O mesmo acontece para 24 ou 23 acertos. Entretanto, o que acontece para 19, 18 ou 17 acertos? Qual o valor crítico para considerar que a pessoa acertou o naipe das cartas devido à clarividência em vez da sorte? Como determinar o valor crítico?[67]
Por exemplo, se for escolhido o valor crítico , muito poucas pessoas testadas serão consideradas clarividentes. Entretanto, se for escolhido o valor crítico , um maior número de pessoas serão consideradas clarividentes. Na prática, quem constrói o teste é quem decide o valor crítico. Em outras palavras, escolher o valor crítico é definir o quão frequente serão os erros do tipo I (quantas pessoas acertam o valor crítico apenas com chutes, sem possuírem o poder de clarividência).[67]
É possível calcular a probabilidade para e , por exemplo:
Isto indica que com um valor crítico , a probabilidade de um falso positivo é muito maior.[68]
Porém, o que acontece se a pessoa não acertar nenhuma das cartas? Também pode existir uma clarividência reversa. A probabilidade de errar o naipe é de .[68]
Então, existem considerações diferentes no momento de construir o teste de hipóteses:
É bastante improvável que alguém erre todas as cartas. Entretanto, rejeitar a hipótese nula neste caso seria ignorar a característica da pessoa de evitar o naipe correto. É comum para este tipo de problema associar uma estatística para o erro do tipo II (afirmar que uma pessoa não tem o poder de clarividência quando ela tem esta capacidade). Uma solução seria considerar um nível de significância de 1% apenas se a pessoa conseguisse prever corretamente pelo menos 2 cartas (não teria uma probabilidade tão pequena quanto errar todas as cartas).[67]
Problema dos parafusos[editar | editar código-fonte]
Uma construtora utiliza um parafuso importado com propriedades específicas para a manutenção da qualidade das construções. A propriedade mais interessante é a resistência à tração. Há 2 empresas que fabricam este tipo de parafuso, de acordo com as especificações técnicas de seu país. O país A fabrica parafusos com resistência média à tração de 145 kg e desvio padrão de 12 kg. O país B fabrica parafusos com uma média 155 kg e desvio padrão 20 kg. Seja o leilão de um lote deste tipo de parafuso, que sobrou de uma obra em uma determinada região.[69]
Uma construtora interessada em comprar os parafusos precisa saber a origem deles para verificar se eles atendem às especificações do seu país. Um leiloeiro afirma que, antes do leilão, será divulgada a resistência média de uma amostra de 25 parafusos do lote. Como a construtora interessada em comprar os parafusos deve proceder para tomar sua decisão?[69]
Uma resposta coerente é analisar as médias. É possível estipular que para um valor menor que 150 kg (o meio termo entre as duas médias), os parafusos são do país A. Em caso contrário, os parafusos são do país B. No dia do leilão, a resistência média divulgada da amostra é de 148 kg. Isto é, os parafusos são do país A. Entretanto, esta conclusão não poderia ser enganosa? Não seria possível uma amostra de 25 parafusos do país B apresentar resistência média de 148 kg? Seja, portanto, o seguinte teste de hipóteses:
- : os parafusos são do país B. Isto é, a resistência média da amostra segue uma distribuição com média e desvio padrão .
- : os parafusos são do país A. Isto é, a resistência média da amostra segue uma distribuição com média e desvio padrão .
- Erro de tipo I: conclui–se que os parafusos são do país A, quando na verdade são do país B. A amostra do país B apresenta média inferior a 150 kg.
- Erro do tipo II: conclui–se que os parafusos são do país B, quando na verdade são do país A. A amostra do país A apresenta média superior a 150 kg.[68]
Então, é possível usar o teorema do limite central para estipular uma média (igual à média da população) e um desvio padrão para a amostra:
.[70]
Com a estatística de teste normal Z com os dados da amostra, é possível calcular a probabilidade do erro de tipo I e do erro de tipo II. Para a região crítica (RC), é possível utilizar valores menores ou iguais a 150 kg:
,
em que o valor para a estatística foi obtido a partir de uma tabela de distribuição normal padrão.[66]
Da mesma forma, é possível calcular o erro do tipo II. No entanto, é considerada distribuição do país A (com seu próprio desvio padrão da amostra):
Estes resultados indicam que para a regra de decisão definida, há maior probabilidade de se cometer o erro do tipo I em vez do erro do tipo II. Isto é, a regra de decisão privilegia a afirmação de que os parafusos são do país A.[69]
Porém, a construção do teste também está sujeita a erros. Como os valores do erro do tipo I e do erro do tipo II dependem apenas da média da amostra, é possível supor uma média para a qual obtém–se o mesmo valor de e a partir dos quais é possível tomar uma decisão com maior confiabilidade (esta decisão seria efetiva mesmo que houvesse parafusos de outros países no lote).[69]
Teste de redução de preço[editar | editar código-fonte]
Um comerciante que vende pela internet decidiu verificar se conseguiria aumentar seu lucro se reduzisse o preço da mercadoria. Para isso, estava disposto a reduzir o preço para um grupo aleatório de clientes que visitassem sua loja online (grupo de teste), manter o preço para os demais visitantes (grupo de controle) e medir a conversão de vendas de cada grupo. Na perspectiva do comerciante, o teste seria um sucesso se conseguisse confirmar que as vendas adicionais foram suficientes para compensar a redução do preço.
Esse teste é interessante porque não basta que o resultado mostre um aumento estatisticamente significativo na conversão de vendas, e nem tão pouco na receita, mas sim no lucro. Digamos que o preço da mercadoria atualmente é $ 70, a conversão de vendas é de 4% (ou seja, 4% dos visitantes compram a mercadoria) e o custo de produção da mercadoria é de $ 30. O comerciante quer testar o preço de $ 60. Então, podemos desenhar 3 hipóteses nulas:
- Não há aumento de vendas: Conversão do grupo de teste não é maior do que a do grupo de controle
- Não há aumento em receitas: Conversão do grupo de teste não é maior do que 4,67% (), que é o valor necessário para manter a mesma receita apesar da queda do preço.
- Não há aumento em lucro: Conversão do grupo de teste não é maior do que 5,33% (), que é o valor necessário para manter o mesmo lucro apesar da queda do preço.
| Controle | Teste | ||
|---|---|---|---|
| Preço | $ 70 | $ 60 | |
| Quantidade de visitantes no site | 8.000 | 2.000 | |
| Vendas | 320 | 120 | |
| Conversão de vendas | 4% | 6% |
Com esses dados, o comerciante pode tirar algumas conclusões sobre o resultado do teste usando a fórmula de teste z de duas proporções:
| Estatística z | p-valor | Conclusão considerando nível de significância de 0.05 | |
|---|---|---|---|
| Não há aumento de vendas | 0,0002 | rejeitada | |
| Não há aumento em receitas | 0,0101 | rejeitada | |
| Não há aumento em lucro | 0,1229 | não rejeitada |
Portanto, mesmo observando uma conversão de 6%, o comerciante ainda não tem confiança para concluir que a redução de preço vale a pena, do ponto de vista de aumento de lucros. Como alternativa, ele poderia deixar o teste vigorar por mais tempo ou aumentar a proporção de visitantes que serão expostos ao preço reduzido. Essas ações fariam com que diminuísse o denominador da estatística z, aumentando a confiança para rejeitar a hipótese nula.
Estatísticas de teste comuns[editar | editar código-fonte]
Teste de hipóteses com uma amostra – É apropriado para comparar a amostra com a população a partir da hipótese. As características da população são conhecidas a partir da teoria ou são calculadas a partir da população.[62]
Teste de hipóteses com duas amostras – É apropriado para comparar duas amostras, tipicamente amostra experimental e amostra de controle a partir de um experimento cientificamente controlado.[72]
Teste pareado – É apropriado para comparar duas amostras quando é impossível controlar variáveis importantes. Em vez de comparar dois conjuntos, os componentes são pareados entre amostras. Então, a diferença entre os componentes se torna a amostra. Tipicamente a média das diferenças é comparada a 0. O cenário comum de exemplo para quando o teste pareado é apropriado é quando um único conjunto de sujeitos de teste tem algo aplicado a eles e o teste destina-se a verificar um efeito.[73]
Teste Z – É apropriado para comparar médias por meio de condições mais rigorosas em relação à normalidade a um desvio padrão conhecido.[74]
Teste t – É apropriado para comparar médias por meio de condições mais relaxadas.[75]
Teste de proporção – É análogo aos testes de médias (proporção de 50%).[76]
Testes qui quadrado – Usam os mesmos cálculos e a mesma distribuição de probabilidade para diferentes aplicações:
- Testes qui quadrado para variância são usados para determinar se uma população normal tem uma variância específica. A hipótese nula é que a população normal tem a variância específica.[77]
- Testes qui quadrado para independência são usados para decidir se duas variáveis são associadas ou independentes. As variáveis são categóricas em vez de numéricas. A hipótese nula é que as variáveis são independentes. Os números usados no cálculo são as frequências observadas e esperadas de ocorrência (a partir de tabelas de contingência).[78]
- Testes qui quadrado de bondade de ajuste são usados para determinar a adequação das curvas ajustadas aos dados. A hipótese nula é que a curva ajustada é adequada. É comum determinar formatos de curvas para minimizar o erro quadrático médio. Então, é apropriado que o cálculo de bondade de ajuste some os erros quadráticos.[79]
Teste F – É comumente usado para decidir se agrupamentos de dados por categorias são significativos. A hipótese nula é que duas variâncias são as mesmas. Então, o agrupamento proposto não é significativo.[80]
Na tabela abaixo, os símbolos usados são definidos na última linha. Há mais testes que podem ser encontrados em outros artigos. Existem provas de que estas estatísticas de teste são apropriadas.[81]
| Teste | Fórmula | Notas | |||
|---|---|---|---|---|---|
| Teste Z para uma amostra | [82] |
| |||
| Teste Z para duas amostras | [83] |
| |||
| Teste t para uma amostra | [84] |
| |||
| Teste pareado | [85] |
| |||
| Teste t combinado para duas amostras com variâncias iguais | [86] |
| |||
| Teste t não combinado para duas amostras com variâncias desiguais (Teste t de Welch) | [88][87] |
| |||
| Teste Z de uma proporção | [89] |
| |||
| Teste Z de duas proporções combinado para | [90] |
| |||
| Teste Z de duas proporções não combinado para | [91] |
| |||
| Teste qui quadrado para variância | [92] |
| |||
| Teste qui quadrado de bondade de ajuste | [93] | ||||
| Teste F para duas amostras para igualdade de variâncias | [96] |
| |||
| Test t de regressão para | [96] |
| |||
| Em geral, o subscrito 0 indica um valor extraído da hipótese nula (), que deveria ser usado o máximo possível na construção do seu teste estatístico.
Definição de outros símbolos:
| |||||
Testes para a média[editar | editar código-fonte]
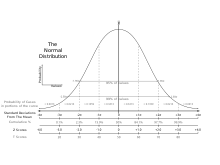
O teste de hipóteses consiste em verificar por meio de uma amostra se a média da população atende a um certo nível de significância.[2][6]
Inicialmente deve–se calcular
,
em que é a média da amostra, é a média esperada da população, é o desvio padrão da amostra e é o tamanho da amostra.[99]
Em seguida, consulta–se na tabela da curva normal o Z correspondente a cada caso. Finalmente, verifica–se se encontra–se na área de rejeição do teste de hipótese.[99]

Unilateral (unicaudal à esquerda)[editar | editar código-fonte]
Rejeita–se .[100]
Unilateral (unicaudal à direita)[editar | editar código-fonte]
Rejeita–se .[100]
Bilateral[editar | editar código-fonte]
Rejeita–se ou se .[100]
Terminologia[editar | editar código-fonte]
Seguem algumas definições baseadas no livro Testing Statistical Hypotheses, de E. L. Lehmann e Joseph P. Romano.[101]
Hipótese estatística – Afirmação sobre os parâmetros que descreve a população (não é a mesma coisa que amostra).[101]
Estatística – Valor calculado a partir de uma amostra geralmente para resumir a amostra para propósito de comparação.[101]
Hipótese simples – Qualquer hipótese que especifique completamente a distribuição da população.[101]
Hipótese composta – Qualquer hipótese que não especifique completamente a distribuição da população.[101]
Hipótese nula () – Hipótese simples associada a uma contradição de uma teoria que se gostaria de provar.[101]
Hipótese alternativa () – Hipótese geralmente composta associada a uma contradição de uma teoria que se gostaria de provar.[101]
Teste estatístico – Procedimento cujos inputs são as amostras e o resultado é a hipótese.[101]
Região de aceitação – Conjunto de valores do teste estatístico para o qual a hipótese nula não é rejeitada.[101]
Região de rejeição (região crítica) – Conjunto de valores do teste estatístico para o qual a hipótese nula é rejeitada.[101]
Valor crítico – Valor limite que delimita as regiões de aceitação e de rejeição para o teste estatístico.[101]
Poder de um teste () – Probabilidade do teste de se rejeitar corretamente a hipótese nula. β é o complemento da taxa de falsos negativos. O poder é denominado sensibilidade em bioestatística ("Este é um teste sensível. Porque o resultado é negativo, podemos afirmar com confiança que o paciente não tem a condição").[101]
Tamanho – Para hipóteses simples, é a probabilidade do teste de se rejeitar incorretamente a hipótese nula. É a taxa de falsos positivos. Para hipóteses compostas, é o supremo da probabilidade do teste de se rejeitar a hipótese sobre todos os casos cobertos pela hipótese nula. O componente da taxa de falsos positivos é denominado especificidade em bioestatística ("Este é um teste específico. Porque o resultado é positivo, podemos afirmar com confiança que o paciente tem a condição").[101]
Nível de significância de um teste () – O limite superior imposto sobre o tamanho de um teste. O seu valor é escolhido pelo estatístico antes de verificar os dados ou de escolher qualquer teste particular para ser utilizado. É a exposição máxima para se rejeitar erroneamente a hipótese nula.Testar a hipótese nula a um nível de significância α significa testar a hipótese nula por meio de um teste, cujo tamanho não excede α. Na maioria dos casos, usa–se testes cujos tamanhos são iguais aos níveis de significância.[101]
p–valor – Probabilidade do resultado ser pelo menos tão extremo quanto teste estatístico, assumindo que a hipótese nula é verdadeira.[101]
Teste de significância estatística – Predecessor ao teste de hipótese. Um resultado experimental é considerado estatisticamente significante se a amostra é suficientemente inconsistente com a hipótese nula. Isto foi considerado senso comum, uma heurística pragmática para identificar resultados experimentais significativos, uma convenção que estabelece um limite para a evidência estatística ou um método para tirar conclusões a partir dos dados. O teste de hipóteses adicionou rigor matemático e consistência filosófica ao conceito, tornando a hipótese alternativa explícita. O termo é pouco usado para descrever a versão moderna que agora é parte do teste de hipóteses.[101]
Teste conservador – Um teste é conservador se, quando construído para um dado nível de significância nominal, a probabilidade verdadeira de se rejeitar incorretamente a hipótese nula nunca é maior que o nível nominal.[101]
Teste exato – Um teste no qual o nível de significância ou o valor crítico podem ser calculados exatamente. isto é, sem qualquer aproximação. Em alguns contextos, o termo é restrito aos testes aplicados a dados categóricos e a testes de permutação nos quais os cálculos são realizados pela completa enumeração de todos os resultados possíveis e suas probabilidades. Um teste de hipóteses compara um teste estatístico (Z ou t, por exemplo) e um limite. O teste estatístico (fórmula encontrada na tabela abaixo) é baseada na otimalidade. os seguintes termos descrevem testes em termos desta otimalidade.[101]
Teste mais poderoso – Para um dado tamanho ou nível de significância, o teste com o maior poder (probabilidade de rejeição) para um dado valor de parâmetro(s) sendo testado contido na hipótese alternativa.[101]
Teste uniformemente mais poderoso – Um teste com o maior poder para todos os valores de parâmetro(s) testado contido na hipótese alternativa.[101]
Os métodos de Fisher, Neyman–Pearson e Bayes[editar | editar código-fonte]
O exemplo da mala radioativa. Se a mala realmente é blindada para o transporte de material radioativo, então um teste pode ser realizado para selecionar uma entre três hipóteses: nenhuma presença de material radioativo, presença de um material radioativo, presença de dois materiais radioativos. O lema do teste de hipóteses de Neyman–Pearson afirma que um bom critério para a seleção de hipóteses é a razão das suas probabilidades (uma razão de verossimilhança). Um método simples de solução é selecionar a hipótese com a maior probabilidade para as contagens de Geiger observadas. O resultado coincide com a intuição: uma pequena contagem implica nenhum material radioativo, enquanto que uma contagem intermediária implica um material radioativo e muitas contagens implicam dois materiais radioativos. O método Baseyano mantém os argumentos sobre a priori a qual é mais usada em conjunto com as priori conjugadas.[102]
A teoria de Neyman–Pearson pode acomodar as probabilidades prévias e os custos das ações resultantes das decisões.[103] O primeiro permite que cada teste considere os resultados dos testes anteriories, diferentemete dos testes de significância de Fisher. O último permite a consideração de questões econômicas, assim como de probabilidades. Bayes irá argumentar que é necessário uma priori, ou seja, a partir de um conhecimento prévio sobre o assunto e então é definido uma família paramétrica de densidade para os casos em que é preferível trabalhar com priori conjugadas. Uma razão de verossimilhança continua a ser um bom critério de seleção entre as hipóteses.[102]
Sobre Fisher e Neyman-Pearson, as duas formas de testes de hipóteses são baseadas em diferentes formulações de problemas. O teste original é análogo à questão de falso ou verdadeiro. O teste de Neyman–Pearson é mais parecido com a questão de múltipla escolha. Na visão de John Turkey, a primeira leva a conclusões com base apenas em evidências fortes, enquanto a última leva a decisões com base em evidências disponíveis.[104] Sobre Bayes, o argumento é sobre o que se conhece das malas radioativas. Por exemplo, se uma mala foi usada anterioremente para transportar uma material radioativo, então ela terá chances maiores de conter radioatividade.[105]
Fisher e Neyman-Pearson fazem testes os quais parecem ser muito diferentes tanto matematicamente quanto filosoficamente, desenvolvimentos posteriores levam a afirmações contrárias. Sejam várias fontes radiativas minúsculas. As hipóteses se tornam 0, 1, 2, 3, ... grãos de areia radioativa. Há pouca distinção entre nenhuma e alguma radiação (Fisher), 0 grãos de areia radioativa contra todas as alternativas (Neyman–Pearson) e, se a mala tem chance de conter radioatividade depois de ter sido ou não ter sido usada anteriormente (Bayes). On the Problem of the Most Efficient Tests of Statistical Hypotheses também considerou hipóteses compostas (aquelas cuja distribuição inclui um parâmetro desconhecido). Um exemplo mostrou a otimalidade do test t de Student. Segundo o trabalho de Neyman–Pearson publicado em 1933, não pode haver melhor teste para a hipótese em consideração. A teoria de Neyman–Pearson mostrava a otimalidade dos métodos fisherianos desde seu início.[13]
O teste de significância de Fisher provou–se uma ferramenta estatística popular flexível em aplicações com pouco potencial de crescimento matemático. O teste de hipóteses de Neyman–Pearson é reivindicado como um pilar da matemática estatística, com a criação de um novo paradigma para a área. Isto também estimulou novas aplicações em controle estatístico do procedimento, teoria da detecção, teoria da decisão e teoria dos jogos.[106] Ambas as formulações têm sido bem sucedidas, mas os sucessos têm tido caráteres diferentes. O método de Bayes tem boas aplicações sobre as condições vividas ou conhecimento adquirido por experiência como na medicina, em que um médico pode constatar que uma dor no pescoço pode levar a doença meningite. Enquanto o método de Bayes mostra que 1 a cada 5000 pessoas pode ter meningite com a evidência dor no pescoço.[107]
A disputa sobre as formulações não está resolvida. A ciência usa primeiramente a formulação de Fisher ligeiramente modificada, como ensinado pela estatística introdutória. Estatísticos estudam a teoria de Neyman–Pearson na pós–graduação. Os matemáticos consideram a união de ambas as formulações. Os filósofos consideram–nas separadamente. As diferentes opiniões consideram as formulações competitivas (Fisher contra Neyman), incompatíveis[8] ou complementares.[15] A terminologia é inconsistente. O teste de hipóteses pode significar qualquer mistura das formulações de Fisher e Neyman–Pearson, que podem mudaram com o passar do tempo (qualquer discussão sobre teste de significância contra teste de hipóteses é vulnerável à confusão). A disputa tornou–se ainda mais complexa, uma vez que a inferência bayesiana passou a ser ainda mais respeitada.[108]
Fisher pensou que o teste de hipóteses era uma estratégia útil para o controle de qualidade industrial, mas ele discordava veemente que o teste de hipóteses poderia ser útil para cientistas.[12] O teste de hipóteses fornece um meio para encontrar as estatísticas de teste, usadas em um teste de significância. O conceito de poder é útil para explicar as consequências do ajuste do nível de significância e é muito usado para determinar o tamanho da amostra. Fisher e Neyman-Pearson possuem métodos os quais continuam filosoficamente distintos. Eles geralmente (mas nem sempre) levam a mesma resposta matemática. A resposta preferível depende do contexto.[15] Enquanto a fusão das teorias de Fisher e de Neyman–Pearson tem sido pesadamente criticada, modificar a fusão para alcançar objetivos bayesianos tem sido considerado.[109]
| Teste da hipótese nula de Fisher | Teoria da decisão de Neyman e Pearson | Teoria da decisão de Bayes |
|---|---|---|
| 1. Estabelecer uma hipótese nula estatística. O nulo não precisa ser uma hipótese nula (isto é, diferença zero). | 1. Estabelecer duas hipóteses estatísticas, e . Decidir sobre , e tamanho da amostra antes do experimento, com base em considerações subjetivas de custo benefício. Isto define uma região de rejeição para cada hipótese. | 1. Considera-se a informação prévia sobre um evento ocorrer. Por exemplo, no lançamento de uma moeda, um observador diz que aquela moeda cai mais a face cara do que a face coroa. Então, considerar a maior probabilidade de cair cara é uma priori. Disso decorre a adequação da priori para uma distribuição de probabilidade (beta, normal, log normal, etc), sendo essa adequação a posteriori.[110] |
| 2. Registrar o nível de significância exato (por exemplo, ou ). Não usar o nível de significância convencional de 5%. Não mencionar sobre aceitar ou rejeitar hipóteses. Se o resultado não é significante, não tirar conclusões e não tomar decisões. Suspender julgamentos até que mais dados estejam disponíveis. | 2. Se o dado cair na região de rejeição de , aceitar . Em caso contrário, aceitar . Note–se que aceitar uma hipótese não significa acreditar nela. Isto significa apenas agir como se ela fosse verdadeira. | 2. Realizar uma aproximação de densidade e calcula a probabilidade.[110] |
| 3. Usar este procedimento apenas se souber pouco sobre o problema. Somente tirar conclusões provisórias no contexto de uma tentativa para entender a situação experimental. | 3. A utilidade do procedimento é limitada para situações em que tem–se uma disjunção de hipóteses (por exemplo, ou é verdadeiro) e podem–se fazer concessões significativas de custo benefício para escolher e . | 3. Utilização ampla nos setores da sociedade.[111] |
Teste de comparação múltipla para teste de hipóteses[editar | editar código-fonte]
Para testes de hipóteses, o problema de comparações múltiplas (também conhecido como problema de testes múltiplos) resulta do aumento do erro do tipo I que ocorre quando os testes são usados repetidamente. Se comparações independentes foram realizadas, o nível de significância do experimento (também chamado taxa de erro da família) é dado por [112] Consequentemente, a menos que os testes sejam perfeitamente e positivamente dependentes, aumenta conforme o número de comparações aumenta. Se as comparações não forem independentes, também é possível afirmar que , seguindo a desigualdade de Boole.[113][114]
Há diferentes formar de garantir que a taxa de erro da família seja . O método mais conservador, que é livre de dependência e suposições distributivas é a correção de Bonferroni . Uma correção menos conservadora pode ser obtida resolvendo a equação para a taxa de erro da família de comparações independentes para . Isto resulta em , que é conhecido como a correção de Šidák. Outro procedimento é o método de Holm–Bonferroni, que tem mais poder que a correção de Bonferroni testando apenas o menor p–valor () contra o critério mais rigoroso e o maior p–valor () contra o critério menos rigoroso .[115]
Correção de Bonferroni[editar | editar código-fonte]
Em estatística, a correção de Bonferroni é um dos vários métodos utilizados para neutralizar o problema das comparações múltiplas. O teste de hipóteses é baseado na rejeição da hipótese nula se a probabilidade dos dados observados ficar abaixo da hipótese nula for baixa. Se as múltiplas comparações forem feitas ou se as múltiplas hipóteses forem testadas, a chance de acontecer um evento raro aumenta e, portanto, a probabilidade de rejeitar–se incorretamente a hipótese nula também aumenta. Isto é, a chance de ocorrer erro do tipo I aumenta.[116] A correção de Bonferroni compensa este aumento por meio do teste de cada hipótese individual em um nível de significância de , em que é o nível total desejado e é o número de hipóteses. Por exemplo, se foram testadas com , então a correção de Bonferroni testaria cada hipótese individual com .[117]
Desigualdade de Bonferroni[editar | editar código-fonte]
Em teoria das probabilidades, a desigualdade de Boole afirma que para qualquer conjunto finito de eventos a probabilidade de pelo menos um dos eventos acontecer não é maior que a soma das probabilidades dos eventos individuais. A desigualdade de Boole pode ser generalizada para encontrar os limites superiores e inferiores da probabilidade de um conjunto finito de eventos. Estes limites são conhecidos como desigualdades de Bonferroni.[118]
Sejam
e
,
para todos os inteiros em .[118]
Para ímpares em ,
Para pares em ,
A desigualdade de Boole é recuperada estabelecendo–se . Quando , a igualdade se mantém e a identidade resultante é o princípio da inclusão–exclusão.[119]
Método de Holm–Bonferroni[editar | editar código-fonte]
Em estatística, o método de Holm–Bonferroni (também chamado método de Holm ou método de Bonferroni–Holm) é usado para neutralizar o problema das comparações múltiplas. Pretende–se controlar a taxa de erro da família e oferece–se um teste simples uniformemente mais poderoso que a correção de Bonferroni. É um dos primeiros usos de stepwise algorithms em inferência simultânea.[120][121]
O método de Holm–Bonferroni segue os seguintes passos:
- Seja a família de hipóteses e os p–valores correspondentes;
- Os p–valores são ordenados em ordem crescente , sendo as hipóteses associadas;
- Para um dado nível de significância , seja o índice mínimo para o qual ;
- As hipóteses nulas são rejeitadas e as hipóteses não são rejeitadas;
- Se , então nenhuma hipótese nula é rejeitadas. Se não existir nenhum , então todas as hipóteses nulas são rejeitadas.[122][123]
Correção de Šidák[editar | editar código-fonte]
Em estatística, a correção de Šidák ou correção de Dunn–Šidák é um método utilizado para neutralizar o problema das comparações múltiplas. É um método simples de controlar a taxa de erro da família. Quando todas as hipóteses nulas são verdadeiras, o método fornece o controle do erro da família exato para testes que são estocasticamente independentes. É conservador para testes que são positivamente dependentes e é liberal para testes que são negativamente dependentes.[124]
Críticas[editar | editar código-fonte]
Muitas das críticas sobre o teste de hipóteses estatístico podem ser resumidas da seguinte maneira:[125][126][127][128][129][130]
- A interpretação do p–valor depende da regra da parada (stopping rule) e da definição de comparação múltipla. A primeira muda no curso de um estudo. A segunda é inevitavelmente ambígua. Isto é, o p–valor depende tanto do [dado] observado quanto dos outros possíveis [dados] que podem ter sido observados, mas não foram.[131]
- A confusão parcialmente resultante da combinação dos métodos de Fisher e de Neyman–Pearson, que são conceitualmente diferentes.[104]
- Ênfase na significância estatística para exclusão da estimação e confirmação por experiências repetidas.[132]
- Exigência rígida da significância estatística como um critério para publicação, resultando no viés da publicação. A maioria das críticas é indireta. Em vez de errados, os testes de hipóteses estatísticos são mal interpretados, excessivamente utilizados ou mal utilizados.[133]
- Quando usados para detectar se existe diferença entre dois grupos, surge um paradoxo. Quanto mais melhorias no projeto experimental (por exemplo, maior precisão de medidas e tamanho de amostra), mais lenientes tornam–se os testes de hipótese. A menos que aceite–se a declaração absurda que todas as fontes de ruídos nos dados sejam completamente anuladas, a chance de encontrar significância estatística em qualquer direção aproxima–se de 100%.[134]
- Há várias preocupações filosóficas. A probabilidade de significância estatística é uma função de decisões feitas por analistas e pesquisadores.[44] Se as decisões forem baseadas em uma convenção, elas são chamadas de arbitrárias.[135] Em caso contrário, elas podem ser denominadas subjetivas. Para minimizar os erros do tipo II, grandes amostras são recomendadas. Na psicologia, praticamente todas as hipóteses nulas são afirmadas como sendo falsas para amostras suficientemente grandes. Então, geralmente é sem sentido realizar um experimento com o único objetivo de rejeitar a hipótese nula.[136] Na psicologia, descobertas estatisticamente significantes são muitas vezes mal interpretadas.[137] Como a significância estatística não implica significância prática e a correlação não implica causalidade, a dúvida sobre a hipótese nula está longe de apoiar diretamente a hipótese de pesquisa.[138][139]
- O teste de hipóteses não nos diz o que queremos saber. Há várias reclamações deste tipo entre pesquisadores.[140][129][141][142]
Os críticos e os apoiadores estão em grande parte de acordo com as características do teste de significância de hipótese nula. Embora forneça informação crítica, é inadequado como a única ferramenta para análise estatística. Rejeitar com êxito a hipótese nula pode não oferecer suporte para a hipótese de pesquisa. A controvérsia contínua trata da seleção da melhor prática estatística para o futuro de curto prazo, dadas as práticas existentes (muitas vezes pobres). Os críticos prefeririam banir completamente o teste de significância de hipótese nula. Os apoiadores sugeririam uma mudança menos radical.
As controvérsias em torno do teste de significância e os seus efeitos sobre o viés em publicações particularmente têm produzido vários resultados. Nos Estados Unidos, a American Psychological Association fortaleceu suas exigências para relatórios estatísticos depois de revisão,[143] editoras de publicações médicas reconheceram a obrigação da publicação de alguns resultados que não são estatisticamente significantes para combater o viés em publicações[144] e o Journal of Articles in Support of the Null Hypothesis foi criado para publicar estes resultados exclusivamente.[145] Os textos adicionaram algumas preocupações e aumentaram a cobertura para ferramentas necessárias para estimar o tamanho da amostra exigido para produzir resultados significativos. As principais organizações não abandonaram o uso de testes de significância, embora algumas tenham discutido o assunto.[143]
Alternativas[editar | editar código-fonte]
As numerosas críticas ao teste de significância não levam a uma única alternativa. Uma posição unificadora dos críticos é que as estatísticas não deveriam levar a uma conclusão ou a uma decisão, mas a uma probabilidade ou a um valor estimado com um intervalo de confiança em vez de uma decisão aceitação–rejeição em relação a uma hipótese em particular. É improvável que a controvérsia em torno do teste de significância seja resolvida no futuro próximo. As suas supostas falhas e impopularidade não eliminam a necessidade de um meio objetivo e transparente para chegar a conclusões sobre os estudos que produzem resultados estatísticos. Os críticos não se unificaram em torno de uma alternativa. Outras formas de reportar a confiança ou a incerteza poderiam provavelmente aumentar em popularidade. Uma forte crítica ao teste de significância sugere uma lista de alternativas, envolvendo tamanhos de efeito para importância, intervalos de previsão para confiança, repetições e extensões para replicação, meta–análises para generalidade.[146] Nenhuma destas alternativas sugeridas produz uma conclusão ou uma decisão. E. L. Lehmann afirma que a teoria do teste de hipóteses pode ser apresentada em termos de conclusão ou de decisão, probabilidade ou intervalos de confiança (a distinção entre as abordagens é em grande parte relato e interpretação).[147]
Em uma alternativa, não há discordância. De acordo com Fisher, em relação ao teste de significância, podemos afirmar que um fenômeno é experimentalmente demonstrável quando sabemos como conduzir um experimento que raramente falhará em nos fornecer um resultado estatisticamente significante.[64] Segundo Jacob Cohen, não há necessidade de procurar por uma alternativa mágica ao teste de significância de hipótese nula porque ela não existe. Para o influente crítico do teste de significância, dados os problemas da indução estatística, devemos finalmente confiar como as antigas ciências na replicação.[140] A alternativa ao teste de significância é um teste repetido. A forma mais fácil de diminuir a incerteza estatística é por meio da obtenção de mais dados, pelo aumento do tamanho da amostra ou por testes repetidos. Raymond Nickerson afirmou nunca ter visto a publicação de uma experiência literalmente replicada em psicologia. Uma abordagem indireta para a replicação é a meta–análise.[141]
A inferência bayeseana é uma alternativa proposta ao teste de significância. Nickerson citou dez fontes com esta sugestão, incluindo Rozeboom (1960).[141] Por exemplo, a estimação de parâmetros bayeseanos pode fornecer informações importantes sobre os dados, a partir dos quais os pesquisadores podem desenhar inferências ao mesmo tempo em que utilizam dados incertos que exercem apenas influência mínima sobre os resultados quando dados suficientes estão disponíveis. O psicólogo John K. Kruschke sugeriu a estimação bayeseana como uma alternativa para o teste t.[148] De outra maneira, dois modelos modelos ou hipóteses concorrentes podem ser comparados usando fatores bayeseanos.[149] Os métodos bayeseanos podem ser criticados por requerer informações raramente disponíveis nos casos em que os testes de significância são mais utilizados. Nem as probabilidades anteriores nem a distribuição de probabilidade da estatística de teste sob a hipótese alternativa muitas vezes estão disponíveis nas ciências sociais.[141]
Defensores da abordagem bayeseana às vezes afirmam que o objetivo de um pesquisador é na maioria das vezes avaliar objetivamente a probabilidade de uma hipótese ser verdadeira com base nos dados coletados.[150][151] Nem o teste de significância de Fisher nem o teste de hipóteses de Neyman–Pearson podem fornecer esta informação. A probabilidade de uma hipótese ser verdadeira apenas pode ser derivada a partir do uso do teorema de Bayes, que foi insatisfatória tanto para a área de Fisher quanto para o campo de Neyman–Pearson devido ao uso explícito da subjetividade na forma de probabilidade prévia. A estratégia de Fisher é evitar isto com o p–valor (um índice objetivo baseado nos dados sozinhos) seguida por inferência indutiva, enquanto Neyman–Pearson inventou sua abordagem de comportamento indutivo.[13][152]
Filosofia[editar | editar código-fonte]
O teste de hipóteses e a filosofia se cruzam. A estatística inferencial, que inclui o teste de hipóteses, é a probabilidade aplicada. A probabilidade e sua aplicação estão entrelaçadas com a filosofia. O filósofo David Hume escreveu que "todo conhecimento degenera em probabilidade". Definições práticas concorrentes de probabilidade refletem diferenças filosóficas. A aplicação mais comum do teste de hipóteses é na interpretação científica de dados experimentais, os quais são naturalmente estudados pela filosofia da ciência. Fisher e Neyman opunham–se à subjetividade da probabilidade. As suas visões contribuíram para as definições objetivas. O núcleo da discordância histórica deles era filosófico. Muitas das críticas filosóficas aos testes de hipóteses são discutidas por estatísticos em outros contextos, particularmente correlação não implica causação e desenho dos experimentos. Os testes de hipóteses estão sob contínuo interesse dos filósofos.[17][153]
Educação[editar | editar código-fonte]
Estatística é cada vez mais ensinada nas escolas, com o teste de hipóteses sendo um dos elementos ensinados.[154][155] Muitas conclusões reportadas na imprensa (desde pesquisas de opinião políticas a estudos médicos) são baseados em estatística. Um público informado deveria entender as limitações das conclusões estatísticas e muitas áreas de estudos na graduação requerem um curso de estatística pelo mesmo motivo.[156][157] Na graduação, a estatística introdutória dá muita ênfase ao teste de hipóteses (talvez metade de um curso típico). Áreas de estudo como literatura e religião agora incluem descobertas baseadas em análises estatísticas. As aulas de estatística introdutória ensinam o teste de hipóteses como um procedimento de um livro de receita. O teste de hipóteses também é ensinado na pós–graduação. Estatísticos aprendem como criar bons precedimentos de testes estatísticos (Z, t de Student, F e qui–quadrado). O teste de hipóteses estatístico é considerado uma área madura dentro da estatística, mas uma quantidade limitada de desenvolvimento continua.[147]
O método de livro de receita para ensinar estatística introdutória não deixa tempo para história, filosofia ou controvérsia. O teste de hipóteses tem sido ensinado como um método unificado. Pesquisas mostraram que graduandos foram enchidos com mal entendidos filosóficos em todos os aspectos da inferência estatística, que persistiram entre instrutores.[158] Embora o problema tenha sido resolvido há mais de uma década[159] e reivindicações para reformas educaionais continuem,[160] estudantes ainda se formam em estatística mantendo conceitos errôneos sobre os testes de hipóteses.[161] Ideias para melhorar o ensino do teste de hipóteses incluem encorajar os estudantes a pesquisarem erros estatísticos em trabalhos publicados, ensinar a história da estatística e enfatizar a controvérsia em uma disciplina geralmente dura.[162]
Ver também[editar | editar código-fonte]
Referências
- ↑ A. Gabriel, Franklin; K. Iyer, Hariharan; K. Burdick, Richard (1998). Applied Statistics: A First Course in Inference (em inglês). [S.l.]: Prentice Hall. p. 181. 461 páginas. ISBN 9780136214670
- ↑ a b Dávila, Víctor Hugo Lachos. «Teste de Hipóteses» (PDF). Universidade Estadual de Campinas (UNICAMP). p. 3. Consultado em 13 de abril de 2017
- ↑ «Teste de Fisher». Portal Action. p. 1. Consultado em 13 de abril de 2017
- ↑ Barros, Monica. «Teoria da Decisão: Neyman-Pearson e Bayes» (PDF). M. Barros Consultoria. p. 10. Consultado em 13 de abril de 2017
- ↑ EHLERS, RICARDO S. (2011). «INFERÊNCIA BAYESIANA» (PDF). ICMC São Carlos. p. 1. Consultado em 13 de abril de 2017
- ↑ a b «Inferência Estatística». Universidade Federal do Paraná (UFPR). Consultado em 4 de maio de 2017
- ↑ a b «Introdução à Inferência Estatística» (PDF). Universidade Federal de São Carlos (UFSCar). p. 79. Consultado em 4 de maio de 2017. Arquivado do original (PDF) em 26 de outubro de 2017
- ↑ a b Raymond Hubbard, M. J. Bayarri, P Values are not Error Probabilities Arquivado em 4 de setembro de 2013, no Wayback Machine.. A working paper that explains the difference between Fisher's evidential p-value and the Neyman–Pearson Type I error rate .
- ↑ a b Laplace, P (1778). «Mémoire Sur Les Probabilités» (PDF). Memoirs de l'Academie royale des Sciences de Paris. 9: 227–332
- ↑ Stigler, Stephen M. (1986). The History of Statistics: The Measurement of Uncertainty before 1900. Cambridge, Mass: Belknap Press of Harvard University Press. p. 134. ISBN 0-674-40340-1
- ↑ Moura, Nathália Demétrio Vasconcelos (2014). «Utilidade para testes de signicância» (PDF). Instituto de Matemática e Estatística - USP. pp. 7 – 8. Consultado em 26 de abril de 2017
- ↑ a b Fisher, R (1955). «Statistical Methods and Scientific Induction» (PDF). Journal of the Royal Statistical Society, Series B. 17 (1): 69–78
- ↑ a b c d Neyman, J; Pearson, E. S. (1 de janeiro de 1933). «On the Problem of the most Efficient Tests of Statistical Hypotheses». Philosophical Transactions of the Royal Society A. 231 (694–706): 289–337. doi:10.1098/rsta.1933.0009
- ↑ Goodman, S N (15 de junho de 1999). «Toward evidence-based medical statistics. 1: The P Value Fallacy». Ann Intern Med. 130 (12): 995–1004. PMID 10383371. doi:10.7326/0003-4819-130-12-199906150-00008
- ↑ a b c Lehmann, E. L. (1993). «The Fisher, Neyman–Pearson Theories of Testing Hypotheses: One Theory or Two?». Journal of the American Statistical Association. 88 (424): 1242–1249. doi:10.1080/01621459.1993.10476404
- ↑ Fisher, R N (1958). «The Nature of Probability» (PDF). Centennial Review. 2: 261–274"We are quite in danger of sending highly trained and highly intelligent young men out into the world with tables of erroneous numbers under their arms, and with a dense fog in the place where their brains ought to be. In this century, of course, they will be working on guided missiles and advising the medical profession on the control of disease, and there is no limit to the extent to which they could impede every sort of national effort."
- ↑ a b Lenhard, Johannes (2006). «Models and Statistical Inference: The Controversy between Fisher and Neyman–Pearson». Brit. J. Phil. Sci. 57: 69–91. doi:10.1093/bjps/axi152
- ↑ Neyman, Jerzy (1967). «RA Fisher (1890—1962): An Appreciation.». Science. 156.3781: 1456–1460. doi:10.1126/science.156.3781.1456
- ↑ Losavich, J. L.; Neyman, J.; Scott, E. L.; Wells, M. A. (1971). «Hypothetical explanations of the negative apparent effects of cloud seeding in the Whitetop Experiment.». Proceedings of the U.S. National Academy of Sciences. 68: 2643–2646. doi:10.1073/pnas.68.11.2643
- ↑ a b Halpin, P F; Stam, HJ (2006). «Inductive Inference or Inductive Behavior: Fisher and Neyman: Pearson Approaches to Statistical Testing in Psychological Research (1940–1960)». The American Journal of Psychology. 119 (4): 625–653. JSTOR 20445367. PMID 17286092. doi:10.2307/20445367
- ↑ Gigerenzer, Gerd; Swijtink, Zeno; Porter, Theodore; Daston, Lorraine; Beatty, John; Kruger, Lorenz (1989). «Part 3: The Inference Experts». The Empire of Chance: How Probability Changed Science and Everyday Life. [S.l.]: Cambridge University Press. pp. 70–122. ISBN 978-0-521-39838-1
- ↑ Loftus, G R (1991). «On the Tyranny of Hypothesis Testing in the Social Sciences» (PDF). Contemporary Psychology. 36 (2): 102–105. doi:10.1037/029395
- ↑ Martins, Maria Eugénia da Graça. «Karl Pearson». ALEA. p. 1. Consultado em 30 de maio de 2017
- ↑ Pena, Sérgio Danilo (2006). «Bayes: O 'cara'!» (PDF). Instituto de Biociências da USP. Consultado em 30 de maio de 2017
- ↑ Meehl, P (1990). «Appraising and Amending Theories: The Strategy of Lakatosian Defense and Two Principles That Warrant It» (PDF). Psychological Inquiry. 1 (2): 108–141. doi:10.1207/s15327965pli0102_1
- ↑ Pearson, K (1900). «On the criterion that a given system of deviations from the probable in the case of a correlated system of variables is such that it can be reasonably supposed to have arisen from random sampling» (PDF). Philosophical Magazine Series. 5 (50): 157–175. doi:10.1080/14786440009463897
- ↑ Pearson, K (1904). «On the Theory of Contingency and Its Relation to Association and Normal Correlation» (PDF). Drapers' Company Research Memoirs Biometric Series. 1: 1–35
- ↑ Zabell, S (1989). «R. A. Fisher on the History of Inverse Probability». Statistical Science. 4 (3): 247–256. JSTOR 2245634. doi:10.1214/ss/1177012488
- ↑ Barros, Monica. «Teoria da decisão: Neyman-Pearson e Bayes» (PDF). mbarros. p. 1. Consultado em 2 de junho de 2017
- ↑ Schervish, M (1996) Theory of Statistics, p. 218. Springer ISBN 0-387-94546-6
- ↑ Kaye, David H.; Freedman, David A. (2011). «Reference Guide on Statistics». Reference Manual on Scientific Evidence 3 ed. Eagan, MN Washington, D.C: West National Academies Press. p. 259. ISBN 978-0-309-21421-6
- ↑ REIS, MARCELO MENEZES. «PODER DO TESTE» (PDF). UFSC. p. 3. Consultado em 2 de junho de 2017
- ↑ Bussab, Wilton de O.; Morettin, Pedro A. (2004). Estatística Básica 5ª ed. [S.l.]: Saraiva. p. 332. 537 páginas
- ↑ Bussab, Wilton de O.; Morettin, Pedro A. (2004). Estatística Básica 5ª ed. [S.l.]: Saraiva. 343 páginas
- ↑ Triola, Mario (2001). Elementary statistics 8 ed. Boston: Addison-Wesley. p. 388. ISBN 0-201-61477-4
- ↑ Hinkelmann, Klaus; Kempthorne, Oscar (2008). Design and Analysis of Experiments. I and II Second ed. [S.l.]: Wiley. ISBN 978-0-470-38551-7
- ↑ Montgomery, Douglas (2009). Design and analysis of experiments. Hoboken, N.J.: Wiley. ISBN 978-0-470-12866-4
- ↑ a b c d Bolfarine, Heleno; Sandoval, Mônica Carneiro. Introdução à Inferência Estatística. [S.l.: s.n.] pp. 91—92. 126 páginas
- ↑ http://www.math.uah.edu/stat/hypothesis/Introduction.html
- ↑ «2. Testes de Hipóteses». Universidade Federal do Paraná (UFPR). Consultado em 4 de maio de 2017
- ↑ «Philosophy 103: Introduction to Logic - Argumentum ad Ignorantiam» (em inglês). philosophy lander. 24 de setembro de 2009. Consultado em 18 de julho de 2011
- ↑ Leônidas Hegenberg; Flávio E. Novaes Hegenberg (2009). Argumentar. Editora E-papers. p. 376. ISBN 978-85-7650-224-1.
- ↑ «6. Testes de Hipóteses». Universidade Federal do Paraná (UFPR). Consultado em 4 de maio de 2017
- ↑ a b Bakan, David (1966). «The test of significance in psychological research». Psychological Bulletin. 66 (6): 423–437. doi:10.1037/h0020412
- ↑ Lehmann, E. L. (1993). «The Fisher, Neyman—Pearson Theories of Testing Hypotheses: One Theory or Two?» (PDF). Journal of the American Statistical Association. 88 (424)
- ↑ Larsen, Richard J.; Stroup, Donna Fox (1976). Statistics in the Real World: a book of examples. [S.l.]: Macmillan. ISBN 978-0023677205
- ↑ Hubbard, R.; Parsa, A. R.; Luthy, M. R. (1997). «The Spread of Statistical Significance Testing in Psychology: The Case of the Journal of Applied Psychology». Theory and Psychology. 7 (4): 545–554. doi:10.1177/0959354397074006
- ↑ Moore, David (2003). Introduction to the Practice of Statistics. New York: W.H. Freeman and Co. p. 426. ISBN 9780716796572
- ↑ «Conductiing Experiments» (PDF). Consultado em 4 de maio de 2017
- ↑ «Clever Hans Phenomenon». The Skeptic's Dictionary. Consultado em 4 de maio de 2017
- ↑ Shaughnessy, John J.; Zechmeister, Eugene B.; Zechmeister, Jeanne S. (2012). Metodologia de Pesquisa em Psicologia 9ª ed. [S.l.]: AMGH. p. 46. 486 páginas
- ↑ McCarney R, Warner J, Iliffe S, van Haselen R, Griffin M, Fisher P; Warner; Iliffe; Van Haselen; Griffin; Fisher (2007). «The Hawthorne Effect: a randomised, controlled trial». BMC Med Res Methodol. 7. 30 páginas. PMC 1936999
 . PMID 17608932. doi:10.1186/1471-2288-7-30
. PMID 17608932. doi:10.1186/1471-2288-7-30
- ↑ Fox NS, Brennan JS, Chasen ST; Brennan; Chasen (2008). «Clinical estimation of fetal weight and the Hawthorne effect». Eur. J. Obstet. Gynecol. Reprod. Biol. 141 (2): 111–4. PMID 18771841. doi:10.1016/j.ejogrb.2008.07.023
- ↑ «placebo effect». Mirriam-Webster Incorporated. Consultado em 21 de janeiro de 2017
- ↑ «placebo effect». Consultado em 21 de janeiro de 2017
- ↑ "Over the last fifty years, How to Lie with Statistics has sold more copies than any other statistical text." J. M. Steele. ""Darrell Huff and Fifty Years of How to Lie with Statistics". Statistical Science, 20 (3), 2005, 205–209.
- ↑ Huff, Darrell (1993). How to lie with statistics. New York: Norton. ISBN 0-393-31072-8
- ↑ Huff, Darrell (1991). How to Lie with Statistics. London: Penguin Books. ISBN 0-14-013629-0
- ↑ Borenstein, Michael; Hedges, L. V.; Higgins, J. P. T.; Rothstein, H. R. (2009). «30. Publication Bias». Introduction to Meta—Analysis. [S.l.]: John Wiley & Sons. 452 páginas
- ↑ Goldman, Megan (2008). «Why is Multiple Testing a Problem?» (PDF). Universidade da Califórnia — Berkley. Consultado em 4 de maio de 2017
- ↑ «Lecture 10: Multiple Testing» (PDF). Universidade de Washington. Consultado em 4 de maio de 2017
- ↑ a b Bessegato, Lupércio F. «Testes de Hipóteses para uma Única Amostra» (PDF). Consultado em 18 de maio de 2017
- ↑ Shields, Morgan (13 de agosto de 2019). Research Methodology and Statistical Methods (em inglês). [S.l.]: Scientific e-Resources. p. 213
- ↑ a b Fisher, Sir Ronald A. (1956) [1935]. «Mathematics of a Lady Tasting Tea». The World of Mathematics. 3. [S.l.]: Courier Dover Publications. ISBN 978-0-486-41151-4 Originalmente do livro Design of Experiments de Fisher
- ↑ Box, Joan Fisher (1978). R.A. Fisher, The Life of a Scientist. New York: Wiley. p. 134. ISBN 0-471-09300-9
- ↑ a b c d Spiegel, Murray R. (2006). Estatística. São Paulo: Pearson. 267 páginas
- ↑ a b c Bussab, Wilton de O.; Morettin, Pedro A. (2014). Estatística básica. São Paulo: Saraiva. 337 páginas
- ↑ a b c d e Magalhães, Marco Nascimento; Lima, Antonio Carlos Pedroso (2002). Noções de probabilidade e estatística. São Paulo: EdUSP. 250 páginas
- ↑ a b c d Farber, Larson (2010). Estatística aplicada. São Paulo: Pearson. p. 293
- ↑ Spiegel, Murray R. (2006). Estatística. São Paulo: Pearson. pp. 104 – 109
- ↑ Witte, Robert S.; Witte, John S. (2005). Estatística. São Paulo: LTC. 213 páginas
- ↑ Bessegato, Lupércio F. «Inferência Estatística para Duas Amostras» (PDF). Consultado em 18 de maio de 2017
- ↑ «Amostras Pareadas». Universidade Federal do Paraná (UFPR). Consultado em 18 de maio de 2017
- ↑ «Teste Z». Universidade Federal do Paraná (UFPR). Consultado em 18 de maio de 2017
- ↑ «Teste t». Universidade Federal do Paraná (UFPR). Consultado em 18 de maio de 2017
- ↑ Dávila, Víctor Hugo Lachos. «Teste de Hipóteses» (PDF). Instituto de Matemática e Estatística da Universidade de São Paulo (IME / USP). Consultado em 18 de maio de 2017
- ↑ Vialli, Lorí. «Teste de Hipóteses» (PDF). Pontifícia Universidade Católica do Rio Grande do Sul (PUC – RS). p. 12. Consultado em 18 de maio de 2017
- ↑ «Testes Qui-Quadrado – Aderência e Independência» (PDF). Instituto de Matemática e Estatística da Universidade de São Paulo (IME / USP). Consultado em 18 de maio de 2017
- ↑ «Teste Qui-Quadrado de Bondade de Ajuste – Distribuições Poisson e Normal» (PDF). Instituto de Ciências Matemáticas e de Computação da Universidade de São Paulo (ICMC / USP). Consultado em 18 de maio de 2017
- ↑ «Análise de Variância» (PDF). Universidade Federal do Rio Grande do Sul (UFRGS). Consultado em 18 de maio de 2017
- ↑ Loveland, Jennifer L. (2011). Mathematical Justification of Introductory Hypothesis Tests and Development of Reference Materials (M.Sc. (Mathematics)). Utah State University. Consultado em 30 de abril de 2013 Abstract: "The focus was on the Neyman–Pearson approach to hypothesis testing. A brief historical development of the Neyman–Pearson approach is followed by mathematical proofs of each of the hypothesis tests covered in the reference material." The proofs do not reference the concepts introduced by Neyman and Pearson, instead they show that traditional test statistics have the probability distributions ascribed to them, so that significance calculations assuming those distributions are correct. The thesis information is also posted at mathnstats.com as of April 2013.
- ↑ a b Weiss, Neil A. «Elementary statistics» (PDF). p. 1. Consultado em 5 de junho de 2017
- ↑ a b «Capítulo 10 Testes para duas amostras» (PDF). Universidade do Espírito Santo. p. 9. Consultado em 2 de junho de 2017
- ↑ a b Spiegel, Murray R. (2006). Estatística. São Paulo: Pearson. 284 páginas
- ↑ a b Magalhães, Marcos Nascimento; Lima, Antonio Carlos Pedroso de (2008). Noções de probabilidade e estatística. São Paulo: EdUSP. pp. 295 – 296
- ↑ a b Lopes, Aline Cristina Berbet; Leinioski, Amanda da Cruz; Ceccon, Larissa (2015). «Testes t para comparação de médias de dois grupos independentes» (PDF). UFPR. p. 11. Consultado em 2 de junho de 2017
- ↑ a b NIST handbook: Two-Sample t-test for Equal Means
- ↑ a b Zeghzeghi, M. I.; Cruz, F. R. B. (2010). «Teste de Significância via testes de Permutação na comparação de Médias em pequenas amostras» (PDF). Universidade Federal de Minas Gerais. p. 6. Consultado em 2 de junho de 2017
- ↑ a b REIS, MARCELO MENEZES. «TESTES DE HIPÓTESES» (PDF). UFSC. p. 24. Consultado em 2 de junho de 2017
- ↑ a b «Capítulo 10 Testes para duas amostras» (PDF). Universidade Federal do Espírito Santo. 2008. p. 36. Consultado em 5 de maio de 2017
- ↑ a b «Equivalence Tests for Two Proportions» (PDF). PASS Sample Size Software. p. 5. Consultado em 5 de junho de 2017
- ↑ a b «Test for variance or standard deviation» (PDF). p. 439. Consultado em 5 de junho de 2017
- ↑ a b Bolfarine, Heleno (2013). «- Testes Qui-quadrado - Aderência e Independência» (PDF). IMEUSP. p. 9. Consultado em 5 de junho de 2017
- ↑ Steel, R. G. D., and Torrie, J. H., Principles and Procedures of Statistics with Special Reference to the Biological Sciences., McGraw Hill, 1960, page 350.
- ↑ Weiss, Neil A. (1999). Introductory Statistics 5th ed. [S.l.: s.n.] 802 páginas. ISBN 0-201-59877-9
- ↑ a b Williams, Richard (13 de janeiro de 2015). «Review of Multiple Regression» (PDF). University of Notre Dame. p. 3. Consultado em 5 de junho de 2017
- ↑ NIST handbook: F-Test for Equality of Two Standard Deviations (Testing standard deviations the same as testing variances)
- ↑ Steel, R. G. D., and Torrie, J. H., Principles and Procedures of Statistics with Special Reference to the Biological Sciences., McGraw Hill, 1960, page 288.)
- ↑ a b Bussab, Wilton de O.; Morettin, Pedro A. (2010). Estatística Básica 6ª ed. [S.l.]: Saraiva. p. 339—340. 557 páginas
- ↑ a b c Bussab, Wilton de O.; Morettin, Pedro A. (2010). Estatística Básica 6ª ed. [S.l.]: Saraiva. p. 341—343. 557 páginas
- ↑ a b c d e f g h i j k l m n o p q r s t Lehmann, E. L.; Romano, Joseph P. (2005). Testing Statistical Hypotheses 3E ed. New York: Springer. ISBN 0-387-98864-5
- ↑ a b Ehlers, Ricardo S. (2003). «Introdução a Inferência Bayesiana - Distribuições a Priori». Universidade Federal do Paraná. p. 1. Consultado em 13 de abril de 2017
- ↑ Ash, Robert (1970). Basic probability theory. New York: Wiley. ISBN 978-0471034506Seção 8.2
- ↑ a b Tukey, John W. (1960). «Conclusions vs decisions». Technometrics. 26 (4): 423–433. doi:10.1080/00401706.1960.10489909 "Until we go through the accounts of testing hypotheses, separating [Neyman–Pearson] decision elements from [Fisher] conclusion elements, the intimate mixture of disparate elements will be a continual source of confusion." ... "There is a place for both "doing one's best" and "saying only what is certain," but it is important to know, in each instance, both which one is being done, and which one ought to be done."
- ↑ Queiroz, Marina Muniz de. «ESTATÍSTICA BAYESIANA» (PDF). UFMG. p. 2. Consultado em 30 de maio de 2017
- ↑ Stigler, Stephen M. (1996). «The History of Statistics in 1933». Statistical Science. 11 (3): 244–252. JSTOR 2246117. doi:10.1214/ss/1032280216
- ↑ Santos, Flávia Oliveira; Nicoletti, Maria do Carmo. «O Uso do Modelo de Bayes em Sistemas Baseados em Conhecimento». Universidade Federal de São Carlos. p. 8. Consultado em 13 de abril de 2017
- ↑ Lovric, Miodrag (18 de novembro de 2013). «On the diminishing of scientific methods based on p-values: Frequentist and Bayesian perspective» (PDF). UFPE. p. 1. Consultado em 30 de maio de 2017
- ↑ Berger, James O. (2003). «Could Fisher, Jeffreys and Neyman Have Agreed on Testing?». Statistical Science. 18 (1): 1–32. doi:10.1214/ss/1056397485
- ↑ a b Queiroz, Marina Muniz de. «ESTATÍSTICA BAYESIANA» (PDF). UFMG. p. 4. Consultado em 30 de maio de 2017
- ↑ «Probabilidades e Teoremas de BAYES». Universidade Estadual de Maringá. p. 1. Consultado em 30 de maio de 2017
- ↑ «Multiple Testing» (PDF). ETH Zurich. Consultado em 18 de maio de 2017
- ↑ Goeman, Jelle J.; Solari, Aldo (20 de maio de 2014). «Multiple Hypothesis Testing in Genomics». Statistics in Medicine. 33 (11): 1946 – 1978
- ↑ Laird, Nan M.; Lange, Christoph (2011). The Fundamentals of Modern Statistical Genetics. [S.l.]: Springer. p. 162. 222 páginas
- ↑ Aickin, M; Gensler, H (maio de 1996). «Adjusting for multiple testing when reporting research results: the Bonferroni vs Holm methods». Am J Public Health. 86 (5): 726–728. PMC 1380484
 . PMID 8629727. doi:10.2105/ajph.86.5.726
. PMID 8629727. doi:10.2105/ajph.86.5.726
- ↑ Mittelhammer, Ron C.; Judge, George G.; Miller, Douglas J. (2000). Econometric Foundations. [S.l.]: Cambridge University Press. pp. 73–74. ISBN 0-521-62394-4
- ↑ Miller, Rupert G. (1966). Simultaneous Statistical Inference. [S.l.]: Springer
- ↑ a b c d Casella, George; Berger, Roger L. (2002). Statistical Inference. [S.l.]: Duxbury. pp. 11–13. ISBN 0-534-24312-6
- ↑ Klaus, Dohmen (2003). Improved Bonferroni Inequalities via Abstract Tubes –Inequalities and Identities of Inclusion–Exclusion Type. Col: Lecture Notes in Mathematics. Berlim: Springer–Verlag Berlin Heidelberg. 122 páginas
- ↑ Haynes, Winston (2013). «Holm's Method». Springer New York. Encyclopedia of Systems Biology. 902 páginas
- ↑ Holm, S. (1979). «A simple sequentially rejective multiple test procedure». Scandinavian Journal of Statistics. 6 (2): 65–70. JSTOR 4615733. MR 538597
- ↑ Abdi, Hervé (2010). «Holm's Sequential Bonferroni Procedure» (PDF). Encyclopedia of Research Design
- ↑ «Bonferroni–Holm» (PDF). University of Ottawa. Consultado em 18 de maio de 2017
- ↑ Abdi, Hervé. «The Bonferonni and Šidák Corrections for Multiple Comparisons» (PDF)
- ↑ Morrison, Denton; Henkel, Ramon (2006) [1970]. The Significance Test Controversy. [S.l.]: AldineTransaction. ISBN 0-202-30879-0
- ↑ Oakes, Michael (1986). Statistical Inference: A Commentary for the Social and Behavioural Sciences. Chichester New York: Wiley. ISBN 0471104434
- ↑ Chow, Siu L. (1997). Statistical Significance: Rationale, Validity and Utility. [S.l.: s.n.] ISBN 0-7619-5205-5
- ↑ Harlow, Lisa L.; Mulaik, Stanley A.; Steiger, James H. (1997). What If There Were No Significance Tests?. [S.l.]: Lawrence Erlbaum Associates. ISBN 978-0-8058-2634-0
- ↑ a b Kline, Rex (2004). Beyond Significance Testing: Reforming Data Analysis Methods in Behavioral Research. Washington, D.C.: American Psychological Association. ISBN 9781591471189
- ↑ McCloskey, Deirdre N.; Ziliak, Stephen T. (2008). The Cult of Statistical Significance: How the Standard Error Costs Us Jobs, Justice, and Lives. [S.l.]: University of Michigan Press. ISBN 0-472-05007-9
- ↑ Cornfield, Jerome (1976). «Recent Methodological Contributions to Clinical Trials» (PDF). American Journal of Epidemiology. 104 (4): 408–421
- ↑ Yates, Frank (1951). «The Influence of Statistical Methods for Research Workers on the Development of the Science of Statistics». Journal of the American Statistical Association. 46: 19–34. doi:10.1080/01621459.1951.10500764 "The emphasis given to formal tests of significance throughout [R.A. Fisher's] Statistical Methods ... has caused scientific research workers to pay undue attention to the results of the tests of significance they perform on their data, particularly data derived from experiments, and too little to the estimates of the magnitude of the effects they are investigating." ... "The emphasis on tests of significance and the consideration of the results of each experiment in isolation, have had the unfortunate consequence that scientific workers have often regarded the execution of a test of significance on an experiment as the ultimate objective."
- ↑ Begg, Colin B.; Berlin, Jesse A. (1988). «Publication bias: a problem in interpreting medical data». Journal of the Royal Statistical Society, Series A: 419–463
- ↑ Meehl, Paul E. (1967). «Theory-Testing in Psychology and Physics: A Methodological Paradox» (PDF). Philosophy of Science. 34 (2): 103–115. doi:10.1086/288135. Consultado em 14 de junho de 2017. Arquivado do original (PDF) em 3 de dezembro de 2013 Thirty years later, Meehl acknowledged statistical significance theory to be mathematically sound while continuing to question the default choice of null hypothesis, blaming instead the "social scientists' poor understanding of the logical relation between theory and fact" in "The Problem Is Epistemology, Not Statistics: Replace Significance Tests by Confidence Intervals and Quantify Accuracy of Risky Numerical Predictions" (Chapter 14 in Harlow (1997)).
- ↑ Gigerenzer, G (2004). «Mindless statistics». The Journal of Socio-Economics. 33 (5): 587–606. doi:10.1016/j.socec.2004.09.033
- ↑ Nunnally, Jum (1960). «The place of statistics in psychology». Educational and Psychological Measurement. 20 (4): 641–650. doi:10.1177/001316446002000401
- ↑ Lykken, David T. (1991). «What's wrong with psychology, anyway?». Thinking Clearly About Psychology. 1: 3–39
- ↑ Luiz, Ronir Raggio; Struchiner, Claudio José (2002). «2. O Modelo Estatístico de Causalidade». Inferência Causal em Epidemiologia: O Modelo de Respostas Potenciais (PDF). Rio de Janeiro: FIOCRUZ. p. 29. 112 páginas
- ↑ «Conceitos Elementares de Estatística». Universidade Federal de Santa Catarina (UFSC). Consultado em 4 de maio de 2017
- ↑ a b Jacob Cohen (1994). «The Earth Is Round (p < .05)». American Psychologist. 49 (12): 997–1003. doi:10.1037/0003-066X.49.12.997 This paper lead to the review of statistical practices by the APA. Cohen was a member of the Task Force that did the review.
- ↑ a b c d Nickerson, Raymond S. (2000). «Null Hypothesis Significance Tests: A Review of an Old and Continuing Controversy». Psychological Methods. 5 (2): 241–301. PMID 10937333. doi:10.1037/1082-989X.5.2.241
- ↑ Branch, Mark (2014). «Malignant side effects of null hypothesis significance testing». Theory & Psychology. 24 (2): 256–277. doi:10.1177/0959354314525282
- ↑ a b Wilkinson, Leland (1999). «Statistical Methods in Psychology Journals; Guidelines and Explanations». American Psychologist. 54 (8): 594–604. doi:10.1037/0003-066X.54.8.594 "Hypothesis tests. It is hard to imagine a situation in which a dichotomous accept-reject decision is better than reporting an actual p value or, better still, a confidence interval." (p 599). The committee used the cautionary term "forbearance" in describing its decision against a ban of hypothesis testing in psychology reporting. (p 603)
- ↑ «ICMJE: Obligation to Publish Negative Studies». Consultado em 3 de setembro de 2012. Arquivado do original em 16 de julho de 2012.
Editors should seriously consider for publication any carefully done study of an important question, relevant to their readers, whether the results for the primary or any additional outcome are statistically significant. Failure to submit or publish findings because of lack of statistical significance is an important cause of publication bias.
- ↑ Journal of Articles in Support of the Null Hypothesis website: JASNH homepage. Volume 1 number 1 was published in 2002, and all articles are on psychology-related subjects.
- ↑ Armstrong, J. Scott (2007). «Significance tests harm progress in forecasting». International Journal of Forecasting. 23 (2): 321–327. doi:10.1016/j.ijforecast.2007.03.004
- ↑ a b E. L. Lehmann (1997). «Testing Statistical Hypotheses: The Story of a Book». Statistical Science. 12 (1): 48–52. doi:10.1214/ss/1029963261
- ↑ Kruschke, J K (9 de julho de 2012). «Bayesian Estimation Supersedes the T Test». Journal of Experimental Psychology: General. 142: 573–603. doi:10.1037/a0029146
- ↑ Kass, R. E. (1993). «Bayes factors and model uncertainty» (PDF). Department of Statistics, University of Washington
- ↑ Rozeboom, William W (1960). «The fallacy of the null-hypothesis significance test» (PDF). Psychological Bulletin. 57 (5): 416–428. doi:10.1037/h0042040 "...the proper application of statistics to scientific inference is irrevocably committed to extensive consideration of inverse [AKA Bayesian] probabilities..."It was acknowledged, with regret, that a priori probability distributions were available "only as a subjective feel, differing from one person to the next" "in the more immediate future, at least".
- ↑ Berger, James (2006). «The Case for Objective Bayesian Analysis». Bayesian Analysis. 1 (3): 385–402. doi:10.1214/06-ba115 In listing the competing definitions of "objective" Bayesian analysis, "A major goal of statistics (indeed science) is to find a completely coherent objective Bayesian methodology for learning from data." The author expressed the view that this goal "is not attainable".
- ↑ Aldrich, J (2008). «R. A. Fisher on Bayes and Bayes' theorem» (PDF). Bayesian Analysis. 3 (1): 161–170. doi:10.1214/08-BA306. Consultado em 14 de junho de 2017. Arquivado do original (PDF) em 6 de setembro de 2014
- ↑ Mayo, D. G.; Spanos, A. (2006). «Severe Testing as a Basic Concept in a Neyman–Pearson Philosophy of Induction». The British Journal for the Philosophy of Science. 57 (2): 323–357. doi:10.1093/bjps/axl003
- ↑ Mathematics > High School: Statistics & Probability > Introduction Arquivado em 2012-07-28 na Archive.today Common Core State Standards Initiative (relates to USA students)
- ↑ College Board Tests > AP: Subjects > Statistics The College Board (relates to USA students)
- ↑ Huff, Darrell (1993). How to lie with statistics. New York: Norton. p. 8. ISBN 0-393-31072-8'Métodos estatísticos e termos estatísticos são necessários ao reportar os dados massivos de tendências sociais e econômicas, condições de mercado, piscinas de opinião, censos. Mas sem escritores que usam palavras com honestidade e leitores que sabem o que elas significam, o resultado pode ser somente semântica sem sentido.'
- ↑ Snedecor, George W.; Cochran, William G. (1967). Statistical Methods 6 ed. Ames, Iowa: Iowa State University Press. p. 3 "...As ideias básicas em estatística nos assiste em pensar claramente sobre o problema, provendo alguma direção guia sobre as condições que devem ser satisfeitas se interferências sonoras são feitas, e nos permite detectar muitas interferências que não têm boa fundamentação lógica."
- ↑ Sotos, Ana Elisa Castro; Vanhoof, Stijn; Noortgate, Wim Van den; Onghena, Patrick (2007). «Students' Misconceptions of Statistical Inference: A Review of the Empirical Evidence from Research on Statistics Education». Educational Research Review. 2: 98–113. doi:10.1016/j.edurev.2007.04.001
- ↑ Moore, David S. (1997). «New Pedagogy and New Content: The Case of Statistics». International Statistical Review. 65: 123–165. doi:10.2307/1403333
- ↑ Hubbard, Raymond; Armstrong, J. Scott (2006). «Why We Don't Really Know What Statistical Significance Means: Implications for Educators» (PDF). Journal of Marketing Education. 28 (2): 114–120. doi:10.1177/0273475306288399. Arquivado do original em 18 de maio de 2006 Preprint
- ↑ Sotos, Ana Elisa Castro; Vanhoof, Stijn; Noortgate, Wim Van den; Onghena, Patrick (2009). «How Confident Are Students in Their Misconceptions about Hypothesis Tests?». Journal of Statistics Education. 17 (2)
- ↑ Gigerenzer, G. (2004). «The Null Ritual What You Always Wanted to Know About Significant Testing but Were Afraid to Ask». The SAGE Handbook of Quantitative Methodology for the Social Sciences (PDF). [S.l.: s.n.] pp. 391–408. doi:10.4135/9781412986311
Ligações externas[editar | editar código-fonte]
- Verification of statistical hypotheses. M.S. Nikulin (originator), Encyclopedia of Mathematics.
- MATTHEWS, Robert. Bayesian critique of statistics in health: The great health hoax, 1998.
- DALLAL, Gerard V. et al. The little handbook of statistical practice. Gerard V. Dallal, 1999.
- COHEN, Jacob. The earth is round (p<. 05): Rejoinder. 1995.
- MBAStats.net






























































































































































