Tetração

Torre de potência infinita

Em matemática, Tetração (também conhecida como hiper-4) é uma exponencial iterada, o primeiro hiper operador após a exponenciação. A palavra tetração foi cunhada pelo matemático inglês Rubem Louis Goodstein de tetra- (quatro) e iteração. Tetração é usada como notação para números muito grandes, mas tem poucas aplicações práticas, por isso só tem sido estudada em matemática pura.

Aqui são mostrados exemplos dos primeiros quatro hiper operadores, com tetração como o quarto:

1. Adição

   A primeira e mais simples operação.

2. Multiplicação

   $a\times n=\underbrace {a+a+\cdots +a} _{n}$

   Geralmente também é uma das operações primárias, mas em casos especiais (para os números naturais) pode ser vista como a somado a si mesmo, n vezes.

3. Exponenciação

   $a^{n}=\underbrace {a\times a\times \cdots \times a} _{n}$

   a multiplicado por si mesmo, n vezes.

4. Tetração

   ${^{n}a}=\underbrace {a^{a^{\cdot ^{\cdot ^{a}}}}} _{n}$

   a exponenciado por si mesmo, n vezes.

Onde cada operação é definida pela iteração do anterior. A peculiaridade da tetração entre essas operações é que as três primeiras (adição, multiplicação e exponenciação) são generalizadas para os valores complexos de n, enquanto que para a tetração, nenhuma generalização regular foi ainda estabelecida; e a tetração não é considerada uma função elementar.

Adição (a + n) é a operação mais básica. A multiplicação (an) é também uma operação primária, embora para números naturais possa ser pensada como uma adição encadeada envolvendo n números a; e a exponenciação ($a^{n}$) pode ser pensada como uma multiplicação encadeada envolvendo n números a. Analogamente, tetração ($^{n}a$) pode ser pensada como uma potência encadeada envolvendo n números a. O parâmetro a pode ser chamado de parâmetro-base a ser seguido, enquanto o parâmetro n a ser seguido pode ser chamado de parâmetro-altura (que é inteiro na primeira abordagem, mas pode ser generalizado para altura fracionária, real e complexa).

Definição

Para qualquer número real positivo $a>0$ e inteiro não-negativo $n\geq 0$, definimos $\,\!{^{n}a}$ por:

• $\,\!{^{n}a}=1$ (se $n=0$) e
• $\,\!{^{n}a}=a^{(^{n-1}a)}$ (se $n>0$)

Potências iteradas

Como podemos ver a partir da definição, quando é avaliada uma tetração em uma "torre de exponenciação", a exponenciação é feita no mais profundo nível primário (na notação, no nível mais alto). Em outras palavras:$\,\!\ ^{4}2=2^{2^{2^{2}}}=2^{\left(2^{\left(2^{2}\right)}\right)}=2^{\left(2^{4}\right)}=2^{16}=65.536$

Nota-se que a exponenciação não é associativa, de modo que, avaliando a expressão em outra ordem, levará a uma resposta diferente:

$\,\!2^{2^{2^{2}}}\neq \left({\left(2^{2}\right)}^{2}\right)^{2}=2^{2\cdot 2\cdot 2}=2^{8}=256$

Assim, as torres exponenciais devem ser avaliadas a partir de cima para baixo (ou da direita para a esquerda). Programadores referem-se a esta escolha como associativa à direita.

Terminologia

Existem muitos termos para tetração, cada qual tem alguma lógica por trás disso, mas alguns não se tornaram usados por uma razão ou outra. Aqui está uma comparação de cada termo, com suas razões e contra-razões.

• O termo tetração (tetration), introduzido por Goodstein em seu artigo de 1947 Transfinite Ordinals in Recursive Number Theory (generalizando a representação-base recursiva usada no teorema de Goodstein para uso de altas operações), ganhou uma posição dominante. Também foi popularizado por Rudy Rucker em Infinity and the Mind.
• O termo "superexponenciação" foi publicado por Bromer em seu artigo Superexponentiation em 1987. Foi utilizado anteriormente por Ed Nelson, em seu livro Predicative Arithmetic, em Princeton University Press, em 1986.
• O termo hiperpotência é uma combinação natural de hiper e potência, que descreve adequadamente a tetração. O problema reside no significado de hiper em relação a hierarquia de hiper operadores. Ao considerar os hiper operadores, o termo hiper refere-se a todas as categorias; e a expressão super refere-se ao rank 4, ou tetração. Assim, sob estas considerações, o termo hiperpotência é enganoso, uma vez que este apenas se refere à tetração.
• O termo torre de potência é utilizado ocasionalmente, sob a forma "a torre de potência de ordem n", para ${\ \atop {\ }}{{\underbrace {a^{a^{\cdot ^{\cdot ^{a}}}}} } \atop n}$

Tetração é muitas vezes confundida com funções intimamente relacionadas e expressões. Isso ocorre porque grande parte da terminologia que é usada com elas pode ser usado com tetração. Aqui estão alguns termos relacionados:

Forma	Terminologia
$a^{a^{\cdot ^{\cdot ^{a^{a}}}}}$	Tetração
$a^{a^{\cdot ^{\cdot ^{a^{x}}}}}$	Exponenciais iteradas
$a_{1}^{a_{2}^{\cdot ^{\cdot ^{a_{n}}}}}$	Exponenciais aninhadas (também torres)
$a_{1}^{a_{2}^{a_{3}^{\cdot ^{\cdot ^{\cdot }}}}}$	Exponenciais infinitas (também torres)

Nas duas primeiras expressões, a é a base; e o número de vezes que aparece a é a altura (para adicionar um x). Na terceira expressão, n é a altura, mas cada uma das bases é diferente.

Cuidados devem ser tomados ao se referir a exponenciais iteradas, como é comum chamar expressões dessas formas de exponenciação iterada, que é ambígua, pois isso pode significar função iterada, potência ou exponencial iterada.

Notação

As notações em que a tetração pode ser escrita (algumas das quais permitem mesmo níveis mais elevados de iteração) incluem:

Nome	Forma	Descrição
Notação padrão	$\,{}^{n}a$	Usada por Maurer (1901) e Goodstein (1947); O livro de Rudy Rucker Infinity and the Mind popularizou a notação.
Notação de Knuth	$a{\uparrow \uparrow }n$	Permite extensão, ao colocar mais setas; ou, de forma ainda mais poderosa, uma seta indexada.
Notação de seta encadeada de Conway	$a\rightarrow n\rightarrow 2$	Permite a extensão pelo aumento do número 2 (equivalente com as extensões acima); mas também, ainda mais poderosa, pela extensão da cadeia
Função de Ackermann	${}^{n}2=\operatorname {A} (4,n-3)+3$	Permite que o caso especial $a=2$ possa ser escrito em termos da função de Ackermann.
Notação da exponencial iterada	${}^{n}a=\exp _{a}^{n}(1)$	Permite uma simples extensão a exponenciais iteradas a partir de valores iniciais diferentes de 1.
Notação de Hooshmand	$\operatorname {uxp} _{a}n,\,a^{\frac {n}{}}$
Notação de hiper operador	$a^{(4)}n,\,\operatorname {hyper} _{4}(a,n)$	Permite a extensão ao aumentar o número 4; o que resulta na família de Hiperoperações.
Notação ASCII	a^^n	Uma vez que a seta para cima é usada de forma idêntica ao acento circunflexo (^), o operador de tetração pode ser escrito como (^^).

Uma notação acima usa a notação exponencial iterada; em geral, esta é definida como segue:

$\exp _{a}^{n}(x)=a^{a^{\cdot ^{\cdot ^{a^{x}}}}}$ com n a's.

Não há muitas notações para exponenciais iteradas, mas aqui estão algumas:

Nome	Forma	Descrição
Notação padrão	$\exp _{a}^{n}(x)$	Euler cunhou a notação $\exp _{a}(x)=a^{x}$; e a notação de iteração $f^{n}(x)$ tem sido comum desde então.
Notação de Knuth	$(a{\uparrow })^{n}(x)$	Pode ser usada para superpotências e superexponenciais, aumentando-se o número de setas; usado no artigo sobre números muito grandes.
Notação de Ioannis Galidakis	$\,{}^{n}(a,x)$	Possível para grandes expressões na base.
ASCII (auxiliar)	a^^n@x	Baseada na visão de que uma exponencial iterada é uma tetração auxiliar.
ASCII (padrão)	exp_a^n(x)	Baseada na notação padrão.

Exemplos

Na tabela a seguir, a maioria dos valores são muito grandes para escrever em notação científica, de forma que a notação exponencial iterativa é utilizada para expressá-las em base 10. Os valores contendo um ponto decimal são aproximados.

$x$	${}^{2}x$	${}^{3}x$	${}^{4}x$
1	1	1	1
2	4	16	65,536
3	27	7,625,597,484,987	$\exp _{10}^{3}(1.09902)$
4	256	$\exp _{10}^{2}(2.18788)$	$\exp _{10}^{3}(2.18726)$
5	3,125	$\exp _{10}^{2}(3.33931)$	$\exp _{10}^{3}(3.33928)$
6	46,656	$\exp _{10}^{2}(4.55997)$	$\exp _{10}^{3}(4.55997)$
7	823,543	$\exp _{10}^{2}(5.84259)$	$\exp _{10}^{3}(5.84259)$
8	16,777,216	$\exp _{10}^{2}(7.18045)$	$\exp _{10}^{3}(7.18045)$
9	387,420,489	$\exp _{10}^{2}(8.56784)$	$\exp _{10}^{3}(8.56784)$
10	10,000,000,000	$\exp _{10}^{3}(1)$	$\exp _{10}^{4}(1)$

Extensões

Tetração pode ser estendida para definir ${^{n}0}$ e outros domínios de função também.

Extensão de base zero

O exponencial $0^{0}$ não é definido consistentemente. Assim, as tetrações $\,{^{n}0}$ não estão claramente definidas pela fórmula dada anteriormente. No entanto, $\lim _{x\rightarrow 0}{}^{n}x$ é bem definido; e existe:

$\lim _{x\rightarrow 0}{}^{n}x={\begin{cases}1,&n{\mbox{ par}}\\0,&n{\mbox{ ímpar}}\end{cases}}$

Assim, podemos definir de forma consistente ${}^{n}0=\lim _{x\rightarrow 0}{}^{n}x$. Isso é equivalente à definição $0^{0}=1$.

Sob essa extensão, ${}^{0}0=1$, então a regra ${^{0}a}=1$ a partir da definição original ainda se mantém.

Extensão para bases complexas

Tetração por período

Tetração pela fuga

Uma vez que números complexos podem ser elevados a potências, a tetração pode ser aplicada às bases da forma $z=a+bi$, onde $i$ é a raiz quadrada de -1. Por exemplo, ${}^{n}z$ onde $z=i$, a tetração é conseguida usando-se o ramo principal do logaritmo natural; e usando-se a fórmula de Euler, obtemos a relação:

$i^{a+bi}=e^{{i\pi \over 2}(a+bi)}=e^{-{b\pi \over 2}}\left(\cos {a\pi \over 2}+i\sin {a\pi \over 2}\right)$

Isto sugere uma definição recursiva para ${}^{(n+1)}i=a'+b'i$, dado qualquer ${}^{n}i=a+bi$:

$a'=e^{-{b\pi \over 2}}\cos {a\pi \over 2}$

$b'=e^{-{b\pi \over 2}}\sin {a\pi \over 2}$

Os seguintes valores aproximados podem ser derivados:

${}^{n}i$	Valor aproximado
${}^{1}i=i$	i
${}^{2}i=i^{\left({}^{1}i\right)}$	$0.2079$
${}^{3}i=i^{\left({}^{2}i\right)}$	$0.9472+0.3208i$
${}^{4}i=i^{\left({}^{3}i\right)}$	$0.0501+0.6021i$
${}^{5}i=i^{\left({}^{4}i\right)}$	$0.3872+0.0305i$
${}^{6}i=i^{\left({}^{5}i\right)}$	$0.7823+0.5446i$
${}^{7}i=i^{\left({}^{6}i\right)}$	$0.1426+0.4005i$
${}^{8}i=i^{\left({}^{7}i\right)}$	$0.5198+0.1184i$
${}^{9}i=i^{\left({}^{8}i\right)}$	$0.5686+0.6051i$

Resolvendo a relação inversa como na seção anterior, retorna o esperado $\,{}^{0}i=1$ e $\,{}^{(-1)}i=0$, com valores negativos de n dando infinitos resultados sobre o eixo imaginário. Plotados no plano complexo, a sequência inteira espiraliza até o limite de $0.4383+0.3606i$, o que poderia ser interpretado como o valor onde n é infinito.

Tais sequências de tetração têm sido estudadas desde a época de Euler, mas são pouco conhecidas devido ao seu comportamento caótico. A maioria das pesquisas publicadas, historicamente, tem-se centrado sobre a convergência da função de torre de potências. A pesquisa atual tem se beneficiado muito com o advento de poderosos computadores com softwares de matemática fractal e matemática simbólica. Muito do que se sabe sobre tetração vem de conhecimentos gerais da dinâmica complexa e pesquisas específicas do mapa exponencial.

Extensão para alturas infinitas

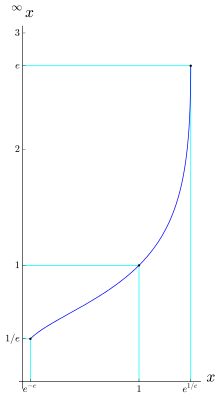
A tetração pode ser estendida para alturas infinitas (n em ${}^{n}a$). Isto porque, para bases dentro de um determinado intervalo, a tetração converge para um valor finito à medida que a altura tende a infinito. Por exemplo, ${\sqrt {2}}^{{\sqrt {2}}^{{\sqrt {2}}^{\cdot ^{\cdot ^{\cdot }}}}}$ converge para 2, e pode, portanto, ser considerada igual a 2. A tendência para o 2 pode ser vista pela avaliação de uma pequena torre finita:

${\begin{aligned}{\sqrt {2}}^{{\sqrt {2}}^{{\sqrt {2}}^{{\sqrt {2}}^{{\sqrt {2}}^{1.41}}}}}&={\sqrt {2}}^{{\sqrt {2}}^{{\sqrt {2}}^{{\sqrt {2}}^{1.63}}}}\\&={\sqrt {2}}^{{\sqrt {2}}^{{\sqrt {2}}^{1.76}}}={\sqrt {2}}^{{\sqrt {2}}^{1.84}}\\&={\sqrt {2}}^{1.89}=1.93\end{aligned}}$

Em geral, a torre de potência infinita $x^{x^{\cdot ^{\cdot ^{\cdot }}}}$, definida como o limite de ${}^{n}x$, tendo n indo ao infinito, converge para e^−e ≤ x ≤ e^1/e, aproximadamente o intervalo de 0.066 a 1.44, resultado mostrado por Leonhard Euler. O limite, se existir, é uma solução real positiva da equação y = x^y. Assim, x = y^1/y. O limite que define a tetração infinita de x falha em convergir para x > e^1/e porque o máximo de y^1/y é e^1/e.

Isso pode ser estendido para os números complexos z com a definição:

${}^{\infty }z=z^{z^{\cdot ^{\cdot ^{\cdot }}}}={\frac {\mathrm {W} (-\ln {z})}{-\ln {z}}}$

onde W(z) representa a Função de Lambert.

Como o limite y = ^∞x (se existente, ou seja, para e^−e < x < e^1/e) deve satisfazer x^y = y, vemos que x ↦ y = ^∞x é (o menor ramo) da função inversa de y ↦ x = y^1/y.

Extensão limitada às alturas negativas

A fim de preservar a regra original:

${^{(k+1)}a}=a^{({^{k}a})}$

Para valores negativos de $k$, devemos usar a relação recursiva:

${^{k}a}=\log _{a}\left({^{(k+1)}a}\right)$

Assim:

${}^{(-1)}a=\log _{a}\left({}^{0}a\right)=\log _{a}1=0$

No entanto, valores negativos menores não podem ser bem definidos desta forma, porque

${}^{(-2)}a=\log _{a}\left({}^{-1}a\right)=\log _{a}0$

Que não está bem definido.

Note ainda que, para $n=1$, qualquer definição de $\,\!{^{(-1)}1}$ é consistente com a regra, porque

${^{0}1}=1=1^{n}$ para qualquer $\,\!n={^{(-1)}1}$.

Extensão às alturas reais

Neste momento, não há solução comumente aceita para o problema geral de estender a tetração aos valores reais ou complexos de $n$. Várias abordagens são mencionadas abaixo.

Em geral, o problema é encontrar, para qualquer real a > 0, uma função super-exponencial $\,f(x)={}^{x}a$, sobre os reais $x>-2$, que satisfaça:

• $\,{}^{(-1)}a=0$;
• $\,{}^{0}a=1$;
• $\,{}^{x}a=a^{\left({}^{(x-1)}a\right)}$, para todo real x > -1;
• A quarta exigência, que é normalmente uma das seguintes:
  • A exigência de continuidade (normalmente, apenas ${}^{x}a$ é contínua em ambas as variáveis para $x>0$);
  • A exigência de diferenciabilidade (pode ser uma, duas, k vezes ou infinitamente diferenciável em x);
  • A exigência de regularidade (implicando duas vezes diferenciável em x), que:

$\left({\frac {d^{2}}{dx^{2}}}f(x)>0\right)$ para toda $x>0$

A quarta exigência difere de autor para autor; e entre abordagens. Existem duas abordagens principais para estender a tetração às alturas reais: uma baseia-se na exigência de regularidade; e a outra é baseada na exigência de diferenciabilidade. Estas duas abordagens parecem ser tão diferentes que não podem ser conciliadas, pois elas produzem resultados inconsistentes uma com a outra.

Felizmente, uma solução que satisfaça um destes em um intervalo de "tamanho um" pode ser estendida para uma solução a todos os números reais positivos. Quando $\,{}^{x}a$ é definida para um intervalo de "comprimento um", a função toda segue facilmente para todos $x>-2$.

Aproximações polinomiais

Aproximação linear:

Uma aproximação linear (solução para a exigência de continuidade, aproximação, com a exigência de diferenciabilidade) é dada por:

${}^{x}a\approx {\begin{cases}\log _{a}({}^{(x+1)}a)&x\leq -1\\1+x&-1<x\leq 0\\a^{\left({}^{(x-1)}a\right)}&x>0\end{cases}}$

Assim:

Aproximação	Domínio
$\,{}^{x}a\approx x+1$	for $-1<x<0$
$\,{}^{x}a\approx a^{x}$	for $0<x<1$
$\,{}^{x}a\approx a^{a^{(x-1)}}$	for $1<x<2$

E assim por diante. No entanto, é apenas diferenciável em seções; em valores inteiros de x, a derivada é multiplicada por $\ln {a}$.

Exemplos:$\,{}^{(\pi /2)}e\approx 5.868...,\;{}^{-4.3}0.5\approx 4.03335...,\;$

$\lim _{n\rightarrow \infty }x^{\frac {n}{}}$ Torre de potência infinita.

Um teorema principal no artigo de Hooshmand diz: Seja $0<a\neq 1$. Se $f:(-2,+\infty )\rightarrow \mathbb {R}$ é contínua e satisfaz as condições:

• $f(x)=a^{f(x-1)}\;\;{\mbox{for all}}\;\;x>-1,\;f(0)=1$ ;
• $f$ é diferenciável em $(-1,0)$;

  $f^{\prime }$ é uma função não decrescente ou não crescente em $(-1,0)$;

• $f^{\prime }(0^{+})=(\ln a)f^{\prime }(0^{-}){\mbox{ or }}f^{\prime }(-1^{+})=f^{\prime }(0^{-})$.

então $f$ é unicamente determinada através da equação:

$\;\;\;f(x)=\exp _{a}^{[x]}(a^{(x)})=\exp _{a}^{[x+1]}((x))\;\;\;{\mbox{for all}}\;\;x>-2$,

onde $(x)=x-[x]$ denota a parte fracionária de x; e $\exp _{a}^{[x]}$ é a $[x]$-função iterada da função $\exp _{a}$.

A prova é que a segunda até a quarta condição implicam trivialmente que f é uma função linear em [-1, 0].

A aproximação linear para a função de tetração natural ${}^{x}e$ é continuamente diferenciável, mas a sua segunda derivada não existe em valores inteiros de seu argumento. Hooshmand derivou outro teorema de unicidade para ela, que afirma:

Se $f:(-2,+\infty )\rightarrow \mathbb {R}$ é uma função contínua que satisfaz:

• $f(x)=e^{f(x-1)}\;\;{\mbox{para toda}}\;\;x>-1,\;f(0)=1$ ;
• $f$ é convexa em $(-1,0)$;
• $f^{\prime }(0^{-})\leq f^{\prime }(0^{+})$.

então $f={\mbox{uxp}}$. (Aqui, $f={\mbox{uxp}}$ é o nome de Hooshmand para a aproximação linear à função tetração natural).

A prova é a mesma coisa de antes; a equação de recursão garante que $f^{\prime }(-1^{+})=f^{\prime }(0^{+})$; e, em seguida, a condição de convexidade implica que $f$ é linear em (-1, 0).

Portanto, a aproximação linear para tetração natural é a única solução da equação $f(x)=e^{f(x-1)}\;\;(x>-1)$ e $f(0)=1$, o que é convexo em $(-1,+\infty )$. Todas as outras soluções suficientemente diferenciáveis devem ter um ponto de inflexão no intervalo (-1, 0).

Aproximações de alta ordem:

Uma aproximação quadrática (à exigência da diferenciabilidade) é dada por: \log_a({}^{(x+1)}a) & x \le -1 \\ 1 + \frac{2\log(a)}{1+\log(a)}x - \frac{1-\log(a)}{1+\log(a)}x^2 & -1 < x \le 0 \\ a^{\left({}^{(x-1)}a\right)} & x > 0 \end{cases}</math>, que é diferenciável para todo $x>0$, mas não duas vezes diferenciável. Se $a=e$, então isso é o mesmo que a aproximação linear.

A aproximação cúbica e um método para a generalização das aproximações de grau n são dadas em.

Extensão para alturas complexas

Desenho da extensão analítica $f=F(x+{\rm {i}}y)$ de Tetração ao plano complexo. Níveis $|f|=1,e^{\pm 1},e^{\pm 2},\ldots$ e níveis $\arg(f)=0,\pm 1,\pm 2,\ldots$ são mostrados com curvas espessas.

Existe uma conjectura em que existe uma única função F, que é uma solução da equação F(z+1)=exp(F(z)); e satisfaz as condições adicionais em que F(0)=1 e F(z) se aproximam dos pontos fixos do logaritmo (aproximadamente 0.31813150520476413531 ± 1.33723570143068940890i) à medida que z se aproxima de ±i∞ e que F é holomorfa em todo o plano-z complexo, exceto a parte do eixo real em z ≤ −2. Esta função é mostrada na figura à direita.

A aproximação de precisão complexa dupla dessa função está disponível online.

A exigência de holomorfismo da tetração é importante para a singularidade. Muitas funções $S$ podem ser construídas como

$S(z)=F\!\left(~z~+\sum _{n=1}^{\infty }\sin(2\pi nz)~\alpha _{n}+\sum _{n=1}^{\infty }{\Big (}1-\cos(2\pi nz){\Big )}~\beta _{n}\right)$

Onde $\alpha$ e $\beta$ são sequências reais que se decompõem com rapidez suficiente para proporcionar a convergência da série, pelo menos em valores moderados de $\Im (z)$.

A função S satisfaz as equações da tetração S(z+1)=exp(S(z)), S(0)=1; e se α_n e β_n se aproxima de 0 rápido o suficiente, ela será analítica em uma vizinhança do eixo real positivo. No entanto, se alguns elementos de {α} ou {β} não são 0, então a função S tem uma multidão de singularidades adicionais e linhas de corte no plano complexo, devido ao crescimento exponencial do seno e cosseno ao longo do eixo imaginário; quanto menor o coeficiente {α} e {β} são, quanto mais longe estas singularidades são do eixo real.

A extensão da tetração no plano complexo é, portanto, essencial para a singularidade; e a tetração real-analítica não é única.

Funções inversas

As funções inversas das tetrações são frequentemente chamadas de super-raízes e super-logaritmos. A raiz super quadrada $\mathrm {ssrt} (x)$, que é a função inversa de $x^{x}$, pode ser representada com a Função W de Lambert:

$\mathrm {ssqrt} (x)=e^{W(\mathrm {ln} (x))}={\frac {\mathrm {ln} (x)}{W(\mathrm {ln} (x))}}$

Para cada inteiro n > 2, a função ⁿx é definida e crescente para x ≥ 1, eⁿ1 = 1, de modo que a n-ésima super-raiz de x existe para x ≥ 1.

No entanto, se a aproximação linear acima é usada, então ^yx = y + 1 se -1 ≤ y ≤ 0; então ^ysuper-raiz(y + 1) não pode existir.

Uma vez que uma definição crescente (em x) da tetração ^xa é selecionada, o correspondente super-logaritmo slog_a x é definido para todos os números reais x; e a > 1.

A função $\mathrm {slog} _{a}$ satisfaz:

$\mathrm {slog} _{a}{^{x}a}=x$

$\mathrm {slog} _{a}a^{x}=1+\mathrm {slog} _{a}x$

$\mathrm {slog} _{a}x=1+\mathrm {slog} _{a}\log _{a}x$

$\mathrm {slog} _{a}x>-2$

Ver também

• Função de Ackermann

Ligações externas

• Sítio sobre tetrações de Andrew Robbins
• Sítio sobre tetrações de Daniel Geisler
• Fórum de Tetrações