Algoritmo de Liu Hui para π

Parte de uma série de artigos sobre:
a constante matemática π
3.1415926535897932384626433...
Utilização
Área do círculo Circunferência Uso em outras fórmulas
Propriedades
Irracionalidade Transcendência
Valor
Menor que 22/7 Aproximações Memorização
Pessoas
Arquimedes Liu Hui Tsu Ch'ung Chih Ariabata Madhava Alcaxi Ludolph van Ceulen François Viète Seki Takakazu William Jones John Machin William Shanks Srinivāsa Rāmānujan John Wrench Yasumasa Kanada
História
Cronologia Livro
Na cultura
Projeto de lei de Indiana Dia do Pi
Tópicos relacionados
Quadratura do círculo Problema de Basileia Seis noves em pi

Método de Liu Hui para calcular a área de um círculo

O algoritmo de Liu Hui para π foi inventado por Liu Hui (fl. século III), um matemático do império de Cao Wei. Antes de sua época, a razão entre o perímetro de uma circunferência e seu diâmetro era muitas vezes tomada experimentalmente como três na China, enquanto Zhang Heng (78-139) a representava como sendo 3,1724 (da proporção do círculo celeste com o diâmetro da Terra, 92/29) ou como $\pi \approx {\sqrt {10}}\approx 3,162$. Liu Hui não ficou satisfeito com este valor. Ele comentou que ele era muito grande e ultrapassava a marca. Outro matemático, Wang Fan (228-266), forneceu $\pi \approx 142/45\approx 3,156$. Todos esses valores empíricos para π eram precisos para dois dígitos (ou seja, uma casa decimal). Liu Hui foi o primeiro matemático chinês a fornecer um algoritmo rigoroso para o cálculo de π para qualquer precisão. O próprio cálculo de Liu Hui com um polígono de 96 lados forneceu uma precisão de cinco dígitos: π ≈ 3,1416.

Liu Hui observou em seu comentário no Os nove capítulos da arte matemática, que a relação do perímetro de um hexágono inscrito com o diâmetro da circunferência era três, então π deve ser maior que três. Ele passou a fornecer uma descrição detalhada passo-a-passo de um algoritmo iterativo para calcular π com qualquer precisão estabelecida com base em bisseção de polígonos; ele calculou π entre 3,141024 e 3,142708 com um polígono de 96 lados; ele sugeriu que 3,14 era uma aproximação boa o suficiente, e expressou π como 157/50; ele admitiu que este número era um pouco pequeno. Inventou mais tarde um engenhoso método rápido para melhorá-lo, e obteve π ≈ 3,1416 com apenas um polígono de 96 lados, com uma precisão comparável à de um polígono de 1536 lados. Sua contribuição mais importante nessa área foi seu algoritmo simples iterativo para π.

Área de um círculo

A área no interior de um círculo é igual ao raio multiplicado por metade da circunferência, ou A = r x C/2 = r x r x π.

Liu Hui argumentou:

"Multiplique um lado de um hexágono pelo raio (de sua circunferência circunscrita), e então multiplique este resultado por três, para obter a área de um dodecágono; se cortarmos um hexágono em um dodecágono, multiplicarmos seu lado pelo seu raio e, novamente, multiplicarmos por seis, obtemos a área de um polígono de 24 lados; quanto mais fino cortamos, menor a perda em relação à área do círculo, portanto, com mais corte após corte, a área do polígono resultante coincidirá e se tornará uma com o círculo; não haverá perda".

Aparentemente, Liu Hui já havia dominado o conceito do limite

$\lim _{N\to \infty }$ área do polígono de $N$ lados = área do círculo.

Também, Liu Hui provou que a área de um círculo é metade de seu perímetro multiplicado por seu raio. Ele registrou:

"Entre um polígono e um círculo, há excesso de raio. Multiplique o excesso de raio por um lado do polígono. A área resultante excede o limite do círculo".

No diagrama d = excesso de raio. Multiplicando d por um lado resulta no oblongo ABCD que excede o limite do círculo. Se um lado do polígono é pequeno (i.e. existe um número muito grande de lados), então o excesso do raio é pequeno, então o excesso na área será pequeno.

Como visto no diagrama, quando N → ∞, d → 0, e ABCD → 0.

"Multiplique o lado de um polígono pelo seu raio, e a área duplica; portanto, multiplique metade do perímetro pelo raio para obter a área do círculo".

Quando N → ∞, metade do perímetro do polígono de N lados aproxima um semicírculo, assim metade do perímetro de um círculo multiplicada por seu raio é igual à área do círculo. Liu Hui não explicou em detalhes esta dedução. No entanto, é evidente usando o "princípio do complemento in-out" de Liu Hui, que ele forneceu nos nove capítulos sobre a arte matemática: recortar uma forma geométrica em partes, reorganizar as partes para formar outra forma, a área das duas formas serão idênticas.

Assim, rearranjando os seis triângulos verdes, três triângulos azuis e três triângulos vermelhos em um retângulo com largura = 3L e altura R mostra que a área do dodecágono = 3RL.

Em geral, multiplicar metade do perímetro de um N-polígono pelo seu raio produz a área de um 2N-polígono. Liu Hui usou este resultado repetidamente em seu algoritmo π.

Desigualdade π de Liu Hui

Desigualdade π de Liu Hui

Liu Hui provou uma desigualdade envolvendo π considerando a área de polígonos inscritos com lados N e 2N.

No diagrama, a área amarela representa a área de um N-polígono, denotada por $A_{N}$, e a área amarela mais a área verde representa a área de um 2N-polígono, denotada por $A_{2N}$. Portanto, a área verde representa a diferença entre as áreas do 2 N-polígono e do N-polígono:

$D_{2N}=A_{2N}-A_{N}.$

A área vermelha é igual à área verde, e assim também é $D_{2N}$. Então

área amarela + área verde + área vermelha = $A_{2N}+D_{2N}.$

Seja $A_{C}$ a área do círculo. Então

$A_{2N}<A_{C}<A_{2N}+D_{2N}.$

Se o raio da circunferência é assumido ser 1, então obtemos a desigualdade de Liu Hui:

$A_{2N}<\pi <A_{2N}+D_{2N}.$

Algoritmo iterativo

Algoritmo de Liu Hui para π

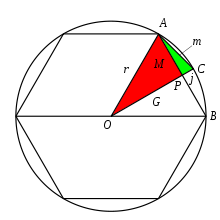
Liu Hui começou com um hexágono inscrito. Seja M o comprimento de um lado AB do hexágono, r o raio do círculo.

Bisseccionando AB com a linha OPC, AC torna-se um lado do dodecágono (12-polígono), seja seu comprimento m. Seja o comprimento de PC j e o comprimento de OP G.

AOP, APC são dois triângulos retângulos. Liu Hui usou o teorema de Gou Gu repetitivamente:

${}G^{2}=r^{2}-\left({\tfrac {M}{2}}\right)^{2}$

${}G={\sqrt {r^{2}-{\tfrac {M^{2}}{4}}}}$

${}j=r-G=r-{\sqrt {r^{2}-{\tfrac {M^{2}}{4}}}}$

${}m^{2}=\left({\tfrac {M}{2}}\right)^{2}+j^{2}$

${}m={\sqrt {\left({\tfrac {M}{2}}\right)^{2}+j^{2}}}$

${}m={\sqrt {\left({\tfrac {M}{2}}\right)^{2}+\left(r-G\right)^{2}}}$

${}m={\sqrt {\left({\tfrac {M}{2}}\right)^{2}+\left(r-{\sqrt {r^{2}-{\tfrac {M^{2}}{4}}}}\right)^{2}}}$

A partir daqui, existe agora uma técnica para determinar m de M, que dá o comprimento do lado de um polígono com o dobro do número de arestas. Começando com um hexágono, Liu Hui pode determinar o comprimento lateral de um dodecágono usando esta fórmula. Então continue repetidamente para determinar o comprimento lateral de um 24-polígono, dado o comprimento lateral de um dodecágono. Ele poderia fazer isso de forma recursiva quantas vezes fosse necessário. Sabendo como determinar a área destes polígonos, Liu Hui poderia então aproximar π.

Com $r=10$ unidades, ele obteve

área do 48-polígono ${}A_{96}=313{584 \over 625}$

área do 96-polígono ${}A_{192}=314{64 \over 625}$

Diferença do 96-polígono e do 48-polígono:

${}D_{192}=314{\frac {64}{625}}-313{\frac {584}{625}}={\frac {105}{625}}$

da desigualdade de Liu Hui para π:

$A_{2N}<A_{C}<A_{2N}+D_{2N}.$

Como r = 10, $A_{C}=100\times \pi$

então:

${}314{\frac {64}{625}}<100\times \pi <314{\frac {64}{625}}+{\frac {105}{625}}$

${}314{\frac {64}{625}}<100\times \pi <314{\frac {169}{625}}$

${}3,141024<\pi <3,142704.$

Ele nunca considerou π como a média do limite inferior 3,141024 e do limite superior 3,142704. Ao invés sugeriu que 3,14 era um valor aproximado bom o suficiente para π, e o expressou como a fração ${\tfrac {157}{50}}$; salientou que este número era ligeiramente menor que o exato.

Liu Hui efetuou seus cálculos com o sistema numérico de varas, e expressou os resultados com frações. Contudo, a natureza iterativa do algoritmo de Liu Hui para π é muito clara:

$2-m^{2}={\sqrt {2+(2-M^{2})}}\,,$

onde m é o comprimento de um lado do polígono de próxima ordem bissectado de M. O mesmo cálculo é feito repetidamente, cada passo requerendo somente uma adição e uma extração de raiz quadrada.

Método rápido

O cálculo de raízes quadradas de números irracionais não era uma tarefa fácil no século III com o sistema numérico de varas. Liu Hui descobriu um atalho comparando os diferenciais de área de polígonos, e constatou que a proporção da diferença na área de polígonos de ordem sucessiva era de aproximadamente 1/4.

Seja D_N a diferença de áreas de um N-polígono e um (N/2)-polígono

$D_{N}=A_{N}-A_{N/2}\,$.

Ele encontrou:

$D_{96}\approx {\tfrac {1}{4}}D_{48}$

$D_{192}\approx {\tfrac {1}{4}}D_{96}$

Então:

${\begin{aligned}D_{384}&{}\approx {\tfrac {1}{4}}D_{192}\\D_{768}&{}\approx \left({\tfrac {1}{4}}\right)^{2}D_{192}\\D_{1536}&{}\approx \left({\tfrac {1}{4}}\right)^{3}D_{192}\\D_{3072}&{}\approx \left({\tfrac {1}{4}}\right)^{4}D_{192}\\&{}\ \ \vdots \end{aligned}}$

Área do círculo de raio unitário =

${}\pi =A_{192}+D_{384}+D_{768}+D_{1536}+D_{3072}+\cdots \approx A_{192}+F\cdot D_{192}.\,$

Em que

$F={\tfrac {1}{4}}+\left({\tfrac {1}{4}}\right)^{2}+\left({\tfrac {1}{4}}\right)^{3}+\left({\tfrac {1}{4}}\right)^{4}+\cdots ={\frac {\frac {1}{4}}{1-{\frac {1}{4}}}}={\tfrac {1}{3}}.$

Isso é tudo o que subsequentes áreas em excesso somam a um terço de $D_{192}$

área do círculo unitário${}=\pi \approx A_{192}+\left({\tfrac {1}{3}}\right)D_{192}\approx {3927 \over 1250}\approx 3,1416.\,$

Ver também

• Método da exaustão
• Algoritmo de Zhao Youqin para π

Notas

↑1 Valor correto: 0.2502009052

↑2 Valor correto:

$A_{192}=3,1410319509$

$D_{192}=0,0016817478$

$\pi \approx A_{192}+{\frac {1}{3}}D_{192}\approxeq 3,1410319509+0,0016817478/3$

$\pi \approx 3,1410319509+0,0005605826$

$\pi \approx 3,1415925335.$

O método rápido de Liu Hui era potencialmente hábil para fornecer aproximadamente o mesmo resultado de um 12288-polígono (3,141592516588) com apenas um 96-polígono.

Leitura adicional

• Needham, Joseph (1986). Science and Civilization in China: Volume 3, Mathematics and the Sciences of the Heavens and the Earth. Taipei: Caves Books, Ltd.
• Wu Wenjun ed, History of Chinese Mathematics Vol III (em chinês) ISBN 7-303-04557-0