Espirógrafo

 Nota: Se procura gênero de poliquetas, veja Spirographis.

Alguns espirógrafos desenhados com um conjunto Spirograph

Evolução de uma típica Construção no Espirógrafo

Espirógrafo, um brinquedo produzido e vendido na União Soviética em 1980

Animation of a Spirograph

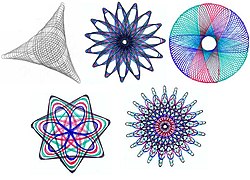
Espirógrafo é um produto registrado da Hasbro, Inc., um brinquedo para desenho geométrico. O espirógrafo produz curvas matemáticas conhecidas como hipotroclóides e epitroclóides. O termo tem sido usado para descrever várias aplicações de software que mostram curvas similares.

História

O espirógrafo foi inventado pelo engenheiro britânico Danys Fisher que exibiu-o em 1965 na Feira Internacional de Brinquedos de Nuremberg (Nuremberg International Toy Fair). Era produzido subsequentemente por sua empresa. Os direitos de distribuição foram adquiridos por Kenner, Inc., que introduziu-o no mercado dos Estados Unidos em 1966.

Funcionamento

Um espirógrafo consiste em um conjunto de engrenagens de plástico e outras formas como anéis, triângulos, ou barras retas. Existem vários tamanhos e formas de engrenagens, e todas as extremidades possuem dentes para se encaixar em outras peças. O ajuste das peças por exemplo, engrenagens pequenas dentro de anéis maiores. Mas também podem ser encaixados por fora dos anéis de forma a girarem ou na extremidade interna ou na extremidade externa dos anéis.

Para usá-lo, uma folha de papel é colocada sobre um papelão grosso, e uma das peças de plástico é fixada no papel e no papelão. Uma outra peça de plástico é encaixada de forma que seus dentes se encaixem com a peça fixada. Por exemplo, um anel pode ser fixado no papel e uma pequena engrenagem colocada dentro do anel - o atual número de arranjos possíveis por combinação de diferentes engrenagens é muito grande. A ponta de uma caneta é colocada em um dos buracos movendo a peça. Com a parte que se move, pelo rastro da caneta, é traçada a curva.

A caneta é usada tanto para desenhar quanto para promover a força locomotiva; é requerida alguma prática sobre Espirógrafo para poder operá-lo através das peças fixas e móveis. Mais complicados e formatos incomuns podem ser feitos com o uso de ambas as mãos, uma para desenhar e outra para guiar a peça. É possível mover várias peças em relação a outras (por exemplo, o triângulo em torno do anel, com um círculo "que sobe" do anel sobre o triângulo), mas isto requer concentração ou até assistência de outro artista.

Base matemática

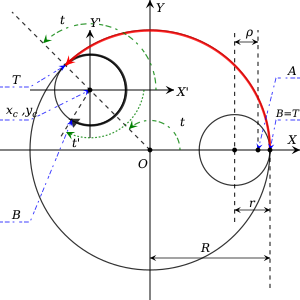
Consider um círculo externo fixo $C_{o}$ de raio $R$ centrado na origem. Um círculo menor interno $C_{i}$ de raio $r<R$ está rolando por dentro de $C_{o}$ e é continuamente tangente a ele. Será assumido que $C_{i}$ nunca derrapa em $C_{o}$ (em um Espirógrafo real, dentes em ambos círculos previnem tal derrapagem). Agora assuma que um ponto $A$ localizado em algum lugar dentro de $C_{i}$ está posicionado a uma distância $\rho <r$ do centro de $C_{i}$. Esse ponto $A$ corresponde ao buraco da caneta no disco interno de um Espirógrafo real. Sem perda de generalidade, pode-se supor que no momento inicial o ponto $A$ estava no eixo $X$. Para achar a trajetória criada por um Espirógrafo, siga o ponto $A$ assim que o círculo interno for posto em movimento.

Agora marque dois pontos $T$ em $C_{o}$ e $B$ em $C_{i}$. O ponto $T$ sempre indica onde os dois círculos são tangentes. Ponto $B$ entretanto vai mover-se em $C_{i}$ e a sua localização inicial coincide com $T$. Após pôr $C_{i}$ em movimento anti-horário em volta de $C_{o}$, $C_{i}$ tem uma rotação em sentido horário em relação ao seu centro. A distância que o ponto $B$ atravessa $C_{i}$ é a mesma que é atravessada pelo ponto tangente $T$ em $C_{o}$, devido à falta de derrapagem.

Agora defina o novo sistema de coordenadas (relativas) $(X',Y')$ com a sua origem no centro de $C_{i}$ e seus eixos paralelos a $X$ e $Y$. Admita o parâmetro $t$ como o ângulo em que o ponto tangente $T$ gira em $C_{o}$ e $t'$ seja o ângulo no qual $C_{i}$ gira (i.e. no qual $B$ percorre) no sistema relativo de coordenadas. Como não há derrapagem, as distâncias percorridas por $B$ e $T$ em seus respectivos círculos devem ser as mesmas, portanto $tR=(t-t')r$

ou equivalentemente

$t'=-{\frac {R-r}{r}}t.$

É comum assumir que um movimento anti-horário corresponde a uma mudança positiva do ângulo e um horário a uma mudança negativa. Um sinal negativo na fórmula acima ($t'<0$) acomoda essa convenção.

Admita $(x_{c},y_{c})$ serem as coordenadas do centro de $C_{i}$ no sistema de coordenadas absoluto. Então $R-r$ representa o raio da trajetória do centro de $C_{i}$, que (novamente no sistema de coordenadas absolutas) passa por movimento circular de:

${\begin{array}{rcl}x_{c}&=&(R-r)\cos t,\\y_{c}&=&(R-r)\sin t.\end{array}}$

Como definido acima, $t'$ é o ângulo de rotação no novo sistema relativo. Como o pontu $A$ obedece a lei usual de movimento circular, suas coordenadas no novo sistema de coordenadas relativas $(x',y')$ obedece:

${\begin{array}{rcl}x'&=&\rho \cos t',\\y'&=&\rho \sin t'.\end{array}}$

A fim de obter a trajetória de $A$ no (velho) sistema de coordenadas relativas, adicione esses dois movimentos:

${\begin{array}{rcrcl}x&=&x_{c}+x'&=&(R-r)\cos t+\rho \cos t',\\y&=&y_{c}+y'&=&(R-r)\sin t+\rho \sin t',\\\end{array}}$

onde $\rho$ é definido acima.

Agora, use a relação entre $t$ e $t'$ como derivado acima para obter equações descrevendo a trajetória do ponto $A$ em termos de um único parâmetro $t$:

${\begin{array}{rcrcl}x&=&x_{c}+x'&=&(R-r)\cos t+\rho \cos {\frac {R-r}{r}}t,\\[4pt]y&=&y_{c}+y'&=&(R-r)\sin t-\rho \sin {\frac {R-r}{r}}t.\\\end{array}}$

(usando o fato que a função $\sin$ é ímpar).

É conveniente representar a equação acima em termos do raio $R$ de $C_{o}$ e parâmetros adimensionais descrevendo a estrutura do Espirógrafo. Vamos admitir

$l={\frac {\rho }{r}}$

e

$k={\frac {r}{R}}.$

O parâmetro $0\leq l\leq 1$ representa o quão longe o ponto $A$ está localizado do centro de $C_{i}$. Ao mesmo tempo, $0\leq k\leq 1$ representa quão grande o círculo interno $C_{i}$ é em relação ao externo $C_{o}$.

Observa-se agora que

${\frac {\rho }{R}}=lk,$

e portanto as equações de trajetória ficam com a forma de

${\begin{array}{rcl}x(t)&=&R\left[(1-k)\cos t+lk\cos {\frac {1-k}{k}}t\right],\\[4pt]y(t)&=&R\left[(1-k)\sin t-lk\sin {\frac {1-k}{k}}t\right].\\\end{array}}$

Parâmetro $R$ é um parâmetro de escala e não afeta a estrutura do Espirógrafo. Diferentes valores de $R$ iriam produzir semelhantes desenhos de Espirógrafo.

Os dois casos extremos $k=0$ e $k=1$ resultam em trajetórias degeneradas do Espirógrafo. No primeiro caso extremo, quando $k=0$, temos um círculo simples de raio $R$, correspondente ao caso onde $C_{i}$ foi contraído a um ponto. (Divisão por $k=0$ na fórmula não é um problema uma vez que $\sin$ e $\cos$ são funções limitadas).

O outro caso extremo $k=1$ corresponde ao raio $r$ do círculo interno $C_{i}$ coincidindo com o raio $R$ do círculo externo $C_{o}$, i.e. $r=R$. Neste caso a trajetória é um simples ponto. Intuitivamente, $C_{i}$ é muito grande para rolar dentro do círculo de mesmo tamanho $C_{o}$ sem derrapar.

Se $l=1$, então o ponto $A$ está na circunferência de $C_{i}$. Nesse caso as trajetórias são chamadas de hipocicloides e as equções acima reduzidas àquelas para um hipocicloide.

Estrela

A empresa Estrela lançou um produto similar com o nome de "Espirograf".

Ver também

• Epicicloide

Bibliografia

• Knight, John I. (6 September 2018). "Mechanics Magazine". Knight; Lacey.
• Goldstein, Cathérine; Gray, Jeremy; Ritter, Jim (1996). L'Europe mathématique: histoires, mythes, identités. Editions MSH. p. 293.

Ligações externas

• «Spirograph in Java» 
• Weisstein, Eric W. «Spirograph» (em inglês). MathWorld 
• «Spirograph Toy Collection»  - Collection with photos of many versions including UK and Australian issues.
• «Software Spirograph»  in Javascript und AFLAX/Flash
• «Spirograph source files in C#» 
• https://collection.sciencemuseum.org.uk/objects/co60094/spirograph-and-examples-of-patterns-drawn-using-it-spirograph
• Kaveney, Wendy. "CONTENTdm Collection : Compound Object Viewer". http://digitallibrary.imcpl.org.
• Linderman, Jim. "ArtSlant - Spirograph? No, MAGIC PATTERN!". http://artslant.com.
• "From The Boy Mechanic (1913) - A Wondergraph". http://marcdatabase.com.