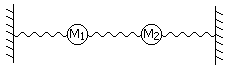Modo normal

Vários modos normais de uma rede unidimensional.

Um modo normal de um sistema oscilatório é a frequência na qual a estrutura deformável oscilará ao ser perturbada. Os modos normais são também chamados frequências naturais ou frequências ressonantes. Para cada estrutura existe um conjunto destas frequências que é único.

É usual utilizar um sistema formado por uma massa e uma mola para ilustrar o comportamento de uma estrutura deformável. Quando este tipo de sistema é excitado numa das suas frequências naturais, todas as massas movem-se com a mesma frequência. As fases das massas são exactamente as mesmas ou exactamente as contrárias. O significado prático pode ser ilustrado mediante um modelo de massa e mola de um edifício. Se um terremoto excita o sistema com uma frequência próxima a una das frequências naturais o deslocamento de um piso (nível) em relação a outro será máximo. Obviamente, os edifícios só podem suportar deslocamentos de até uma certa magnitude. Ser capaz de representar um edifício e encontrar os seus modos normais é uma forma fácil de verificar se o desenho do edifício é seguro. O conceito de modos normais também é aplicável em teoria ondulatória, óptica e mecânica quântica.

Exemplo - modos normais de osciladores acoplados

Sejam dois corpos (não afectados pela gravidade), cada um deles de massa M, vinculados a três molas com constante característica K. Os mesmos encontram-se vinculados da seguinte maneira:

onde os pontos em ambos os extremos estejam fixos e não se possam deslocar. Utiliza-se a variável x₁(t) para identificar o deslocamento da massa da esquerda, e x₂(t) para identificar o deslocamento da massa da direita.

Se tomar-se a derivada segunda de x(t) com respeito ao tempo como x″, as equações de movimentos são:

$Mx_{1}''=-K(x_{1})-K(x_{1}-x_{2})\,$

$Mx_{2}''=-K(x_{2})-K(x_{2}-x_{1})\,$

Prova-se uma solução do tipo:

$x_{1}(t)=A_{1}e^{i\omega t}\,$

$x_{2}(t)=A_{2}e^{i\omega t}\,$

Substituindo estas nas equação de movimento, obtém-se:

$-\omega ^{2}MA_{1}e^{i\omega t}=-2KA_{1}e^{i\omega t}+KA_{2}e^{i\omega t}\,$

$-\omega ^{2}MA_{2}e^{i\omega t}=KA_{1}e^{i\omega t}-2KA_{2}e^{i\omega t}\,$

dado que o factor exponencial é comum a todos os termos, pode-se omitir e simplificar a expressão:

$(\omega ^{2}M-2K)A_{1}+KA_{2}=0\,$

$KA_{1}+(\omega ^{2}M-2K)A_{2}=0\,$

O que em notação matricial é:

${\begin{bmatrix}\omega ^{2}M-2K&K\\K&\omega ^{2}M-2K\end{bmatrix}}{\begin{pmatrix}A_{1}\\A_{2}\end{pmatrix}}=0$

Para que esta equação não tenha uma solução não trivial, a matriz da esquerda deve ser singular, ou seja, o determinante da matriz deve ser igual a zero, portanto:

$(\omega ^{2}M-2K)^{2}-K^{2}=0\,$

Resolvendo para $\omega$, existem duas soluções:

$\omega _{1}={\sqrt {\frac {K}{M}}}$ \,

$\omega _{2}={\sqrt {\frac {3K}{M}}}$ \,

Se substitui-se $\omega _{1}$ na matriz e se resolve para ($A_{1},A_{2}$), obtem-se (1, 1). Se se substitui $\omega _{2}$, obtem-se (1, -1). (Estes vectores são autovectores, e as frequências denominam-se autovalores.)

O primeiro modo normal é:

${\begin{pmatrix}x_{1}(t)\\x_{2}(t)\end{pmatrix}}=c_{1}{\begin{pmatrix}1\\1\end{pmatrix}}\cos {(\omega _{1}t+\phi _{1})}$

e o segundo modo normal é:

${\begin{pmatrix}x_{1}(t)\\x_{2}(t)\end{pmatrix}}=c_{2}{\begin{pmatrix}1\\-1\end{pmatrix}}\cos {(\omega _{2}t+\phi _{2})}$

A solução geral é uma sobreposição dos modos normais onde c₁, c₂, φ₁, e φ₂, são determinados pelas condições iniciais do problema.

O processo demonstrado aqui pode ser generalizado utilizando o formalismo da mecânica lagrangiana ou mecânica hamiltoniana.

Ondas estacionárias

Uma onda estacionária é uma forma contínua de modo normal. Numa onda estacionária, todos os elementos do espaço (ou seja as coordenadas (x,y,z)) oscilam com a mesma frequência e em fase (alcançando o ponto de equilíbrio juntas), mas cada uma delas com uma amplitude diferente.

A forma general de uma onda estacionária é:

$\Psi (t)=f(x,y,z)(A\cos(\omega t)+B\sin(\omega t))$

onde f(x, y, z) representam a dependência da amplitude com a posição e o seno e coseno são as oscilações no decurso do tempo.

Onda estacionária gerada pela sobreposição de duas ondas viajantes. Observa-se a onda estacionária de cor negra, a onda de cor celeste desloca-se até à direita, enquanto que a onda de cor vermelha desloca-se até à esquerda. Em cada ponto e instante de tempo a onda negra obtem-se somando os valores de deslocamento nessa posição e esse instante de tempo.

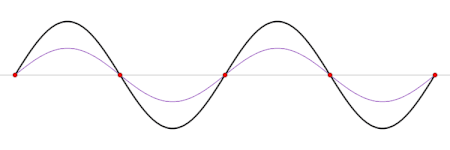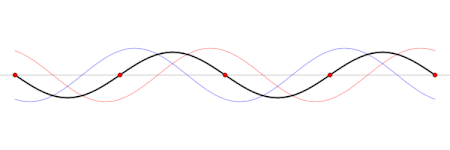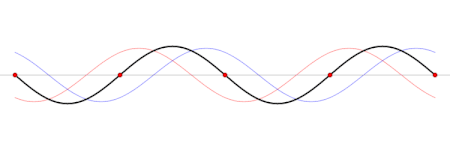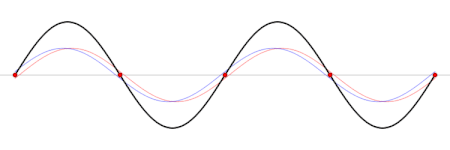
Em termos físicos, as ondas estacionárias são produzidas pela interferência (sobreposição) de ondas e suas reflexões (apesar de que também é possível dizer justamente o oposto; que uma onda viajante é uma sobreposição de ondas estacionárias). A forma geométrica do meio determina qual será o padrão de interferência, ou seja determina a forma f(x, y, z) da onda estacionária. Esta dependência no espaço é chamada um modo normal.

Usualmente, em problemas com dependência contínua de (x,y,z) não existe um número determinado de modos normais, em mudança existe um número infinito de modos normais. Se o problema está delimitado (ou seja está definido numa porção restringida do espaço) existe um número discreto infinito de modos normais (usualmente numerados n = 1,2,3,...). Se o problema não está delimitado, existe um espectro contínuo de modos normais.

As frequências permitidas dependem dos modos normais como também das constantes físicas do problema (densidade, tensão, pressão, etc.) o que determina a velocidade de fase da onda. A classe de todas as frequências normais é no geral chamado o espectro de frequências. De modo geral, cada frequência está modulada pela amplitude na qual foi gerado, dando lugar a um gráfico do espectro de potência das oscilações.

No âmbito da música, os modos normais de vibração dos instrumentos (cordas, sopro, percussão, etc.) são chamados "harmónicos".

Modos normais em mecânica quântica

Em mecânica quântica, o estado $\ |\psi \rangle$ de um sistema descreve-se pela sua função de onda $\ \psi (x,t)$, a qual é uma solução da equação de Schrödinger. O quadrado do valor absoluto de $\ \psi$ , ou seja:

$\ P(x,t)=|\psi (x,t)|^{2}$

é a densidade de probabilidade de medir a partícula na posição x no tempo t.

Usualmente, quando se relaciona com algum tipo de potencial, a função de onda descompõe-se na sobreposição de autovectores de energia definida, cada um oscilando com uma frequência $\omega =E_{n}/\hbar$. Portanto, pode-se expressar:

$|\psi (t)\rangle =\sum _{n}|n\rangle \left\langle n|\psi (t=0)\right\rangle e^{-iE_{n}t/\hbar }$

Os autovectores possuem um significado físico mais além da base ortonormal. Quando se mede a energia do sistema, a função de onda colapsa num de seus autovectores e portanto a função de onda da partícula descreve-se pelo autovector puro correspondente à energea medida.

Ver também

• tipos específicos:
  • Modo longitudinal
  • Modo transversal
• Aplicações físicas:
  • Ondas
  • Óptica
  • Oscilador harmónico
  • Espectroscopia vibracional
  • Teoria quântica
    • Equação de Schrödinger
    • Função de onda
    • Problema da medida
• Ferramentas matemáticas:
  • Álgebra linear
  • Equações diferenciais
  • Análise de Fourier
  • Teoria de Sturm-Liouville

Ligações externas

• «Java simulation of coupled oscillators» 
• Java simulation of the normal modes of a string, drum, and bar.