Parâmetro estatístico

Em estatística, um parâmetro é um número que resume a grande quantidade de dados que podem derivar do estudo de uma variável estatística.[1] O cálculo deste número está bem definido, usualmente mediante uma fórmula aritmética obtida a partir de dados da população.[2][3]
Os parâmetros estatísticos são uma consequência inevitável do propósito essencial da estatística: criar um modelo da realidade.[4]
O estudo de uma grande quantidade de dados individuais de uma população pode ser farragoso e inoperativo, pelo que se faz necessário realizar um resumo que permita ter uma ideia global da população, a comparar com outras, comprovar seu ajuste a um modelo ideal, realizar estimativas sobre dados desconhecidos da mesma e, em definitiva, tomar decisões. A estas tarefas contribuem de modo essencial os parâmetros estatísticos.
Por exemplo, costuma oferecer-se como resumo da juventude de uma população a média aritmética das idades de seus membros, isto é, a soma de todas elas, dividida pelo total de indivíduos que compõem tal população.
Enfoque descritivo[editar | editar código-fonte]

Um parâmetro estatístico é uma medida populacional. Este enfoque é o tradicional da estatística descritiva.[5][6][7] Neste sentido, sua acepção aproxima-se à de medida ou valor que se compara com outros, tomando uma unidade de uma determinada magnitude como referência.
Por sua vez, a fração mais formal da estatística, a estatística matemática e também a inferência estatística utilizam o conceito de parâmetro em seu aceitação matemática mais pura, isto é, como variável que define uma família de objetos matemáticos em determinados modelos. Assim se fala, por exemplo, de uma distribuição normal de parâmetros μ e σ como de uma determinada família de distribuições com uma distribuição de probabilidade de expressão conhecida, na que tais parâmetros definem aspectos concretos como a valor esperado, a variância, a curtose, etc. Outro exemplo comum neste sentido é o da distribuição de Poisson, determinada por um parâmetro, λ; ou a distribuição binomial, determinada por dois parâmetros, n e p. Desde o ponto de vista da estatística matemática, o facto de que estas distribuições descrevam situações reais e os citados parâmetros signifiquem um resumo de determinado conjunto de dados é indiferente.
Propriedades desejáveis num parâmetro[editar | editar código-fonte]
Segundo Yule[8] um parâmetro estatístico é desejável que tenha as seguintes propriedades:
- Define-se de maneira objetiva, isto é, é possível calculá-lo sem ambiguedades, geralmente mediante uma fórmula matemática. Por exemplo, a média aritmética define-se como a soma de todos os dados, dividida pelo número de dados. Não há ambiguedade: se realiza-se esse cálculo, obtém-se a média; se realiza-se outro cálculo, obtém-se outra coisa. No entanto, a definição de moda como o "valor mais frequente", pode dar lugar a confusão quando a maior frequência a apresentam vários valores diferentes.
- Não desperdiça, a priori, nenhuma das observações. Com carácter geral, um parâmetro será mais representativo de uma determinada população, quantos mais valores da variável estejam implicados em seu cálculo. Por exemplo, para medir a dispersão pode calcular-se o percurso, que só usa dois valores do variável objeto de estudo, os extremos; ou o desvio típico, em cujo cálculo intervêm todos os dados do eventual estudo.
- É interpretável, significa algo. Em média, por exemplo, deixa por abaixo de seu valor a metade dos dados, está justo no meio de todos eles quando estão ordenados. Esta é uma interpretação clara de seu significado.
- É singelo de calcular e presta-se com facilidade a manipulações algébricas. Ver-se-á mais abaixo que uma medida da dispersão é o desvio médio. No entanto, ao estar definida mediante um valor absoluto, função definida a troços e não deriváveis, não é útil para grande parte dos cálculos nos que estivesse implicada, ainda que sua interpretação seja muito clara.
- É pouco sensível às flutuações de amostras. Se pequenas variações numa amostra de dados estatísticos influem em grande parte num determinado parâmetro, é porque tal parâmetro não representa com confiabilidade a população. Por conseguinte é desejável que o valor de um parâmetro com esta propriedade se mantenha estável ante as pequenas oscilações que com frequência podem apresentar as diferentes amostras estatísticas. Esta propriedade é mais interessante no caso da estimativa de parâmetros. Por outra parte, os parâmetros que não variam com as mudanças de origem e escala ou cuja variação está controlada algebraicamente, são apropriados em determinadas circunstâncias como a tipificação.
Principais parâmetros[editar | editar código-fonte]
Habitualmente agrupam-se os parâmetros nas seguintes categorias:
- Medidas de posição.[9]
Trata-se de valores da variável estatística que se caracterizam pela posição que ocupam dentro da faixa de valores possíveis desta. Entre eles se distinguem:
- As medidas de tendência central: mediana, moda e média.
- As medidas de posição não central: quantias (quartiles, deciles e percentiles).
- Medidas de dispersão.[10]
Resumo da heterogeneidade dos dados, e separados que estes estão entre si. Há dois tipos, basicamente:
- Medidas de dispersão absolutas, que vêm dadas nas mesmas unidades nas que se mede a variável: percursos, desvios médios, variância, e desvio padrão.
- Medidas de dispersão relativa, que informam da dispersão em termos relativos, como uma percentagem. Incluem-se entre estas e o coeficiente de variação, o coeficiente de abertura, os percursos relativos e o índice de desvio respeito da média.
- Medidas de forma.[11]
Seu valor informa sobre o aspecto que tem a gráfica da distribuição. Entre elas estão os coeficientes de assimetria e os de curtoses.
- Outros parâmetros.
Alem desses, e com propósitos mais específicos, existem outros parâmetros de uso em situações muito concretas, como são as proporções, os números índice, as taxas e o coeficiente de Gini.
Medidas de tendência central ou centralização[editar | editar código-fonte]
São valores que costumam situar cerca do centro da distribuição de dados. Os mais destacados são as médias ou médias (incluindo a média aritmética, a média geométrica e a média harmônica), a média e a moda.
Média aritmética ou média[editar | editar código-fonte]

A média de amostras ou média aritmética é, provavelmente, um dos parâmetros estatísticos mais estendidos.[12] Suas propriedades são:[13]
- Seu cálculo é muito singelo e nele intervêm todos os dados.
- Interpreta-se como "equilíbrio mecânico" ou "centro de massas" do conjunto de dados, já que tem a propriedade de equilibrar os desvios dos dados respeito de seu próprio valor:
- Mininiza os desvios quadráticos dos dados respeito de qualquer valor prefixado, isto é, o valor de es mínimo cuando . Este resultado conhece-se como Teorema de König. Esta propriedade permite interpretar um dos parâmetros de dispersão mais importantes: a variança.
- Se vê afetada por transformações afins (mudanças de origem e escala), isto é, se
- entonces , donde es la media aritmética de los , para i = 1, ..., n e a e b números reais.
Este parâmetro, ainda tendo múltiplas propriedades que aconselham seu uso em situações muito diversas, tem também alguns inconvenientes, como são:
- Para dados agrupados em intervalos (variáveis contínuas), seu valor oscila em função da quantidade e amplitude dos intervalos que se considerem.
- É uma medida a cujo significado afecta sobremaneira a dispersão, de modo que quanto menos homogêneos são os dados, menos informação proporciona. Dito de outro modo, populações muito diferentes em sua composição podem ter a mesma média.[14] Por exemplo, uma equipa de basquetebol com cinco jogadores de igual estatura, 1,95, ponhamos por caso, teria uma estatura média de 1,95, evidentemente, valor que representa fielmente a esta homogênea população. No entanto, uma equipa de estaturas mais heterogéneas, 2,20, 2,15, 1,95, 1,75 e 1,70, por exemplo, teria também, como pode se comprovar, uma estatura média de 1,95, valor que não representa a quase nenhum de seus componentes.
- É muito sensível aos valores extremos da variável. Por exemplo, no cálculo do salário médio de uma empresa, o salário de um alto diretor que ganhe 1.000.000 de € tem tanto peso como o de mil empregados "normais" que ganhem 1.000 €, sendo a média de aproximadamente 2.000 €.
Moda[editar | editar código-fonte]
A moda é o dado mais repetido, o valor da variável com maior frequência absoluta.[15] Em verdadeiro sentido corresponde-se sua definição matemática com a locução "estar de moda", isto é, ser o que mais se leva.
Seu cálculo é extremamente singelo, pois só precisa de uma contagem. Em variáveis contínuas, expressadas em intervalos, existe o denominado intervalo modal ou, em seu defeito, se é necessário obter um valor concreto da variável, recorre-se à interpolação.
Suas principais propriedades são:
- Cálculo singelo.
- Interpretação muito clara.
- Ao depender só das frequências, pode se calcular para variáveis qualitativas. É por isso o parâmetro mais utilizado quando ao resumir uma população não é possível realizar outros cálculos, por exemplo, quando se listam em meios jornalísticos as características mais frequentes de determinado sector social. Isto se conhece informalmente como "retrato robô".[16]
Inconvenientes:
- Seu valor é independente da maior parte dos dados, o que a faz muito sensível a variações das amostras. Por outra parte, em variáveis agrupadas em intervalos, seu valor depende excessivamente do número de intervalos e de sua amplitude.
- Usa muito poucas observações, de tal modo que grandes variações nos dados fora da moda, não afectam em modo algum a seu valor.
- Não sempre se situa para o centro da distribuição.
- Pode ter mais de uma moda no caso em que dois ou mais valores da variável apresentem a mesma frequência (distribuições bimodais ou multimodais).
Média[editar | editar código-fonte]
A média é um valor da variável que deixa por embaixo de si à metade dos dados, uma vez que estes estão ordenados de menor a maior.[17] Por exemplo, a média do número de filhos de um conjunto de treze famílias, cujos respectivos filhos são: 3, 4, 2, 3, 2, 1, 1, 2, 1, 1, 2, 1 e 1, é 2, já que, uma vez ordenados os dados: 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 3, 3, 4, o que ocupa a posição central é 2:
Em caso de um número par de dados, a média não corresponderia a nenhum valor da variável, pelo que se convém em tomar como média o valor intermediário entre os dois valores centrais. Por exemplo, no caso de doze dados como os anteriores:
Toma-se como média

Existem métodos de cálculo mais rápidos para dados mais numerosos (veja-se o artigo principal dedicado a este parâmetro). Do mesmo modo, para valores agrupados em intervalos, acha-se o "intervalo médio" e, dentro deste, se obtém um valor concreto por interpolação.
Propriedades da média como parâmetro estatístico:[18]
- É menos sensível que a média a oscilações dos valores da variável. Um erro de transcrição na série do exemplo anterior em, ponhamos por caso, o último número, deixa à média inalterada.
- Como se comentou, pode se calcular para dados agrupados em intervalos, inclusive quando algum deles não está dimensionado.
- Não se vê afetada pela dispersão. De facto, é mais representativa que a média aritmética quando a população é bastante heterogénea. Costuma dar-se esta circunstância quando se resume a informação sobre os salários de um país ou uma empresa. Há uns poucos salários muito altos que elevam a média aritmética fazendo que perca representatividade com respeito ao grosso da população. No entanto, alguém com o salário "médio" saberia que há tanta gente que ganha mais dinheiro que ele, como que ganha menos.
Seus principais inconvenientes são que no caso de dados agrupados em intervalos, seu valor varia em função da amplitude destes. Por outra parte, não se presta a cálculos algébricos tão bem como a média aritmética.
Medidas de posição não central[editar | editar código-fonte]
Diretamente relacionados com a anterior, encontram-se as medidas de posição não central, também conhecidas como Quantiles. Trata-se de valores da variável estatística que deixam por abaixo de sim determinada quantidade dos dados. São, em definitiva, uma generalização do conceito da média. Enquanto esta deixa por abaixo de sim ao 50% da distribuição, os quantiles podem o fazer com qualquer outra percentagem.[19] Denominam-se medidas de posição porque informam, precisamente, da posição que ocupa um valor dentro da distribuição de dados.
Tradicionalmente distingue-se entre quartiles, se divide-se a quantidade de dados em quatro partes antes de proceder ao cálculo dos valores que ocupam cada posição; deciles, se divide-se os dados em dez partes; ou percentiles, que dividem a população em cem partes.
Exemplos: se diz-se que uma pessoa, depois de um teste de inteligência, ocupa o percentil 75, isso supõe que o 75% da população tem um quociente de inteligência com um valor inferior ao dessa pessoa. Este critério usa-se pelas associações de superdotados, que limitam seu conjunto de membros àquelas que atingem determinado percentil (igual ou superior a 98 na maioria dos casos).
O exemplo que se mostra na imagem da direita é o correspondente ao cálculo inverso, isto é, quando se deseja conhecer o percentil correspondente a um valor da variável, em lugar do valor que corresponde a um determinado percentil.
Outras medidas de posição central são a média geométrica e a média harmônica que, ainda que têm determinadas propriedades algébricas que poderiam as fazer úteis em determinadas circunstâncias, sua interpretação não é tão intuitiva como a dos parâmetros anteriores.
Comentários sobre as medidas de posição[editar | editar código-fonte]
Este tipo de parâmetros não têm por que coincidir com um valor exacto da variável e, por tanto, também não podem se usar com carácter geral para fazer prognósticos. Por exemplo, se diz-se que a média aritmética dos filhos das famílias de um país é de 1,2, não é possível encontrar famílias com esse valor mais especificamente. Um segundo exemplo: a nenhuma fábrica de sapatos ocorrer-se-lhe-ia fabricar os seus com talhas unicamente correspondentes ao valor média, nem sequer têm por que ser estas talhas as mais fabricadas, pois em tal caso seria mais apropriado atender à moda da distribuição de talhas dos eventuais clientes.
A eleição de um ou outro parâmetro dependerá de cada caso particular, dos valores da variável e dos propósitos do estudo. Seu uso indiscriminado pode ser deliberadamente tendencioso ou involuntariamente desviado, convertendo-se, de facto, num abuso.[20] Pode pensar-se, por exemplo, na seguinte situação: um empresário publica que o salário médio em sua empresa é de 1.600 €. A este dado, que em determinadas circunstâncias poderia se considerar muito bom, poderia se chegar se a empresa tivesse quatro empregados com salários de 1.000 € mensais e o salário do chefe, incluído na média, fosse de 4.000 € ao mês:[21]
Com carácter geral e a modo de resumo poderia dizer-se que a média aritmética é um parâmetro representativo quando a população segue uma distribuição normal ou é bastante homogênea; em outras situações de forte dispersão, teria que decantarse pela média. A moda é o último recurso (e o único) quando de descrever variáveis qualitativas se trata.
Medidas de dispersão[editar | editar código-fonte]

As medidas de posição resumem a distribuição de dados, mas resultam insuficientes e simplificam excessivamente a informação. Estas medidas adquirem verdadeiro significado quando vão acompanhadas de outras que informem sobre a heterogeneidade dos dados. Os parâmetros de dispersão medem isso precisamente, geralmente, calculando em que medida os dados se agrupam em torno de um valor central. Indicam, de um modo bem definido, o homogêneos que estes dados são. Há medidas de dispersão absolutas, entre as quais se encontram a variância, o desvio padrão ou o desvio absoluto, ainda que também existem outras menos utilizadas como os percursos ou a média; e medidas de dispersão relativas, como o coeficiente de variação, o coeficiente de abertura ou os percursos relativos. Em muitas ocasiões as medidas de dispersão oferecem-se acompanhando a um parâmetro de posição central para indicar em que medida os dados se agrupam em torno dele.[22]
Medidas de dispersão absolutas[editar | editar código-fonte]
Percursos[editar | editar código-fonte]
O percurso ou faixa de uma variável estatística é a diferença entre o maior e o menor valor que toma a mesma. É a medida de dispersão mais singela de calcular, ainda que é algo grossa porque só toma em consideração um par de observações. Basta apenas que um destes dois dados varie para que o parâmetro também o faça, ainda que o resto da distribuição siga sendo, essencialmente, a mesma.
Existem outros parâmetros dentro desta categoria, como os percursos ou faixas interquantílicos, que têm em conta mais dados e, por tanto, permitem afinar na dispersão. Entre os mais usados está a amplitude interquartil, que se define como a diferença entre o quartil terceiro e o quartil primeiro. Nessa faixa estão, pela própria definição dos quartiles, o 50% das observações. Este tipo de medidas também se usa para determinar valores atípicos. No diagrama de caixa que aparece à direita se marcam como valores atípicos todos aqueles que caem fora do intervalo [Li, Ls] = [Q1 - 1,5·Rs, Q3 + 1,5·Rs], onde Q1 e Q3 são os quartiles 1º e 3º, respetivamente, e Rs representa a metade do percurso ou faixa interquartílico, também conhecido como percorrido semiinterquartílico.[23]
Desvios médios[editar | editar código-fonte]
Dada uma variável estatístico X e um parâmetro de tendência central, c, chama-se desvio de um valor da variável, xi, respeito de c, ao número |xi - c|. Este número mede o comprimento que está cada dado do valor central c, pelo que uma média dessas medidas poderia resumir o conjunto de desvios de todos os dados.
Por conseguinte, denomina-se desvio médio da variável X respeito de c à média aritmética dos desvios dos valores do variável respeito de c, isto é, se
entonces
Deste modo definem-se desviação media a respeito da média (c = ) e a desviação média a respeito da média (c = ), cuja interpretação faz sentido em virtude do significado da média aritmética.[22]
No entanto, o uso de valores absolutos impede determinados cálculos algébricos que obrigam a eliminar estes parâmetros, apesar de sua clara interpretação, em favor dos seguintes.
Variança e desvio típico[editar | editar código-fonte]

Como se viu mais acima, a soma de todos os desvios com respeito ao parâmetro mais utilizado, a média aritmética, é zero. Por tanto se deseja-se uma medida da dispersão sem os inconvenientes para o cálculo que têm os desvios médios, uma solução é elevar ao quadrado tais desvios dantes de calcular a média. Assim, se define a varianza como:[24]
- ,
ou seja, a média dos quadrados dos desvios respeito da média.
O desvio típico, σ, define-se como a raiz quadrada da varianza, isto é,
Para variáveis agrupadas em intervalos, usam-se as marcas de classe (um valor apropriado do interior de cada intervalo) nestes cálculos.
Propriedades:[24]
- Ambos parâmetros não se alteram com as mudanças de origem.
- Se todos os valores da variável se multiplicam por uma constante, b, a varianza fica multiplicada por b2.
- No intervalo se encontram, pelo menos, o das observações (veja Desigualdade de Tchebyschev).[25]
Esta última propriedade mostra a potência do uso conjunto da média e o desvio típico como parâmetros estatísticos, já que para valores de k iguais a 2 e 3, respectivamente, se obtém que:
- No intervalo estão, pelo menos, os 75% dos dados.
- No intervalo estão, pelo menos, os 89% dos dados.
Cumpre-se a seguinte relação entre os parâmetros de dispersão:
onde , y são, respectivamente, o desvio médio respeito da média, o desvio médio respeito da média e o desvio típico (se veja desvio absoluto).
A média. É uma medida de dispersão que tem, por sua própria definição, as mesmas propriedades que a média. Por exemplo, não se vê afectada por valores extremos ou atípicos.[26]
Medidas de dispersão relativa[editar | editar código-fonte]
São parâmetros que medem a dispersão em termos relativos, uma percentagem ou uma proporção, por exemplo, de maneira que permitem uma singela comparação entre a dispersão de diferentes distribuições.[27]
Coeficiente de variação de Pearson[editar | editar código-fonte]
Define-se , onde o desvio típico e é a média aritmética.
Interpreta-se como o número de vezes que a média está contida no desvio típico. Costuma dar-se seu valor em tanto por cento, multiplicando o resultado anterior por 100. Deste modo obtém-se uma percentagem da variabilidad.
Seu principal inconveniente é que no caso de distribuições cuja média se acerca a zero, seu valor tende a infinito e inclusive resulta impossível de calcular quando a média é zero. Por isso não pode se usar para variáveis qualificadas.
Coeficiente de abertura[editar | editar código-fonte]
Se define como o cociente entre os valores extremos da distribução de dados, este é, dada una distribução de dados estatísticos x1, x2, ..., xn, seu coeficiente de abertura, CA é
Usa-se para comparar salários de empresas.
Percursos relativos[editar | editar código-fonte]
Dada uma distribução de dados estatísticos com quartiles Q1, Q2 e Q3, o recorrido interquartílico relativo, RIQR se define como[28]
Por outra parte, se define o recorrido semiinterquartílico relativo, RSIR, como
Índice de desvio com respeito à média[editar | editar código-fonte]
Se define como , onde DMe é a desviação média com respeito da mediana e Me é a mediana de uma distribução de dados estatísticos dada.
Medidas de forma[editar | editar código-fonte]

As medidas de forma caracterizam a forma da gráfica de uma distribuição de dados estatísticos. A maioria destes parâmetros tem um valor que costuma comparar com o sino de Gauss, isto é, a gráfica da distribuição normal, uma das que com mais frequência se ajusta a fenómenos reais.
Medidas de assimetria[editar | editar código-fonte]
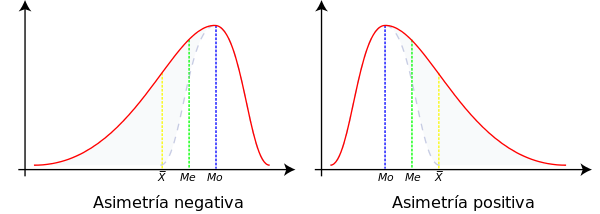
Diz-se que uma distribuição de dados estatísticos é simétrica quando a linha vertical que passa por sua média, divide a sua representação gráfica em duas partes simétricas. Isso equivale a dizer que os valores equidistantes da média, a um ou outro lado, apresentam a mesma frequência.
Nas distribuições simétricas os parâmetros média, média e moda coincidem, enquanto se uma distribuição apresenta certa assimetria, de um tipo ou de outro, os parâmetros se situam como mostra o seguinte gráfico:
Isso pode se demonstrar facilmente se se tem em conta a atração que a média aritmética sente pelos valores extremos, que já se comentou mais acima e as definições de média (justo no centro da distribuição, tomando o eixo de abscisas como referência) e moda (valor que apresenta uma ordenada mais alta).
Por conseguinte, a posição relativa dos parâmetros de centralização podem servir como uma primeira medida da simetria de uma distribuição.
Outras medidas mais precisas são o coeficiente de assimetria de Fisher, o coeficiente de assimetria de Bowley e o coeficiente de assimetria de Pearson.
Medidas de apontamento ou curtoses[editar | editar código-fonte]

Com estes parâmetros pretende-se medir como se repartem as frequências relativas dos dados entre o centro e os extremos, tomando como comparação o sino de Gauss.
O parâmetro usado com mais frequência para esta medida é o coeficiente de curtosis de Fisher, definido como:
- ,
ainda que há outros como o coeficiente de curtoses de Kelley ou o coeficiente de curtoses percentílico.
A comparação com a distribuição normal permite falar de distribuições platicúrticas ou mais aplastadas que a normal; distribuições mesocúrticas, com igual apuntamiento que a normal; e distribuições leptocúrticas, isto é, mais apontadas que a normal.[29]
Por último, existem outras medidas para decidir sobre a forma de uma distribuição com ajuste a modelos menos usuais como os que se mostram nas seguintes gráficas:
Outros parâmetros[editar | editar código-fonte]
Apresentam-se neste apartado outros parâmetros que têm aplicativo em situações muito concretas, pelo que não se incluem entre os grupos anteriores, ainda que têm cabida neste artigo por seu frequente uso em meios de comunicação e sua faculdade de resumir grandes quantidades de dados, como ocorre com as medidas tratadas até agora.
Proporção[editar | editar código-fonte]
A proporção de um dado estatístico é o número de vezes que se apresenta esse dado com respeito ao total de dados. Conhece-se também como frequência relativa e é um dos parâmetros de cálculo mais singelo. Tem a vantagem de que pode se calcular para variáveis qualitativas.
Por exemplo, se estuda-se a cor de olhos de um grupo de 20 pessoas, onde 7 delas os têm azuis, a proporção de indivíduos com olhos azuis é de 35% (= 7/20).
O dado com maior proporção conhece-se como moda (se veja, mais acima).
Em inferência estatística existem intervalos de confiança para a estimativa deste parâmetro.
Número índice[editar | editar código-fonte]
Um número índice é uma medida estatística que permite estudar as flutuações ou variações de uma magnitude ou a mais de uma em relação ao tempo ou ao espaço. Os índices mais habituais são os que realizam as comparações no tempo. Alguns exemplos de uso quotidiano deste parâmetro são o índice de preços ou o IPC[30]
Taxa[editar | editar código-fonte]
A taxa é um coeficiente que expressa a relação entre a quantidade e a frequência de um fenómeno ou um grupo de fenómenos. Utiliza-se para indicar a presença de uma situação que não pode ser medida em forma direta. Esta razão utiliza-se em âmbitos variados, como a demografia ou a economia, onde se faz referência à taxa de interesse.
Alguns dos mais usados são: taxa de natalidade, taxa de mortalidade, taxa de crescimento demográfico, taxa de fecundidade ou Desemprego.
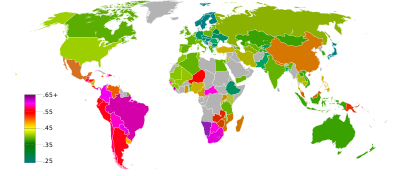
Coeficiente de Gini[editar | editar código-fonte]
O índice de Gini ou coeficiente de Gini é um parâmetro de dispersão usado para medir desigualdades entre os dados de uma variável ou a maior ou menor concentração dos mesmos.
Este coeficiente mede de que forma está distribuída a soma total dos valores da variável. Costuma-se usar para descrever salários. Os casos extremos de concentração seriam aquele nos que uma única pessoa toma o total do dinheiro disponível para salários e aquele no que este total está igualmente repartido entre todos os assalariados.[31]
Momentos[editar | editar código-fonte]
Os momentos são uma forma de generalizar toda a teoria relativa aos parâmetros estatísticos e guardam relação com uma boa parte deles. Dada uma distribuição de dados estatísticos x1, x2, ..., xn, se define o momento central o momento centrado de ordem k como
Para variáveis contínuas a definição muda somas discretas por integrais (soma contínua), ainda que a definição é, essencialmente, a mesma.[32] Desta definição e as propriedades dos parâmetros implicados que se viram mais acima, se deduze imediatamente que:
e que
Se chama momento não centrado de ordem k à seguinte expressão:
Da definição se deduz que:
Usando o binómio de Newton, pode obterse a seguinte relação entre os momentos centrados e não centrados:
Os momentos de uma distribuição estatística caracterizam-na univocamente.[34]
Parâmetros bidimensionais[editar | editar código-fonte]
Em estatística estudam-se em ocasiões várias características de uma população para compará-las, estudar sua dependência ou correlação ou realizar qualquer outro estudo conjunto. O caso mais comum de dois variáveis conhece-se como estatística bidimensional.[35]
Um exemplo típico é o de um estudo que recolha a estatura (a denotemos por X) e o peso (seja Y) dos n indivíduos de uma determinada população. Em tal caso, fruto da recolhida de dados, obtem-se uma série de pares de dados (xi, yi), com i = 1, ..., n, cada uma das quais estaria composta pelas estatura e o peso do individuo i, respectivamente.
Nos estudos bidimensionais, a cada uma das duas variáveis que entram em jogo, estudadas individualmente, podem resumir mediante os parâmetros que se viram até agora. Assim, faria sentido falar da média das estaturas () ou o desvio típico dos pesos (σY). Inclusive para um determinado valor da primeira variável, xk, cabe fazer estudos condicionados. Por exemplo, a média condicionada à estatura xk seria a média dos pesos de todos os indivíduos que têm essa estatura. Denota-se Me/x=xk.
No entanto existem outros parâmetros que resumem características de ambas distribuições em seu conjunto. Os mais destacados são o centro de gravidade, a covarianza e o coeficiente de correlação linear.
Centro de gravidade[editar | editar código-fonte]
Dadas dois variáveis X e Y, se define o centro de gravidade como o par (, ), onde e são, respectivamente, as médias aritméticas das variáveis X e Y.
O nome deste parâmetro prove/provem de que numa representação dos pares do estudo numa nuvem de pontos, na que cada ponto tivesse um peso proporcional a sua frequência absoluta, as coordenadas (, ) corresponderiam, precisamente, ao centro de gravidade como conceito físico.[36]
Covariança[editar | editar código-fonte]
A covariança ou variança conjunta de uma distribuição bidimensional define-se como:
A interpretação deste parâmetro tem que ver com a eventual correlação linear das duas variáveis. Uma covariança positiva implica uma correlação directa e uma negativa, uma correlação inversa.[37] Por outra parte, é um parâmetro imprescindível para o cálculo do coeficiente de correlação linear ou os coeficientes de regreção, como ver-se-á mais abaixo.
Em seu contra tem que se vê excessivamente influenciada, ao igual que ocorria com a média aritmética, pelos valores extremos das distribuições e as mudanças de escala.
Coeficiente de correlação linear[editar | editar código-fonte]

Trata-se de um coeficiente que permite determinar a bondade do ajuste da nuvem de pontos por uma recta.
Se define como: , onde σxy é a covariança e σx e σy, as desviações típicas respectivas das distribuções implicadas.
O coeficiente de correlação linear toma valores entre -1 e 1. Nessa escala, mede a correlação do seguinte modo:
- A correlação linear é mais forte quanto mais perto esteja de -1 ou 1.
- A correlação linear é mais débil quanto mais próximo de zero seja r.[38]
O diagrama da direita ilustra como pode variar r em função da nuvem de pontos associada:
Outros parâmetros bidimensionais são, o coeficiente de correlação de postos de Spearman, os coeficientes de correlação não paramétricos, o coeficiente de determinação ou os coeficientes de regreção linear.
Ao igual que com distribuições unidimensionales, existe uma forma equivalente de desenvolver a teoria relativa aos parâmetros estatísticos bidimensionais usando os momentos.
Os parâmetros na inferência estatística[editar | editar código-fonte]
Em ocasiões os parâmetros de uma determinada população não podem se conhecer com certeza. Geralmente isto ocorre porque é impossível o estudo da população completa por questões como que o processo seja destructivo (p.e., vida média de uma lâmpada) ou muito caro (p.e., audiências de televisão). Em tais situações recorre-se às técnicas da inferência estatística para realizar estimativas de tais parâmetros a partir dos valores obtidos de uma amostra da população.[39]
Distingue-se então entre parâmetros e estatísticos. Enquanto um parâmetro é uma função dos dados da população, o estatístico o é dos dados de uma amostra. Deste modo podem definir-se a média amostral, a variança amostral ou qualquer outro párametro dos mostrados mais acima.
Por exemplo, dada uma amostra estatística de tamanho n, , de uma variável aleatória X com distribuição de probabilidade F(x,θ), onde θ é um conjunto de parâmetros da distribuição, definir-se-ia a média amostral n-ésima como:
No caso concreto da variançaa amostral, costuma tomar-se, por suas melhores propriedades como estimador, a seguinte:
onde se tomou como denominador n-1, em lugar de n. A este parâmetro também se lhe chama quasivariança.[40]
Controvérsias e más interpretações[editar | editar código-fonte]
Como se disse, os parâmetros estatísticos, no enfoque descritivo que aqui se adopta, substituem grandes quantidades de dados por uns poucos valores extraídos daqueles através de operações simples. Durante este processo perde-se parte da informação oferecida originalmente por todos os dados. É por esta perda de dados pelo que a estatística tem sido chamada em ocasiões de uma falácia. Por exemplo, se num grupo de três pessoas uma delas ingere três gelados, o parâmetro que com mais frequência se utiliza para resumir dados estatísticos, a média aritmética do número de gelados ingeridos pelo grupo seria igual a 1 (), valor que não parece resumir fielmente a informação. Nenhuma das pessoas sentir-se-ia identificada com a frase resumo: "Tenho ingerido um gelado em média".[20]
Um exemplo menos conhecido mas igual de ilustrativo a respeito da clareza de um parâmetro é a distribuição exponencial, que costuma reger os tempos médios entre determinados tipos de acontecimentos. Por exemplo, se a vida média de um lâmpada é de 8.000 horas, mais do 50 por cento das vezes não chegará a essa média. Igualmente, se um autocarro passa a cada 10 minutos em media, há uma probabilidade maior de 50 por cento de que passe menos de 10 minutos entre um autocarro e o seguinte.
Outro exemplo que costuma se oferecer com frequência para argumentar na contramão da estatística e seus parâmetros é que, estatisticamente falando, a temperatura média de uma pessoa com os pés num forno e a cabeça numa geladeira é ideal.

Quiçá por situações como estas, que em geral mostram um profundo desconhecimento do que os parâmetros representam em realidade e de seu uso conjunto com outras medidas de centralização ou dispersão, o premiê britânico Benjamin Disraeli sentenciou primeiro e Mark Twain popularizou mais tarde a seguinte afirmação:
Existem mentiras, grandes mentiras, e estatísticas.— Benjamin Disraeli
Há outras personagens que também têm avisado sobre a simplificação que supõe a estatística, como o professor Aaron Levenstein, quem afirmava:
As estatísticas são como os biquinis: o que mostram são sugestivos, mas escondem o que é vital— Aaron Levenstein
Por sua vez, o escritor e comediante inglês Bernard Shaw sentenciou:
A estatística é uma ciência que demonstra que, se o meu vizinho tem duas carroças e eu nehuma, os dois temos uma.— George Bernard Shaw
ou a personagem fictícia Homer Simpson, da popular série de televisão Os Simpsons, numa entrevista a respeito das proporções num de seus capítulos:[41]
Oh!, a gente sai com estatísticas para provar qualquer coisa, os 14 porcento do mundo o sabe.— Guionistas da série Os Simpson
Ver também[editar | editar código-fonte]
- Desigualdade de Chebyshev, teorema que mostra a quantidade de dados que resumia conjuntamente a média aritmética e o desvio típico
- Diagrama de caixa, gráfico no que se apreciam visualmente as características de alguns dos parâmetros de centralização, posição e dispersão
- Estatística descritiva. A teoria estatística relativa aos parâmetros, tal e como se expuseram neste artigo, pertence a esta especialidade matemática
- Estatística robusta
- Estatístico, conceito equivalente ao de parâmetro quando se trata de uma amostra.
- Teoria da estimativa, diversos métodos para predizer o valor real de determinados parâmetros populacionais quando estes não podem se conhecer mediante experiências
- Intervalo de confiança, método para estimar o valor aproximado de um parâmetro estatístico
- Parâmetro, como objeto matemático
- Parâmetros mais comuns:
- Parâmetros de centralização:
- Parâmetros de dispersão:
- Medidas de posição não central:
- Outros parâmetros:
- Assimetria estatística,
- Coeficiente de Gini,
- Curtoses,
- Momento regular,
- Momento central,
- Número índice,
- Proporcionalidade,
- Taxa (índice);
- Parâmetros bidimensionais:
- População, como conceito estatístico.
- Regreção estatística
Referências
- ↑ Introducción a la Estadística. [S.l.: s.n.] p. 69. ISBN 8429150390
- ↑ «Parámetros estadísticos». Ditutor, Diccionario de Matemáticas
- ↑ Serret Moreno-Gil, Jaime. Procedimientos estadísticos. [S.l.: s.n.] p. 71. ISBN 8473561716
- ↑ Pascual, José; Galbiati, José; González, Gladys; Maulén, Mª Angélica; Arancibia, Rodrigo. Exploración de datos: Introducción a la Estadística Descriptiva. [S.l.: s.n.] Consultado em 16 de abril de 2009. Arquivado do original em 10 de abril de 2009
- ↑ «Parámetro estadístico». Enciclopedia Microsoft® Encarta® Online 2009. Microsoft Corporation. 2009. Consultado em 19 de abril de 2009. Cópia arquivada em 1 de abril de 2009.
Parámetro estadístico, número que se obtiene a partir de los datos de una distribución estadística y que sirve para sintetizar alguna característica relevante de la misma.
- ↑ Diccionario de Matemáticas. [S.l.: s.n.] p. 266. ISBN 84-89784-56-6.
Parámetro (en estadística): Cierta cantidad que caracteriza de alguna forma a la población, como su media o su mediana
- ↑ Serret Moreno-Gil, Jaime. Procedimientos estadísticos. [S.l.: s.n.] p. 71. ISBN 8473561716.
En estadística descriptiva tenemos una serie de expresiones (...) que permiten disponer de unos valores numéricos que reflejan el comportamiento global del suceso estadístico, calculados a partir de los datos individuales. Estas expresiones son los parámetros estadísticos
- ↑ citado por Calot (1985, pp. 55, 56) y MAD-Eduforma (2006, p. 160)
- ↑ Métodos estadísticos en Ingeniería. [S.l.: s.n.] pp. 39–41. ISBN 8497057279
- ↑ «Medidas de Dispersión». Enciclopedia Microsoft® Encarta® Online. Microsoft Corporation. 2009. Consultado em 28 de novembro de 2015
|arquivourl=é mal formado: timestamp (ajuda) - ↑ Serret Moreno-Gil, Jaime. Procedimientos estadísticos. [S.l.: s.n.] 81 páginas. ISBN 8473561716
- ↑ Wackerly, Dennis D; Mendenhall, William; Scheaffer, Richard L. Estadística matemática con aplicaciones. [S.l.: s.n.] p. 8. ISBN 9706861947.
La medida central que más se usa en estadística es la media aritmética
- ↑ Bioestadística. Métodos y aplicaciones. [S.l.: s.n.] ISBN 84-7496-653-1. Consultado em 23 de dezembro de 2009. Arquivado do original em 23 de dezembro de 2009
- ↑ Wackerly, Dennis D; Mendenhall, William; Scheaffer, Richard L. Estadística matemática con aplicaciones. [S.l.: s.n.] p. 8. ISBN 9706861947.
Dos conjuntos de mediciones podrían tener distribuciones de frecuencias muy distintas, pero con la misma media
- ↑ Rius Díaz, Francisca. «2.3.6 La moda». Bioestadística. Métodos y aplicaciones. [S.l.: s.n.]
- ↑ Santos, María José (abril de 2009). «Retrato robot del alcalde metropolitano». El Correo de Andalucía. Consultado em 7 de abril de 2009
- ↑ Serret Moreno-Gil, Jaime. Procedimientos estadísticos. [S.l.: s.n.] 75 páginas. ISBN 8473561716
- ↑ Rius Díaz, Francisca. «2.3.4 La mediana». Bioestadística. Métodos y aplicaciones. [S.l.: s.n.]
- ↑ Martín Andrés, Antonio; Luna del Castillo; Juan de Dios (2004). Bioestadística para las ciencias de la Salud. [S.l.]: Capitel Editores. p. 28. ISBN 8484510182. Consultado em 17 de abril de 2009
- ↑ a b Huff, Darrel (1965). «2. El promedio bien escogido». Cómo mentir con estadísticas. Acapulco: Sagitario
- ↑ Johnson, Robert; Kuby, Patricia (2003). «2.8. El arte del engaño estadístico». Estadística elemental 3ª ed. [S.l.]: Cengage Learning Editores. 94 páginas. ISBN 9706862870
- ↑ a b Rius Díaz, Francisca. «2.7. Medidas de variabilidad o dispersión». Bioestadística. Métodos y aplicaciones. [S.l.: s.n.] Consultado em 17 de abril de 2009
- ↑ Férnandez Fernández, Santiago; Alejandro Córdoba; José María Cordero Sánchez; Alejandro Córdoba (2002). «4.2. Medidas absolutas». Estadística Descriptiva 2ª ed. [S.l.]: ESIC Editorial. p. 192. ISBN 8473563069
- ↑ a b Rius Díaz, Francisca. «2.7.4. Varianza y desviación típica». Bioestadística. Métodos y aplicaciones. [S.l.: s.n.] Consultado em 7 de abril de 2009
- ↑ Wackerly, Dennis D. «3.11. Teorema de Chebyshev». Estadística matemática con aplicaciones. [S.l.: s.n.] p. 139
- ↑ Férnandez Fernández, Santiago. «4.2.3.4. Meda o desviación mediana». Estadística Descriptiva. [S.l.: s.n.] p. 200
- ↑ Férnandez Fernández, Santiago. «4.3. Medidas relativas». Estadística Descriptiva. [S.l.: s.n.] p. 201
- ↑ Férnandez Fernández, Santiago. «4.3. Medidas relativas». Estadística Descriptiva. [S.l.: s.n.] p. 202
- ↑ Sotomayor Velasco, Gabriel; Wisniewski, Piotr Marian (2001). «8.7. Momentos y otras características». Probabilidad y estadística para ingeniería y ciencias. [S.l.]: Cengage Learning Editores. p. 196. ISBN 970686136X. Consultado em 7 de abril de 2009
- ↑ Malléa, Adriana, Adriana; Herrera, Myriam; Ruiz, Ana María (2003). «3. Parámetros estadísticos no convencionales». Estadística en el nivel polimodal. San Juan: effha. p. 67. ISBN 9872084920. Consultado em 17 de abril de 2009
- ↑ Llorente Galera, Francisco; Staff, VV; Marín Feria, Susana; Torra Porras, Salvador. Principios de estadística descriptiva aplicada a la empresa. [S.l.: s.n.] pp. 53–54. ISBN 8480044276
- ↑ Wackerly, Dennis D. «3.9. Momentos y funciones generadoras de momentos». Estadística matemática con aplicaciones. [S.l.: s.n.] p. 131
- ↑ «Estadísticos de tendencia central». Cópia arquivada em 23 de dezembro de 2009
- ↑ =Casas Sánchez, J.M; Santos Peña, Julián (2002). «2.6. Momentos». Introducción a la estadística para economía 2 ed. [S.l.]: Ramón Areces. p. 95. ISBN 848004523X.
Si los momentos coinciden en dos distribuciones, diremos que son iguales
- ↑ Cáceres Hernández, Juan José (2007). «4.1. Variable estadística multidimensional y distribución de frecuencias». Conceptos básicos de Estadística para Ciencias Sociales. [S.l.]: Delta Publicaciones. p. 62. ISBN 8496477436
- ↑ Arias Rodríguez; Jose Carlos (2004). «Distribuciones bidimensionales». Proyecto Descartes. Madrid: Ministerio de Educación, Política Social y Deporte. Consultado em 7 de abril de 2009
- ↑ Rius Díaz, Francisca (outubro de 1997). «3.10.2. Una interpretación geométrica de la covarianza». Bioestadística. Métodos y aplicaciones. Málaga: Universidade de Málaga. ISBN 84-7496-653-1. Consultado em 7 de abril de 2009. Cópia arquivada em 23 de dezembro de 2009
- ↑ Barón López; Francisco Javier. «Bioestadística» (Vídeo em Flash). Málaga: Universidade de Málaga. Consultado em 18 de abril de 2009
- ↑ Casas Sánchez, Jose M.; Manzano Arrondo, Vicente; Zamora Sanz, Ana Isabel (1997). «2. Estimación puntual». Inferencia Estadística 2ª, ilustrada ed. [S.l.]: Ramón Areces. pp. 89–162. ISBN 848004263X
- ↑ Álvarez Leiva, Juan Antonio. «Medidas de dispersión». Proyecto CICA Thales. Sociedad Andaluza de Educación Matemática "Thales". Consultado em 7 de abril de 2009
- ↑ Los Simpsons, temporada 5, episodio Homer, o vigilante
Bibliografia[editar | editar código-fonte]
- Calot, Gérard (1985). Curso de estadística descriptiva. trad. Francisco José Cano Sevilla 4ª ed. [S.l.]: Parainfo. ISBN 8428305633
- Férnandez Fernández, Santiago; Córdoba, Alejandro; Cordero Sánchez, José María (2002). Estadística Descriptiva 2ª ed. [S.l.]: ESIC Editorial. ISBN 8473563069
- Huff, Darrel; Geis, Irvin (1993). How to lie with Statistics. [S.l.]: W W Norton & Co Inc. ISBN 0393310728
- Rius Díaz, Francisca (1997). Bioestadística. Métodos y aplicaciones 2ª ed. [S.l.]: Universidad de Málaga. ISBN 84-7496-653-1
- Velasco Sotomayor, Gabriel; Wisniewski, Piotr Marian (2001). Probabilidad y estadística para ingeniería y ciencias. [S.l.]: Cengage Learning Editores. pp. 185–197. ISBN 970686136X
- Técnicos de Administración Del Ministerio de Economía Y Hacienda (instituto Nacional de Estadística). Grupos III Y IV. Temario Específico Y Test Ebook. [S.l.]: MAD-Eduforma. 2006. ISBN 9788466552509