Parâmetros de Denavit-Hartenberg

Os parâmetros de Denavit–Hartenberg (também chamados de parâmetros DH) são quatro parâmetros associados a uma convenção para fixar sistemas de referência aos elos de uma cadeia cinemática espacial, ou manipulador robótico.

Jacques Denavit e Richard Hartenberg introduziram esta convenção em 1955 com o intuito de padronizar as coordenadas de sistemas de referências para ligações espaciais.

Richard Paul demonstrou o seu valor para a análise cinemática de sistemas robóticos em 1981. Embora muitas outras convenções para a fixação de sistemas de referência também tenham sido desenvolvidas, a convenção de Denavit-Hartenberg continua a ser uma abordagem popular.

Convenção de Denavit-Hartenberg

Nesta convenção, sistemas de coordenadas são fixados a articulações entre dois elos, de forma que uma transformação seja associada à articulação $[Z]$, e a segunda transformação seja associada ao elo $[X]$. As transformações de coordenadas ao longo de um robô em série consistindo de n elos resulta nas equações cinemáticas do robô,

$[T]=[Z_{1}][X_{1}][Z_{2}][X_{2}]\ldots [X_{n-1}][Z_{n}],\!$

onde $[T]$ é a transformação localizando o elo final.

A fim de determinar as transformações de coordenadas $[Z]$ e $[X]$, as articulações conectando os elos são modeladas como juntas rotacionais ou prismáticas, cada uma das quais tendo uma linha única $S$ no espaço que constitui o eixo da articulação e define o movimento relativo dos dois elos. Um robô em série típico é caracterizado por uma sequência de seis linhas $S_{i}$, i=1,...,6, uma para cada junta do robô. Para cada sequência de linhas $S_{i}$ e $S_{i+1}$, existe uma linha normal de $A_{i,i+1}$. O sistema de seis eixos de juntas $S_{i}$ e cinco linhas normais comuns $A_{i,i+1}$ formam o esqueleto cinemático do robô em série típico de seis graus de liberdade. Denavit e Hartenberg introduziram a convenção de que eixos de coordenadas $Z$ são fixados aos eixos de juntas $S_{i}$ e eixos de coordenadas $X$ são fixados às normais comuns $A_{i,i+1}$.

Essa convenção permite a definição do movimento de elos em torno de um eixo da articulação comum $S_{i}$ por deslocamento de parafuso,

$[Z_{i}]={\begin{bmatrix}\cos \theta _{i}&-\sin \theta _{i}&0&0\\\sin \theta _{i}&\cos \theta _{i}&0&0\\0&0&1&d_{i}\\0&0&0&1\end{bmatrix}},$

onde θ_i é a rotação e d_i é o deslizamento ao longo do eixo $Z$. Um dos parâmetros pode ser constante, dependendo da estrutura do robô. Com essa convenção, as dimensões de cada elo na ligação em série são definidas pelo deslocamento de parafuso em torno da normal comum $A_{i,i+1}$ a partir da junta $S_{i}$ até $S_{i+1}$, que é dado por

$[X_{i}]={\begin{bmatrix}1&0&0&r_{i,i+1}\\0&\cos \alpha _{i,i+1}&-\sin \alpha _{i,i+1}&0\\0&\sin \alpha _{i,i+1}&\cos \alpha _{i,i+1}&0\\0&0&0&1\end{bmatrix}},$

onde α_i,i+1 e i_i,i+1 definem as dimensões físicas do elo em termos do ângulo e da distância ao longo do eixo $X$.

Em resumo, os sistemas de referência são estabelecidos como se segue:

1. o eixo $z$ fica na direção do eixo da junta
   
2. o eixo $x$ é paralelo à normal comum: $x_{n}=z_{n}\times z_{n-1}$
   Se não há uma normal comum única (eixos $z$ paralelos) então $d$ (abaixo) é um parâmetro livre. A direção de $x_{n}$ vai de $z_{n-1}$ para $z_{n}$.
3. o eixo $y$ é escolhido depois de $x$ e $z$ de maneira que forme um sistema de coordenadas cartesiano.

Quatro parâmetros

Os quatros parâmetros da convenção clássica de DH estão demonstrados em texto vermelho, sendo eles $\theta _{i},d_{i},a_{i},\alpha _{i}$. Com esses 4 parâmetros, podemos transladar as coordenadas de $O_{i-1}X_{i-1}Y_{i-1}Z_{i-1}$ para $O_{i}X_{i}Y_{i}Z_{i}$.

Os quatro parâmetros de transformação seguintes são conhecidos como parâmetros DH:

• $d\,$: distância ao longo do $z$ anterior até a normal comum.
• $\theta \,$: ângulo em torno do $z$ anterior, do $x$ anterior até o $x$
• $r\,$: comprimento da normal comum (ou seja, $a$, mas usando essa notação cuidado para não confundir com $\alpha$). No caso de uma junta rotacional, este é o raio ao redor do $z$ anterior.
• $\alpha \,$: ângulo em torno da normal comum, do $z$ anterior ao $z$ novo.

Há certa flexibilidade de escolha dos sistemas de coordenadas, já que o eixo $x$ anterior ou o próximo $x$ podem apontar na direção da normal comum. O segundo sistema permite ramificar a cadeia de forma mais eficiente, porque vários sistemas podem apontar para longe de seu ancestral comum, enquanto no layout alternativo, o ancestral só pode apontar para um sucessor. Assim, a notação comumente usada coloca cada eixo $x$ mais próximo do final da cadeia colinear com a normal comum, produzindo os cálculos de transformação mostrados abaixo.

Podemos observar as seguintes restrições nas relações entre os eixos:

• o eixo $x_{n}$ é perpendicular à ambos os eixos $z_{n-1}$ e $z_{n}$
• o eixo $x_{n}$  cruza tanto o eixo $z_{n-1}$ quanto o eixo $z_{n}$
• a origem da junta $n$ fica na interseção de $x_{n}$ com $z_{n}$
• $y_{n}$ completa as coordenadas da mão direita baseado em $x_{n}$ e $z_{n}$

Matriz de Denavit-Hartenberg

É comum separar um deslocamento de parafuso no produto entre transação pura ao longo de uma linha e rotação pura em torno da linha, de modo que

$[Z_{i}]=\operatorname {Trans} _{Z_{i}}(d_{i})\operatorname {Rot} _{Z_{i}}(\theta _{i}),$

e

$[X_{i}]=\operatorname {Trans} _{X_{i}}(r_{i,i+1})\operatorname {Rot} _{X_{i}}(\alpha _{i,i+1}).$

Usando esta notação, cada elo pode ser descrito por uma transformação de coordenadas das coordenadas presente para o sistema de coordenadas anterior.

${}^{n-1}T_{n}=\operatorname {Trans} _{z_{n-1}}(d_{n})\cdot \operatorname {Rot} _{z_{n-1}}(\theta _{n})\cdot \operatorname {Trans} _{x_{n}}(r_{n})\cdot \operatorname {Rot} _{x_{n}}(\alpha _{n})$

Note que este é o produto de dois deslocamentos de parafuso. As matrizes associadas a estas operações são:

$\operatorname {Trans} _{z_{n-1}}(d_{n})=\left[{\begin{array}{ccc|c}1&0&0&0\\0&1&0&0\\0&0&1&d_{n}\\\hline 0&0&0&1\end{array}}\right]$

$\operatorname {Rot} _{z_{n-1}}(\theta _{n})=\left[{\begin{array}{ccc|c}\cos \theta _{n}&-\sin \theta _{n}&0&0\\\sin \theta _{n}&\cos \theta _{n}&0&0\\0&0&1&0\\\hline 0&0&0&1\end{array}}\right]$

$\operatorname {Trans} _{x_{n}}(r_{n})=\left[{\begin{array}{ccc|c}1&0&0&r_{n}\\0&1&0&0\\0&0&1&0\\\hline 0&0&0&1\end{array}}\right]$

$\operatorname {Rot} _{x_{n}}(\alpha _{n})=\left[{\begin{array}{ccc|c}1&0&0&0\\0&\cos \alpha _{n}&-\sin \alpha _{n}&0\\0&\sin \alpha _{n}&\cos \alpha _{n}&0\\\hline 0&0&0&1\end{array}}\right]$

Que resulta em:

$\operatorname {} ^{n-1}T_{n}=\left[{\begin{array}{ccc|c}\cos \theta _{n}&-\sin \theta _{n}\cos \alpha _{n}&\sin \theta _{n}\sin \alpha _{n}&r_{n}\cos \theta _{n}\\\sin \theta _{n}&\cos \theta _{n}\cos \alpha _{n}&-\cos \theta _{n}\sin \alpha _{n}&r_{n}\sin \theta _{n}\\0&\sin \alpha _{n}&\cos \alpha _{n}&d_{n}\\\hline 0&0&0&1\end{array}}\right]=\left[{\begin{array}{ccc|c}&&&\\&R&&T\\&&&\\\hline 0&0&0&1\end{array}}\right]$

onde R é a sub-matriz 3×3 que descreve a rotação e T é a sub-matriz 3×1 que descreve a translação.

Uso das matrizes de Denavit e Hartenberg

A notação de Denavit e Hartenberg provê uma metodologia padrão para escrever as equações cinemáticas de um manipulador. Isto é especialmente útil para a manipuladores em série, onde uma matriz é usada para representar a pose (posição e orientação) de um corpo em relação a outro.

A posição do corpo $n$ em relação ao $n-1$ pode ser representada por uma matriz de posição indicada com o símbolo $T$ ou $M$

$\operatorname {} ^{n-1}T_{n}=M_{n-1,n}$

Esta matriz também é usada para transformar um ponto do sistema $n$ para $n-1$

$M_{n-1,n}=\left[{\begin{array}{ccc|c}R_{xx}&R_{xy}&R_{xz}&T_{x}\\R_{yx}&R_{yy}&R_{yz}&T_{y}\\R_{zx}&R_{zy}&R_{zz}&T_{z}\\\hline 0&0&0&1\end{array}}\right]$

Onde a sub-matriz $3\times 3$ do canto superior esquerdo de $M$ representa orientação relativa de dois corpos, e a $3\times 1$ do canto superior direito representa a sua posição relativa ou, mais especificamente, a posição do corpo no sistema $n-1$ representado com o elemento do sistema $n$.

A posição do corpo $k$ em relação ao corpo $i$ pode ser obtida como o produto de matrizes que representam a pose de $j$ em relação a $i$ e a de $k$ em relação a $j$

$M_{i,k}=M_{i,j}M_{j,k}$

Uma propriedade importante das matrizes de Denavit e Hartenberg é que o inverso é

$M^{-1}=\left[{\begin{array}{ccc|c}&&&\\&R^{T}&&-R^{T}T\\&&&\\\hline 0&0&0&1\end{array}}\right]$

onde $R^{T}$ é tanto a transposição quanto a inversçao da matriz ortogonal $R$, ou seja $R_{ij}^{-1}=R_{ij}^{T}=R_{ji}$.

Cinemática

Mais matrizes podem ser definidas para representar a velocidade e a aceleração dos corpos. A velocidade do corpo $i$ em relação ao corpo $j$ pode ser representada no sistema $k$ pela matriz

$W_{i,j(k)}=\left[{\begin{array}{ccc|c}0&-\omega _{z}&\omega _{y}&v_{x}\\\omega _{z}&0&-\omega _{x}&v_{y}\\-\omega _{y}&\omega _{x}&0&v_{z}\\\hline 0&0&0&0\end{array}}\right]$

onde $\omega$ é a velocidade angular do corpo $j$ em relação ao corpo $i$ e todos os componentes estão expressos no sistema $k$; $v$ é a velocidade linear de um ponto do corpo $j$ em relação ao corpo $i$ (o polo). O polo é o ponto de $j$ que passa pela origem do sistema $i$.

A matriz de aceleração pode ser definida como a soma da derivada no tempo da velocidade mais a velocidade ao quadrado

$H_{i,j(k)}={\dot {W}}_{i,j(k)}+W_{i,j(k)}^{2}$

A velocidade e a aceleração no sistema $i$ de um ponto do corpo $j$ podem ser avaliadas como

${\dot {P}}=W_{i,j}P$

${\ddot {P}}=H_{i,j}P$

Também é possível provar que

${\dot {M}}_{i,j}=W_{i,j(i)}M_{i,j}$

${\ddot {M}}_{i,j}=H_{i,j(i)}M_{i,j}$

As matrizes de velocidade e aceleração se adicionam de acordo com as seguintes regras:

$W_{i,k}=W_{i,j}+W_{j,k}$

$H_{i,k}=H_{i,j}+H_{j,k}+2W_{i,j}W_{j,k}$

em outras palavras, a velocidade absoluta é a soma do arrasto mais a velocidade relativa; pois o termo da aceleração de Coriolis também está presente.

Os componentes das matrizes de velocidade e aceleração são expressos em um sistema $k$ arbitrário e transformam de um sistema para o outro pela seguinte regra

$W_{(h)}=M_{h,k}W_{(k)}M_{k,h}$

$H_{(h)}=M_{h,k}H_{(k)}M_{k,h}$

Dinâmica

Para a dinâmica, 3 outras matrizes são necessárias para descrever o momento de inércia $J$, o momento linear e angular $\Gamma$ e as forças e torques $\Phi$ aplicadas a um corpo.

Inércia $J$:

$J=\left[{\begin{array}{ccc|c}I_{xx}&I_{xy}&I_{xz}&x_{g}m\\I_{yx}&I_{yy}&I_{yz}&y_{g}m\\I_{xz}&I_{yz}&I_{zz}&z_{g}m\\\hline x_{g}m&y_{g}m&z_{g}m&m\end{array}}\right]$

onde $m$ é a massa, $x_{g},\,y_{g},\,z_{g}$ representam a posição do centro de massa, e os termos $I_{xx},\,I_{xy},\ldots$ representam a inércia e são definidos como

$I_{xx}=\int \int x^{2}\,dm$

$I_{xy}=\int \int xy\,dm$

$I_{xz}=\cdots$

$\cdots$

Matriz de ação $\Phi$, contendo força $f$ e torque $t$:

$\Phi =\left[{\begin{array}{ccc|c}0&-t_{z}&t_{y}&f_{x}\\t_{z}&0&-t_{x}&f_{y}\\-t_{y}&t_{x}&0&f_{z}\\\hline -f_{x}&-f_{y}&-f_{z}&0\end{array}}\right]$

Matriz de quantidade de movimento $\Gamma$ contendo impulsos linear $\rho$ e angular $\gamma$

$\Gamma =\left[{\begin{array}{ccc|c}0&-\gamma _{z}&\gamma _{y}&\rho _{x}\\\gamma _{z}&0&-\gamma _{x}&\rho _{y}\\-\gamma _{y}&\gamma _{x}&0&\rho _{z}\\\hline -\rho _{x}&-\rho _{y}&-\rho _{z}&0\end{array}}\right]$

Todas as matrizes são representadas com os componentes do vetor em um determinado sistema $k$. A transformação dos componentes do sistema $k$ para o sistema $h$ segue a regra

$J_{(h)}=M_{h,k}J_{(k)}M_{h,k}^{T}$

$\Gamma _{(h)}=M_{h,k}\Gamma _{(k)}M_{h,k}^{T}$

$\Phi _{(h)}=M_{h,k}\Phi _{(k)}M_{h,k}^{T}$

As matrizes descritas permitem escrever as equações de dinâmica de uma forma concisa.

A lei de Newton:

$\Phi =HJ-JH^{t}\,$

Quantidade de movimento:

$\Gamma =WJ-JW^{t}\,$

A primeira destas equações expressa a lei de Newton e é equivalente do à equação de vetor $f=ma$ (força igual a massa vezes aceleração), além de $t=J{\dot {\omega }}+\omega \times J\omega$ (aceleração angular em função do momento de inércia e velocidade angular); a segunda equação permite a avaliação do momento linear e angular quando a velocidade e a inércia são conhecidas.

Parâmetros DH modificados

Alguns livros como o "Introduction to Robotics: Mechanics and Control (3rd Edition) usam parâmetros DH modificados. A diferença entre os parâmetros DH clássicos e os modificados são os locais dos sistemas de coordenadas e a ordem das transformações.

Parâmetros DH modificados

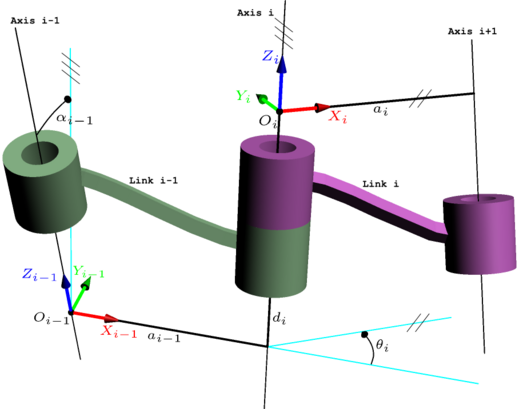
Em comparação com os parâmetros DH clássicos, as coordenadas do sistema $O_{i-1}$ são colocadas no eixo i-1, não no eixo i como na convenção clássica. As coordenadas de $O_{i}$ são colocadas sobre o eixo i, e não o eixo i+1 como na convenção clássica.

Outra diferença é que, de acordo com a modificação da convenção, a matriz de transformação é dada pela seguinte ordem de operações:

${}^{n-1}T_{n}=\operatorname {Rot} _{x_{n-1}}(\alpha _{n-1})\cdot \operatorname {Trans} _{x_{n-1}}(a_{n-1})\cdot \operatorname {Rot} _{z_{n}}(\theta _{n})\cdot \operatorname {Trans} _{z_{n}}(d_{n})$

Assim, a matriz de parâmetros DH modificados torna-se

$\operatorname {} ^{n-1}T_{n}=\left[{\begin{array}{ccc|c}\cos \theta _{n}&-\sin \theta _{n}&0&a_{n-1}\\\sin \theta _{n}\cos \alpha _{n-1}&\cos \theta _{n}\cos \alpha _{n-1}&-\sin \alpha _{n-1}&-d_{n}\sin \alpha _{n-1}\\\sin \theta _{n}\sin \alpha _{n-1}&\cos \theta _{n}\sin \alpha _{n-1}&\cos \alpha _{n-1}&d_{n}\cos \alpha _{n-1}\\\hline 0&0&0&1\end{array}}\right]$

Deve ser digna de nota a observação de que alguns livros (por exemplo:) usam $a_{n}$ e $\alpha _{n}$ para indicar o comprimento e a torção do elo n-1 em vez do elo n. Como consequência, ${}^{n-1}T_{n}$ é formado apenas com parâmetros usando o mesmo índice.

Pesquisas sobre as convenções de DH e suas diferenças foram publicadas.

Veja também

• Cinemática inversa
• Cinemática