Paradoxo de Klein

Em 1929, o físico Oskar Klein obteve um resultado surpreendente através da aplicação da equação de Dirac para o problema familiar de espalhamento de elétrons por uma barreira de potecial. Na mecânica quântica não-relativística, o tunelamento de elétrons em uma barreira é observado, com amortecimento exponencial. No entanto, o resultado de Klein mostrou que, se o potencial é da ordem da massa do elétron, $V\sim mc^{2}$, a barreira é quase transparente. Além disso, conforme o potencial se aproxima do infinito, a reflexão diminui e o elétron é sempre transmitido.

A aplicação imediata do paradoxo foi o modelo próton-elétron de Rutherford para partículas neutras dentro do núcleo, antes da descoberta do nêutron. O paradoxo apresentou uma objeção quântica com a noção de um elétron confinado dentro de um núcleo. Este paradoxo claro e preciso sugeriu que um elétron não pode ser confinado dentro de um núcleo por qualquer poço de potencial. O significado desse paradoxo foi intensamente debatida na ocasião.

Partículas sem massa

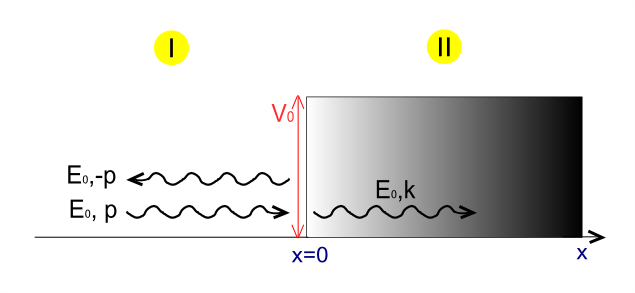
Considere uma partícula sem massa relativistica se aproximando de um potencial degrau de altura $V_{0}$ com energia $E_{0}<V_{0}$ e momento $p$.

A função de onda da partícula, $\psi$, segue a equação de Dirac independente do tempo:

$\left(\sigma _{x}p+V\right)\psi =E_{0}\psi ,\quad V={\begin{cases}0,&x<0\\V_{0},&x>0\end{cases}}$

E $\sigma _{x}$ é a matriz de Pauli:

$\sigma _{x}=\left({\begin{matrix}0&1\\1&0\end{matrix}}\right)$

Fig. 1 Descrição da relação de dispersão, o eixo x representa o momento enquanto que o eixo y representa a energia.

Assumindo que a partícula está se propagando a partir da esquerda, obtemos duas soluções — um antes do degrau, na região (1) e um abaixo do potencial, na região (2):

$\psi _{1}=Ae^{ipx}\left({\begin{matrix}1\\1\end{matrix}}\right)+A'e^{-ipx}\left({\begin{matrix}-1\\1\end{matrix}}\right),\quad p=E_{0}\,$

$\psi _{2}=Be^{ikx}\left({\begin{matrix}1\\1\end{matrix}}\right),\quad \left|k\right|=V_{0}-E_{0}\,$

Onde os coeficientes A, A′ e B são números complexos. Ambas as funções de onda incidente e transmitida estão associados com velocidade de grupo positiva (Linhas azuis na Fig.1), enquanto que a função de onda refletida é associado com velocidade de grupo negativa. (Linhas verdes na Fig.1)

Agora queremos calcular os coeficientes de transmissão e reflexão, $T,R.$ Eles são derivados da correntes de amplitude de probabilidade.

A definição da corrente de probabilidade associada com a equação de Dirac é:

$J_{i}=\psi _{i}^{\dagger }\sigma _{x}\psi _{i},\ i=1,2\,$

Nesse caso:

$J_{1}=2\left[\left|A\right|^{2}-\left|A'\right|^{2}\right],\quad J_{2}=2\left|B\right|^{2}\,$

Os coeficientes de transmissão e reflexão são:

$R={\frac {\left|A'\right|^{2}}{\left|A\right|^{2}}},\quad T={\frac {\left|B\right|^{2}}{\left|A\right|^{2}}}\,$

A continuidade da função de onda em $x=0$, nos fornece:

$\left|A\right|^{2}=\left|B\right|^{2}\,$

$\left|A'\right|^{2}=0\,$

E assim, o coeficiente de transmissão é 1 e não há reflexão.

Uma interpretação do paradoxo é de que um potencial degrau não pode inverter a direção da velocidade de grupo de uma partícula relativística sem massa. Esta explicação se adéqua melhor a solução de partícula única citada acima. Interpretações mais complexas são sugeridas na literatura, no contexto da teoria quântica de campos onde é mostrado que o tunelamento desenfreado ocorre devido à existência de pares de partículas-antipartícula no potencial.

Caso massivo

Para o caso massivo, os cálculos são semelhantes ao descrito acima. Os resultados são tão surpreendente como no caso sem massa. O coeficiente de transmissão é sempre maior do que zero, e se aproxima de 1 conforme o potencial degrau tende a infinito.

A zona Klein

Se a energia da partícula está na faixa $+m<E<V-m$, então resultará em uma reflexo parcial ao invés de reflexão total.

Resoluções para o caso massivo

Enquanto a resolução tradicional utiliza produção de pares partícula / antipartícula no contexto da teoria quântica de campos (Hansen 1981), existe uma resolução mais simples que substitui a produção de pares físicos por um espalhamento de soluções de energia negativa sob a barreira (Alhaidari 2009). Esta estratégia foi também aplicada para obter soluções analíticas para a equação de Dirac para um poço quadrado infinito.

Outros casos

Estes resultados foram expandidos para dimensões maiores, e para outros tipos de potenciais, tais como um degrau linear, uma barreira quadrada, etc. Muitas experiências em transporte de elétrons no grafeno apoiam-se no paradoxo Klein para partículas sem massa.

Leituras adicionais

• Dombey, N; Calogeracos, A. (julho de 1999). «Seventy years of the Klein paradox». Physics Reports. 315 (1–3): 41–58. Bibcode:1999PhR...315...41D. doi:10.1016/S0370-1573(99)00023-X 
• Robinson, T. R. (2012). «On Klein tunneling in graphene». American Journal of Physics. 80 (2): 141–147. Bibcode:2012AmJPh..80..141R. doi:10.1119/1.3658629 
• Calogeracos, A.; Dombey, N. (1999). «History and physics of the Klein paradox». Contemporary Physics. 40 (5). 313 páginas. Bibcode:1999ConPh..40..313C. arXiv:quant-ph/9905076. doi:10.1080/001075199181387 

Ver também

• Lista de paradoxos
• Teoria quântica de campos
• Equação de Dirac