Usuária:MCarrera (NeuroMat)/Testes/Mediana (fórmulas)

0 – Mediana

Teoria das probabilidades
Axiomas de probabilidade
Espaço de probabilidade Espaço amostral Evento primário Evento Variável aleatória Medida de probabilidade
Evento complementar Eventos mutuamente exclusivos Probabilidade conjunta Probabilidade marginal Probabilidade condicional
Independência Independência condicional Lei da probabilidade total Lei dos grandes números Teorema de Bayes Desigualdade de Boole
Diagrama de Venn Diagrama de árvore

1 – Mediana é o valor que separa a metade maior e a metade menor de uma amostra, uma população ou uma distribuição de probabilidade. Em termos mais simples, mediana pode ser o valor do meio de um conjunto de dados. No conjunto de dados {1, 3, 3, 6, 7, 8, 9} abre chaves 1, 3, 3, 6, 7, 8, 9 fecha chaves a mediana é 6. Se houver um número par de observações, não há um único valor do meio. Então, a mediana é definida como a média dos dois valores do meio. No conjunto de dados {3, 5, 7, 9} abre chaves 3, 5, 7, 9 fecha chaves, a mediana é ${\frac {5+7}{2}}=6$ 5 mais 7 sobre 2 igual a 6.

2 – A mediana é uma medida comum das propriedades de conjuntos de dados em estatística e em teoria das probabilidades, com importância central na estatística robusta. A estatística robusta é mais resistente, com ponto de ruptura de 50%. A mediana não fornece resultados arbitrariamente grande desde que mais da metade dos dados não esteja contaminada.

3 – A vantagem da mediana em relação à média é que a mediana pode dar uma ideia melhor de um valor típico porque não é tão distorcida por valores extremamente altos ou baixos. Em estudos estatísticos sobre renda familiar ou outros ativos voláteis, a média pode ser distorcida por um pequeno número de valores extremamente altos ou baixos.

4 – História

Pierre Simon Laplace

5 – A ideia de mediana aparece no século XIII no Talmude e mais tarde no livro Certaine Errors in Navigation, na seção sobre determinação da localização com bússola. O livro foi escrito pelo matemático Edward Wright em 1599, que achou que o valor era o mais provável de ser o correto em uma série de observações.

6 – Em 1757, Ruđer Bošković desenvolve um método de regressão baseado no espaço Lp e implicitamente na mediana. Em 1774, Pierre Simon Laplace sugere o uso da mediana como o estimador padrão do valor de um pdf posterior. O critério foi minimizar a magnitude esperada do erro $|\alpha -\alpha ^{*}|$módulo de alpha–minúsculo menos alpha–minúsculo elevado a asterisco, em que $\alpha ^{*}$ alpha–minúsculo elevado a asterisco é a estimativa e $\alpha$ alpha–minúsculo é o valor real. O método de Laplace foi amplamente rejeitado por 150 anos em favor do método dos mínimos quadrados de Carl Friedrich Gauss e de Adrien-Marie Legendre, o qual minimiza $(\alpha -\alpha ^{*})^{2}$ abre parênteses alpha–minúsculo menos alpha–minúsculo elevado a asterisco fecha parênteses elevado a dois para obter a média. A distribuição tanto da média da amostra quanto da mediana da amostra foi determinada por Laplace no início dos anos 1800.

7 – Em 1843, Antoine Augustin Cournot foi o primeiro matemático a usar o termo mediana para o valor que divide a distribuição de probabilidade em duas metades iguais. Gustav Fechner usou o termo mediana para fenômenos sociológicos e psicológicos. Mediana tinha sido usada anteriormente apenas na astronomia e em áreas correlatas. Embora tenha sido usada anteriormente por Laplace, Fechner popularizou a mediana na análise formal de dados.

8 – Em 1881, Francis Galton usou o termo mediana em Inglês depois de usar os termos middle-most value em 1869 e medium em 1880.

9 – Imagem. Pierre Simon Laplace.

10 – Conceitos básicos

Comparação entre média (mean, em inglês), mediana (median, em inglês) e moda (mode, em inglês) de duas distribuições log–normal com diferentes distorções.

11 – A mediana é usada principalmente em distribuições distorcidas, que resumem diferentemente da média aritmética. Seja o multiconjunto {1, 2, 2, 2, 3, 14} abre chaves, um, vírgula dois, vírgula dois, vírgula dois, vírgula três, vírgula quatorze. Fecha chaves. . Por ser menos susceptível a valores excepcionalmente altos ou baixos, a mediana de valor 2 pode ser uma melhor indicação de tendência central que a média aritmética de valor 4.

12 – Mediana é uma técnica comum na summary statistics e summarizing statistical data, uma vez que é fácil de calcular e simples de entender e fornece uma medida mais robusta na presença de outliers (valores atípicos) que a média. Entretanto, a relação empírica amplamente citada entre as localizações relativas da média e da mediana para distribuições distorcidas geralmente não é verdadeira. No entanto, há várias relações para a diferença absoluta entre elas.

13 – Mediana não identifica um valor específico dentro de um conjunto de dados, uma vez que mais de um valor pode ter o valor da mediana. Com um número par de observações, nenhum valor precisa ter exatamente o valor da mediana. Porém, o valor da mediana é unicamente determinado pela definição usual. Um conceito relacionado em que o resultado corresponde a um elemento da amostra é o medoide.

14 – Em uma população, no máximo metade da amostra tem valores estritamente menores que a média e no mínimo metade da amostra tem valores estritamente maiores que a mediana. Se cada grupo tem menos da metade da amostra, então parte da amostra é exatamente igual a mediana. Se $a<b<c$ a–minúsculo menor que b–minúsculo menor que c–minúsculo , então a mediana da amostra {a, b, c} abre chaves a–minúsculo b–minúsculo c–minúsculo fecha chaves é igual a b b–minúsculo. Se $a<b<c<d$ a–minúsculo menor que b–minúsculo menor que c–minúsculo menor que d–minúsculo , então a mediana da amostra {a, b​​, c, d} abre chaves a'–'minúsculo b'–'minúsculo c'–'minúsculo d'–'minúsculo fecha chaves é igual a média entre b b–minúsculo e c c–minúsculo ou igual a ${\frac {b+c}{2}}$ b'–'minúsculo mais c'–'minúsculo sobre 2.

15 – Como é baseada no valor do meio de um conjunto de dados, não é necessário saber os valores dos elementos extremos para calcular a mediana. Seja um teste psicológico que pretende investigar o tempo necessário para resolver um problema. Se um pequeno número de pessoas não conseguir resolver um problema em um determinado tempo, a mediana ainda pode ser calculada.

16 – Imagem. Comparação entre média (mean, em inglês), mediana (median, em inglês) e moda (mode, em inglês) de duas distribuições log–normal com diferentes distorções.

17 – Cálculos básicos

Em cima: a mediana (median, em inglês) de um conjunto de dados com número ímpar de elementos. Embaixo: a mediana (median, em inglês) de um conjunto de dados com número par de elementos.

18 – A mediana de uma lista finita de números pode ser encontrada organizando os números do menor para o maior.

19 – Se houver um número ímpar de elementos, o número do meio é o valor do meio ${\frac {n+1}{2}}$ n–minúsculo mais 1 sobre 2 (na amostra de sete elementos {1, 3, 3, 6, 7, 8, 9} abre chaves 1, 3, 3, 6, 7, 8, 9 fecha chaves, a mediana é 6).

20 – Se houver um número par de elementos, não há um único valor do meio. Então, a mediana é definida como a média dos dois valores do meio ${\frac {n}{2}}$ n–minúsculo sobre 2 e ${\frac {n}{2}}+1$ 'n–minúsculo sobre 2' mais 1 (na amostra de oito elementos {1, 2, 3, 4, 5, 6, 8, 9} abre chaves 1, 2, 3, 4, 5, 6, 7, 8, 9 fecha chaves, a mediana é a média ${\frac {4+5}{2}}=4,5$ 4 mais5 sobre 2 igual a 4,5

21 – Em termos mais técnicos, é a interpretação da mediana como mid–range.

22 – A fórmula usada para encontrar um valor do meio em uma amostra de $n$ elementos é ${\frac {n+1}{2}}$ n–minúsculo mais 1 sobre 2, que fornece tanto o valor médio para um número ímpar de elementos quanto o ponto médio entre dois valores do meio. Em uma amostra de quatorze elementos, o resultado da fórmula é 7,5 e a mediana é a média entre o sétimo e o oitavo elemento (também é possível calcular a mediana com o diagrama ramo-e-folha).

23 – Não há uma notação padrão amplamente aceita para a mediana, mas alguns autores representam a mediana de uma variável $X$ xis–maiúsculo como ${\tilde {X}}$ til sobre xis–maiúsculo , como $\mu _{\frac {1}{2}}$mi–minúsculo sub–escrito um sobre dois e às vezes como $M$ m–maiúsculo . Em qualquer um dos casos, o uso dos mesmos ou de outros símbolos para a mediana precisam ser explicitamente definidos quando são introduzidos.

A – Imagem. Em cima: a mediana (median, em inglês) de um conjunto de dados com número ímpar de elementos. Embaixo: a mediana (median, em inglês) de um conjunto de dados com número par de elementos.

24 – Exemplos

Ilustração do cálculo da mediana para uma população com número ímpar de valores. Em uma população com número ímpar de valores, a mediana é o valor que separa a metade maior e a metade menor de uma amostra. Para a população {2, 2, 3, 7, 8, 9, 9}, a mediana é 7.

25 – População com número de elementos ímpar

26 – Para a população $\{1,3,5,7,9\}$ abre chaves 1, 3, 5, 7, 9 fecha chaves , o valor médio é:

${\frac {n+1}{2}}={\frac {5+1}{2}}=3$, n–minúsculo mais 1 sobre 2 igual a 5 mais 1 sobre dois igual a 3.

em que $n$ n–minúsculo é o número de dados ou elementos da amostra.

27 – Logo a mediana é o terceiro elemento (5) e é igual a média (5).

29 – Já para a população $\{1,2,4,10,13\}$ abre chaves 1, 2, 4, 10, 13 fecha chaves, o valor médio é:

${\frac {n+1}{2}}={\frac {5+1}{2}}=3$, 'n–minúsculo mais 1 sobre 2 igual a 5 mais 1 sobre dois igual a 3.'

em que $n$ é o número de dados ou elementos da amostra.

30 – Logo a mediana é o terceiro elemento (4), mas não é igual a média (6).

31 – População com número de elementos par

32 – Para a população $\{1,2,4,8,9,10\}$abre chaves 1, 2, 4, 8, 9, 10 fecha chaves, não há valor com a posição 3,5. Logo a mediana é calculada por meio da média dos valores centrais, o terceiro e o quarto elemento. O valor da mediana é:

${\frac {4+8}{2}}=6$ 4 mais 8 sobre 2 igual a 6. Já o valor da média é 7.

33 – Em um conjunto de dados com números repetitivos $\{4,5,5,6,6,6,6,6,[6,7],7,8,8,9,9,10,11,13\}$abre chaves 4, 5, 5, 6, 6, 6, 6, 6, 6, 7, 7, 8, 8, 9, 9, 10, 11, 13 fecha chaves a mediana também é calculada por meio da média dos valores centrais, o nono e o décimo elemento. O valor da mediana é:

${\frac {6+7}{2}}=6,5$ 6 mais 7 sobre 2 igual a 6,5.

A – Imagem. Ilustração do cálculo da mediana para uma população com número ímpar de valores. Em uma população com número ímpar de valores, a mediana é o valor que separa a metade maior e a metade menor de uma amostra. Para a população {2, 2, 3, 7, 8, 9, 9}, a mediana é 7.

36 – Medida de tendência central

Visualização geométrica da moda (mode, em inglês), mediana (median, em inglês) e média (mean, em inglês) de uma função densidade arbitrária.

37 – Mediana para dados ordenados

38 – Mediana pode ser usada como medida de localização quando a distribuição é distorcida, quando os valores finais não são conhecidos ou quando importâncias reduzidas são anexadas aos outliers (por exemplo, quando podem existir erros de medição). A mediana é definida por dados unidimensionais ordenados e é independente de qualquer distância métrica (por exemplo, a média geométrica é definida pot qualquer número de dimensões).

39 – A mediana é uma das alternativas para resumir os valores típicos associados aos elementos da população estatística. Logo, a mediana é um possível parâmetro de localização. A mediana é o 2° quartil, 5° decil e 50° percentil. Ela pode ser calculada para dados ordenadas, mas não para dados categóricos (por exemplo, é possível calcular a mediana das notas de estudantes avaliados entre A e F, mas não é possível calcular a mediana entre os sexos ou entre as nacionalidades de estudantes).

40 – Quando a mediana é usada como parâmetro de localização na estatística descritiva, há várias opções de medidas de dispersão como a amplitude, o intervalo interquartil, o desvio absoluto da média e o desvio absoluto da mediana.

41 – Para objetivos práticos, diferentes medidas de localização e de dispersão são frequentemente comparados com base em o quão bem os valores populacionais correspondentes podem ser estimados a partir da amostra. Inclusive, a mediana tem boas propriedades para tais estimativas. Embora não sejam geralmente ótimas, as propriedades da mediana são razoavelmente boas quando determinada distribuição de população é conhecida.

42 – Por exemplo, a comparação da eficiência de estimadores candidatos mostra que a média amostral é mais eficiente que a mediana amostral quando os dados não estão contaminados por dados de distribuições de cauda pesada ou de misturas de distribuição, mas que a média amostral é menos eficiente que a mediana amostral em caso contrário, o que acontece em uma ampla variação de distribuições. Especificamente, a mediana tem 64% de eficiência em comparação com a variação mínima da média para amostras normais grandes, o que significa que a variância da mediana é aproximadamente 50% maior de que a variância da média.

A – Imagem. Visualização geométrica da moda (mode, em inglês), mediana (median, em inglês) e média (mean, em inglês) de uma função densidade arbitrária.

43 – Distribuições de probabilidade

Ilustração do comportamento das medidas de tendência central em uma distribuição simétrica (por exemplo, uma distribuição normal) quando alterada a dispersão dos dados. A curva vermelha descreve a densidade de probabilidade no espaço amostral e a linha azul representa a localização da média (azul), da mediana (amarelo) e da moda (verde) do conjunto de dados.

Ilustração do comportamento das medidas de tendência central em uma distribuição assimétrica negativa quando alterada a dispersão dos dados. A curva vermelha descreve a densidade de probabilidade no espaço amostral, a linha azul (à esquerda) representa a média, a linha amarela (ao meio) representa a mediana e a linha verde (à direita) representa a moda do conjunto de dados.

Ilustração do comportamento das medidas de tendência central em uma distribuição assimétrica positiva (por exemplo, uma distribuição qui-quadrado) quando alterada a dispersão dos dados. A curva vermelha descreve a densidade de probabilidade dos dados no espaço amostral, a linha azul (à direita) representa a média, a linha amarela (ao meio) representa a mediana e a linha verde (à esquerda) representa a moda do conjunto de dado

Ilustração do comportamento das medidas de tendência central em uma distribuição bimodal, formada por outras duas distribuições com seus respectivos parâmetros, que transita entre distribuição assimétrica positiva, distribuição assimétrica negativa e distribuição simétrica conforme as dispersões dos dados no espaço amostral são alteradas. A curva vermelha descreve a densidade de probabilidade dos dados no espaço amostral, a linha azul representa a média, a linha amarela representa a mediana e a linha verde representa a moda do conjunto de dados.

44 – Para qualquer distribuição de probabilidade em $\mathbb {R}$ conjunto dos números reais r–maiúsculo com função distribuição acumulada $F$ f–maiúsculo, independentemente do tipo de distribuição de probabilidade contínua, em particular, uma distribuição absoluta contínua com função densidade ou uma distribuição discreta, uma mediana é definida como qualquer número real $m$ m-minúsculo que satisfaz as desigualdades:

$\operatorname {P} (X\leq m)\geq {\frac {1}{2}}{\text{ ou }}\operatorname {P} (X\geq m)\geq {\frac {1}{2}}\,\!$função probabilidade p–maiúsculo de abre parêntesis x–maiúsculo menor ou igual a m–minúsculo fecha parêntesis maior ou igual a 1 sobre 2 ou função de probabilidade p–maiúsculo de abre parêntesis x–maiúsculo maior ou igual a m–minúsculo, fecha parêntesis maior ou igual a 1 sobre 2.

ou igualmente as desigualdades:

$\int _{(-\infty ,m]}dF(x)\geq {\frac {1}{2}}{\text{ ou }}\int _{[m,\infty )}dF(x)\geq {\frac {1}{2}}\,\!$ integral de menos infinito m–minúsculo vezes diferencial d–minúsculo da função f–maiúsculo de x–minúsculo maior ou igual a 1 sobre 2 ou integral de m–minúsculo mais infinito vezes diferencial d–minúsculo da função f–maiúsculo de x–minúsculo maior ou igual a 1 sobre 2.

em que a integral de Lebesgue–Stieltjes é usada.

45 – Para uma distribuição de probabilidade absoluta contínua com função densidade $f$ f–minúsculo, a mediana satisfaz:

$\operatorname {P} (X\leq m)=\operatorname {P} (X\geq m)=\int _{-\infty }^{m}f(x)\,dx={\frac {1}{2}}.\,\!$ função de probabilidade p–maiúsculo de abre parêntesis x–maiúsculo menor ou igual a m–minúsculo fecha parêntesis igual a função de probabilidade p–maiúsculo de abre parêntesis x–maiúsculo maior ou igual a m–minúsculo fecha parêntesis igual a integral de menos infinito até m–minúsculo da função f–minúsculo de x–minúsculo vezes diferencial d–minúsculo x–minúsculo igual a 1 sobre 2.

46 – Qualquer distribuição de probabilidade em $\mathbb {R}$ conjunto dos números reais r–maiúsculo tem pelo menos uma mediana, mas ela pode ter mais de uma mediana. Quando a mediana é única, alguns estatísticos falam da mediana corretamente. Quando a mediana não é única, alguns estatísticos falam da mediana informalmente.

47 – Imagem. Visualização geométrica da moda (mode, em inglês), mediana (median, em inglês) e média (mean, em inglês) de uma função densidade arbitrária.

48 – Medianas de distribuições particulares

49 – Medianas de certos tipos de distribuições podem ser calculadas facilmente a partir dos seus parâmetros. Medianas existem mesmo para algumas distribuições sem média bem definida como a distribuição de Cauchy:

• Uma mediana de uma distribuição simétrica que possui uma média μ mi–minúsculo também possui valor μ mi–minúsculo.
  • Uma mediana de uma distribuição normal com média μ mi–minúsculo e variância σ² sigma–minúsculo elevado ao quadrado possui valor μ mi–minúsculo. Para uma distribuição normal, média = mediana = moda.
  • Uma mediana de uma distribuição uniforme no intervalo [a, b] a–minúsculo b–minúsculo possui valor ${\frac {a+b}{2}}$ a–minúsculo mais b-minúsculo sobre 2, que também é a média.
  • Uma mediana de uma distribuição de Cauchy com parâmetro de localização x₀ início x–minúsculo subscrito 0 e parâmetro de escala y y–minúsculo possui valor x₀ inicio x–minúsculo subscrito 0 (parâmetro de localização).
  • Uma mediana de uma lei de potência x^−a, x–minúsculo elevado a menos a–minúsculo com expoente a > 1 a–minúsculo maior que 1 é 2^{1/(a − 1)}x_min 2 elevado a um sobre a–minúsculo menos 1 vezes x–minúsculo subscrito min em que x_min x–minúsculo subscrito min é o valor mínimo para que a lei de potência exista.
• Uma mediana de uma distribuição exponencial com parâmetro de taxa λ lambda– minúsculo é o logaritmo natural de 2 dividido pelo parâmetro de taxa λ⁻¹ln 2 lambda– minúsculo elevado a menos 1 vezes logaritmo natural de 2.
• Uma mediana de uma distribuição de Weibull com parâmetro de forma k e parâmetro de escala λ lambda– minúsculo é λ(ln 2)^1/k função lambda–minúsculo do logaritmo natural de 2 elevado a 1 sobre k–minúsculo.

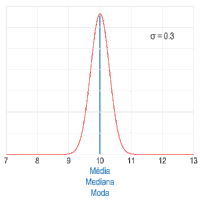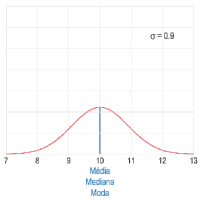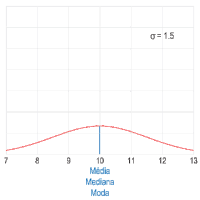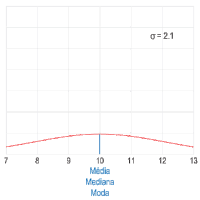
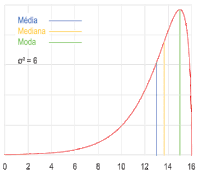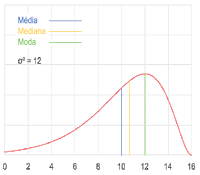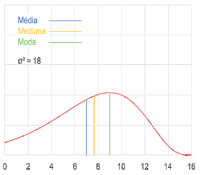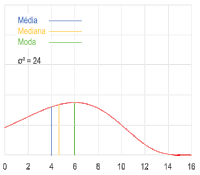
A – Imagem. Ilustração do comportamento das medidas de tendência central em uma distribuição simétrica (por exemplo, uma distribuição normal) quando alterada a dispersão dos dados. A curva vermelha descreve a densidade de probabilidade no espaço amostral e a linha azul representa a localização da média (azul), da mediana (amarelo) e da moda (verde) do conjunto de dados.

B – Imagem. Ilustração do comportamento das medidas de tendência central em uma distribuição assimétrica negativa quando alterada a dispersão dos dados. A curva vermelha descreve a densidade de probabilidade no espaço amostral, a linha azul (à esquerda) representa a média, a linha amarela (ao meio) representa a mediana e a linha verde (à direita) representa a moda do conjunto de dados.

C – Imagem. Ilustração do comportamento das medidas de tendência central em uma distribuição assimétrica positiva (por exemplo, uma distribuição qui-quadrado) quando alterada a dispersão dos dados. A curva vermelha descreve a densidade de probabilidade dos dados no espaço amostral, a linha azul (à direita) representa a média, a linha amarela (ao meio) representa a mediana e a linha verde (à esquerda) representa a moda do conjunto de dado

D – Imagem. Ilustração do comportamento das medidas de tendência central em uma distribuição bimodal, formada por outras duas distribuições com seus respectivos parâmetros, que transita entre distribuição assimétrica positiva, distribuição assimétrica negativa e distribuição simétrica conforme as dispersões dos dados no espaço amostral são alteradas. A curva vermelha descreve a densidade de probabilidade dos dados no espaço amostral, a linha azul representa a média, a linha amarela representa a mediana e a linha verde representa a moda do conjunto de dados.

50 – Populações

51 – Propriedade da otimização

52 – O erro absoluto médio de uma variável real $c$ c–minúsculo com relação a uma variável aleatória $X$ x–maiúsculo é $E(\left|X-c\right|)\,$ esperança e–maiúsculo do módulo de x–maiúsculo menos c–minúsculo, em que $|\cdot |$ módulo é o valor absoluto. Seja $X$ x–maiúsculo uma variável aleatória tal que a esperança $E(\left|X-c\right|)\,$esperança e–maiúsculo do módulo de x–maiúsculo menos c–minúsculo existe. Então, $m$ m–minúsculo é a mediana de $X$ x–maiúsculo se e somente se $m$ m–minúsculo for minimizador do erro absoluto médio com relação à $X$: $m={\mbox{arginf}}_{c\in \mathbb {R} }\ E(\left|X-c\right|)\,$x–maiúsculo m–minúsculo igual a argumento . . . com c–minúsculo pertencente ao conjunto dos números reais r–maiúsculo da esperança e–maiúsculo do módulo de x–maiúsculo menos c–minúsculo. Em particular, $m$ m–minúsculo é a mediana da amostra se e somente se $m$ m–minúsculo for minimizador da média aritmética dos desvios absolutos.

53 – Em termos mais gerais, uma mediana é definida como o minimizador de $E(\left|X-c\right|-\left|X\right|)$ esperança e–maiúsculo de abre parêntesis módulo de x–maiúsculo menos c–minúsculo menos módulo de x–maiúsculo fecha parêntesis, como discutido abaixo na seção sobre medianas multivariadas, especialmente mediana espacial. Essa definição baseada na otimização da mediana é útil em análise de dados estatísticos como no agrupamento de k-medians.

54 – Distribuições unimodais

55 – É possível mostrar para uma distribuição modal que a mediana ${\tilde {X}}$ til sobre x–maiúsculo e a média ${\bar {X}}$ barra sobre x–maiúsculo estão dentro de $({\frac {3}{5}})^{\frac {1}{2}}\approx 0,7746$ 3 sobre 5 elevado a 1 sobre 2 é aproximadamente 0,7746 desvios-padrão de cada uma.

56 – Em símbolos,

${\frac {\left|{\tilde {X}}-{\bar {X}}\right|}{\sigma }}\leq ({\frac {3}{5}})^{\frac {1}{2}}$ módulo de til sobre x–maiúsculo menos barra sobre x–maiúsculo sobre sigma–minúsculo menor ou igual a 3 sobre 5 elevado a 1 sobre 2,

em que ${\frac {\left|{\tilde {X}}-{\bar {X}}\right|}{\sigma }}$ 'módulo de til sobre x–maiúsculo menos barra sobre x–maiúsculo sobre sigma–minúsculo' é o valor absoluto.

57 – Uma relação semelhante é mantida entre a mediana e a moda, que estão dentro de $3^{\frac {1}{2}}\approx 1,732$ 3 elevado a 1 sobre 2 é aproximadamente 1,732 desvios-padrão de cada uma.

58 – Em símbolos,

${\frac {\left|{\tilde {X}}-\mathrm {moda} \right|}{\sigma }}\leq 3^{\frac {1}{2}}$'módulo de til sobre x–maiúsculo menos moda sobre sigma–minúsculo menor ou igual a 3 elevado a 1 sobre 2.'

59 – Desigualdade entre média e mediana

60 – Se a distribuição de probabilidade tiver variância finita, a distância entre a mediana e a média é limitada por um desvio-padrão. Esse limite foi provado por Mallows, que usou a desigualdade de Jensen duas vezes:

$\left|\mu -m\right|=\left|\mathrm {E} (X-m)\right|\leq \mathrm {E} \left(\left|X-m\right|\right)\leq \mathrm {E} \left(\left|X-\mu \right|\right)\leq {\sqrt {\mathrm {E} ((X-\mu )^{2})}}=\sigma .$

módulo de mi–minúsculo menos m–minúsculo igual a módulo da esperança e–maiúsculo de x–maiúsculo menos m–minúsculo menor ou igual a esperança e–maiúsculo do módulo de x–maiúsculo menos m–minúsculo menor ou igual a esperança e–maiúsculo do módulo de x–maiúsculo menos mi–minúsculo menor ou igual a raiz quadrada de esperança e–maiúsculo de x–maiúsculo menos mi–minúsculo elevado a dois Igual a sigma–minúsculo

61 – A primeira e a terceira desigualdade vêm da desigualdade de Jensen aplicada à função de valor absoluto e à função quadrada, ambas convexas. A segunda desigualdade vem da minimização da função de desvio absoluto pela mediana, em que:

$a\mapsto \mathrm {E} (\left|X-a\right|)$ a–minúsculo tende a esperança e–maiúsculo do módulo de x–maiúsculo menos a–minúsculo.

62 – Essa prova pode facilmente ser generalizada para uma versão multivariada da desigualdade:

${\displaystyle \left\|\mu -m\right\|=\left\|\mathrm {E} (X-m)\right\|\leq \mathrm {E} \|X-m\|\leq \mathrm {E} (\left\|X-\mu \right\|)\leq {\sqrt {\mathrm {E} (\|X-\mu \|^{2})}}={\sqrt {\mathrm {trace} (\mathrm {var} (X))}}}$$\left\|\mu -m\right\|=\left\|\mathrm {E} (X-m)\right\|\leq \mathrm {E} \|X-m\|\leq \mathrm {E} (\left\|X-\mu \right\|)\leq {\sqrt {\mathrm {E} (\|X-\mu \|^{2})}}={\sqrt {\mathrm {trace} (\mathrm {var} (X))}}$$\left\|\mu -m\right\|=\left\|\mathrm {E} (X-m)\right\|\leq \mathrm {E} \|X-m\|\leq \mathrm {E} (\left\|X-\mu \right\|)\leq {\sqrt {\mathrm {E} (\|X-\mu \|^{2})}}={\sqrt {\mathrm {trace} (\mathrm {var} (X))}}$,

$\left\|\mu -m\right\|=\left\|\mathrm {E} (X-m)\right\|\leq \mathrm {E} \|X-m\|\leq \mathrm {E} (\left\|X-\mu \right\|)\leq {\sqrt {\mathrm {E} (\|X-\mu \|^{2})}}={\sqrt {\mathrm {trace} (\mathrm {var} (X))}}$norma de mi–minúsculo menos m–minúsculo igual a norma de esperança e–maiúsculo de x–maiúsculo menos m–minúsculo menor ou igual a esperança e–maiúsculo da norma de x–maiúsculo menos m–minúsculo menor ou igual a esperança e–maiúsculo da norma de x–maiúsculo menos mi–minúsculo menor ou igual a raiz quadrada esperança e–maiúsculo da norma de x–maiúsculo menos mi–minúsculo elevado a dois igual a raiz quadrada de traço da variância de x–maiúsculo

em que $m$ m–minúsculo é uma mediana espacial. Isto é, em que $m$ m–minúsculo é um minimizador da função $a\mapsto \mathrm {E} (\left\|X-a\right\|).\,$a–minúsculo tende a esperança e–maiúsculo da norma de x–maiúsculo menos a–minúsculo

63 – A mediana espacial é única quando a dimensão do conjunto de dados é igual ou maior que dois. Uma prova alternativa usa a desigualdade unilateral de Chebyshev, que aparece em uma desigualdade em parâmetros de localização e escala.

64 – Desigualdade de Jensen

65 – A desigualdade de Jensen afirma que para qualquer variável aleatória $X$ x–maiúsculo com esperança finita $E(x)$ e–maiúsculo de x–minúsculo para qualquer função convexa $f$ f–minúsculo:

$f(E(x))\leq E(f(x))$ função f–minúsculo da esperança e–maiúsculo de x–minúsculo menor ou igual a esperança e–maiúsculo da função f–minúsculo de x–minúsculo

66 – Se $X$ x–minúsculo é uma variável real com uma mediana única $m$ m–minúsculo e $f$ f–minúsculo é uma função $C$ c–maiúsculo . Então:

$f(m)\leq \operatorname {Mediana} (f(x))$. função f–minúsculo de m–miúsculo menor ou igual a mediana da função f–maiúsculo de x–minúsculo

67 – Uma função $C$ c–maiúsculo é uma função real definida no conjunto dos números reais $\mathbb {R}$ r–maiúsculo , sendo que para qualquer $t$ t–minúsculo real:

$f^{-1}((-\infty ,t])=\{x\in R\mid f(x)\leq t\}$ função inversa f–minúsculo elevado a menos 1 de menos infinito t–minúsculo igual a abre chaves de x–minúsculo pertencente a r–maiúsculo tal que função f–minúsculo de x–minúsculo menor ou igual t–minúsculo

é um intervalo fechado, um singleton ou um conjunto vazio.

68 – Cálculo para grandes amostras

69 – Embora os $n$ n–minúsculo itens de algoritmo de ordenação requerem O(n log n) o–maiúsculo n–minúsculo logaritimo de n–minúsculo operações, algoritmos de seleção podem computar o menor k-ésimo de $n$ n–minúsculo itens com apenas O(n) função o–maiúsculo de n–minúsculo operações. Isso inclui a mediana, a $n/2$ n–minúsculo sobre 2 ésima ordem estatística (ou para um número par de amostrar, a média das duas ordens estatísticas médias).

70 – Os algoritmos de seleção também tem a desvantagem de requerer uma memória O(n) função o–maiúsculo de n–minúsculo, que significa que eles precisam ter a memória da amostra inteira ou da porção de tamanho linear da amostra. Como o requisito da memória pode ser restritivo (assim como o requisito do tempo linear), vários procedimentos de estimativa para a mediana tem sido desenvolvidos.

71 – Um procedimento de estimativa simples é a mediana de regra três, que estima a mediana como a mediana de uma subamostra de três elementos. Seja $A$ a–maiúsculo uma amostra com elementos $A[i],i=1,\dots ,n$ a–maiúsculo de i–minúsculo com i–minúsculo igual a 1 e assim sucessivamente até n–minúsculo. Então

$med3(A)=mediana(A[1],A[n/2],A[n])$ mediana de uma subamostra de três elementos de a–maiúsculo med–3–de–a–maiúsculo igual a mediana de a–maiúsculo abre colchete 1 fecha colchete, a–maiúsculo abre colchete n–minúsculo sobre 2 fecha colchete a–minúsculo abre colchete n–minúsculo fecha colchete.

72 – Isso é comumente usada como uma subrotina do algoritmo de classificação quicksort, que usa uma estimativa da mediana de input. Uma estimativa mais robusta é a nona deTukey, a mediana de regra três aplicada com recurso limitado:

$nona(A)=med3(med3(A[1,...,n/3]),med3(A[n/3+1,...,2n/3]),med3(A[2n/3+1,...,n]))$.

nona de a–maiúsculo igual a mediana de uma subamostra de três elementos med–3 da mediana de uma subamostra de três elementos med–3 a–maiúsculo abre colchetes 1 e assim sucessivamente até n–minúsculo sobre 3 fecha colchetes mediana de uma subamostra de três elementos med–3 de a–maiúsculo abre colchete n–minúsculo sobre 3 mais 1 e assim sucessivamente até 2 n–minúsculo sobre 3 fecha colchete mediana de uma subamostra de três elementos med–3 de a–maiúsculo abre colchete 2 n–minúsculo sobre 3 mais 1 e assim sucessivamente até n–minúsculo fecha colchete

73 – Por exemplo, temos uma amostra $A$ a–maiúsculo com elementos $A=\{8,5,1,7,12,3,2,9,15\}$ a–maiúsculo igual a abre chaves 8, 5, 1, 7, 12, 3, 2, 9,15 fecha chaves Então

$med3(A[1,2,3])=mediana(8,5,1)=5$, 'mediana da subamostra de três elementos med–3 de a–maiúsculo abre colchete 1, 2, 3 fecha colchete igual a mediana de 8, 5, 1 igual a 5'

$med3(A[4,5,6])=mediana(7,12,3)=7$, 'mediana da subamostra de três elementos med–3 de a–maiúsculo abre colchete 4, 5, 6 fecha colchete igual a mediana de 7, 12, 3 igual a 7'

$med3(A[7,8,9])=mediana(2,9,15)=9$, 'mediana da subamostra de três elementos med–3 de a–maiúsculo abre colchete 7, 8, 9 fecha colchete igual a mediana de 2, 9, 15 igual a 9'

e

$nona(A)=mediana(5,7,9)=7$. nona de a–maiúsculo igual a mediana de 5, 7, 9 igual a 7

74 – Esse estimador "re–mediana" requer um tempo linear e uma memória sublinear, operando em uma única passagem sobre a amostra.

75 – Distribuição de mediana amostral

76 – A distribuição tanto da média da amostra quanto da mediana da amostra foram determinadas por Laplace. A distribuição da mediana da amostra de uma população com uma função densidade $f(x)$ f–minúsculo de x–minúsculo é assintoticamente normal com média $m$ m–minúsculo e variância

${\frac {1}{4nf(m)^{2}}}$, 1 sobre 4 vezes n–minúsculo vezes função f–minúsculo de m–minúsculo elevado a dois

em que $m$ m–maiúsculo é o valor médio da distribuição e $n$ é o tamanho da amostra. Na prática, $f(m)={\frac {1}{2}}$ função f–minúsculo de 1 sobre 2 por definição.

77 – Os resultados também têm sido estendidos. É sabido que para o $p$–ésimo quantil a distribuição da $p$–ésima amostra é assintoticamente normal em torno do $p$–ésimo quantil com variância igual a

${\frac {p(1-p)}{nf(x_{p})^{2}}}$, razão de p–minúsculo abre parêntesis 1 menos p–minúsculo fecha parênteses por n–minúsculo vezes a função f–minúsculo de x–minúsculo subscrito p–minúsculo elevado a dois

em que $f(x_{p})$ a função f–minúsculo de x–minúsculo subscrito p–minúsculo é o valor da densidade de distribuição no $p$–ésimo quantil.

78 – No caso de uma variável discreta, a distribuição da amostra da mediana para pequenas amostras pode ser estudada da seguinte maneira. Seja um tamanho de amostra com número ímpar de elementos $N=2n+1$ n–maiúsculo igual a 2 n–minúsculo igual a 1 Se um dado valor $v$ v–minúsculo for a mediana da amostra, então duas condições devem ser satisfeitas.

• No máximo, $n$ n–minúsculo observações podem ter valor igual ou menor que $v-1$ v–minúsculo menos 1.
• No mínimo, $n+1$ n–minúsculo mais 1 observações devem ter valor igual ou menor que $v$ v–minúsculo.

79 – Seja $i$ i–minúsculo o número de observações com valor igual ou menor que $v-1$ v–minúsculo menos 1. Seja $j$ j–minúsculo o número de observações com valor exato $v$ v–minúsculo. Então, $i$ i–minúsculo tem valor mínimo 0 e valor máximo $n$ n–minúsculo, enquanto $j$ j–minúsculo tem valor mínimo $n+1-i$ n–minúsculo mais 1 menos i–minúsculo (para totalizar pelo menos $n+1$ n–minúsculo mais 1 observações) e valor máximo $2n+1-i$ 2 n–minúsculo mais 1 menos i–minúsculo (para totalizar pelo menos $2n+1$ 2 n–minúsculo mais 1 observações).

80 – Se uma observação tem valor menor ou maior que $v$, não é relevante quão abaixo ou acima de $v$ v–minúsculo é o valor. Logo, é possível representar as observações pela distribuição trinomial com probabilidades $F(v-1)$ função f–maiúsculo de v–minúsculo menos 1 , $f(v)$ função f–minúsculo de v–minúsculo' e $1-F(v)$ 1 menos função f–maiúsculo de v–minúsculo'. Portanto, a probabilidade de a mediana $m$ m–minúsculo ter valor $v$ v–minúsculo é dada por:

$P(m=v)=\sum _{i=0}^{n}\sum _{j=n+1-i}^{2n+1-i}{\frac {(2n+1)!}{i!j!(2n+1-i-j)!}}[F(v-1)]^{i}[f(v)]^{j}[1-F(v)]^{2n+1-i-j}.$

função de probabilidade p–maiúsculo de m–minúsculo igual a v–minúsculo igual a somatória com i–minúsculo igual a 0 até n–minúsculo vezes a somatória com j–minúsculo igual n–minúsculo mais 1 menos i–minúsculo até até 2 n–minúsculo mais 1 menos i–minúsculo da razão de dois n–minúsculo mais 1 fatorial sobre i–minúsculo fatorial vezes j–minúsculo fatorial vezes abre parêntesis 2 n–minúsculo mais 1 menos i–minúsculo menos j–minúsculo fecha parêntese fatorial.

81 – Somar isso a todos os valores $v$ v–minúsculo define uma distribuição apropriada e fornece uma soma unitária. Embora a função $f(v)$ f–minúsculo de v–minúsculo geralmente não será conhecida, poderá ser estimada de uma distribuição de frequência observada. É o exemplo da tabela seguinte. Embora a distribuição atual não seja conhecida, a amostra de 3.800 observações permite uma avaliação suficientemente precisa de $f(v)$ função f–minúsculo de v–minúsculo.

v	0	0.5	1	1.5	2	2.5	3	3.5	4	4.5	5
f(v)	0.000	0.008	0.010	0.013	0.083	0.108	0.328	0.220	0.202	0.023	0.005
F(v)	0.000	0.008	0.018	0.031	0.114	0.222	0.550	0.770	0.972	0.995	1.000

82 –Tabela.

Para valor v–minúsculo igual a 0, função f–minúsculo de v–minúsculo igual a 0 e função f–maiúsculo de v–minúsculo igual a 0.

Para valor v–minúsculo igual a 0,5, função f–minúsculo de v–minúsculo igual a 0,008 e função f–maiúsculo de v–minúsculo igual a 0,008.

Para valor v–minúsculo igual a 1, função f–minúsculo de v–minúsculo igual a 0,010 e função f–maiúsculo de v–minúsculo igual a 0,018.

Para valor v–minúsculo igual a 1,5, função f–minúsculo de v–minúsculo igual a 0,013 e função f–maiúsculo de v–minúsculo igual a 0,031.

Para valor v–minúsculo igual a 2, função f–minúsculo de v–minúsculo igual a 0,083 e função f–maiúsculo de v–minúsculo igual a 0,114.

Para valor v–minúsculo igual a 2,5, função f–minúsculo de v–minúsculo igual a 0,108 e função f–maiúsculo de v–minúsculo igual a 0,222.

Para valor v–minúsculo igual a 3, função f–minúsculo de v–minúsculo igual a 0,328 e função f–maiúsculo de v–minúsculo igual a 0,550.

Para valor v–minúsculo igual a 3,5, função f–minúsculo de v–minúsculo igual a 0,220 e função f–maiúsculo de v–minúsculo igual a 0,770.

Para valor v–minúsculo igual a 4, função f–minúsculo de v–minúsculo igual a 0,202 e função f–maiúsculo de v–minúsculo igual a 0,972.

Para valor v–minúsculo igual a 4,5, função f–minúsculo de v–minúsculo igual a 0,023 e função f–maiúsculo de v–minúsculo igual a 0,995.

Para valor v–minúsculo igual a 5, função f–minúsculo de v–minúsculo igual a 0,005 e função f–maiúsculo de v–minúsculo igual a 1.

83 – Com os dados é possível investigar o efeito do tamanho da amostra nos erros padrões da média e da mediana. A média observada é 3,16. A mediana bruta é 3 e a mediana interpolada observada é 3,174. A tabela seguinte fornece algumas estatísticas de comparação. O erro padrão da mediana é dado tanto da expressão $P(m=v)$ função probabilidade p–maiúsculo de m–minúsculo igual a v–minúsculo quanto da aproximação assintótica dadas anteriormente.

TAMANHO DA AMOSTRA	3	9	15	21
Valor esperado da mediana	3.198	3.191	3.174	3.161
Erro padrão da mediana	0.482	0.305	0.257	0.239
Erro padrão da mediana (aproximação assintótica)	0.879	0.508	0.393	0.332
Erro padrão da média	0.421	0.243	0.188	0.159

84 – Tabela.

Para tamanho da amostra 3, valor esperado da mediana é igual a 3,198, erro padrão da mediana é igual a 0,482, erro padrão da mediana (aproximação assintótica) é igual a 0,879 e erro padrão da média é igual a 0,421.

Para tamanho da amostra 9, valor esperado da mediana é igual a 3,191, erro padrão da mediana é igual a 0,305, erro padrão da mediana (aproximação assintótica) é igual a 0,508 e erro padrão da média é igual a 0,243.

Para tamanho da amostra 15, valor esperado da mediana é igual a 3,174, erro padrão da mediana é igual a 0,257, erro padrão da mediana (aproximação assintótica) é igual a 0,393, erro padrão da média é igual a 0,188.

Para tamanho da amostra 21, valor esperado da mediana é igual a 3,161, erro padrão da mediana é igual a 0,239, erro padrão da mediana (aproximação assintótica) é igual a 0,332 e erro padrão da média é igual a 0,159.

85 – O valor esperado da mediana diminui ligeiramente à medida que a medida da amostra aumenta. Já que os erros padrão tanto da média quanto da mediana são proporcionais à raiz quadrada inversa do tamanho da amostra.

86 – No caso de uma variável contínua, o argumento seguinte pode ser usado. Se um dado valor $v$ for a mediana, então uma observação precisa assumir o valor $v$. A probabilidade elementar é $f(v)dv$ função f–minúsculo de v–minúsculo vezes diferencial d–minúsculo v–minúsculo. Então, $n$ n–minúsculo das $2n$ 2 n–minúsculo observações precisam ser maiores que $v$ v–minúsculo e as outras $n$ n–minúsculo das $2n$ 2 n–minúsculo observações precisam ser menores que $v$ v–minúsculo. A probabilidade é o $n$-ésimo termo de uma distribuição binomial com parâmetros $F(v)$ função f–minúsculo de v–minúsculo e $2n$ 2 n–minúsculo.

87 – Multiplica-se por $2n+1$ 2 n–minúsculo mias 1 porque qualquer uma das observações na amostra pode ser a mediana da observação. Então, a probabilidade elementar da mediana no ponto $v$ v–minúsculo é dada por:

$f(v){\frac {(2n)!}{n!n!}}[F(v)]^{n}[1-F(v)]^{n}(2n+1)\,dv.$ função f–minúsculo de v–minúsculo vezes a razão de 2 n–minúsculo fatorial por n–minúisculo fatorial vezes n–minúsculo fatorial vezes abre colchetes função f–maiúsculo de v–minúsculo fecha colchetes elevado a n–minúsculo vezes abre colchetes 1 menos função f–maiúsculo de v–minúsculo fecha colchetes elevado a n–minúsculo vezes sbre parêntesis 2 n–minúsculo mais 1 fehca parêntesis vezes a diferencial d–minúsculo v–minúsculo

88 – Introduz-se a função beta. Para os argumentos inteiros $\alpha$ alpha–minúsculo e $\beta$ beta–minúsculo, pode-se expressar $\mathrm {B} (\alpha ,\beta )=(\alpha -1)!(\beta -1)!/(\alpha +\beta -1)!$ função b–maiúsculo de alpha–minúsculo beta–minúsculo igual razão de abre parênteses alpha–minúsculo menos 1 fecha parênteses fatorial vezes abre parênteses beta–minúsculo menos 1 fecha parênteses fatorial por abre parênteses alpha–minúsculo mais beta–minúsculo menos um fecha parêntesis fatorial. Também, nota-se que $f(v)=dF(v)/dv$ função f–minúsculo de v–minúsculo igual a diferencial da função f–maiúsculo de v–minúsculo sobre diferencial d–minúsculo v–minúsculo.. Usando as relações anteriores e igualando $\alpha$ alpha–minúsculo e $\beta$ beta–minúsculo a $(n+1)$ n–minúsculo mais 1 permite-se que a última expressão seja escrita como

${\frac {[F(v)]^{n}[1-F(v)]^{n}}{\mathrm {B} (n+1,n+1)}}\,dF(v)$. razão de abre colchetes função de f–maiúsculo de v–minúsculo fecha colchetes elevado a n–minúsculo vezes abre colchetes 1 menos função f–maiúsculo de v–minúsculo fecha colchetes elevado a n–minúsculo por b–maiúsculo de abre parêntesis de n–minúsculo mais 1 n–minúsculo mais 1 fecha parêntesis vezes diferencial d–minúsculo da função f–maiúsculo de v–minúsculo

89 – Então, a função densidade da mediana é uma distribuição $\beta$ beta–minúsculo simétrica sobre o intervalo da unidade que suporta $F(v)$ a função f–maiúsculo de v–minúsculo. A média é 0,5 e o desvio-padrão (erro padrão da mediana da amostra) é $1/(2{\sqrt {N+2}})$ 1 sobre 2 vezes raiz quadrada de n–maiúsculo mais 2. Tais condições apenas podem ser usadas se $f(v)$ função f–minúsculo de v–minúsculo for conhecido ou puder ser assumido, $f(v)$ função f–minúsculo de v–minúsculo pode ser integrado para encontrar $F(v)$ função f–maiúsculo de v–minúsculo e $F(v)$ função f–maiúsculo de v–minúsculo pode ser invertido, o que nem sempre será o caso. Mesmo quando for o caso, os pontos de corte para $f(v)$ função f–minúsculo de v–minúsculo podem ser calculados diretamente sem recurso para a distribuição na mediana no intervalo da unidade. Embora seja interessante na teoria, o resultado não é muito útil na prática.

90 – Estimativa da variância a partir de dados da amostra

91 – O valor $(2f({\displaystyle \nu }))^{-2}$ 2 vezes função de f–minúsculo de v–minúsculo elevado a menos 2 — que é o valor assintótico de $n^{-{\frac {1}{2}}}(\nu -m)$ n–minúsculo elevado menos a 1 sobre 2 vezes v–minúsculo menos m–minúsculo, quando tamanho da amostra $n\to \infty$ n–minúsculo tende ao infinito, em que $\nu$ v–minúsculo é a mediana da população — tem sido estudado por diferentes autores. O método jackknife delete one padrão produz resultados inconsistentes. O método delete $k$ — em que $k$ k–minúsculo aumenta com o tamanho da amostra — tem mostrado ser uma alternativa assintoticamente consistente apesar de computacionalmente cara para grandes conjuntos de dados. Uma estivativa bootstrap é conhecida por ser consistente, mas converge muito lentamente (ordem de $n^{-{\frac {1}{4}}}$n–minúsculo elevado a menos 1 sobre 4). Outras alternativas têm sido propostss, proém seus comportamentos podem diferir entre pequenas e grandes amostras.

92 – Eficiência

93 – Medida como a razão entre a variância da média e a variância da mediana, a eficiência da mediana da amostra depende do tamanho da amostra e da distribuição da população subjacente. Para uma amostra de tamanho $2n+1$ 2 n–minúsculo mais 1 de uma distribuição normal, a razão é

${\frac {4n}{\pi (2n+1)}}$. 4 n–minúsculo sobre pi vezes abre parêntesis 2 n–minúsculo mais 1 fecha parêntesis

94 – Para grandes amostras ($n\to \infty$ n–minúsculo tendendo ao infinito), a razão tende a ser

${\frac {2}{\pi }}$. dois sobre pi

93 – Outros estimadores

94 – Para distribuições univariadas que são simétricas em relação a uma mediana, o estimador de Hodges–Lehmann é um estimador altamente eficiente e robusto da mediana da população.

95 – Se os dados forem representados por um modelo estatístico especificando uma família particular de distribuições de probabilidade, então estimativas da média podem ser obtidas ajustando a família de distribuições de probabilidade e calculando a mediana teórica da distribuição ajustada. A interpolação de Pareto é uma aplicação disso quando a população é assumida como tendo um princípio de Pareto.

96 – Coeficiente de dispersão

97 – O coeficiente de dispersão (CD c–maiúsculo d–maiúsculo) é definida como a razão entre o desvio médio absoluto da mediana e a mediana dos dados. É uma medida estatística usada pelos estados norte-americanos de Iowa, Nova Iorque e Dakota do Sul em estimativa de impostos.

Em símbolos,

$CD={\frac {1}{n}}{\frac {\sum |m-x|}{m}}$, coeficiente de dispersão CD c–maiúsculo d–maiúsculo igual a 1 sobre n–minúsculo vezes somatória do módulo de m–minúsculo menos x–minúsculo sobre m–minúsculo

em que $n$ n–minúsculo é o tamanho da amostra, $m$ m–minúsculo é a mediana da amostra e $x$ é a variável. A soma é tomada em toda a amostra. Intervalo de confiança para coeficiente de dispersão quando tamanho da amostra é grande foi derivado por Bonett e Seier.

98 – Mediana multivariada

99 – Até agora foi discutida mediana univariada, quando a amostra ou a população possuem uma dimensão. Quando a dimensão é igual ou maior que dois, há múltiplos conceitos que ampliam a definição de mediana univariada. Cada uma das medianas multivariadas concorda com uma mediana univariada quando a dimensão é exatamente um.

100 – Mediana marginal

101 – A mediana marginal é definida para vetores definidos em relação a um conjunto fixo de coordenadas. A mediana marginal é definida como o vetor, cujos componentes medianas univariadas. A mediana marginal é fácil de computar, e suas propriedades foram estudadas por Puri e Sen.

102 – Mediana espacial

103 – Para $N$ n–maiúsculo vetores em um espaço normado, a media espacial minimiza a distância média

$a\mapsto {\frac {1}{N}}\sum _{n}{(\left\|x_{n}-a\right\|)},\,$a–minúsculo tende a 1 sobre n–maiúsculo vezes somatória de n–minúsculo da norma de x–minúsculo subscrito n–minúsculo menos a–minúsculo

em que $x_{n}$ x–minúsculo subscrito n–minúsculo e $a$ a–minúsculo são vetores.

104 – A mediana espacial é única quando a dimensão do conjunto de dados é igual ou maior que dois e a norma é euclidiana (or outra norma estritamente convexa). A mediana espacial também é chamada mediana L1 l–minúsculo 1, mesmo quando a norma é euclidiana. Outros nomes são usados especialmente para conjuntos finitos de pontos como mediana geométrica, ponto de Fermat (em mecânica), ponto de Weber ou Fermat-Weber (na teoria da localização geográfica).

105 – Mais genericamente, uma mediana espacial é definida como minimizador de:

$a\mapsto {\frac {1}{N}}\sum _{n}{(\|x_{n}-a\|-\|x_{n}\|)}\,$.'a–minúsculo tende a 1 sobre n–maiúsculo vezes somatória de n–minúsculo da norma de x–minúsculo subscrito n–minúsculo menos a–minúsculo menos a norma de x–minúsculo subscrito n–minúsculo'.

106 – A definição geral é conveniente para definir uma mediana espacial de uma população em um espaço normal de dimensão finita como para distribuições com uma média finita. Medianas espaciais são definidas por vetores aleatórios com valores no espaço de Banach. A mediana espacial é um estimador altamente robusto e eficiente da tendência central de uma população.

107 – Outras medianas multivariadas

108 – Uma generalização alternativa da mediana espacial em dimensões maiores que não tem relação com uma métrica particular é o centerpoint (geometria).

109 – Outros conceitos relacionados a mediana

110 – Mediana interpolada

111 – Para variáveis discretas, às vezes é útil considerar os valores observados como sendo pontos médios de intervalos contínuos subjacentes. Um exemplo é a escala Likert, em que opiniões ou preferências são expressas em uma escala com um conjunto de números de respostas possíveis.

112 – Se a escala consiste de números inteiros positivos, uma observação do número 3 pode ser considerada como o intervalo entre 2,50 e 3,50. É possível estimar a mediana da variável subjacente. Seja que 22% das observações tenham valor igual ou inferior que 2. Seja que 55% das observações tenham valor igual ou inferior que 3. Então, 33% das observações tem valor igual a 3. Logo, a mediana $m$ m–minúsculo é 3 porque é o menor valor de $x$ x–minúsculo para o qual $F(x)$ função f–maiúsculo de x–minúsculo é maior que a metade.

113 – Entretanto, a mediana interpolada é um lugar entre 2,50 e 3,50. É adicionada metade da largura do intervalo $w$ à mediada para ter o limite superior do intervalo da mediana. É subtraída a proporção da largura do intervalo que é igual a proporção de 33% acima da marca de 50%. Em outras palavras, são divididos os 33% em 28% abaixo da mediana e 5% acima da mediana e é subtraído os ${\frac {5}{33}}$ 5 sobre 33 da largura do intervalo do limite superior de 3,50 para resultar em uma mediana interpolada de 3,35.

114 – Mais formalmente, a mediana interpolada pode ser calculada a partir de:

$m_{\text{int}}=m+w\left[{\frac {1}{2}}-{\frac {F(m)-1/2}{f(m)}}\right]$. m–minúsculo subscrito int igual a m–minúsculo mais w–minúsculo vezes abre colchetes 1 sobre 2 menos razão de função f–maiúsculo de m–minúsculo menos 1 sobre 2 por função f–minúsculo de m–minúsculo fecha colchetes.

115 – Pseudo-mediana

116 – Para distribuições univariadas que são simétricas em torno de uma média, o estimador de Hodges-Lehmann é um estimador altamente eficiente e robusto da população da mediana para distribuições não simétricas. O estimador de Hodges-Lehmann também é um estimador altamente eficiente e robusto da população da pseudo-mediana, a mediana de uma distribuição simétrica a qual é próxima da população da mediana. O estimador de Hodges-Lehmann tem sido generalizado para distribuições multivariadas.

117 – Variantes de regressão

118 – O estimador de Theil-Sen é um método para uma regressão linear robusta, baseado em mediana encontradas em declives.

119 – Filtro da mediana

120 – Em processamento de imagens raster monocromáticos, há um ruído conhecido como ruído impulsivo quando cada pixel fica independentemente branco ou preto (como alguma pouca probabilidade). Uma imagem construída de mediana de valores de vizinhos mais próximos (como um quadrado 3X3) pode efetivamente reduzir o ruído.

121 – Clustering

122 – Em clustering, o agrupamento k-medians fornece uma definição de cluster, na qual o critério de maximização da distância entre cluster–medias usado no agrupamento k-means é substituído pela maximização da distância entre cluster–medianas.

123 – Linha média–mediana

124 – É um método da regressão robusta. A ideia foi concebida em 1940 por Abraham Wald, que sugeriu dividir um conjunto de dados bivariados em duas metades, dependendo do valor do parâmetro independente $x$ x–minúsculo. A metade da esquerda teria valores menores que a mediana e a metade da direita teria valores maiores que a média. Wald sugeriu tomar as médias da variável dependente $y$ y–minúsculo e da variável independente $x$ x–minúsculo da metade da direita e da metade da esquerda e estimar o declive da linha juntando esses dois pontos.

125 – Uma ideia similar foi sugerida em 1942 por Nair and Shrivastava, que preferiram dividir a amostra em três partes iguais antes de calcular as médias das subamostras. Em 1951, Brown e Mood propuseram a ideia de usar as medianas em vez de usar as médias de duas subamostras. Tukey combinou as ideias e recomendou dividir a amostra em três subamostras com tamanhos iguais e estimar a linha com base nas medianas das subamostras.

126 – Estimadores não enviesados pela mediana

127 – Um estimador não enviesado pela média minimiza o risco (perda esperada) relacionada à função de perda do erro quadrático, como observado por Gauss. Um estimador não enviesado pela mediana minimiza o risco relacionado a função de perda do desvio absoluto, com observado por Laplace.

128 – Há outras funções de perda que são usadas na teoria estatística, particularmente na estatística robusta. A teoria dos estimadores não enviesados pela mediana foi reavivada por George W. Brown em 1947:

129 – Citação.

“ É dito que uma estimativa de um parâmetro unidimensional θ não será enviesada pela mediana se, para um θ fixo, a mediana da distribuição da estimativa está no valor θ. Isto é, a mediana da distribuição subestima apenas tantas vezes quanto superestima. Esse requisito parece para a maioria dos propósitos satisfazer tanto quanto o requisito não enviesado pela média e tem a propriedade adicional de ser invariante sob a transformação um–para–um. ”

130 – Mais propriedades dos estimadores não enviesados pela mediana tem sido reportados. Estimadores não enviesados pela mediana são invariantes sob transformações um–para–um.

131 – Há métodos de construção de estimadores não enviesados pela mediana que são ideais (no sentido análogo à propriedade da variância mínima considerada para estimadores não enviesados pela mediana). Tais construções existem para distribuições de probabilidade com funções da verossimilhança monótonas.

132 – Tal procedimento é análogo o procedimento de Rao–Blackwell para estimadores não enviesados pela média: o procedimento é válido para uma pequena classe de distribuições de probabilidade que realiza o procedimento de Rao–Blackwell, mas para uma classe maior de funções de perda.

133 – Fim da gravação. Materiais adicionais como notas, referências, bibliografias e ligações externas estão disponíveis no artigo original escrito na Wikipédia.

134 – Texto narrado pelo usuário Mariliawikipedia pelo Centro de Pesquisa, Inovação e Difusão em Neuromatemática, com i apoio da Fundação de Amparo à Pesquisa do Estado de São Paulo, para a Wikipédia lusófona. Este áudio está licenciado sob Creative Commons Attribution ShareAlike 4.0 Unported.

135 – Índice

1História 2Conceitos básicos 3Cálculos básicos 4Exemplos 4.1População com número de elementos ímpar 4.2População com número de elementos par 5Medida de tendência central 5.1Mediana para dados ordenados 6Distribuições de probabilidade 6.1Medianas de distribuições particulares 7Propriedades 7.1Propriedade da otimização 7.2Distribuições unimodais 7.3Desigualdade entre média e mediana 7.4Desigualdade de Jensen 7.5Cálculo para grandes amostras 7.6Distribuição de mediana amostral 7.7Estimativa da variância a partir de dados da amostra 7.8Eficiência 7.9Outros estimadores 7.10Coeficiente de dispersão 8Mediana multivariada 8.1Mediana marginal 8.2Mediana espacial 8.3Outras medianas multivariadas 9Outros conceitos relacionados a mediana 9.1Mediana interpolada 9.2Pseudo-mediana 9.3Variantes de regressão 9.4Filtro da mediana 9.5Clustering 9.6Linha média–mediana 10Estimadores não viesados pela mediana

Ver também

• Decil
• Quartil
• Percentil
• Desvio absoluto
• Função Lipschitz contínua
• Moda