Nomografia

Nomograma para calcular resistências em paralelo.

A nomografia, termo cunhado pelo matemático francês Maurice d'Ocagne a partir do grego nomos, lei, e graphein, escrita, é um processo de cálculo pelo qual a relação entre duas ou mais variáveis é representada por um sistema de linhas e pontos, e resolvida através de uma construção geométrica simples.

O nomograma traduz e resolve a fórmula ou equação entre as variáveis.

Representação gráfica correspondente a uma interpretação geométrica de funções que permite resolver equações ou interpolações.

Exemplo

Nomograma para resolver a equação x + y + z = 0

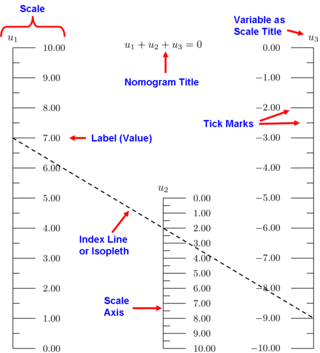
Seja, por exemplo, a relação entre três variáveis x, y e z dada por:

$x+y+z=0\,$

Pela geometria analítica, esta equação representa um plano que corta cada plano coordenado em sua uma de suas bissetrizes. A solução, pela nomografia, consiste em desenhar duas linhas retas e marcar, nelas, os valores respectivamente de x e y, em seguida, em desenhar uma outra linha entre estas, e marcar, nesta linha, os valores de z. Esta marcação é feita ligando-se os valores de x e os de y através de uma linha, e obtendo o ponto de interseção desta linha com a linha dos z.

O gráfico ou carta de Smith mostra a relação existente entre a impedância de uma linha de transmissão eletromagnética e sua longitude.

Abrangência

Toda equação de duas varíaveis pode ser resolvida através da nomografia.

David Hilbert, que conhecia a solução de Maurice d'Ocagne para a equação do sétimo grau, através de elementos móveis, propôs, como seu décimo-terceiro problema, que se demonstrasse que a equação genérica do sétimo grau não pudesse ser resolvida com a ajuda de funções contínuas de uma variável, ou seja, a equação não seria resolvida através da nomografia.^{[carece de fontes]}

O problema foi resolvido por Andrei Kolmogorov e Vladimir Arnold, em 1957, que demonstraram uma forma ainda mais genérica da proposta, a saber:

Seja f uma função contínua em várias variáveis. Então f pode ser escrita através de uma composição finita de funções contínuas de uma única variável e a operação binária de adição.