Deconvolução

Deconvolução de uma imagem astronômica. Antes e depois da desconvolução de uma imagem da cratera lunar Copérnico usando o algoritmo Richardson-Lucy.

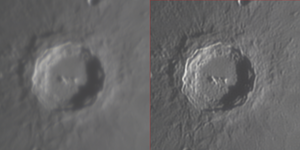
A deconvolução é uma técnica fundamental em diversos campos, desde a ciência de dados até a astronomia e a medicina. Esse processo desempenha um papel crucial na recuperação de sinais ou imagens distorcidas por um sistema, restaurando sua forma original tanto quanto possível.

Em termos simples, a deconvolução é o processo de reverter os efeitos de uma operação de convolução. A convolução é um operador matemático que combina duas funções para produzir uma terceira função, que representa a maneira como uma é afetada pela outra. Pode ser pensada como uma espécie de "mistura" ou "borramento" de informações.

Na prática, a convolução é frequentemente usada em sistemas onde o sinal é distorcido de alguma forma. Por exemplo, em imagens médicas, o sinal pode ser distorcido pela propagação da luz através dos tecidos do corpo. Em sistemas de comunicação, o sinal pode ser distorcido pelo ruído ou por características do canal de transmissão.

A deconvolução entra em cena para tentar recuperar o sinal original, removendo ou reduzindo os efeitos da convolução.

Descrição

Na matemática, deconvolução é o inverso da convolução. Ambas as operações são utilizadas no processamento de sinais e imagens. Por exemplo, pode ser possível recuperar o sinal original após a aplicação de um filtro (convolução) utilizando um método de deconvolução com um certo grau de precisão. Devido ao erro de medição do sinal ou imagem registrado, pode-se demonstrar que quanto pior for a relação sinal-ruído (SNR), pior será a reversão de um filtro; portanto, inverter um filtro nem sempre é uma boa solução, pois o erro se amplifica. A deconvolução oferece uma solução para esse problema.

As bases para a deconvolução e análise de séries temporais foram amplamente estabelecidas por Norbert Wiener do Massachusetts Institute of Technology em seu livro "Extrapolation, Interpolation, and Smoothing of Stationary Time Series" (1949). O livro foi baseado no trabalho que Wiener havia feito durante a Segunda Guerra Mundial, mas que estava classificado na época. Algumas das primeiras tentativas de aplicar essas teorias foram nos campos de previsão do tempo e economia.

Em geral, o objetivo da deconvolução é encontrar a solução f de uma equação de convolução da forma:

$(f\;*\;g)(x)=h(x)=\int _{-\infty }^{\infty }f(u)\cdot g(x-u)\;du\quad (1a)$

Normalmente, h é algum sinal registrado, e f é algum sinal que desejamos recuperar, mas que foi convolucionado com um filtro ou função de distorção g, antes de ser registrado. Normalmente, h é uma versão distorcida de f e a forma de f não pode ser facilmente reconhecida a olho nu ou por operações temporais mais simples. A função g representa a resposta ao impulso de um instrumento ou uma força motriz que foi aplicada a um sistema físico. Se conhecemos g, ou pelo menos conhecemos a forma de g, então podemos realizar deconvolução determinística. No entanto, se não conhecemos g antecipadamente, então precisamos estimá-lo. Isso pode ser feito utilizando métodos de estimação estatística ou construindo os princípios físicos do sistema subjacente, como as equações de circuito elétrico ou equações de difusão.

Existem várias técnicas de deconvolução, dependendo da escolha do erro de medição e dos parâmetros de deconvolução.

Métodos de Deconvolução

A imagem de THz de alta resolução é alcançada pela deconvolução da imagem de THz e da PSF de THz modelada matematicamente. (a) Imagem de THz de um circuito integrado (IC) antes da melhoria; (b) PSF de THz modelada matematicamente; (c) Imagem de THz de alta resolução, que é alcançada como resultado da deconvolução da imagem de THz mostrada em (a) e da PSF mostrada em (b); (d) A imagem de raio-X de alta resolução confirma a precisão dos valores medidos.

Existem várias abordagens para a deconvolução, cada uma com suas próprias vantagens e limitações. Alguns dos métodos mais comuns incluem:

1. Deconvolução Cega: Neste método, não se conhece explicitamente a função de convolução. Em vez disso, tenta-se estimar tanto a função de convolução quanto o sinal original iterativamente.

2. Deconvolução Wiener: Este método assume que tanto o sinal original quanto a função de convolução são estocásticos e tenta minimizar o erro médio quadrático entre a saída deconvoluída e o sinal original.

3. Deconvolução não Linear: Este método utiliza algoritmos não lineares para tentar estimar tanto a função de convolução quanto o sinal original. Métodos como o algoritmo Richardson-Lucy são amplamente utilizados nesse contexto.

4. Deconvolução Espectral: Este método explora as propriedades do espectro de Fourier do sinal e da função de convolução para realizar a deconvolução no domínio da frequência.

Aplicações

Deconvolução

A deconvolução tem uma ampla gama de aplicações em várias áreas:

1. Imagens Médicas: Em técnicas de imagem como a microscopia confocal, a deconvolução é usada para melhorar a resolução e a qualidade das imagens, removendo distorções introduzidas pela propagação da luz através dos tecidos biológicos.

2. Processamento de Sinais: Na área de processamento de sinais, a deconvolução é usada para remover distorções introduzidas por sistemas de comunicação ou sensores.

3. Astronomia: Na astronomia, a deconvolução é usada para melhorar a resolução de imagens astronômicas, permitindo aos astrônomos estudar objetos celestes com mais detalhes.

4. Tomografia Computadorizada: Em técnicas de tomografia, como a tomografia por emissão de pósitrons (PET) e a tomografia computadorizada (CT), a deconvolução é usada para melhorar a qualidade das imagens reconstruídas.

Desafios e Considerações

Embora a deconvolução seja uma ferramenta poderosa, ela também apresenta desafios significativos. Um dos principais desafios é que a deconvolução é muitas vezes uma tarefa malposta, o que significa que existem múltiplas soluções possíveis ou que a solução ótima pode ser difícil de encontrar.

Além disso, a deconvolução pode ser computacionalmente intensiva, especialmente em casos onde a função de convolução é mal condicionada ou mal definida. À medida que continua o avanço na compreensão e aplicação dessa técnica, pode-se esperar ver ainda mais descobertas e inovações em uma ampla gama de disciplinas.