Problema de roteamento de veículos capacitados
Este artigo carece de caixa informativa ou a usada não é a mais adequada. |
Esta página cita fontes, mas que não cobrem todo o conteúdo. |
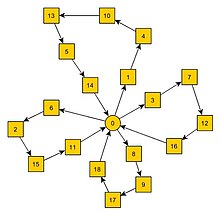
O problema de roteamento de veículos capacitados (PRVC) é a variante mais estudada do problema de roteamento de veículos, e tem alta relevância acadêmica[carece de fontes]. De forma simples, pode-se definir o problema como: Dado um conjunto de pedidos de transporte e uma frota de veículos, o problema é encontrar um plano para determinar um conjunto de rotas de veículos que realize o transporte total ou parcial desses pedidos com a frota de veículos em questão a um custo mínimo; em particular, decidir em qual veículo serão alocados os pedidos, e em que sequência, tal que todas as rotas desses veículos podem ser executadas de forma viável. Nesse tipo de problema, os pedidos de transporte a atender estão geralmente concentrados em pontos específicos de uma rede rodoviária[1].
Existe um grande número de aplicações no mundo real empregando métodos de solução baseados no PRVC com auxílio de ferramentas computacionais. O sucesso da utilização dessas técnicas de otimização não se deve apenas ao poder dos dispositivos computacionais e à plena integração com sistemas de informação e modelos de negócios, mas também pode ser atribuído ao desenvolvimento de modelos matemáticos rigorosos, que são capazes de levar em conta grande maioria das características do VRP que surgem nas aplicações do mundo real.
Além disso, os algoritmos correspondentes e as suas implementações computacionais assumem um papel essencial na busca de soluções viáveis de alta qualidade para as instâncias do mundo real, e com tempo de computação aceitáveis. Comparado aos procedimentos não baseados em otimização combinatória, o ganho de economia e redução de custos é significativo quando na utilização de frotas de veículos.
Nos últimos anos, foram desenvolvidas muitas ferramentas de software integrando serviços de transmissão eletrônica de dados entre veículos e administradores de frotas. O objetivo dessas ferramentas é permitir uma reação mais rápida dos planejadores à dinâmica do sistema de transporte e às possíveis perturbações causadas pela avaria de veículos ou pelas condições ruins de tráfego nas estradas.
Definição do problema[editar | editar código-fonte]
No PVRC, os pedidos de transporte consistem na distribuição de mercadorias provenientes de um depósito, designado como ponto 0, para um dado conjunto de n outros pontos, normalmente referidos como clientes, N = {1,2,...,n}. A quantia que tem de ser entregue ao cliente i N é a procura do cliente, que é dada por um escalar , por exemplo, o peso da mercadoria a entregar.
A frota K = {1,2,...,|K|} é presumidamente homogênea, o que significa que |K| disponíveis no depósito, todos têm a mesma capacidade Q > 0, e estão funcionando em custos idênticos. Um veículo que serve um subconjunto de clientes S N começa no depósito, desloca-se uma vez a cada um dos clientes em S, e finalmente regressa ao depósito. Um veículo em movimento de i a j incorre no custo da viagem .
Os dados do problema podem ser estruturados utilizando tanto um grafo não direcionado quanto um dígrafo. Assim, V = {0} N = {0,1,...,n} é o conjunto de vértices. O depósito é definido como := 0. Globalmente, uma instância PRVC é exclusivamente definida por um grafo completo ponderado G = (V, E, , ) ou um dígrafo G = (V, A, , ) juntamente com o tamanho |K| da frota de veículos K e da capacidade do veículo Q.
Uma rota é uma sequência r = () com = = 0, na qual o conjunto S = {} N de clientes é visitado.
O problema de roteamento de veículos capacitados tem vocabulário especifico. Os objetos chamados cidades no ambiente do TSP são referenciados como clientes no PRVC. Os vendedores são chamados veículos. O ponto de partida comum é denotado como o depósito. No PRVC tem-se um depósito, um conjunto de n clientes, um conjunto de m veículos e uma distância medida. No PRVC cada veículo tem uma capacidade Q e cada cliente i {1, . . . n} tem uma procura . A partir disso, a tarefa será construir rotas de veículos de modo a que todos os clientes são servidos exatamente uma vez e de modo a que as capacidades dos veículos sejam obedecidas. Isto deve ser feito enquanto se minimiza a distância total percorrida. O modelo matemático para o problema é definido como G = (V, A) em que G seja um grafo dirigido, V = {0, 1, . . . ., n, n + 1} seja o conjunto de nós no grafo, onde os nós 0 e n + 1 correspondem ao depósito e os nós {1, . . . . , n} correspondem aos clientes. Na definição a seguir, o depósito é dividido em dois nós para facilitar a modelagem: o nó 0 corresponde ao início das rotas e n + 1 corresponde ao fim dos percursos [2].
As distâncias são dadas como uma matriz (), com i, j {0, . . . ., n + 1}.
Uma rota r deve ser um caminho simples (nenhum nó é visitado duas vezes) do nó 0 ao nó n + 1.
O caminho pode ser escrito como (1.0)
onde , para i {0, . . . ., h + 1} são os nós visitados na rota. Temos necessariamente = 0 e = n + 1. O valor h é o número de clientes visitados na rota. O itinerário deve satisfazer a necessidade de capacidade, que pode ser escrita como
(1.1)
O custo de uma rota é dado por (1.2)
Seja R o conjunto de todas as rotas viáveis e () seja uma matriz booleana com n linhas e |R| colunas. Declara-se = 1 se e só se a rota servir o cliente i. O PRVC pode ser formulado como
(1.3)
sujeito a
(1.4)
(1.5)
(1.6)
A função objetivo (1.3) seleciona um conjunto de rotas viáveis que minimiza a soma do custo da rota enquanto a equação (1.4) assegura que todos os clientes são servidos exatamente uma vez e a equação (1.5) assegura que são utilizados exatamente m veículos. Em algumas variantes da equação PRVC (1.5) é relaxada de tal forma que no máximo sejam utilizados m veículos ou que não haja restrições quanto ao número dos veículos utilizados.
Uma variante do PRVC que é frequentemente estudada na literatura heurística é a distância limitada PRVC, onde uma medida de distância (possivelmente diferente de ) é atribuída a cada arco. Nenhuma rota deve ser mais longa do que D. Esta restrição é facilmente acrescentada ao modelo, bastando simplesmente exigir que as visitas no caminho viável , devem satisfazer
(1.7)
A restrição (1.7) também pode ser vista como um limite do tempo gasto na rota e os tempos de serviço nos clientes podem ser incorporados em ().
O PRVC foi introduzido por Dantzig e Ramser[3] e tem sido sujeito a intensa pesquisa desde então. Muitos métodos heurísticos têm sido propostos nas últimas 5 décadas. Em 1965, Clarke e Wright [4] publicaram a mais famosa solução heurística para o problema. Essa solução foi centenas de vezes melhorada, e permanece ainda muito estudada.
Por fim, o PRVC pode ser resumido em duas tarefas interdependentes: (i) a partição do conjunto N de clientes em clusters viáveis ; (ii) o encaminhamento de cada veículo k K até {0} [1] .
Extensões, modificações e adaptações[editar | editar código-fonte]
Entrega. Distribuição de mercadorias de um depósito aos clientes. Por exemplo, entrega de pacotes de produtos adquiridos em regime de pré-venda.
Coleta. Contrapartida da entrega aos clientes é a coleta a partir de clientes, em que todas as tarefas envolvem a movimentação de mercadorias ou resíduos de um ponto para o depósito. As coletas são muitas vezes chamadas pickups. Os problemas de encaminhamento associados ocorrem frequentemente ou no início de uma cadeia de abastecimento, por exemplo, para a coleta de leite de um produtor; ou logo no final, por exemplo, na logística inversa onde os vazios vasilhames são devolvidos.
Visitas simples e agendamento de veículos. As vezes, o serviço não é nem de coleta nem entrega, mas apenas uma visita ao cliente ou local. Por exemplo, os serviços técnicos para instalar ou reparar um equipamento. Ou visitas de um vendedor em operação rotineira de pré-venda.
Serviços Alternativos e Indiretos. Existem situações em que um serviço pode ser executado de formas e modos alternativos. Por exemplo, a entrega de uma encomenda pode ser realizada no local de trabalho de uma pessoa no horário de expediente, na sua residência, ou em terminal de encomendas.
Transporte Ponto-a-Ponto. Nesses casos, os pedidos de transporte consistem no movimento de mercadorias ou mesmo pessoas entre dois locais particulares , onde o objeto é coletado, para ser entregue em local correspondente previamente determinado. Geralmente, nenhum destes locais é um depósito. O veículo parte de um ponto específico, mas não formalmente um depósito, para a sua primeira entrega, e sucessivamente para os pontos que deve visitar. Estes problemas são também referenciados como sendo Pickup-and-Delivery.
Fornecimento repetido. No contexto da entrega de mercadorias, os clientes podem combinar o recebimento recorrente de mercadorias. Considerando um horizonte de planejamento mais longo, um cliente pode não ter que se preocupar com o dia específico em que recebe uma remessa, desde que a mercadoria não fique sem estoque.
Serviços Divididos e Não Divididos. Por definição, todas as tarefas da entrega são executadas por um único veículo numa única operação. Mas pode ser necessário a divisão de alguns serviços: Se a procura excede a capacidade do veículo, mais do que uma visita é inevitável. Por outro lado, o serviço pode ser desdobrado em vários pedidos de serviços menores podendo gerar redução de custos significativas.
Transporte combinado e serviço multimodal. Considerando que no serviço individual as entregas são divididas em partes menores, as remessas combinadas deixam as remessas individuais fora do planejamento. Vários veículos transportam a remessa do seu fornecedor para o cliente, pontos de transferência intermédios ou centros de consolidação. Essa é uma prática comum em transporte multimodal, onde diferentes tipos de veículos e modos de transporte são utilizados em várias etapas: por exemplo, empregam caminhões de grandes dimensões para a carga completa cobrindo longas distâncias, transferindo das fábricas para os centros de distribuição em pequenos caminhões de carga inferior para um caminhão comum/camionete até aos clientes finais.
Roteiro com lucros e seleção de serviços. Com uma frota limitada, pode ser impossível atender a todos os pedidos de transporte. Então, apenas um subconjunto de pedidos tem de ser entregue. De forma mais geral, visando otimizar o encaminhamento uma empresa pode obter receitas adicionais em comparação com as fases tradicionais decisões, em que a aceitação do pedido precede a etapa de planejamento da rota. A fim de percorrer este processo de seleção de pedidos, pode-se ou estabelecer restrições quanto aos níveis de serviços e custos, respectivamente.
Roteiro Dinâmico e Estocástico. Nesse caso, considera-se a incerteza e variações das condições do sistema. Em geral, um problema pode ser dinâmico se partes ou toda a informação relevante sobre as condições do sistema se tornarem disponíveis durante a operação; ou estocástico se as condições do sistema são incertas, mas a incerteza é descrita por uma dada distribuição de probabilidade. No caso dinâmico, a informação geralmente revelada ao longo do tempo da operação, consiste em localizações e exigências: algumas dessas exigências podem ser conhecidas com antecedência. Dois outros tipos de problemas dinâmicos são bem estudados: O primeiro considera-se a dependência temporal da duração da viagem. No segundo tipo, a disponibilidade e a capacidade dos veículos é uma componente dinâmica do problema, que requer reagendamento das rotas quando ocorrem avarias e atrasos nos veículos. No PRVC estocástico, alguns componentes problemáticos, tais como a procura do cliente e as viagens vezes, são incertas e descritas como variáveis aleatórias. Assim, as rotas planejadas podem sofrer atrasos no serviço aos clientes e podem ser encerradas prematuramente quando a capacidade do veículo foi alcançada. O foco do PRVC estocástico está, portanto, na análise do impacto da não certeza sobre os custos e níveis de serviço resultantes.
Referências[editar | editar código-fonte]
Stefan Ropke (2006). «Heuristic and exact algorithms for vehicle routing problems». Copenhagen, Denmark: University of Copenhagen (DIKU)
G. CLARKE AND J. W. WRIGHT (1964). «Scheduling of vehicles from a central depot to a number of delivery points». pp. 568–581
G. B. DANTZIG AND J. H. RAMSER), pp. 80–91. (1959). «The truck dispatching problem». pp. 80–91.
Vehicle routing : problems, methods, and applications. Toth, Paolo,, Vigo, Daniele,, Society for Industrial and Applied Mathematics, Second edition ed. Philadelphia, Pennsylvania: [s.n.] OCLC 896212133
- ↑ a b Vehicle routing : problems, methods, and applications. Toth, Paolo,, Vigo, Daniele,, Society for Industrial and Applied Mathematics, Second edition ed. Philadelphia, Pennsylvania: [s.n.] OCLC 896212133
- ↑ Pisinger, David; Ropke, Stefan (agosto de 2007). «A general heuristic for vehicle routing problems». Computers & Operations Research (8): 2403–2435. ISSN 0305-0548. doi:10.1016/j.cor.2005.09.012. Consultado em 11 de janeiro de 2021
- ↑ Dantzig, G. B.; Ramser, J. H. (outubro de 1959). «The Truck Dispatching Problem». Management Science (1): 80–91. ISSN 0025-1909. doi:10.1287/mnsc.6.1.80. Consultado em 11 de janeiro de 2021
- ↑ Clarke, G.; Wright, J. W. (agosto de 1964). «Scheduling of Vehicles from a Central Depot to a Number of Delivery Points». Operations Research (4): 568–581. ISSN 0030-364X. doi:10.1287/opre.12.4.568. Consultado em 11 de janeiro de 2021






























