Árvore de Pitágoras

A Árvore de Pitágoras é um fractal plano formado por quadrados. Leva o nome de Pitágoras porque cada trio de quadrados que se tocam inclui um ângulo reto, em uma configuração tradicionalmente usada para descrever o teorema de Pitágoras. Se o maior quadrado da estrutura tiver dimensões L×L, toda a árvore terá dimensões 6L×4L.
Construção
[editar | editar código-fonte]A construção de uma Árvore de Pitágoras começa com um quadrado. Acima desse quadrado, são postos dois outros quadrados, reduzidos por um fator linear de √2/2, de maneira que os cantos dos quadrados coincidam formando um par. O mesmo processo então é aplicado recursivamente para os dois quadrados, ad infinitum. A ilustração abaixo mostra as primeiras iterações na construção desse processo.[1][2]
 |
 |
 |
 |
| Ordem 0 | 1ª ordem | 2ª ordem | 3ª ordem |
Área
[editar | editar código-fonte]A n-ésima iteração na construção adiciona 2n quadrados de área , para uma área total de 1. Assim, a árvore aparenta crescer sem limites conforme n → ∞. Porém, alguns dos quadrados se sobrepõem a partir da iteração de 5ª ordem, e a árvore acaba tendo uma área finita pois consegue caber em uma caixa de 6×4.[1]
Pode-se facilmente mostrar que a área A da Árvore de Pitágoras tem que estar dentro do intervalo 5 < A < 18, que pode ser reduzido ainda mais com algum esforço. Pouco se sabe sobre o real valor de A.
Variando o ângulo
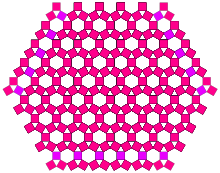
[editar | editar código-fonte]Um interessante arranjo de variações pode ser construído mantendo um triângulo isóceles mas mudando o ângulo da base (90° para a árvore padrão). Em particular, quando o meio-ângulo original é definido como (30°) = arcsen(0.5), torna-se facilmente visualizável que o tamanho dos quadrados se mantem constante. A primeira sobreposição ocorre na quarta iteração. O padrão geral é a de um ladrilho rombitriexagonal, um conjunto de hexágonos circundado pelos quadrados construídos.

|
|
| 4ª ordem | 10ª ordem |
No limite onde o meio-ângulo é 90°, obviamente não existe sobreposição, e a área total coberta é igual ao dobro da área do quadrado original. Seria interessante de saber se existe alguma relação algorítmica entre o valor do meio-ângulo base e a iteração em que a primeira sobreposição ocorre.
História
[editar | editar código-fonte]A Árvore de Pitágoras foi construída pela primeira vez por Albert E. Bosman (1891-1961), um professor de matemática Holandês.[1][3]
Veja também
[editar | editar código-fonte]Referências
[editar | editar código-fonte]- ↑ a b c Wisfaq.nl.
- ↑ Pourahmadazar, J.; Ghobadi, C.; Nourinia, J. (2011). «Novel Modified Pythagorean Tree Fractal Monopole Antennas for UWB Applications». New York: IEEE. IEEE Antennas and Wireless Propagation Letters. 10: 484–487. Bibcode:2011IAWPL..10..484P. doi:10.1109/LAWP.2011.2154354
- ↑ Arsetmathesis.nl Arquivado em 2009-01-18 no Wayback Machine
Referências externas
[editar | editar código-fonte]- Gallery of Pythagoras trees
- Interactive generator with code
- «Pythagoras tree with different geometries as well as in 3D». Arquivado do original em 15 de janeiro de 2008
- Pythagoras Tree by Enrique Zeleny based on a program by Eric W. Weisstein, The Wolfram Demonstrations Project.
- Weisstein, Eric W. «Pythagoras Tree». MathWorld (em inglês)
- Three-dimensional Pythagoras tree
- MatLab script to generate Pythagoras Tree
- Pourahmadazar, J.; Ghobadi, C.; Nourinia, J. (2011). «Novel Modified Pythagorean Tree Fractal Monopole Antennas for UWB Applications». New York: IEEE. IEEE Antennas and Wireless Propagation Letters. 10: 484–487. Bibcode:2011IAWPL..10..484P. doi:10.1109/LAWP.2011.2154354


