Computing machinery and intelligence

Computing Machinery and Intelligence, escrito por Alan Turing e publicado em 1950 na revista Mind, é um artigo pioneiro sobre inteligência artificial, sendo o primeiro trabalho a introduzir o conceito do que é hoje conhecimento como o Teste de Turing.

Neste trabalho de Turing tenta responder à questão "Máquinas podem pensar?" O autor sugere que "se troque a pergunta por outra, que está intimamente relacionada à primeira e é expressa em palavras relativamente menos ambíguas.", já que as palavras, segundo Turing, "pensar" e "máquina" não podem ser definidas de uma maneira clara que satisfaça a todos. Para fazê-lo, ele deve primeiro encontrar uma ideia simples e livre de ambiguidade que substitua a palavra "pensar", depois esclarecer precisamente quais "máquinas" ele está considerando, e, finalmente, munido dessas ferramentas, ele formula a nova pergunta, relacionada à primeira, que ele acredita poder responder afirmativamente.

Teste de Turing

A "interpretação padrão" do Teste de Turing, no qual o jogador C, o interrogador, tem a tarefa de tentar determinar qual jogador - A ou B - é um computador e qual é um humano. Imagem adaptada de

Ver artigo principal: Teste de Turing

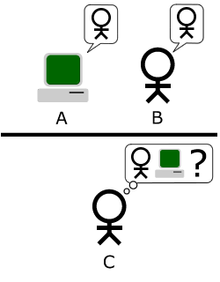
Ao invés de tentar determinar se uma máquina está ou não pensando, Turing sugere que deveríamos perguntar se a máquina pode ganhar um jogo, chamado de "Jogo da Imitação". A versão original deste jogo envolve três participantes (A, B e C) em salas isoladas: um homem (A); uma mulher (B); e um terceiro participante (C), que atua como interrogador, e que pode ser de ambos os sexos. O jogador C não pode ver os jogadores A e B, e os conhece apenas por X e Y, podendo se comunicar com eles apenas através de notas escritas ou outra forma que não sugira qualquer detalhe sobre seus gêneros. Através de perguntas, C tenta determinar os gêneros de X e Y, sabendo que há, necessariamente, um homem e uma mulher. O objetivo de A é enganar C fazendo-o acreditar que ele (A ou X) é mulher e que B (ou Y) é homem, enquanto o objetivo de B é auxiliar o interrogador a tomar a decisão certa.

Turing propõe uma variação ao "Jogo da Imitação", envolvendo o computador. Assim, os três participantes do jogo, na versão de Turing são: um computador (objeto do teste), participante A; um humano, participante B; e um juiz (humano), participante C. O juiz humano pode conversar com ambos, o humano e o computador, digitando em um terminal. Tanto o computador quanto o humano tentam convencer o juiz de que eles são o humano. Se o juiz não puder dizer consistentemente qual é qual, então o computador ganha o jogo. Será que o interrogador vai decidir erroneamente quando o jogo é jogado desta forma tanto quanto ele o faz quando o jogo é disputado entre um homem e uma mulher? Essas perguntas substituem nossa original, 'Máquinas podem pensar?'"

Como Stevan Harnad observa, a pergunta se tornou "Máquinas podem fazer o que nós (como entidades pensantes) podemos fazer?" Em outras palavras, Turing já não pergunta se uma máquina pode "pensar"; ele está perguntando se uma máquina pode agir indistintamente da maneira que um ser pensante age. Essa questão evita o difícil problema filosófico de predefinir o verbo "pensar" e em vez disso foca nas capacidades de desempenho que estar apto a pensar torna possíveis, e como um sistema causal pode gerá-las. Alguns tem interpretado a pergunta de Turing como "Pode um computador, comunicando-se através de um telétipo, enganar uma pessoa ao fazê-la acreditar que ele é humano?" mas se mostra claro que Turing não estava falando de enganar pessoas mas sobre gerar capacidade cognitiva humana.

Máquinas Digitais

Turing também notou que nós precisamos determinar que "máquinas" desejamos considerar. Ele aponta que um clone humano, artificial, não forneceria um exemplo muito interessante. Turing sugeriu que nós deveríamos focar nas aptidões de máquinas digitais que manipulam os dígitos binários 1 e 0, reescrevendo eles na memória usando regras simples. Ele deu duas razões:

• Primeiro, não há razão para especular se elas podem ou não existir. Elas já existiam em 1950.
• Segundo, máquinas digitais são "universais". A pesquisa de Turing em fundamentos da computação provou que um computador digital pode, em teoria, simular o comportamento de qualquer outra máquina digital, se houver memória e tempo suficientes. (Essa é essencialmente a visão da tese de Church-Turing e da máquina de Turing universal.) Portanto, se qualquer máquina digital pode "agir como se pensasse" então, toda máquina digital suficientemente poderosa pode. Turing escreve, "todos os computadores digitais são de certo modo equivalentes."

Isto permite que a questão original fique ainda mais específica. Turing agora reapresenta a pergunta original como "Vamos fixar nossa atenção em um computador digital em particular: C. Seria verdade que modificando esse computador para que tenha um armazenamento adequado, aumentando sua velocidade de resposta convenientemente, e providenciando-lhe um programa apropriado, C pode então jogar satisfatoriamente a parte de A no jogo da imitação, enquanto a parte de B é jogada por um humano?"

Esta pergunta, ele acredita, pode ser respondida sem recorrer à especulação ou filosofia. Essa se tornou uma questão direta da engenharia de software. Por isso, Turing declara que o foco não é "se todos os computadores digitais se sairiam bem no jogo, nem se os computadores atualmente disponíveis se sairiam bem, mas se existem computadores imagináveis que se sairiam bem". O mais importante é considerar os avanços possíveis no estado de nossas máquinas atuais, independentemente de termos o recurso disponível para criar uma ou não.

Nove objeções comuns

Tendo esclarecido a questão, Turing voltou-se a respondê-la. Ele considerou as nove objeções comuns a seguir, que incluem todos os principais argumentos contra inteligência artificial levantados desde que seu trabalho foi publicado pela primeira vez:

1. Objeção Teológica: diz que pensar é uma função da alma imortal do homem; portanto, uma máquina não pode pensar. "Na tentativa de construir tais máquinas," escreveu Turing, "nós não devemos estar usurpando irreverentemente Seu poder de criar almas, mais do que estamos na procriação dos filhos: antes somos, em qualquer caso, instrumentos da Sua vontade providenciando mansões para as almas que Ele cria."
2. Objeção 'Cabeças na Areia' : "As consequências de máquinas pensarem seriam terríveis. Vamos esperar e acreditar que elas não podem fazê-lo." Esse pensamento é popular entre pessoas intelectuais, por acreditarem que a superioridade deriva da inteligência superior e a possibilidade de ser ultrapassado é uma ameaça (como máquinas possuem capacidades de memória eficientes e velocidade de processamento, máquinas excedendo as capacidades de aprendizado e conhecimento são altamente prováveis). Essa objeção é uma falácia apelo às consequências, confundindo o que não deveria ser com o que pode ou não ser (Wardip-Fruin, 56).
3. Objeções Matemáticas: Essa objeção usa teoremas matemáticos, como o teorema da incompletude de Gödel, para mostrar que existem limites a quais questões um sistema computacional baseado em lógica pode responder. Turing sugere que humanos estão frequentemente errados e satisfeitos com a falibilidade de uma máquina. (Esse argumento seria feito novamente pelo filósofo John Lucas em 1961 e pelo físico Roger Penrose em 1989.)
4. Argumento da Consciência: Esse argumento, sugerido pelo Professor Geoffrey Jefferson em 1949, diz que "até que uma máquina possa escrever um soneto ou compor um concerto por conta de pensamentos e emoções sentidas, e não pela queda de oportunidade de símbolos, podemos concordar que máquina se iguala a cérebro." Turing replica dizendo que nós não temos como saber que outros indivíduos além de nós mesmos têm emoções, e que então deveríamos aceitar o teste. Ele adiciona, "Eu não desejo dar a impressão que eu penso que não há mistério sobre a consciência... Mas eu não acho que esses mistérios precisam necessariamente ser resolvidos antes que possamos responder a questão [se máquinas podem pensar]." (Esse argumento, que um computador não pode ter experiências de consciência ou entendimento teria sido feito em 1980 pelo filósofo John Searle em seu argumento do quarto chinês. A réplica de Turing é agora conhecida como a réplica de outras mentes".
5. Argumentos de várias deficiências. Todos esses argumentos têm a forma "um computador nunca fará X". Turing propõe uma seleção:

Seja gentil, cheio de recursos, bonito, amigável, tenha iniciativa, tenha senso de humor, diferencie o certo e o errado, cometa erros, se apaixone, aprecie morango e creme, faça alguém se apaixonar com isso, aprenda da experiência, use palavras apropriadamente, seja o sujeito do seu próprio pensamento, tenha tanta diversidade de comportamento quando um homem, faça algo realmente novo. Turing nota que "nenhum suporte é dado a essas declarações," e que elas dependem de suposições ingênuas sobre o quão versáteis máquinas podem ser no futuro, ou são "formas disfarçadas do argumento da consciência." Ele escolhe responder algumas delas:

Máquinas não podem cometer erros. Ele nota que é fácil programar uma máquina para parecer cometer um erro;

Uma máquina não pode ser o sujeito do seu próprio pensamento (ou não pode ter consciência própria). Um programa que pode informar seus estados internos e processos, como um simples programa depurador, pode certamente ser escrito. Turing afirma "uma máquina pode sem dúvidas ser seu próprio assunto."

Uma máquina não pode ter muita diversidade de comportamento. Ele nota que, com capacidade de armazenamento suficiente, um computador pode se comportar em um número astronômico de diferentes maneiras

1. Objeção da Lady Lovelace: Uma das mais famosas objeções diz que computadores não têm capacidade de originalidade. Isso se dá principalmente porque, de acordo com Ada Lovelace, máquinas não têm capacidade de aprendizado independente. A Máquina Analítica não tem quaisquer pretensões de originar algo. Ela pode fazer tudo o que nós sabemos como ordená-la a realizar. Ela pode seguir a análise; mas não tem poder de antecipar qualquer relação ou verdade analítica. Turing sugere que a objeção de Lovelace pode ser reduzida à afirmação que computadores "nunca podem nos surpreender" e argumenta que, ao contrário, computadores podem ainda surpreender humanos, em particular quando as consequências de diferentes fatos não são imediatamente reconhecíveis. Turing também argumenta que Lady Lovelace estava dificultada pelo contexto do qual ela escreveu, e se mais conhecimento científico contemporâneo fosse exposto, se tornaria evidente que a capacidade do cérebro é similar a de um computador.

2. Argumento da continuidade no sistema nervoso: Pesquisas neurológicas modernas mostraram que o cérebro não é digital. Apesar de neurônios dispararem um pulso tudo-ou-nada, tanto o tempo exato do pulso quanto a probabilidade do pulso ocorrer têm componentes análogos. Turing reconhece isso, mas argumenta que qualquer sistema análogo pode ser simulado a um grau razoável de precisão, dado poder computacional suficiente. (O filósofo Hubert Dreyfus faria esse argumento contra "a hipótese biológica" em 1972.)

3. Argumento da informalidade do comportamento: Esse argumento afirma que qualquer sistema governado por leis será previsível e portanto não verdadeiramente inteligente. Turing replica afirmando que essas são leis confusas de comportamento com regras gerais de conduta, e que se em uma escala ampla o suficiente (como é evidente no homem) o comportamento de máquina se tornaria cada vez mais difícil de prever. Ele argumenta que, só porque nós não podemos ver de imediato quais são as leis, não significa que essas leis não existem. Eles escreve "nós certamente desconhecemos circunstâncias nas quais poderíamos dizer, 'nós pesquisamos o suficiente. Não existem tais leis.'". (Hubert Dreyfus argumentaria em 1972 que o raciocínio humano e resolução de problemas não são baseados em regras formais, mas em instintos e consciência que nunca seriam capturados em regras. Pesquisas mais recentes de IA em robótica e inteligência computacional tentam encontrar as regras complexas que governam nossas habilidades "informais" e inconscientes de percepção, mobilidade e padrão de correspondência. Veja Dreyfus' critique of AI)

Percepção extrassensorial: Em 1950, percepção extrassensorial era uma área ativa de pesquisa e Turing escolhe dar a PES o benefício da dúvida, argumentando que condições poderiam ser criadas nas quais telepatia não afetaria o teste.

Aprendizado de Máquina

Turing encerra o trabalho especulando sobre o design que uma máquina que pode passar no teste poderia ter. Sua discussão enfatiza a função da aprendizagem de máquina.

Ver também

• Teste de Turing

Referências

• Brooks, Rodney (1990), «Elephants Don't Play Chess» (PDF), Robotics and Autonomous Systems, 6: 3–15, doi:10.1016/S0921-8890(05)80025-9, consultado em 30 de agosto de 2007 
• Predefinição:Crevier 1993
• Dreyfus, Hubert (1972), What Computers Can't Do, ISBN 0-06-011082-1, New York: MIT Press 
• Dreyfus, Hubert; Dreyfus, Stuart (1986), Mind over Machine: The Power of Human Intuition and Expertise in the Era of the Computer, Oxford, UK: Blackwell 
• Dreyfus, Hubert (1979), What Computers Still Can't Do, New York: MIT Press .
• Harnad, Stevan; Scherzer, Peter (2008), «First, Scale Up to the Robotic Turing Test, Then Worry About Feeling», Artificial Intelligence in Medicine, 44 (2): 83–9, PMID 18930641, doi:10.1016/j.artmed.2008.08.008 .
• Haugeland, John (1985), Artificial Intelligence: The Very Idea, Cambridge, Mass.: MIT Press .
• Moravec, Hans (1976), The Role of Raw Power in Intelligence 
• Predefinição:Russell Norvig 2003
• Searle, John (1980), «Minds, Brains and Programs», Behavioral and Brain Sciences, 3 (3): 417–457, doi:10.1017/S0140525X00005756 
• Turing, Alan (outubro de 1950), «Computing Machinery and Intelligence», Mind, LIX (236): 433–460, doi:10.1093/mind/LIX.236.433, cópia arquivada em 2 de julho de 2008 
• Saygin, A.P.Turing Test: 50 years later. Minds and Machines. 2000. Vol. 10, No. 4. pp 463–518.
• Noah Wardrip-Fruin and Nick Montfort, eds. The New Media Reader. Cambridge: MIT Press, 2003. ISBN 0-262-23227-8. "Lucasfilm's Habitat" pp. 663–677.

Ligações externas

• PDF with the full text of the paper
• Full text of the paper
• Full text of the paper
• An analysis and review of the next 50 years