Escada de Penrose
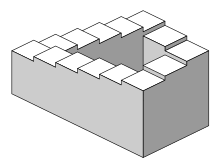
A escada de Penrose ou os degraus de Penrose, também apelidada de escada impossível, é um objeto impossível criado por Oscar Reutersvärd em 1937[1][2][3][4] e posteriormente tornado, independentemente, popular por Lionel Penrose e seu filho Roger Penrose.[5] Ela é, uma variação do triângulo de Penrose, uma representação bidimensional de uma escada em que as escadas fazem quatro curvas de 90 graus conforme sobem ou descem, mas formam um loop contínuo, de modo que uma pessoa pode escalá-las para sempre e nunca mais alto. Isso é claramente impossível na geometria euclidiana tridimensional.
A "escada contínua" foi apresentada pela primeira vez em um artigo que os Penroses escreveram em 1959, baseado no chamado "triângulo de Penrose" publicado por Roger Penrose no jornal britânico de psicologia (em 1958).[5] M.C. Escher então descobriu as escadarias de Penrose no ano seguinte e fez sua, agora famosa, litografia Klimmen en dalen (subindo e descendo) em março de 1960. Penrose e Escher foram informados sobre o trabalho um do outro naquele mesmo ano.[6] Escher aprofundou o tema em sua impressão Waterval (Cachoeira), publicada em 1961.
Em seu artigo original, os Penroses observaram que "cada parte da estrutura é aceitável, como representando um lance de degraus, mas as conexões são tais que a imagem, como um todo, é inconsistente: os degraus descem continuamente no sentido horário."[7]
História da descoberta[editar | editar código-fonte]
Os Penroses[editar | editar código-fonte]
Escher, na década de 1950, ainda não havia desenhado nenhuma figura impossível (e também não tinha conhecimento de sua existência). Roger Penrose foi apresentado ao trabalho de Escher no congresso internacional de matemáticos em Amsterdã (1954). Ele ficou "absolutamente fascinado" pelo trabalho de Escher e, em sua viagem de volta à Inglaterra, decidiu produzir algo "impossível" por conta própria. Depois de experimentar vários designs de barras sobrepostas, ele finalmente chegou ao triângulo impossível. Roger mostrou seus desenhos ao pai, que imediatamente produziu diversas variantes, inclusive o impossível lance de escadas. Eles queriam publicar suas descobertas, mas não sabiam à que campo o assunto pertencia. Como Lionel Penrose conhecia o editor do jornal britânico de psicologia e o convenceu à publicar seu pequeno manuscrito, a descoberta foi, finalmente, apresentada como um assunto psicológico. Após a publicação, em 1958, os Penroses enviaram uma cópia do artigo à Escher como prova de sua estima.[8]
Enquanto os Penroses deram crédito à Escher em seu artigo, Escher mencionou em uma carta à seu filho, em janeiro de 1960, que ele estava:
trabalhando no desenho de uma nova imagem, que apresentava um lance de escadas que só subia ou descia, dependendo de como você o enxergava. "As escadas" formam uma construção circular fechada, como uma cobra mordendo o próprio rabo. E ainda assim eles podem ser desenhados na perspectiva correta: cada degrau acima (ou abaixo) do que o anterior. [...] descobri o princípio em um artigo que me foi enviado e no qual eu mesmo fui apontado como o criador de vários objetos impossíveis. Mas eu não estava familiarizado com as etapas contínuas das quais o autor havia incluído um esboço claro, mas superficial, embora eu estivesse empregando alguns de seus outros exemplos.[9]
Escher foi cativado pelas escadas sem fim e, posteriormente (em abril de 1960), escreveu uma carta aos Penroses:
Há alguns meses, um amigo meu enviou-me uma fotocópia de seu artigo... As suas figuras 3 e 4, o "lance contínuo de degraus", eram inteiramente novas para mim. Fiquei tão emocionado com a ideia que, recentemente, ela me inspirou à produzir um novo quadro, que gostaria de enviar à vocês como um símbolo de minha estima. Caso vocês tenham publicado outros artigos sobre objetos impossíveis ou tópicos relacionados, ou se vocês souberem de algum desses artigos, eu ficaria muito grato se vocês pudessem me enviar mais detalhes.
Em uma conferência de Escher em Roma (em 1985), Roger Penrose disse que foi muito inspirado pelo trabalho de Escher quando, ele e seu pai, descobriram a estrutura tribar de Penrose (isto é, o triângulo de Penrose) e as etapas contínuas.
Oscar Reutersvärd[editar | editar código-fonte]
O projeto da escadaria foi descoberto, anteriormente, pelo artista sueco Oscar Reutersvärd, mas nem Penrose nem Escher sabiam desses projetos.[4] Inspirado por um programa de rádio sobre o método de composição de Mozart, descrito como "automatismo criativo" (ou seja, cada ideia criativa escrita inspirava uma nova ideia), Reutersvärd começou à desenhar uma série de objetos impossíveis em uma viagem de Estocolmo à Paris (em 1950) da mesma maneira ("inconsciente e automática"). Ele não percebeu que sua figura era um lance contínuo de escadas enquanto desenhava, mas o processo lhe permitiu traçar seus desenhos, cada vez mais complexos, passo a passo. Quando o subindo e descendo de M.C. Escher foi enviado à Reutersvärd (em 1961), ele ficou impressionado mas não gostou das irregularidades das escadas (2 × 15 + 2 × 9). Ao longo da década de 1960, Reutersvärd enviou várias cartas à Escher, para expressar sua admiração por seu trabalho, mas o artista holandês não respondeu.[10] Roger Penrose só descobriu o trabalho da Reutersvärd em 1984.[8]
Escadaria escheriana[editar | editar código-fonte]
A escadaria escheriana é um vídeo viral baseado na ilusão das escadas de Penrose. O vídeo, filmado no instituto de tecnologia de Rochester por Michael Lacanilao, foi editado para criar uma escada aparentemente cíclica de forma que se alguém andar em qualquer direção, acabará onde começou.[11] O vídeo afirma que a escadaria, cujo nome evoca objetos impossíveis de M.C. Escher, foi construída na década de 1960 pelo arquiteto fictício Rafael Nelson Aboganda. O vídeo foi revelado como uma farsa da internet (hoax), já que pessoas viajaram para o instituto de tecnologia de Rochester para ver a escada.[12]
Na cultura popular[editar | editar código-fonte]
As escadarias de Penrose apareceram duas vezes no filme A origem. Essa ilusão paradoxal só pode ser realizada nos mundos de sonhos do filme. No filme, o herói desce as escadarias fugindo de um guarda. No mundo real, o herói deve estar sempre na frente do vilão durante esta perseguição. No entanto, no caso das escadarias de Penrose, o herói desce outro lance de escadas para alcançar o vilão e pegá-lo desprevenido.[13]
Ver também[editar | editar código-fonte]
Notas[editar | editar código-fonte]
- ↑ «Penrose stairs» [Escadaria de Penrose]. Illusions index (em inglês). Consultado em 9 de outubro de 2020
- ↑ Torre, Matteo. «Impossible pictures: when art helps math education» [Imagens impossíveis: quando a arte ajuda a educação matemática] (PDF) (em inglês). Consultado em 9 de outubro de 2020
- ↑ «Endless staircase» [Escadaria sem fim]. Impossible world (em inglês). Consultado em 9 de outubro de 2020
- ↑ a b IllusionWorks 1997
- ↑ a b Penrose & Penrose 1958, pp. 31 à 33
- ↑ Hallyn 2000, p. 172
- ↑ Ernst 1992, p. 72
- ↑ a b Ernst 1992, pp. 71 e 72
- ↑ Ernst 1992, pp. 75, 78
- ↑ Ernst 1992, pp. 70 e 71
- ↑ Schwartz, Heidi (17 de maio de 2013). «The escherian stairwell (Penrose steps) - How it works» [A escadaria escheriana (degraus de Penrose) - Como funciona]. Facility executive - creating intelligent buildings (em inglês). Consultado em 18 de abril de 2019
- ↑ Mikkelson, David. «Fact check: escherian stairwell» [Verificação de fatos: escadaria escheriana]. snopes.com (em inglês). Consultado em 18 de abril de 2019
- ↑ Harshbarger, Eric (19 de agosto de 2010). «The never-ending stories: Inception's Penrose staircase». Wired. ISSN 1059-1028. Consultado em 5 de junho de 2020
Referências[editar | editar código-fonte]
- Deutsch, Diana (julho de 2010). «The paradox of pitch circularity» (PDF). Acoustics today (em inglês). 6 (3): 8 à 14. doi:10.1121/1.3488670. Consultado em 16 de março de 2011
- Ernst, Bruno (1992). The eye beguiled: optical illusions [O olho seduzido: ilusões de ótica] (em inglês). [S.l.]: Taschen. ISBN 3-8228-9637-3
- Hallyn, Fernand (2000). Metaphor and analogy in the sciences [Metáfora e analogia nas ciências] (em inglês). [S.l.]: Springer. ISBN 978-0-7923-6560-0. Consultado em 16 de março de 2011
- IllusionWorks (1997). «Impossible staircase» [Escada impossivel] (em inglês). Consultado em 16 de março de 2011. Arquivado do original em 13 de julho de 2013
- Penrose, L.S.; Penrose, R. (1958). «Impossible objects: a special type of visual illusion» [Objetos impossíveis: um tipo especial de ilusão visual]. Jornal britânico de psicologia. 49: 31 à 33. PMID 13536303. doi:10.1111/j.2044-8295.1958.tb00634.x

