Estrela (teoria dos grafos)
| Estrela | |
|---|---|
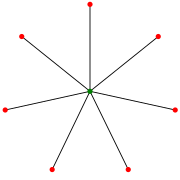 A estrela S7. | |
| vértices | k+1 |
| arestas | k |
| Diâmetro | 2 |
| Cintura | ∞ |
| Número cromático | 2 |
| Índice cromático | k |
| Propriedades | aresta-transitivo Árvore Distância-unidade Bipartido |
| Notação | Sk |
Em teoria dos grafos, uma estrela Sk é o grafo bipartido completo K1,k, uma árvore com um nó interno e k folhas. Uma estrela com 3 arestas é chamada uma garra[1].
A estrela Sk é aresta-elegante quando k é par e não quando k é ímpar. Ela é aresta-transitiva, unidade-distância e têm diâmtero 2, cintura ∞, índice cromático k e número cromático 2.
Estrelas também podem ser descritas como os únicos grafos conectados em que no máximo um vértice tem grau maior que um.
Relação com outras famílias de grafos[editar | editar código-fonte]
Garras são notáveis na definição de grafos sem garra, os grafos que não tem qualquer garra como subgrafo induzido[2][3].
Uma estrela é um tipo especial de árvore. Como acontece com qualquer árvore, as estrelas podem ser codificados por uma sequência Prüfer; A sequência Prüfer para uma estrela K1,k consiste de k − 1 cópias do vértice central[4]. Uma árvore pode ser vista como um conjunto de estrelas (pares ou ímpares) ligadas pelos pontos centrais[5].
Diversos grafos invariantes são definidos em termos de estrelas. Arboricidade de estrela é o menor número de florestas que um grafo pode ser particionado em tal modo que cada árvore em cada floresta é uma estrela[6], e o número cromático de estrela de um grafo é o menor número de cores necessário para colorir seus vértices de tal forma que cada duas classes de coloração, juntas, formam um subgrafo em que todos os componentes conectados são estrelas[7]. Os grafos de comprimento de ramo 1 são exatamente os grafos em que cada componente conectado é uma estrela[8].
Outras aplicações[editar | editar código-fonte]
O conjunto de distâncias entre os vértices de uma garra fornece um exemplo de um espaço métrico finito, que não pode ser incorporado isometricamente em um espaço euclideano de qualquer dimensão[9].
A rede em estrela, uma rede de computadores modelado em um grafo de estrela, é importante em computação distribuída.
Referências
- ↑ BOAVENTURA NETTO, Paulo Oswaldo (2001). Grafos. Teoria, Modelos Algoritmos. São Paulo: Edgard Blücher. p. 27. ISBN 85-212-0292-X
- ↑ FAUDREE, Ralph; FLANDRIN, Evelyne; RYJÁčEK, Zdeněk (1997). «Claw-free graphs — A survey». Discrete Mathematics. 164 (1–3). pp. 87–147. doi:10.1016/S0012-365X(96)00045-3.
- ↑
Chudnovsky, Maria; Seymour, Paul (2005), «The structure of claw-free graphs», Surveys in combinatorics 2005 (PDF), London Math. Soc. Lecture Note Ser., 327, Cambridge: Cambridge Univ. Press, pp. 153–171, consultado em 25 de outubro de 2010, cópia arquivada (PDF) em
|arquivourl=requer|arquivodata=(ajuda) 🔗. - ↑
Gottlieb, J.; Julstrom, B. A.; Rothlauf, F.; Raidl, G. R. (2001), «Prüfer numbers: A poor representation of spanning trees for evolutionary search», Proc. Genetic and Evolutionary Computation Conference (PDF), Morgan Kaufmann, pp. 343–350, consultado em 25 de outubro de 2010, cópia arquivada (PDF) em
|arquivourl=requer|arquivodata=(ajuda) 🔗 - ↑ BARBOSA, Ruy Madsen (1975). Combinatória e Grafos. 2. São Paulo: Livraria Nobel. p. 196
- ↑ Hakimi, S. L.; Mitchem, J.; Schmeichel, E. E. (1996), «Star arboricity of graphs», Discrete Math., 149: 93–98, doi:10.1016/0012-365X(94)00313-8
- ↑ FERTIN, Guillaume; RASPAUD, André; REED, Bruce (2004). «Star coloring of graphs». Journal of Graph Theory. 47 (3). pp. 163–182. doi:10.1002/jgt.20029
- ↑ ROBERTSON, Neil; SEYMOUR, Paul D. (1991). «Graph minors. X. Obstructions to tree-decomposition». Journal of Combinatorial Theory. 52 (2). pp. 153–190. doi:10.1016/0095-8956(91)90061-N
- ↑ Linial, Nathan (2002), «Finite metric spaces–combinatorics, geometry and algorithms», Proc. International Congress of Mathematicians, Beijing, 3, pp. 573–586, Arxiv
