Histerese
A histerese é a tendência de um sistema de conservar suas propriedades na ausência de um estímulo que as gerou, ou ainda, é a capacidade de preservar uma deformação efetuada por um estímulo. Podem-se encontrar diferentes manifestações desse fenômeno. A histerese mais conhecida ocorre no magnetismo[1], mas também pode ocorrer em diversas áreas como mecânica clássica[2], tráfego[3], biologia[4], epidemiologia[5] entre outras[6][7]. A palavra "histerese" deriva do grego antigo υστέρησις, que significa 'retardo', que foi cunhada por James Alfred Ewing em 1890.
Saturação magnética[editar | editar código-fonte]
Quando um campo magnético (ampere-espira por metro) é aplicado a um material ferromagnético, passa a circular neste uma densidade de fluxo magnética (ou indução magnética) (tesla = weber por metro quadrado). A relação entre densidade de fluxo e campo magnético é dada pela expressão [8].
Para uma geometria fixa, como o caso de uma bobina com núcleo fixo ou transformador, uma variação do campo magnético é dada por uma variação na corrente da bobina que está sendo alimentada. Quanto maior a corrente , maior o campo magnético [9].
Na região magnética linear com constante (e da ordem de ou mais), contudo, à medida que o campo magnético cresce, o material entra em uma região não linear (saturação magnética), onde passa a diminuir à medida que a saturação cresce.
Inconveniente da saturação[editar | editar código-fonte]
Quando atingida a saturação o transformador, mesmo a vazio, passa a demandar correntes maiores para manter o fluxo magnético imposto pela tensão. A relação entre fluxo magnético e tensão induzida é dada pela Lei de Faraday[10]. Uma das formas de expressá-la é por , onde é o fluxo magnético, é o tempo , o número de espiras e é a tensão induzida. Para simplificar a análise (e sem prejuízo de conceitos) consideraremos a tensão induzida no primário igual a tensão aplicada pela fonte.
Imaginando uma tensão de entrada sinusoidal , o fluxo demandado pelo núcleo do transformador será dado por , ou seja, o fluxo é diretamente proporcional a tensão e a frequência de entrada. Trabalhando mais um pouco, pode-se chegar a expressão que o fluxo de pico de um sinal sinusoidal é dado por , onde é a frequência em hertz.
A densidade de fluxo que atenda ao fluxo demandado é dada pela relação , onde é a área da secção transversal à passagem do fluxo magnético[10]. Associada a densidade de fluxo magnético está o campo magnético que o gera, dado por . Perceba que com a redução da permeabilidade (na saturação), um maior campo magnético muito maior é demandado, e este, por fim, está associado à corrente elétrica que o gera, que por consequência, pode aumentar para valores muito acima dos nominais, mesmo com o transformador a vazio.
Para evitar este inconveniente deve-se trabalhar com valores baixos de saturação, limitando a tensão aplicada, aumentando a área de ferro ou aumentando a qualidade dos materiais.
Histerese magnética[editar | editar código-fonte]

- Aumenta-se a densidade de fluxo magnética (ou indução magnética) aplicada a um material ferromagnético até a saturação. A relação entre campo e densidade de fluxo neste intervalo é dada por . Quando mais saturado o material menor o valor da permeabilidade .
- Diminuí-se a densidade de fluxo e como consequência também o campo diminui. Contudo, quando chega a zero (corrente zero), ainda existe uma densidade de fluxo remanescente, (o material fica imantado).
- Para que chegue a zero, é necessário aplicar um campo negativo, chamado de força coercitiva, .
- Se continuar aumentando no sentido negativo, o material é magnetizado com polaridade oposta. Desse modo, a magnetização inicialmente será fácil, até quando se aproxima da saturação, passando a ser difícil.
- A redução do módulo do campo novamente a zero deixa uma densidade de fluxo remanescente, , e, para reduzir a zero, deve-se aplicar uma força coercitiva no sentido positivo.
- Aumentando-se mais ainda o campo, o material fica novamente saturado, com a polaridade inicial.
Nesse fenômeno, observa-se o atraso entre densidade de fluxo e campo magnético ( quando ), chamado de histerese magnética.
O ciclo traçado pela curva de magnetização é chamado de ciclo de histerese.

B = Campo magnético [T] ou [Wb/m²]
H = Intensidade de campo magnético [A/m] ou [A.e/m]
BR = Remanescência
HC = Coercividade
Exemplo de histerese com metais[editar | editar código-fonte]
Quando o ferro não está magnetizado, seus domínios magnéticos estão dispostos de maneira desordenada e aleatória. Porém, ao aplicar uma força magnetizante, os domínios se alinham com o campo aplicado. Se invertemos o sentido do campo, os domínios também inverterão sua orientação. Num transformador, o campo magnético muda de sentido muitas vezes por segundo, de acordo com o sinal alternado aplicado. E o mesmo ocorre com os domínios do material do núcleo. Ao inverter sua orientação, os domínios precisam superar o atrito e a inércia. Ao fazer isso, dissipam uma certa quantidade de potência na forma de calor, que é chamada de perda por histerese.
Em determinados materiais, a perda por histerese é muito grande. O ferro doce é um exemplo. Já no aço, esse tipo de perda é menor. Por isso, alguns transformadores de grande potência utilizam um tipo de liga especial de ferro-silício, que apresenta uma perda por histerese reduzida. Esse tipo de problema também aumenta junto com a frequência do sinal. Um transformador que apresenta baixa perda nas frequências menores, pode ter uma grande perda por histerese ao ser usado com sinais de frequências mais altas.
A histerese produz-se devido ao gasto de energia para inverter os dipolos durante uma mudança de campo magnético.
Eletrônica[editar | editar código-fonte]
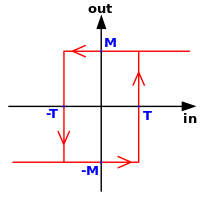
Histerese pode ser utilizada para filtrar sinais de forma que a saída reaja de maneira retardada à história desse sinal. Por exemplo, um termostato controlando um aquecedor pode acioná-lo quando a temperatura cai abaixo da temperatura de 'A' graus Celsius, mas só desligará quando a temperatura ultrapassar 'B' graus Celsius.
Um Disparador Schmitt é um circuito eletrônico simples que também exibe essa propriedade. Geralmente, uma quantidade de histerese é intencionalmente adicionada ao circuito eletrônico (ou algoritmo digital) para prevenir chaveamentos (troca de estados) rápidos.
Referências
- ↑ Bertotti, Giorgio (21 de maio de 1998). Hysteresis in Magnetism: For Physicists, Materials Scientists, and Engineers (em inglês). [S.l.]: Academic Press. ISBN 9780080534374
- ↑ Almeida, M.P.; Costa, U.M.S. (março de 2000). «Exemplo de Histerese com um Sistema de Massa-Mola» (PDF). Revista Brasileira de Ensino de Física. 22 (1): 49-53. Consultado em 26 de junho de 2018
- ↑ Hu, Mao-Bin; Wen-Xu (2 de março de 2007). «Phase transition and hysteresis in scale-free network traffic». Physical Review E (em inglês). 75 (3). 036102 páginas. doi:10.1103/PhysRevE.75.036102
- ↑ Noori, Hamid Reza. Hysteresis Phenomena in Biology - Springer. [S.l.: s.n.] doi:10.1007/978-3-642-38218-5
- ↑ Chen, Li; Fakhteh (30 de março de 2016). «Phase transitions and hysteresis of cooperative contagion processes». arXiv:1603.09082 [cond-mat, physics:physics, q-bio]
- ↑ Chakrabarti, Bikas K.; Muktish (1 de abril de 1999). «Dynamic transitions and hysteresis». Reviews of Modern Physics. 71 (3): 847–859. doi:10.1103/RevModPhys.71.847
- ↑ Piquette, Jean C.; Elizabeth A. (1 de junho de 2002). «Generalization of a model of hysteresis for dynamical systems». The Journal of the Acoustical Society of America. 111 (6): 2671–2674. ISSN 0001-4966. PMID 12083200
- ↑ Sadiku, Matthew N. O. (2004). Elementos de eletromagnetismo 3 ed. Porto Alegre: Bookman. ISBN 9788536302751. OCLC 124029850
- ↑ Assumpção., Bastos, João Pedro (2008). Eletromagnetismo para engenharia : estática e quase-estática. Florianópolis: Ed. UFSC. ISBN 9788532804181. OCLC 817147229
- ↑ a b Bastos, João Pedro Assumpção (2008). Eletromagnetismo para engenharia: estática e quase-estática. Florianópolis: Ed. UFSC. ISBN 9788532804181

























