Origem: Wikipédia, a enciclopédia livre.
A fórmula tradicional de cálculo da área do triângulo , ensinada e muito utilizada no ensino fundamental é
A
=
(
base
⋅
altura
2
)
.
{\displaystyle A=\left({\frac {{\text{base}}\cdot {\text{altura}}}{2}}\right).}
fórmula de Herão (ou de Heron), que dá a área do triângulo em função da medida dos três lados do triângulo. O nome faz referência ao matemático grego Herão de Alexandria .
A fórmula é:
A
=
p
(
p
−
a
)
(
p
−
b
)
(
p
−
c
)
,
{\displaystyle A={\sqrt {p(p-a)(p-b)(p-c)}},}
p
{\displaystyle p}
semiperímetro do triângulo e
a
,
{\displaystyle a,}
b
,
{\displaystyle b,}
c
{\displaystyle c}
comprimentos dos 3 lados do triângulo.
Um triângulo cujos lados medem 3, 25 e 26, respectivamente, tem semiperímetro (3 + 25 + 26)/2 = 27. Assim, a sua área é
A
=
27
⋅
24
⋅
2
⋅
1
=
36.
{\displaystyle A={\sqrt {27\cdot 24\cdot 2\cdot 1}}=36.}
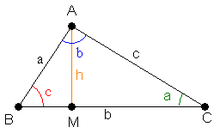
Seja
b
{\displaystyle b}
h
{\displaystyle h}
A
=
b
h
2
.
{\displaystyle A={\frac {bh}{2}}.}
Pela Lei dos cossenos ,
c
2
=
a
2
+
b
2
−
2
a
b
cos
C
=
a
2
+
b
2
−
2
b
a
2
−
h
2
,
{\displaystyle c^{2}=a^{2}+b^{2}-2ab\cos C=a^{2}+b^{2}-2b{\sqrt {a^{2}-h^{2}}},}
h
2
=
a
2
−
(
a
2
+
b
2
−
c
2
2
b
)
2
.
{\displaystyle h^{2}=a^{2}-\left({\frac {a^{2}+b^{2}-c^{2}}{2b}}\right)^{2}.}
A
2
=
b
2
h
2
4
=
b
2
(
a
2
−
(
a
2
+
b
2
−
c
2
2
b
)
2
)
4
=
(
2
a
b
)
2
−
(
a
2
+
b
2
−
c
2
)
2
16
=
(
2
a
b
−
(
a
2
+
b
2
−
c
2
)
)
(
2
a
b
+
(
a
2
+
b
2
−
c
2
)
)
16
=
=
(
c
2
−
(
a
−
b
)
2
)
(
(
a
+
b
)
2
−
c
2
)
16
=
(
c
−
a
+
b
)
(
c
+
a
−
b
)
(
a
+
b
−
c
)
(
a
+
b
+
c
)
16
=
(
s
−
a
)
(
s
−
b
)
(
s
−
c
)
s
{\displaystyle {\begin{matrix}A^{2}&=&{\frac {b^{2}h^{2}}{4}}={\frac {b^{2}\left(a^{2}-\left({\frac {a^{2}+b^{2}-c^{2}}{2b}}\right)^{2}\right)}{4}}={\frac {(2ab)^{2}-(a^{2}+b^{2}-c^{2})^{2}}{16}}={\frac {(2ab-(a^{2}+b^{2}-c^{2}))(2ab+(a^{2}+b^{2}-c^{2}))}{16}}=\\\\&=&{\frac {(c^{2}-(a-b)^{2})((a+b)^{2}-c^{2})}{16}}={\frac {(c-a+b)(c+a-b)(a+b-c)(a+b+c)}{16}}=(s-a)(s-b)(s-c)s\\\end{matrix}}}