Cobertura de arestas (teoria dos grafos)
Em teoria dos grafos, uma cobertura de arestas de um grafo é um conjunto de arestas tal que todo vértice do grafo é incidente a pelo menos uma aresta do conjunto[1]. Em ciência da computação, o problema da cobertura mínima de arestas é o problema de se encontrar uma cobertura de arestas de tamanho mínimo. É um problema de otimização que pertence a classe de problemas de cobertura e pode ser resolvido em tempo polinomial.
Definição[editar | editar código-fonte]
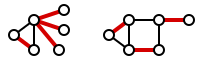
Formalmente, uma cobertura de arestas de um grafo G é um conjunto de arestas C de tal forma que cada vértice é incidente a pelo menos uma aresta em C. O conjunto C é dito cobrir os vértices de G. A figura a seguir mostra exemplos de coberturas de arestas em dois grafos.
Uma cobertura mínima de arestas é uma cobertura de arestas de menor tamanho possível. O número de cobertura de arestas é o tamanho de uma cobertura mínima de arestas. A figura a seguir mostra exemplos de coberturas de arestas mínimas.
Note que a figura à direita não é apenas uma cobertura de arestas, mas também um acoplamento. Em particular, é um acoplamento perfeito: um acoplamento M, em que cada vértice é incidente a exatamente uma aresta em M. Um acoplamento perfeito é sempre uma cobertura de arestas mínima.
Exemplos[editar | editar código-fonte]
- O conjunto de todas as arestas é uma cobertura de arestas, assumindo que não há nenhum vértice de grau-0.
- O grafo bipartido completo Km,n tem número de cobertura de arestas max(m, n).
Algoritmos[editar | editar código-fonte]
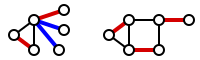
Uma cobertura mínima de arestas pode ser encontrada em tempo polinomial encontrando-se um acoplamento máximo e estendendo-a gulosamente, de modo que todos os vértices sejam cobertos. Na figura a seguir, um acoplamento máximo é marcado com vermelho; as arestas extras que foram adicionadas para cobrir nós não-acoplados são marcadas com azul. (A figura da direita mostra um grafo em que um acoplamento máximo é um acoplamento perfeito; daí que já cobre todos os vértices e nenhuma aresta extra é necessária.)
Por outro lado, o problema relacionado de encontrar uma menor cobertura de vértices e´um problema NP-difícil[2][Nota 1].
Ver também[editar | editar código-fonte]
- Cobertura de vértices
- Cobertura de conjuntos – o problema da cobertura de arestas é um caso especial do problema de cobertura de conjuntos: os elementos do universo são vértices, e cada subconjunto abrange exatamente dois elementos.
Notas[editar | editar código-fonte]
- ↑ vasco
Referências
- ↑ BOAVENTURA NETTO, Paulo Oswaldo (2001). Grafos. Teoria, Modelos Algoritmos. São Paulo: Edgard Blücher. p. 185. ISBN 85-212-0292-X
- ↑ GAREY, Michael R.; JOHNSON, David S. (1979). Computers and Intractability: A Guide to the Theory of NP-Completeness. [S.l.]: W.H. Freeman. ISBN 0-7167-1045-5