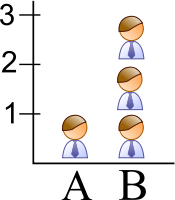Gráfico enganoso
Em estatística, um gráfico enganoso, também chamado de gráfico distorcido, é um gráfico que deturpa os dados, constituindo um uso indevido da estatística e que pode levar a conclusões incorretas.
Gráficos podem ser enganosos por serem excessivamente complexos ou mal construídos. Mesmo quando construídos para exibir as características de seus dados com precisão, os gráficos podem estar sujeitos a diferentes interpretações.[1]
Gráficos enganosos podem ser criados intencionalmente para impedir a interpretação adequada dos dados ou acidentalmente devido à falta de familiaridade com o software gráfico, má interpretação dos dados ou porque os dados não podem ser transmitidos com precisão. Gráficos enganosos são frequentemente usados em propaganda enganosa. Um dos primeiros autores a escrever sobre gráficos enganosos foi Darrell Huff, em seu livro Como Mentir com Estatística, de 1954.
O campo de visualização de dados descreve formas de apresentar informações que evitam a criação de gráficos enganosos.
Métodos
[editar | editar código-fonte][Um gráfico enganoso] É vastamente mais eficiente, não contém adjetivos, advérbios ou palavras que prejudiquem a ilusão de sóbria objetividade. Nada há que possam acusar você.
– Darrell Huff
Como Mentir com Estatítica (1954)
Existem inúmeras maneiras pelas quais um gráfico enganoso pode ser construído.[2]
Uso excessivo
[editar | editar código-fonte]O uso de gráficos onde eles não são necessários pode levar a confusão desnecessária ou interpretação errada.[3] Geralmente, quanto mais explicação um gráfico requer, menos o gráfico em si é necessário.[3] Gráficos nem sempre transmitem informações melhor do que tabelas.[4]
Rotulagem tendenciosa
[editar | editar código-fonte]O uso de palavras tendenciosas no título do gráfico, nos rótulos dos eixos ou na legenda pode influenciar inadequadamente o leitor.[3][5]
Tendências fabricadas
[editar | editar código-fonte]Da mesma forma, tentar traçar linhas de tendência entre dados não correlacionados pode induzir o leitor a acreditar que existe uma tendência onde não existe. Isso pode ser tanto o resultado de uma tentativa intencional de enganar o leitor ou devido ao fenômeno da correlação ilusória.
Gráfico de setor
[editar | editar código-fonte]- Comparar gráficos de setor de tamanhos diferentes pode ser enganoso, pois as pessoas não podem ler com precisão a área comparativa dos círculos.[6]
- O uso de setores finos, difíceis de discernir, pode ser difícil de interpretar.[6]
- O uso de porcentagens como rótulos em um gráfico de setor pode ser enganoso quando o tamanho da amostra é pequeno.[7]
- Fazer um gráfico de setor 3D ou adicionar inclinação dificultará a interpretação devido ao efeito distorcido da perspectiva.[8]
Gráfico de setor 3D em perspectiva
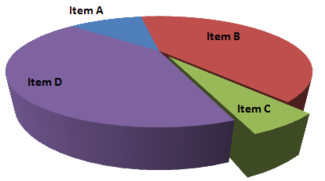
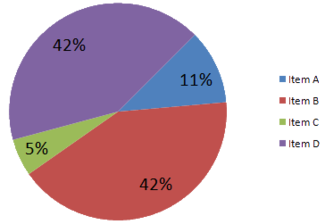
[editar | editar código-fonte]Um gráfico de setor em perspectiva (3D) é usado para dar ao gráfico uma aparência 3D. Frequentemente utilizada por motivos estéticos, a terceira dimensão não melhora a leitura dos dados; pelo contrário, eles se tornam mais difíceis de interpretar por causa do efeito distorcido da perspectiva associado à terceira dimensão. O uso de dimensões supérfluas não úteis para exibir os dados de interesse é desencorajado para gráficos em geral, não apenas para gráficos de setor.[9] Em um gráfico de setor 3D, as fatias mais próximas do leitor parecem ser maiores do que as da parte de trás devido ao ângulo em que são apresentadas.[10] Esse efeito torna os leitores menos eficientes ao julgar a magnitude relativa de cada fatia ao usar 3D do que 2D.[11]
Comparação de gráficos de setor Gráfico enganoso Gráfico comum 
O item C parece ser tão grande quanto o item A no gráfico enganoso, ao passo que, na realidade, é menos da metade do tamanho. O item D parece muito maior que o item B, mas são do mesmo tamanho.
Escala inadequada
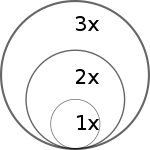
[editar | editar código-fonte]Pictogramas em gráficos de barras não devem ser dimensionados uniformemente, pois isso cria uma comparação perceptivelmente enganosa.[12] A área do pictograma é interpretada em vez de apenas sua altura ou largura.[13] Esse tipo de dimensionamento faz a diferença entre os valores parecer exponencial (quadrada).[13]
Improper scaling of 2D pictogram in a bar graph Escala inadequada Escala comum Comparação 
No gráfico em que o pictograma está dimensionado incorretamente, a imagem de B é na verdade 9 vezes maior que A.
Comparação de escala de formas 2D Quadrado Círculo Triângulo 
O tamanho percebido aumenta com a escala.
O efeito de dimensionamento impróprio de pictogramas é exemplificado ainda mais quando o pictograma tem 3 dimensões, caso em que a diferença entre os valores é representada ao cubo.[14]
O gráfico de vendas de casas (à esquerda) é enganoso. Parece que as vendas de casas cresceram oito vezes em 2001 em relação ao ano anterior, enquanto na verdade cresceram duas vezes. Além disso, o número de vendas não é especificado.
Um pictograma dimensionado incorretamente também pode sugerir que o próprio item mudou de tamanho.[15]
Enganoso Comum 
Assumindo que as figuras representam quantidades equivalentes, o gráfico enganoso implica que há mais bananas porque as bananas ocupam a maior área e estão mais à direita.
Escala logarítmica
[editar | editar código-fonte]As escalas logarítmicas são um meio válido de representar dados. Mas quando usados sem serem claramente rotulados ou exibidos para um leitor não familiarizado com eles, eles podem ser enganosos. Escalas logarítmicas são comumente usadas, por exemplo, para o índice de explosividade vulcânica, a escala Richter para terremotos, a magnitude das estrelas e o pH de soluções ácidas e alcalinas. Mesmo nesses casos, a escala logarítmica pode tornar os dados menos aparentes. Muitas vezes, a razão para o uso de escalas logarítmicas é que o autor do gráfico deseja exibir escalas muito diferentes no mesmo eixo. Sem escalas logarítmicas, comparar quantidades como 103 e 109 torna-se visualmente impraticável.[16]
Comparação de escalas lineares e logarítmicas para dados idênticos Escala linear Escala logarítmica 
.png)
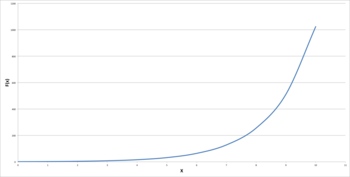
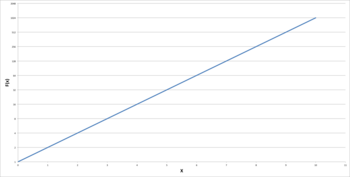
Ambos os gráficos mostram uma função exponencial idêntica de f(x) = 2x. O gráfico à esquerda usa uma escala linear, mostrando claramente uma tendência exponencial. O gráfico à direita, porém, usa uma escala logarítmica, que gera uma linha reta. Se o visualizador do gráfico não estivesse ciente disso, o gráfico pareceria mostrar uma tendência linear.
Referências
[editar | editar código-fonte]- ↑ Kirk, p. 52
- ↑ Nolan, pp. 49–52
- ↑ a b c «Methodology Manual: Data Analysis: Displaying Data - Deception with Graphs» (PDF). Texas State Auditor's Office. 4 de janeiro de 1996. Arquivado do original em 2 de abril de 2003
- ↑ Tufte, Edward R. (2006). The visual display of quantitative information 4th print, 2nd ed. Cheshire, Conn.: Graphics Press. p. 178. ISBN 9780961392147
- ↑ Keller, p. 84
- ↑ a b Whitbread, p. 150
- ↑ Soderstrom, Irina R. (2008), Introductory Criminal Justice Statistics, ISBN 9781478610342, Waveland Press, p. 17.
- ↑ Whitbread, p. 151
- ↑ Few, Stephen (agosto de 2007). «Save the Pies for Dessert» (PDF). Visual Business Intelligence Newsletter. Perceptual Edge. Consultado em 28 de junho de 2012
- ↑ Rumsey, p. 156.
- ↑ Siegrist, Michael (1996). «The use or misuse of three-dimensional graphs to represent lower-dimensional data». Behaviour & Information Technology. 15 (2): 96–100. doi:10.1080/014492996120300
- ↑ Weiss, p. 60.
- ↑ a b Utts, pp. 146–147.
- ↑ Hurley, pp. 565–566.
- ↑ Huff, p. 72.
- ↑ «Akin's Laws of Spacecraft Design». spacecraft.ssl.umd.edu. Consultado em 14 de março de 2021
Books
[editar | editar código-fonte]- Huff, Darrell (1954). How to lie with statistics. pictures by Irving Geis 1st ed. New York: Norton. ISBN 0393052648
- Hurley, Patrick J. (2000). A Concise Introduction to Logic. [S.l.]: Wadsworth Publishing. ISBN 9780534520069. (pede registo (ajuda))
- Keller, Gerald (2011). Statistics for Management and Economics abbreviated, 9th ed. Mason, OH: South-Western. ISBN 978-1111527327
- Kirk, Roger E. (2007). Statistics: An Introduction. [S.l.]: Cengage Learning. ISBN 978-0-534-56478-0. Consultado em 28 de junho de 2012
- Nolan, Susan; Heinzen, Thomas (2011). Statistics for the Behavioral Sciences. [S.l.]: Macmillan. ISBN 978-1-4292-3265-4. Consultado em 28 de junho de 2012
- Rumsey, Deborah (2010). Statistics Essentials For Dummies. [S.l.]: John Wiley & Sons. ISBN 978-0-470-61839-4. Consultado em 28 de junho de 2012
- Weiss, Neil A. (1993). Elementary statistics. [S.l.]: Addison-Wesley. ISBN 978-0-201-56640-6. Consultado em 28 de junho de 2012
- Tufte, Edward (1997). Visual Explanations: Images and Quantities, Evidence and Narrative. Cheshire, CT: Graphics Press. ISBN 978-0961392123
- Utts, Jessica M. (2005). Seeing through statistics 3rd ed. Belmont: Thomson, Brooks/Cole. ISBN 9780534394028
- Wainer, Howard (2000). Visual Revelations: Graphical Tales of Fate and Deception From Napoleon Bonaparte To Ross Perot. [S.l.]: Psychology Press. ISBN 978-0-8058-3878-7. Consultado em 19 de julho de 2012
- Whitbread, David (2001). The design manual 2nd ed. Sydney: University of New South Wales Press. ISBN 0868406589