Esfera

Uma esfera.

 Nota: Para outros significados, veja Esfera (desambiguação).

A esfera pode ser definida como "um sólido geométrico formado por uma superfície curva contínua cujos pontos estão eqüidistantes de um outro fixo e interior chamado centro"; ou seja, é uma superfície fechada de tal forma que todos os pontos dela estão à mesma distância de seu centro, ou ainda, de qualquer ponto de vista de sua superfície, a distância ao centro é a mesma.

Uma esfera é um objeto tridimensional perfeitamente simétrico. Na matemática, o termo se refere à superfície de uma bola. Na física, esfera é um objeto (usado muitas vezes por causa de sua simplicidade) capaz de colidir ou chocar-se com outros objetos que ocupam espaço.

Quanto a geometria analítica, uma esfera é representada (em coordenadas retangulares) pela equação: $(x-a)^{2}+(y-b)^{2}+(z-c)^{2}=r^{2}$ em que a, b, c são os deslocamentos nos eixos x, y, z respectivamente, e r é o raio da esfera.

e ai galerinha uma esfera é uma safada

Calota x segmento esférico

Parte azul: calota; parte branca: segmento esférico.

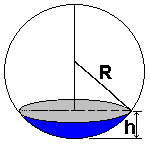
Calota seria metaforicamente "a tampa de uma laranja", demonstrada pela parte azul no desenho.

Área da calota:

$Ac=2\pi \cdot r\cdot h$

Área do Segmento Esférico:

$As=At-Ac$

Em que, As é a área do segmento, At área total da esfera e, Ac área da calota.

O volume do segmento é:

$V={\pi \cdot h^{2} \over 3}\cdot (3\cdot R-h)$

Fuso x cunha

Em azul é o fuso, em cinza é a cunha.

Fuso é uma parte da esfera, podendo ser representada por "goma de mexirica" (metaforicamente).

Área do fuso:

$Af={\alpha \over 360}\cdot 4\pi \cdot r^{2}$

$\alpha$ é o ângulo do fuso.

O volume do fuso é:

$Vc={\alpha \over 360}\cdot {4 \over 3}\cdot \pi r^{3}$

Nota-se que a área e o volume da cunha podem ambos ser obtidos subtraindo-se os respectivos valores para o fuso do valor total para a esfera.

Volume

O volume de uma semi-esfera é igual a soma dos volumes de discos, concêntricos e de espessura infinitesimal, empilhados ao longo do eixo x, de x = r (y = 0) até x = 0 onde o disco tem raio r (y = r).

Num dado x, o volume incremental (δV) é dado pelo produto da área transversal no ponto x pela largura (δx):

$\!\delta V\approx \pi y^{2}\cdot \delta x.$

O volume da semi-esfera é o somatório de todos os volumes dos discos infinitesimais.

$\!V_{\frac {1}{2}}\approx \sum \pi y^{2}\cdot \delta x.$

No limite em que δx se aproxima de zero fica:

$\!V_{\frac {1}{2}}=\int _{x=0}^{x=r}\pi y^{2}dx.$

Num dado x, um triângulo retângulo conecta x, y e r à origem, e pelo teorema de Pitágoras:

$\!r^{2}=x^{2}+y^{2}.$

Substituindo y:

$\!V_{\frac {1}{2}}=\int _{x=0}^{x=r}\pi (r^{2}-x^{2})dx.$

Calculando o integral:

$\!V_{\frac {1}{2}}=\pi \left[r^{2}x-{\frac {x^{3}}{3}}\right]_{x=0}^{x=r}=\pi \left(r^{3}-{\frac {r^{3}}{3}}\right)={\frac {2}{3}}\pi r^{3}.$

Que é o valor da semi-esfera. Dobrando este valor temos o volume total da esfera:

$\!V={\frac {4}{3}}\pi r^{3}.$

Área

Uma vez provado o volume, podemos demostrar a área da superfice a partir deste resultado (que se explica ao entender que uma esfera é a composição de "cascas de esfera" de espessura infinitesimal, "uma dentro da outra"):

${\frac {4}{3}}\pi r^{3}=\int _{0}^{r}A(r)dr.$

Derivando os dois lados da equação em relação a r:

$\!4\pi r^{2}=A(r).$

Que pode ser abreviada como:

$\!A=4\pi r^{2}.$

A área também pode ser obtida usando coordenadas esféricas. Um elemento de área da esfera, em coordenadas esféricas é dado por:

$dA=r^{2}\sin \theta \,d\phi \,d\theta .$

Portanto a área total será:

$A=\int _{0}^{2\pi }\int _{0}^{\pi }r^{2}\sin \theta \,d\phi \,d\theta =4\pi r^{2}.$

Equação da esfera em R³

Em geometria analítica, uma esfera com centro (x₀, y₀, z₀) e raio r é o lugar geométrico tal que:

$\,(x-x_{0})^{2}+(y-y_{0})^{2}+(z-z_{0})^{2}=r^{2}.$

Na forma parametrizada

$\,x=x_{0}+r\sin \theta \;\cos \varphi$

$\,y=y_{0}+r\sin \theta \;\sin \varphi \qquad (0\leq \varphi \leq 2\pi {\mbox{ e }}0\leq \theta \leq \pi )\,$

$\,z=z_{0}+r\cos \theta \,$

Ver também

• Esfera tridimensional

Ligações externas

• Livro Cônicas e Quádricas: Livro do Prof. Jacir J. Venturi, de 246 páginas, disponível na íntegra para acesso gratuito.