Lema do bombeamento para linguagens regulares
O lema do bombeamento para linguagens regulares descreve uma propriedade essencial de todas as linguagens regulares: todas as cadeias suficientemente longas duma dada linguagem regular podem ser "bombeadas", isto é, cada uma dessas cadeias tem uma subcadeia central que pode ser repetida arbitrariamente a fim de produzir uma nova cadeia que também pertence à mesma linguagem.
O lema do bombeamento foi primeiro enunciado por Y. Bar-Hillel, Micha Perles e Eli Shamir em 1961.[1] Ele é útil para provar que uma linguagem não é regular. Há vários outros lemas do bombeamento, todos com objetivos similares.
Enunciado formal
[editar | editar código-fonte]Seja L uma linguagem regular. Então existe um inteiro p ≥ 1 (chamado "comprimento de bombeamento") tal que cada cadeia w de L com comprimento maior ou igual a p pode ser escrita como w = xyz (i.e. w pode ser dividida em três subcadeias) satisfazendo as seguintes condições:
- |y| ≥ 1
- |xy| ≤ p
- para todo i ≥ 0, xyiz ∈ L
y é a subcadeia que pode ser bombeada (removida ou repetida arbitrariamente).
Descrição das condições:
- Para poder ser bombeada, y precisa ter comprimento maior ou igual a 1;
- y precisa estar entre os p primeiros caracteres;
- Podemos repetir arbitrariamente (e inclusive omitir) a subcadeia y, e a cadeia xyz resultante pertencerá a L.
Expressão formal
[editar | editar código-fonte]
Enunciado informal
[editar | editar código-fonte]O lema do bombeamento descreve uma propriedade fundamental das linguagens regulares: para qualquer linguagem regular L, existe um número p tal que qualquer cadeia w de comprimento igual ou maior que p pode ser dividida em três subcadeias, , tal que a parte do meio (não-vazia), y, pode ser repetida um número arbitrário de vezes (inclusive 0 vezes, o que significa remover y), gerando uma nova cadeia que também pertence a L.
Esse processo de repetição é conhecido como "bombeamento". O lema do bombeamento garante ainda que o comprimento de xy será no máximo p, o que limita as maneiras em que w pode ser dividida.
É importante notar que linguagens finitas (aquelas que são reconhecidas por um autômato finito) satisfazem o lema do bombeamento por vacuidade, isto é, a maior cadeia pertencente à linguagem é menor que o p dessa linguagem. Deste modo, o lema não pode ser aplicado a nenhuma das palavras dessa linguagem, pois todas as cadeias são menores que p (lembrando que só cadeias de comprimento ao menos p podem ser bombeadas). Então, como não é possível encontrar um contra-exemplo, não existe contradição, e o lema também se aplica a linguagens finitas.
Uso do lema
[editar | editar código-fonte]O lema do bombeamento é frequentemente usado para provar que uma certa linguagem é não-regular: faz-se uma prova por contradição obtendo uma cadeia dessa linguagem que não obedeça ao lema, isto é, uma cadeia de tamanho pelo menos p que, em se aplicando o bombeamento, forneça uma cadeia que não pertença à linguagem em questão.
Exemplo: podemos provar que a linguagem L = {anbn : n ≥ 0} do alfabeto Σ = {a, b} é não-regular por contradição. Sejam w, x, y, z, p, e i como descritos anteriormente. Seja w = apbp. Pelo lema do bombeamento, há de haver uma cadeia w = xyz com |xy| ≤ p e |y| ≥ 1 tal que xyiz pertence a L para todo i ≥ 0. Pela condição |xy| ≤ p do lema do bombeamento, sabemos que y consiste apenas de instâncias de a (já que definimos w = apbp). Fazendo o bombeamento xy2z, obtemos uma cadeia que tem mais instâncias da letra a que da letra b, uma vez que adicionamos instâncias da letra a sem acrescentar novas instâncias da letra b (já que y é composto inteiramente de letras a). Logo, xy2z não pertence a L, o que é uma contradição. Portanto, a suposição de que L é regular está incorreta.
Prova
[editar | editar código-fonte]Para toda linguagem regular, há um autômato finito determinístico (AFD) que aceita a linguagem. Podemos construir vários autômatos finitos distintos (mas equivalentes) para reconhecer a mesma linguagem, portanto vamos considerar o autômato finito mais simples possível, isto é, aquele com o menor número de estados possível. A quantidade de estados desse AFD é usado como o p da linguagem que ele reconhece. Para uma cadeia de comprimento igual ou maior que p, seja s0 o estado inicial e s1, ..., sp a seqüência dos próximos p estados do AFD conforme a cadeia é lida. Exatamente porque o AFD tem apenas p estados, nesta seqüência de p + 1 estados visitados deverá haver ao menos um estado "repetido", i.e. visitado mais de uma vez. Chamemos esse estado de S. Entre a primeira e a segunda visita a S, o AFD seguiu uma série de transições que correspondem a uma subcadeia, que chamaremos de y.
Uma vez que o AFD garantidamente visita S ao menos uma vez, não precisamos voltar a S novamente, portanto o AFD não precisa passar pelos estados intermediários representados pela subcadeia y. De modo semelhante, já que o AFD sempre volta a S após seguir as transições representadas por y, segue que podemos repetir y um número arbitrário de vezes. As condições do lema estão satisfeitas.
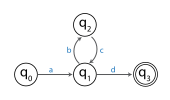
Exemplo:
O autômato aceita a cadeia abcd. Essa cadeia tem um comprimento igual ao número de estados do autômato (quatro): o Princípio da casa dos pombos aponta que deve haver ao menos um estado repetido no autômato. Neste exemplo, o único estado repetido é q1.
Já que a leitura da subcadeia bc resulta em transições que iniciam e terminam em q1, essa subcadeia pode ser repetida: o autômato aceita, por exemplo, a cadeia abcbcd. A subcadeia bc também poderia ser removida e a cadeia resultante ad ainda seria aceita. Usando a notação do lema do bombeamento, a cadeia abcd é dividida entre um x (a), um y (bc) e um z (d).
Não-suficiência
[editar | editar código-fonte]O lema do bombeamento não é uma condição necessária e suficiente para a regularidade de uma linguagem: se o lema não é satisfeito numa dada linguagem L, então L não é regular, mas se o lema é satisfeito para uma dada linguagem L, então L pode ou não ser regular.
Para uma prova completa de regularidade de linguagens, veja o Teorema de Myhill-Nerode. Para se provar que uma linguagem é regular, geralmente se constrói um autômato finito ou uma expressão regular para a linguagem.
Ver também
[editar | editar código-fonte]Notas e referências
- ↑ Y. Bar-Hillel, M. A. Perles, E. Shamir, “On formal properties of simple phrase structure grammars”, Zeitschrift für Phonetik, Sprachwissenschaft und Kommunikationsforschung 14 (1961) pp. 143-172.
Referências
[editar | editar código-fonte]- Michael Sipser (1997). Introduction to the Theory of Computation. [S.l.]: PWS Publishing. ISBN 0-534-94728-X Section 1.4: Nonregular Languages, pp. 77–83.
- John E. Hopcroft and Jeffrey D. Ullman, Introduction to Automata Theory, Languages, and Computation, Addison-Wesley Publishing, Reading Massachusetts, 1979. ISBN 0-201-02988-X. (Veja capítulo 3.)