Logit

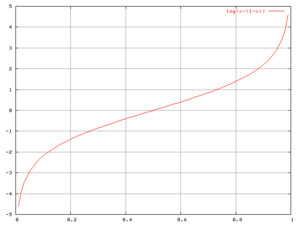
Em matemática, especialmente aquelas aplicadas em estatística, o logit de um número p entre 0 e 1 é

$\operatorname{logit}(p)=\log\left( \frac{p}{1-p} \right) =\log(p)-\log(1-p). \!\,$

(A base da função logaritmo usada aqui é de pouca importância no presente artigo, dado que é maior que 1, ainda que o logaritmo natural com base e é normalmente usado.) A função 'logit é a inversa do "sigmóide", ou função "logística".

Se p é uma probabilidade de sucesso em um determinado evento, então p/(1 − p) é a correspondente razão de chance do mesmo. Logo logit da probabilidade é o logaritmo dos odds; similarmente a diferença entre os logits de duas probabilidades é o logaritmo da razão de chance, obtendo-se assim um mecanismo aditivo para combinar razões de chance:

$\operatorname{log}(OR)=\log\left( \frac{{p}/{1-p}}{{q}/{1-q}} \right) =\log\left( \frac{p}{1-p} \right) - \log\left(\frac{q}{1-q}\right)=\operatorname{logit}(p)-\operatorname{logit}(q). \!\,$

Gráfico de logit na faixa 0 a 1, a base é e

Referências

• J. S. Cramer (2003). "The origins and development of the logit model" (em inglês)