Tabela Price

Tabela Price, também chamado de sistema francês de amortização, é um método usado em amortização de empréstimo cuja principal característica é apresentar prestações (ou parcelas) iguais. O método foi apresentado em 1771 por Richard Price em sua obra "Observações sobre Pagamentos Remissivos" (em inglês: Observations on Reversionary Payments).

O método foi idealizado pelo seu autor para pensões e aposentadorias. No entanto, foi a partir da 2ª revolução industrial que sua metodologia de cálculo foi aproveitada para cálculos de amortização de empréstimo.

Cálculo

A Tabela Price usa o regime de juros compostos para calcular o valor das parcelas de um empréstimo e, dessa parcela, qual é o valor relativo ao pagamento de juros e qual é relativo à amortização do empréstimo.

Tomemos como exemplo um empréstimo de $ 1 000,00 com taxa de juros de 3% ao mês a ser pago em 4 parcelas mensais. Para calcular o valor da parcela, deve-se usar a fórmula de cálculo de parcelas de mesmo valor:

$pmt={\frac {PV\times i}{1-{\frac {1}{\left(1+i\right)^{n}}}}}$

sendo, então:

$pmt={\frac {1000\times 0,03}{1-{\frac {1}{\left(1+0,03\right)^{4}}}}}\approx 269,03$

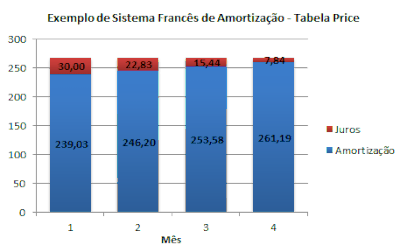
Um mês depois do empréstimo, o saldo devedor cresce 3% indo para $ 1 030,00, porém, como também deve ocorrer o pagamento de $ 269,03, o saldo devedor passa a ser $ 760,97. Perceba que o pagamento da parcela cobriu os juros de $ 30,00 e também fez a amortização de $ 239,03 (1 000,00 - 760,97) do valor emprestado. O mesmo ocorre nos meses seguintes, porém, como o saldo devedor diminui a cada mês, o valor das parcelas relativo ao pagamento dos juros é decrescente.

Período $n$	Saldo Devedor $PV$ - A	Parcela $pmt$	Juros $J$	Amortização (A) $pmt-J$
0	1 000,00
1	760,97	269,03	30,00	239,03
2	514,77	269,03	22,83	246,20
3	261,19	269,03	15,45	253,58
4	0,00	269,03	7,84	261,19

• Em Price, a expressão ${(1+i)^{n}*i} \over {(1+i)^{n}-1}$ é chamada de Fator de Recuperação de Capital.

Amortizações em Price

No sistema Price, os valores das amortizações obedecem a uma progressão geométrica em função do Fator de Rendimento, conforme a expressão $A_{n}=A_{1}\cdot (1+i)^{n-1}$.

Demonstração:

A partir do exemplo anterior, com taxa de 3% a.m. e valor da 1ª amortização $A_{1}=239,03$, então, o valor da 4ª amortização se dá conforme: $A_{4}=239,03\cdot (1+0,03)^{4-1}=261,19$.

Descapitalização das parcelas no tempo

A fórmula de cálculo para o Valor Presente $(PV)$, em Price, é equivalente às somas das descapitalizações das parcelas $(pmt)$ no tempo, conforme as expressões a seguir:

$PV={\frac {pmt}{\frac {(1+i)^{n}*i}{(1+i)^{n}-1}}}=\sum _{\text{j=1}}^{n}{\frac {pmt}{(1+i)^{j}}}$

Demonstração

Tomando por base o exemplo anterior, onde o montante de $ 1.000,00 à taxa de 3% a.m., durante 4 meses, resultando na parcela de $ 269,03 ao mês, a soma das descapitalizações dessas parcelas se dá conforme a seguir:

$1000,00\approx {\frac {269,03}{(1+0,03)^{1}}}+{\frac {269,03}{(1+0,03)^{2}}}+{\frac {269,03}{(1+0,03)^{3}}}+{\frac {269,03}{(1+0,03)^{4}}}$

Nesse exemplo, o montante inicial se equipara às descapitalizações das parcelas pagas em cada período trazidas para a data presente, demonstrando, portanto, o valor presente líquido (VPL) do financiamento e a equivalência com o cálculo de Richard Price. Uma demonstração rigorosa de tal fórmula pode ser encontrada neste link.

Juros em Price

A partir da formulação anterior, pode-se achar uma expressão para as parcelas mensais de juros. De fato, o montante de juros a ser pago no mês $k$ recai sobre o Valor Presente do mês anterior, $PV_{k-1}$, assim, temos

$J_{k}=PV_{k-1}\cdot i$.

Sobre a natureza dos juros

Não existem questionamentos sobre se a Tabela Price emprega juros simples ou juros compostos.

Richard Price, criador do método, afirma que suas tabelas são construídas por juros compostos (p.262-287, 1 803-1 812), jamais mencionando a existência de cobrança de juros sobre juros acumulados no empréstimo. Ainda, em julho de 2004, diversos autores de matemática financeira do Brasil assinaram um manifesto afirmando que a Tabela Price é construída com base no regime de capitalização por juros compostos

Autores afirmam que o Sr. Price tomou as Tabelas de Juro Composto já existentes e incorporou ao seu livro para poupar os seus leitores de procurá-las em outros livros.

Destaca-se também que Calculadora do Cidadão, aplicativo elaborado pelo Banco Central do Brasil, descreve a referida metodologia como concebida pelo regime de juros compostos.

Ver também

• Sistema de Amortização Constante (SAC)
• Sistema de Amortização Misto (SAM / SACRE)
• Sistema de Amortização Americano
• Método de Equivalência a Juros Simples (MEJS)

Bibliografia

• BOYER, C. História da matemática. São Paulo, Edgard Blücher, 2002.
• CAVALHEIRO, Luiz A.F. Elementos de Matemática Financeira. Rio de Janeiro, Editora FGV, 11a ed., 1989.
• NOGUEIRA, José Jorge Meschiatti. Tabela Price: da Prova Documental e Precisa Elucidação do seu Anatocismo, Servanda Ed., 2002.
• NOGUEIRA, José Jorge Meschiatti. Tabela Price: Mitos e Paradigma Ed.Millennium, 2008.
• PEREIRA, Ernesto Luiz de Assis. Amortização de financiamentos por juros simples para o Sistema Financeiro da Habitação. Modelo de Gauss. No prelo
• PRICE, Richard. Observations on Reversionary Payments. Londres: Ed. T. Cadell, 4ª ed., 1783; 6ª ed., 1803; e 7ª ed., 1812.
• ROVINA, Edson. Tabela Price- verdades que incomodam. Disponível em <http://www.procon.sp.gov.br> capturado em 08/2007.
• SILVA, André Luiz Carvalhal. Matemática financeira aplicada. São Paulo: Ed. Atlas, 2005.
• CAMPOS FILHO, Ademar et al. Declaração em defesa de uma Ciência Matemática e Financeira. Disponível no site do Sindicato dos Economistas do Estado de São Paulo, www.sindecon-esp.org.br/force_download.php?file=arq_sys/neodownload/defesa150704.pdf&name=defesa 150704.pdf. Acesso em 9/2006.
• LEWIN, F. I. A.; Early, F.S.S, N. Book on Compound Interest, Richard Witt’s Arithmeticall Questions. JIA, 1970, p. 121-132.
• FIGUEIREDO, Alcio Manoel de Sousa. Tabela Price & Capitalização de Juros. Editora: Juruá ,2004

Ligações externas

• Comparação entre sistemas de Amortização (SAC, SACRE, PRICE, MEJS)