Ângulo de incidência

Ângulo de incidência é uma medida de desvio de um ângulo formado entre o feixe de luz que incide sobre o objeto e a normal; a normal é um segmento que forma com a superfície com um ângulo de 90º, por exemplo:
- na abordagem de um raio de uma superfície;
- o ângulo no qual a asa ou cauda horizontal de um avião é instalado na fuselagem, medido em relação ao eixo da fuselagem.
Ótica[editar | editar código-fonte]
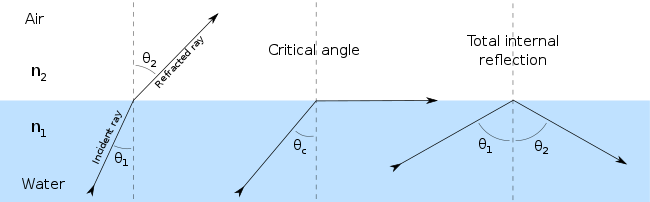
Em ótica geométrica, o ângulo de incidência é o ângulo entre um raio incidente sobre uma superfície e a linha perpendicular à superfície no ponto de incidência, a chamada normal. O raio pode ser formado por qualquer onda: ótica, acústica, micro-onda, raio X e assim por diante. Na figura acima, a linha vermelha representa um raio que faz um ângulo θ com a normal (linha pontilhada). O ângulo de incidência com que a luz é primeiro totalmente refletida internamente é conhecido como ângulo crítico. Ângulo de reflexão e ângulo de refração são outros ângulos relacionados com feixes.
Ângulo de visão[editar | editar código-fonte]
Ao lidar com um feixe que é quase paralelo a uma superfície, por vezes é mais útil para se referir ao ângulo entre o feixe e a superfície, e que a distância entre o feixe e a superfície normal , por outras palavras, 90 ° menos o ângulo de incidência. Este pequeno ângulo é chamado de ângulo de visão ou ângulo de pastagem. Incidência em ângulos de pastagem é chamada de "incidência rasante".
A incidência de difração é usado em espectroscopia de raios-X e átomo óptica, onde a reflexão significativa pode ser alcançada apenas com pequenos valores do ângulo de pastagem. Espelhos Ridged são projetados para a reflexão de átomos próximos ao ângulo de pastagem. Este ângulo é geralmente medido em miliradianos.
A determinação do ângulo de pastagem com relação a uma superfície plana é trivial, mas o cálculo para quase qualquer outra superfície é significativamente mais difícil. A solução exata para uma esfera (que tem importantes aplicações em astronomia e computação gráfica) foi um problema em aberto por quase 50 anos até que um resultado de forma fechada foi derivado por matemáticos Allen R Miller e Emanuel Vegh em 1991.[1]
[editar | editar código-fonte]
Em aviões de asa fixa, o ângulo de incidência (por vezes referido como o ângulo de montagem)[2] é o ângulo entre a linha de corda da asa, onde a asa é montada para a fuselagem, e um eixo de referência ao longo da fuselagem (frequentemente a direção da resistência mínima, ou, quando aplicável, o eixo longitudinal). O ângulo de incidência é fixado no projeto da aeronave, e com raras exceções, não podem ser variadas em vôo.[3]
Reflexão da luz[editar | editar código-fonte]
Reflexão de luz ou é especular (espelhado) ou difusa (retendo a energia, mas perdendo a imagem), dependendo da natureza da interface. Além disso, se a interface estiver entre um dielétrico e um condutor a fase da onda refletida é mantida, de outro modo, se a interface estiver entre dois dielétricos a fase pode ser retida ou ser invertida, dependendo dos índices de refração.
Um espelho fornece o modelo mais comum para a reflexão de luz especular e consiste tipicamente de uma folha de vidro com um revestimento metálico, onde a reflexão ocorre realmente. A reflexão é reforçada em metais pela supressão de propagação da onda além de suas profundezas da pele. Reflexo também ocorre na superfície dos meios transparentes, tais como água ou vidro.

No diagrama à esquerda, um PO raio de luz atinge um espelho vertical no ponto O, e o raio refletido é OQ. Ao projetar uma linha imaginária que passa pelo ponto S perpendicular ao espelho, conhecido como a normal, que pode medir o ângulo de incidência, θi e o ângulo de reflexão, θr. A lei da reflexão diz que θi = θr ou, por outras palavras, o ângulo de incidência é igual ao ângulo de reflexão.
De fato, a reflexão de luz pode ocorrer sempre que a luz se propaga a partir de uma média de um determinado índice de refração no meio com um índice de refração diferente. No caso mais geral, uma certa fração da luz é refletida da interface, e o restante é refratada. Resolvendo as equações de Maxwell, um raio de luz que atinge um limite permite a derivação das equações de Fresnel, que podem ser utilizadas para prever a quantidade de luz é refletida, e quanto é refratada para uma dada situação. A reflexão interna total da luz a partir de um meio mais denso ocorre se o ângulo de incidência for superior ao ângulo crítico.
A reflexão interna total é utilizada como um meio de se concentrar as ondas que não podem efetivamente ser refletidas por meios comuns. Telescópios de raios X, são construídos através da criação de um "túnel" convergente para as ondas. À medida que as ondas interagem com baixo ângulo com a superfície do túnel são refletidas em direção ao ponto do foco (ou para outra interação com a superfície do túnel, eventualmente, a serem dirigidas para o detector no foco). Um refletor convencional seria inútil, já que os raios-X simplesmente passam pelo refletor pretendido.
Quando a luz se reflete em um material mais denso (com maior índice de refração) do que o meio externo, ele sofre uma inversão de polaridade (fase). Em contraste, um material de menor índice de refração (menos denso) irá refletir a luz em fase. Este é um princípio importante no campo da óptica de película fina.
A reflexão especular forma imagens. Reflexão a partir de uma superfície plana forma uma imagem no espelho, o que parece ser invertida da esquerda para a direita porque nós comparamos a imagem que vemos ao que gostaríamos de ver se estivéssemos girados para a posição da imagem. Reflexão especular em uma superfície curva forma uma imagem que pode ser ampliada ou reduzida, e deformada. Espelhos curvos têm potência óptica. Estes espelhos podem ter superfícies que são esféricas ou parabólicas.
Índice de Refração[editar | editar código-fonte]

Índice de refração é uma relação entre a velocidade da luz no vácuo (c) e a velocidade da luz em um determinado meio. Em meios com índices de refração mais baixos (próximos a 1) a luz tem velocidade maior (ou seja, próximo a velocidade da luz no vácuo). A relação pode ser descrita pela fórmula:
Em que: c é a velocidade da luz no vácuo (c = 3 x m/s); v é a velocidade da luz no meio;
De modo geral, a velocidade da luz nos meios materiais é menor que c; e assim, em geral, teremos n > 1. Por extensão, definimos o índice de refracção do vácuo, que obviamente é igual a 1. Portanto, sendo n o índice de refracção de um meio qualquer, temos:
A velocidade de propagação da luz no ar depende da frequência da luz, já que o ar é um meio material. Porém, essa velocidade é quase igual a c = 3 x m/s para todas as cores. Ex.: índice de refracção da luz violeta no ar = 1,0002957 e índice de refracção da luz vermelha no ar = 1,0002914. Portanto, nas aplicações, desde que não queiramos uma precisão muito grande, adoptaremos o índice de refracção do ar como aproximadamente igual a 1:
Como vimos, as cores, por ordem crescente de frequências, são: vermelho, laranja, amarelo, verde, azul, índigo (anil) e violeta.
A experiência mostra que, em cada meio material, a velocidade diminui com a frequência, isto é, quanto "maior" a frequência, "menor" a velocidade.
Portanto como , concluímos que o índice de refracção aumenta com a frequência. Quanto "maior" a frequência, "maior" o índice de refracção.
Referências
- ↑ Allen R Miller e Emanuel Vegh (1993). "Resultado exato para o ângulo de refração de reflexão especular de uma esfera". SIAM revisão 35 :. 472-480 doi : 10.1137/1035091.
- ↑ Phillips, Warren F. (2010). Mecânica de Vôo (2 ª ed.). Wiley & Sons. ISBN 978-0-470-53975-0
- ↑ Kermode, AC (1972), Mecânica de Vôo , capítulo 3, 8 ª edição, Pitman Publishing, Londres. ISBN 0-273-31623-0






