Espiral de Cornu

A espiral de Cornu, também conhecida como clotóide e como espiral de Euler e radioide dos arcos, é uma curva cuja curvatura varia linearmente ao longo de seu comprimento. A espiral de Cornu foi criada por Marie Alfred Cornu como um nomograma para os cálculos de difração na ciência e na engenharia. Em projectos de engenharia rodoviária, esta espiral é largamente utilizada como curva de transição com o principal objectivo de ligar geometricamente uma recta e uma curva circular. Esta curva assegura um decrescimento linear da curvatura com o caminho percorrido ao longo do seu desenvolvimento, proporcionando assim uma variação gradual do raio de curvatura. Daqui resulta então:
- A sua curvatura começa em zero no ponto osculador com o alinhamento recto e aumenta linearmente à medida que se percorre o desenvolvimento da curva.
- Quando a espiral/clotóide encontra a curva circular no respectivo ponto de osculação, a sua curvatura é igual á da curva circular.
A espiral de Cornu é gerada pelo desenho paramétrico de S(x) contra C(x), em que:
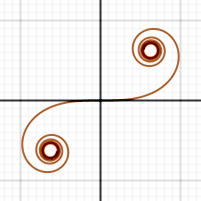
{C(x), S(x)} (Note que a espiral converge para o centro dos buracos na imagem acima conforme x tenta a infinito e a menos infinito.)
Seguindo a curva, o comprimento da curva de {S(0), C(0)} a {S(x), C(x)} deve ser igual a x, já que S′(x)² + C′(x)² = 1. O comprimento total da curva (de x = −∞ para ∞) é portanto infinito.


