Hamming (7,4)

Em teoria de codificação, Hamming (7,4) é um código de correcção de erros linear que codifica 4 bits de dados em bits de 7 por adição de 3 bits de paridade. É um membro da grande família dos códigos de Hamming, mas o termo código de Hamming refere-se geralmente a este código específico que Richard W. Hamming introduzido em 1950. Nessa época, Hamming trabalhava no Bell Telephone Laboratories e andava frustrado com os erros provocados pelos leitores de cartões perfurados, tendo por isso começado a trabalhar em códigos de correcção de erro.[1]

O código de Hamming adiciona três bits de verificação a cada quatro bits de dados da mensagem. O algoritmo de Hamming (7,4) pode corrigir qualquer erro de um único bit, ou detectar todos os erros de um e dois bits. Noutras palavras, a distância de Hamming mínima entre quaisquer duas palavras de código corretas é 3, e as palavras recebidas podem ser correctamente descodificadas se estiverem a uma distância máxima de 1 da palavra de código que foi enviada pelo transmissor. Isto significa que, para as situações em que não ocorrem erros de burst, o código Hamming (7,4) é suficiente (O canal teria de ser extremamente ruidoso para alterar 2 dos 7 bits).

Objectivo

Representação gráfica dos 4 bits de dados $d_{1}$ a $d_{4}$ e 3 bits de paridade $p_{1}$ a $p_{3}$ e a respectiva correspondência.

O objectivo do código de Hamming é criar um conjunto de bits de paridade, que se sobrepõem de tal forma que um erro num único bit (de dados ou paridade) pode ser detectado e corrigido. Embora possam ser criadas múltiplas sobreposições, existe um método geral apresentado em código de Hamming.

Bit #	1	2	3	4	5	6	7
Bit transmitido	$p_{1}$	$p_{2}$	$d_{1}$	$p_{3}$	$d_{2}$	$d_{3}$	$d_{4}$
$p_{1}$	Sim	Não	Sim	Não	Sim	Não	Sim
$p_{2}$	Não	Sim	Sim	Não	Não	Sim	Sim
$p_{3}$	Não	Não	Não	Sim	Sim	Sim	Sim

Esta tabela descreve a cobertura efectuada pelos bits de paridade. Por exemplo, $p_{2}$ fornece um controlo de paridade os bits 2, 3, 6, e 7. Numa leitura em coluna podemos observar que o bit $d_{1}$ é coberto pelos bits de paridade $p_{1}$ e $p_{2}$. Esta tabela tem uma grande semelhança com a matriz de paridade $H$ da próxima secção.

Se as colunas correspondentes aos bits de paridade foram removidas da tabela acima, temos:

	$d_{1}$	$d_{2}$	$d_{3}$	$d_{4}$
$p_{1}$	Sim	Sim	Não	Sim
$p_{2}$	Sim	Não	Sim	Sim
$p_{3}$	Não	Sim	Sim	Sim

Assim, escolhendo correctamente a cobertura dos bits de paridade, todos os erros com distância Hamming de 1 podem ser detectados e corrigidos, que é o objectivo da utilização de um código de Hamming.

Matrizes

Os códigos de Hamming podem ser calculados com recurso à álgebra linear através de matrizes, porque são códigos lineares. Para efeito dos códigos Hamming, devem ser definidas duas matrizes: A matriz geradora do código $G$ e a matriz de paridade $H$:

$\mathbf {G} :={\begin{pmatrix}1&1&0&1\\1&0&1&1\\1&0&0&0\\0&1&1&1\\0&1&0&0\\0&0&1&0\\0&0&0&1\\\end{pmatrix}}$

e

$\mathbf {H} :={\begin{pmatrix}1&0&1&0&1&0&1\\0&1&1&0&0&1&1\\0&0&0&1&1&1&1\\\end{pmatrix}}$

Posição dos bits de dados e paridade

As linhas 1, 2 e 4 de $G$ são familiares porque mapeiam os bits de dados para os respectivos bits de paridade:

• $p_{1}$ cobre $d_{1}$, $d_{2}$, $d_{4}$
• $p_{2}$ cobre $d_{1}$, $d_{3}$, $d_{4}$
• $p_{3}$ cobre $d_{2}$, $d_{3}$, $d_{4}$

As linhas restantes (3, 5, 6 e 7) mapeiam os dados para a sua posição em formato codificado, só havendo 1 por linha estas quatro linhas são linearmente independentes e formam a matriz identidade. As linhas da matriz $H$ são utilizadas para calcular o síndroma da mensagem, se o síndroma é o vector nulo (tudo zeros), então a palavra recebida não tem erros; se não for nulo, então o valor indica o bit errado.

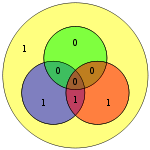
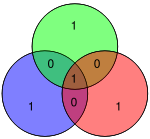
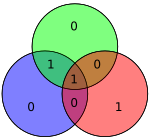
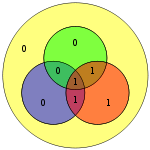
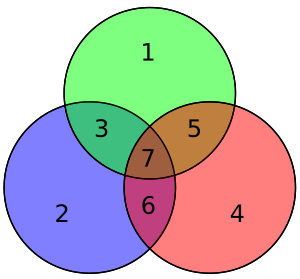
Os 4 bits de dados, representados como vector P, é multiplicada por G usando modulo 2, para se obter o valor codificado que vai ser transmitido. Os 4 bits de dados originais são convertidos em 7 com 3 bits de paridade adicionados para assegurar as coberturas descritas anteriormente. A tabela acima mostra o mapeamento entre dados e bits de paridade na sua posição final (1 a 7), mas estes também pode ser apresentados num diagrama de Venn. O primeiro diagrama neste artigo mostra três círculos (um para cada bit de paridade) e inclui bits de dados que cada bit de paridade cobre. O segundo diagrama (à direita) é idêntico, mas com as posições de cada bits marcadas.

Durante o resto desta explicação os seguintes 4 bits (mostrado como vector coluna) serão usados como exemplo:

$\mathbf {p} ={\begin{pmatrix}d_{1}\\d_{2}\\d_{3}\\d_{4}\\\end{pmatrix}}={\begin{pmatrix}1\\0\\1\\1\end{pmatrix}}$

Codificação

Mapeamento do exemplo $x$. A paridade dos círculos vermelho, verde e azul é par.

Vamos supor que queremos transmitir o vector $p$ através de um canal de comunicação ruidoso. Um Canal binário simétrico, o que significa que o erro não favorece o valor zero ou um. Além disso, todos os vectores de código são assumidos como sendo equiprováveis. Tomamos o produto de $G$ e $p$ módulo 2, para determinar a palavra de código a transmitir $x$:

$\mathbf {x} =\mathbf {G} \mathbf {p} ={\begin{pmatrix}1&1&0&1\\1&0&1&1\\1&0&0&0\\0&1&1&1\\0&1&0&0\\0&0&1&0\\0&0&0&1\\\end{pmatrix}}{\begin{pmatrix}1\\0\\1\\1\end{pmatrix}}={\begin{pmatrix}2\\3\\1\\2\\0\\1\\1\end{pmatrix}}={\begin{pmatrix}0\\1\\1\\0\\0\\1\\1\end{pmatrix}}$

Isto significa que 0110011 será transmitido em vez de 1011.

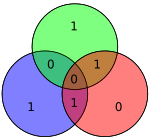
No diagrama à direita, os 7 bits da palavra codificada são inseridos nas suas respectivas posições, observando as paridades, é evidente que a paridade do vermelho, verde e azul é par:

• círculo vermelho tem dois 1
• círculo verde tem dois 1
• círculo azul tem quatro 1

O que vamos observar seguidamente é que, se durante a transmissão um bit for invertido a paridade de 2 ou 3 círculos será incorrecta e o bit com erro pode ser determinado (mesmo se for um dos bits de paridade), sabendo que a paridade dos três círculos deve ser par.

Paridade

Se não ocorrer um erro durante a transmissão, a palavra de código recebida $r$ é idêntica à palavra transmitida $x$:

$\mathbf {r} =\mathbf {x}$

O receptor multiplica $H$ e $r$ para obter o vector $\mathbf {z}$ denominado síndroma, que indica se ocorreu um erro, e se assim for, qual o bit da palavra de código que o contém. Realizar esta multiplicação com módulo 2.

$\mathbf {z} =\mathbf {H} \mathbf {r} ={\begin{pmatrix}1&0&1&0&1&0&1\\0&1&1&0&0&1&1\\0&0&0&1&1&1&1\\\end{pmatrix}}{\begin{pmatrix}0\\1\\1\\0\\0\\1\\1\end{pmatrix}}={\begin{pmatrix}2\\4\\2\end{pmatrix}}={\begin{pmatrix}0\\0\\0\end{pmatrix}}$

Como o síndroma $z$ é o vector nulo, o receptor pode concluir que não ocorreu nenhum erro. Esta conclusão é baseada na observação de que quando o vector de dados é multiplicada por $G$, ocorre uma mudança de base para um sub-espaço vectorial que é o núcleo de $H$. Desde que nada aconteça durante a transmissão, $\mathbf {r}$ permanecerá no núcleo de $H$ e multiplicação irá produzir o vector nulo.

Correcção de erros

Caso contrário, vamos supor que ocorreu um erro num bit. Matematicamente, podemos escrever:

$\mathbf {r} =\mathbf {x} +\mathbf {e} _{i}$

Onde $e_{i}$ é a posição $i$ do vector, ou seja, um vector nulo com um 1 na posição $i$.

$e_{2}={\begin{pmatrix}0\\1\\0\\0\\0\\0\\0\end{pmatrix}}$

Assim, a expressão acima significa um erro de um único bit na posição $e_{i}$.

Se multiplicarmos pelo vector $H$:

$\mathbf {Hr} =\mathbf {H} \left(\mathbf {x} +\mathbf {e} _{i}\right)=\mathbf {Hx} +\mathbf {He} _{i}$

Por exemplo, suponhamos que introduzimos um erro no bit #5

$\mathbf {r} =\left(\mathbf {x} +\mathbf {e} _{5}\right)=\left({\begin{pmatrix}0\\1\\1\\0\\0\\1\\1\end{pmatrix}}+{\begin{pmatrix}0\\0\\0\\0\\1\\0\\0\end{pmatrix}}\right)={\begin{pmatrix}0\\1\\1\\0\\1\\1\\1\end{pmatrix}}={\begin{pmatrix}0\\1\\1\\0\\1\\1\\1\end{pmatrix}}$

Um erro no bit 5 causa paridade errada no circulo vermelho e verde

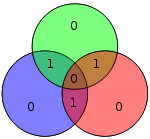
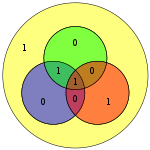
O diagrama à direita mostra o bit com erro (a azul) e a nova paridade criada (a vermelho) nos círculos vermelho e verde. O bit de erro pode ser detectado pelo cálculo da paridade dos círculos vermelho, verde e azul. Se uma paridade errada é detectada, então o bit de dados que se sobrepõe aos círculos de paridade errada está com erro. No exemplo acima, os círculos vermelho e verde têm paridade errada, então o bit correspondente à intersecção entre o vermelho e o verde, indica o bit com erro.

$\mathbf {z} =\mathbf {Hr} ={\begin{pmatrix}1&0&1&0&1&0&1\\0&1&1&0&0&1&1\\0&0&0&1&1&1&1\\\end{pmatrix}}{\begin{pmatrix}0\\1\\1\\0\\1\\1\\1\end{pmatrix}}={\begin{pmatrix}3\\4\\3\end{pmatrix}}={\begin{pmatrix}1\\0\\1\end{pmatrix}}$

O que corresponde a quinta coluna da $H$. Além disso, o algoritmo geral usado foi intencionalmente construido, de modo que o síndroma de 101 correspondesse ao valor binário 5, o que indica que o quinto bit está corrompido. Deste modo, um erro é detectado no bit 5, e pode ser corrigido.

$\mathbf {r} _{corrected}={\begin{pmatrix}0\\1\\1\\0\\{\overline {1}}\\1\\1\end{pmatrix}}={\begin{pmatrix}0\\1\\1\\0\\0\\1\\1\end{pmatrix}}$

Este valor, agora corrigido, corresponde ao valor $x$ transmitido no inicio.

Descodificação

Assim que for determinado que o vector recebido está livre de erros ou for corrigido de um erro, será então necessário descodifica-lo de volta à sua forma original de 4 bits.

Em primeiro lugar definimos uma matriz $\mathbf {R}$:

$\mathbf {R} ={\begin{pmatrix}0&0&1&0&0&0&0\\0&0&0&0&1&0&0\\0&0&0&0&0&1&0\\0&0&0&0&0&0&1\\\end{pmatrix}}$

Temos então que o valor recebido $p_{r}$ será:

$\mathbf {p_{r}} =\mathbf {R} \mathbf {r}$

$\mathbf {p_{r}} ={\begin{pmatrix}0&0&1&0&0&0&0\\0&0&0&0&1&0&0\\0&0&0&0&0&1&0\\0&0&0&0&0&0&1\\\end{pmatrix}}{\begin{pmatrix}0\\1\\1\\0\\0\\1\\1\end{pmatrix}}={\begin{pmatrix}1\\0\\1\\1\end{pmatrix}}$

Múltiplos erros

Introdução de erros nos bits 4 e 5 (a azul) e uma paridade errada no circulo verde(a vermelho)

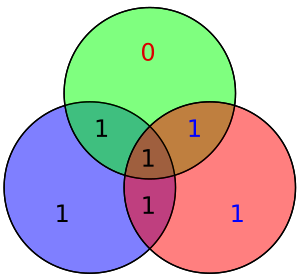
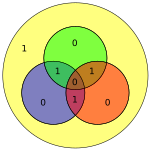
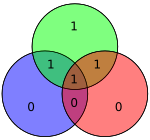
Não é difícil mostrar que apenas os erros de um bit pode ser corrigidos utilizando este esquema. Como alternativa, os códigos de Hamming podem ser utilizados para detectar erros de um ou dois bits, por indicação do produto de $H$ ser diferente de zero quando ocorrem erros. No diagrama da direita, os bits 4 e 5 foram alterados. Isso produz apenas um círculo (verde) com uma paridade inválida, mas os erros não são corrigíveis.

No entanto, o Hamming (7,4) e códigos de Hamming semelhantes não conseguem distinguir entre erros de um bit e de dois. Ou seja, dois erros parecem o mesmo que erros de um bit. Se a correção de erro for realizada num erro de dois bits, o resultado será incorreto.

Palavras válidas

Como a fonte é de 4 bits existem apenas 16 palavras possíveis. A segunda coluna contém o valor a 8 bits se utilizarmos um bit de paridade extra (ver Hamming (7,4) com um bit de paridade adicional). (Os bits de dados são mostrados a azul, os bits de paridade são mostrados a vermelho, e o bit de paridade adicional é mostrado a verde).

Dados $({\color {blue}d_{1}},{\color {blue}d_{2}},{\color {blue}d_{3}},{\color {blue}d_{4}})$	Hamming(7,4)		Hamming(7,4) com bit de paridade extra (Hamming(8,4))
	Transmitido $({\color {red}p_{1}},{\color {red}p_{2}},{\color {blue}d_{1}},{\color {red}p_{3}},{\color {blue}d_{2}},{\color {blue}d_{3}},{\color {blue}d_{4}})$	Diagrama	Transmitido $({\color {red}p_{1}},{\color {red}p_{2}},{\color {blue}d_{1}},{\color {red}p_{3}},{\color {blue}d_{2}},{\color {blue}d_{3}},{\color {blue}d_{4}},{\color {green}p_{4}})$	Diagrama
0000	0000000		00000000
1000	1110000		11100001
0100	1001100		10011001
1100	0111100		01111000
0010	0101010		01010101
1010	1011010		10110100
0110	1100110		11001100
1110	0010110		00101101
0001	1101001		11010010
1001	0011001		00110011
0101	0100101		01001011
1101	1010101		10101010
0011	1000011		10000111
1011	0110011		01100110
0111	0001111		00011110
1111	1111111		11111111