Origem: Wikipédia, a enciclopédia livre.
Em probabilidade e estatística , a distribuição triangular é a distribuição de probabilidade contínua que possui um valor mínimo a , um valor máximo b e uma moda c , de modo que a função densidade de probabilidade é zero para os extremos (a e b ), e afim entre cada extremo e a moda, de forma que o gráfico dela é um triângulo .
A distribuição triangular é uma distribuição muito simples e útil quando se tem poucos dados, conhecendo-se um valor mínimo (a), um valor máximo (b) e um valor mais provável (c) é possível obter uma distribuição triangular que resulta em uma boa aproximação das probabilidades de ocorrência do evento X.
A função densidade de probabilidade é:
f
(
x
|
a
,
b
,
c
)
=
{
2
(
x
−
a
)
(
b
−
a
)
(
c
−
a
)
for
a
≤
x
<
c
2
b
−
a
for
x
=
c
2
(
b
−
x
)
(
b
−
a
)
(
b
−
c
)
for
c
<
x
≤
b
0
for any other case
{\displaystyle f(x|a,b,c)={\begin{cases}{\frac {2(x-a)}{(b-a)(c-a)}}&{\text{for }}a\leq x<c\\&\\{\frac {2}{b-a}}&{\text{for }}x=c\\&\\{\frac {2(b-x)}{(b-a)(b-c)}}&{\text{for }}c<x\leq b\\&\\0&{\text{for any other case}}\end{cases}}}
Parâmetros:
a
:
a
∈
(
−
∞
,
∞
)
{\displaystyle a\colon a\in (-\infty ,\infty )}
b
:
b
>
a
{\displaystyle b\colon b>a}
c
:
a
≤
c
≤
b
{\displaystyle c\colon a\leq c\leq b}
Suporte:
a
≤
x
≤
b
{\displaystyle a\leq x\leq b}
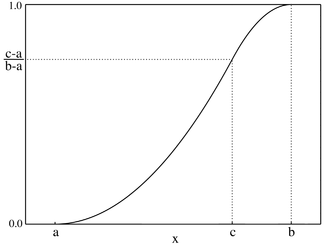
Função de probabilidade acumulada : =
{
(
x
−
a
)
2
(
b
−
a
)
(
c
−
a
)
for
a
≤
x
<
c
c
−
a
b
−
a
for
x
=
c
1
−
(
b
−
x
)
2
(
b
−
a
)
(
b
−
c
)
for
c
<
x
≤
b
{\displaystyle {\begin{cases}{\frac {(x-a)^{2}}{(b-a)(c-a)}}&{\text{for }}a\leq x<c\\&\\{\frac {c-a}{b-a}}&{\text{for }}x=c\\&\\1-{\frac {(b-x)^{2}}{(b-a)(b-c)}}&{\text{for }}c<x\leq b\end{cases}}}
distribuição uniforme pode ser conforme segue abaixo: Digamos que uma determinada empresa precise fazer um investimento, por qualquer que seja o motivo a empresa não conhece exatamente o montante desse investimento, mas conhece o valor mais provável e também os valores mínimo e máximo. Ela estima um valor mais provável para esse investimento em R$2.000.000,00, e estima que o valor mínimo que esse investimento pode assumir é 80% do valor mais provável e que o valor máximo que esse investimento pode assumir é 105% do valor mais provável. Nesse caso temos: c=2.000.000 a=1.600.000 b=2.100.000 Qual seria a probabilidade desse investimento ser de até R$1.800.000,00 ?
F
(
x
<
1.800.000
)
=
(
(
1.800.000
−
1.600.000
)
2
)
/
(
2.100.000
−
1.600.000
)
∗
(
2.000.000
−
1.600.000
)
{\displaystyle F(x<1.800.000)=((1.800.000-1.600.000)^{2})/(2.100.000-1.600.000)*(2.000.000-1.600.000)}
F
(
x
<
1.800.000
)
=
0
,
2
{\displaystyle F(x<1.800.000)=0,2}
F
(
x
<
1.800.000
)
=
20
%
{\displaystyle F(x<1.800.000)=20\%}
Média:
a
+
b
+
c
3
{\displaystyle {\frac {a+b+c}{3}}}
Mediana:
{
a
+
(
b
−
a
)
(
c
−
a
)
2
for
c
≥
b
+
a
2
b
−
(
b
−
a
)
(
b
−
c
)
2
for
c
≤
b
+
a
2
{\displaystyle {\begin{cases}a+{\frac {\sqrt {(b-a)(c-a)}}{\sqrt {2}}}&{\text{for }}c\!\geq \!{\frac {b\!+\!a}{2}}\\&\\b-{\frac {\sqrt {(b-a)(b-c)}}{\sqrt {2}}}&{\text{for }}c\!\leq \!{\frac {b\!+\!a}{2}}\end{cases}}}
Moda:
c
{\displaystyle c\,}
Variância:
a
2
+
b
2
+
c
2
−
a
b
−
a
c
−
b
c
18
{\displaystyle {\frac {a^{2}+b^{2}+c^{2}-ab-ac-bc}{18}}}
Obliquidade :
2
(
a
+
b
−
2
c
)
(
2
a
−
b
−
c
)
(
a
−
2
b
+
c
)
5
(
a
2
+
b
2
+
c
2
−
a
b
−
a
c
−
b
c
)
3
2
{\displaystyle {\frac {{\sqrt {2}}(a\!+\!b\!-\!2c)(2a\!-\!b\!-\!c)(a\!-\!2b\!+\!c)}{5(a^{2}\!+\!b^{2}\!+\!c^{2}\!-\!ab\!-\!ac\!-\!bc)^{\frac {3}{2}}}}}
Curtose :
−
3
5
{\displaystyle -{\frac {3}{5}}}
Entropia:
1
2
+
ln
(
b
−
a
2
)
{\displaystyle {\frac {1}{2}}+\ln \left({\frac {b-a}{2}}\right)}
Função geradora de momentos:
2
(
b
−
c
)
e
a
t
−
(
b
−
a
)
e
c
t
+
(
c
−
a
)
e
b
t
(
b
−
a
)
(
c
−
a
)
(
b
−
c
)
t
2
{\displaystyle 2{\frac {(b\!-\!c)e^{at}\!-\!(b\!-\!a)e^{ct}\!+\!(c\!-\!a)e^{bt}}{(b-a)(c-a)(b-c)t^{2}}}}
Função característica:
−
2
(
b
−
c
)
e
i
a
t
−
(
b
−
a
)
e
i
c
t
+
(
c
−
a
)
e
i
b
t
(
b
−
a
)
(
c
−
a
)
(
b
−
c
)
t
2
{\displaystyle -2{\frac {(b\!-\!c)e^{iat}\!-\!(b\!-\!a)e^{ict}\!+\!(c\!-\!a)e^{ibt}}{(b-a)(c-a)(b-c)t^{2}}}}
A Distribuição Triangular é normalmente usada quando existe uma ideia subjetiva da população, através dos seus extremos e da sua moda.