Distribuição de probabilidade
| Teoria das probabilidades |
|---|
 |
Em teoria da probabilidade e em estatística, uma distribuição de probabilidade descreve o comportamento aleatório de um fenômeno dependente do acaso. O estudo dos fenômenos aleatórios começou com o estudo dos jogos de azar – jogos de dados, sorteios de bolas de urna e cara ou coroa eram motivações para compreender e prever os experimentos aleatórios. Essas abordagens iniciais são fenômenos discretos, o que significa que o número de resultados possíveis é finito ou contável. Entretanto, certas questões revelam distribuições de probabilidade com suporte infinito não contável. Por exemplo, quando o lançamento de uma moeda tende ao infinito, o número de coroas aproxima-se de uma distribuição normal.
Flutuações e variabilidade estão presentes em quase todo valor que pode ser medido durante a observação de um fenômeno, independente de sua natureza, além disso quase todas as medidas possuem uma parte de erro intrínseco. A distribuição de probabilidade pode modelar incertezas e descrever fenômenos físicos, biológicos, econômicos, entre outros. O domínio da estatística permite o encontro das distribuições de probabilidade adaptadas aos fenômenos aleatórios.
Há muitas distribuições de probabilidade diferentes. Entre as distribuições de probabilidade, a distribuição normal tem uma importância particular. De acordo com o teorema central do limite, a distribuição normal aborda o comportamento assintótico de várias distribuições de probabilidade.
O conceito de distribuição de probabilidade é formalizado matematicamente pela teoria da medida – uma distribuição de probabilidade é uma medida muitas vezes vista como uma distribuição que descreve o comportamento de uma variável aleatória discreta ou contínua. Uma medida é uma distribuição de probabilidade se sua massa total for 1. O estudo de uma variável aleatória de acordo com uma distribuição de probabilidade discreta revela o cálculo de somas e de séries, enquanto que o estudo de uma variável aleatória de acordo com uma distribuição de probabilidade absolutamente contínua revela o cálculo de integrais. As funções particulares permitem caracterizar as distribuições de probabilidade como a função de distribuição e a função característica.
Definição informal[editar | editar código-fonte]
Teoricamente uma descrição de probabilidade descreve a característica aleatória de uma experiência aleatória.[1][2] O conceito de experiência aleatória surgiu para descrever um processo real de natureza experimental, em que o acaso intervém com resultados possíveis bem identificados.[3] Por exemplo, em um lançamento de um dado não viciado (um evento aleatório) os resultados podem ser um número entre 1 e 6 com igual probabilidade (de acordo com a distribuição de probabilidade, há a mesma chance de saírem os seis resultados com probabilidade igual a um sexto).
Historicamente distribuições de probabilidade foram estudadas em jogos de azar, jogos de dados, jogos de cartas, entre outros. Se os possíveis resultados dos fenômenos forem números contáveis, a distribuição de probabilidade é chamada discreta. Dar a distribuição de probabilidade significa dar a lista de valores possíveis com suas probabilidades associadas.[1] Ela é dada por meio de uma fórmula, uma tabela de valores, uma árvore de probabilidade ou funções que serão detalhadas nas seções seguintes.
Em um contexto mais amplo, se os números dos resultados possíveis de um fenômeno aleatório forem finitos (contáveis ou incontáveis) em vez de infinitos, a distribuição de probabilidade descreve a distribuição de probabilidade dos resultados possíveis, mas caracterizados como funções (funções densidade, funções distribuição, entre outros) ou como medidas.[1]
Histórico[editar | editar código-fonte]

O uso do acaso existe desde os tempos antigos, especialmente em jogos de azar, em apostas de riscos de transportes marítimos ou em rendas vitalícias.[3] Entretanto, uma das primeiras referências conhecidas para os cálculos de probabilidade é um cálculo elementar sobre a Divina Comédia que aparece apenas no século XV durante o Renascimento.[4] Os primeiros tratados formam o início da teoria da probabilidade, principalmente com base em probabilidades combinatórias. Os problemas surgem à respeito da duração de um jogo de cartas:
| “ | Sobre a duração das partidas em que, começando com um mesmo número de fichas, os jogadores as concedem aos poucos ao oponentes que os vencem em uma partida. Pergunta-se em quantas mãos determinadas a mais acabará a partida que pode durar até o infinito.[5] | ” |
— Pierre Rémond de Montmort, em seu livro Essay d'analyse sur les jeux de hazard. | ||
Reconhece-se a probabilidade (a aposta) de uma variável (a duração de um jogo) ser menor que um valor (um certo número determinado), que representa a função de distribuição da distribuição de probabilidade de um jogo.
Essa é a tese de Nicolau Bernoulli, publicada em 1711, em que aparece pela primeira vez a distribuição uniforme.[6] Então, outras distribuições apareceram como a distribuição binomial e a distribuição normal, embora suas abordagens não sejam completamente rigorosas[6]— por exemplo, a distribuição normal foi desenvolvida por Abraham de Moivre com uma curva de Gauss por uma aproximação numérica.[7] No século XVIII, outras ideias de distribuições de probabilidade emergiram[6] com a expectativa de uma variável aleatória discreta com Jean le Rond D'Alembert ou de probabilidades condicionais com Thomas Bayes. Algumas distribuições de probabilidade contínuas estão contidas em uma memória de Joseph—Louis Lagrange, de 1770.[6]
O uso rigoroso das distribuições de probabilidade começou a partir do século XIX nas ciências aplicadas como na biometria com Karl Pearson[8] ou na física estatística com Ludwing Boltzmann.[9]
A definição formal das medidas de probabilidade surgiu em 1896 com uma publicação de Émile Borel,[10] continuando com outros matemáticos como Henri—Léon Lebesgue, Maurice René Fréchet, Paul Lévy e principalmente Andrei Kolmogorov que formulou os axiomas de probabilidade em 1933.
Definição matemática[editar | editar código-fonte]
Em teoria da probabilidade, uma distribuição de probabilidade é uma medida com massa total igual a 1. Essa medida satisfaz os três axiomas de probabilidade.
Definição[2] — Para um espaço mensurável , é uma distribuição de probabilidade, medida de probabilidade ou simplesmente probabilidade se:
- é uma aplicação de em [0,1];
- ;
- é –aditiva. Isto é, para qualquer família finita ou contável de elementos disjuntos de Uma consequência imediata é: .
é chamado de espaço de probabilidade.[11] Usualmente a palavra distribuição é usada quando tratamos de uma distribuição de probabilidade de uma variável aleatória definida em um espaço de probabilidade .
Definição[12] — Seja uma variável aleatória real no espaço de probabilidade. Isto é, uma função mensurável . A distribuição de probabilidade da variável aleatória é a medida de probabilidade definida sobre o espaço mensurável por para qualquer álgebra de Borel real . Em outras palavras, é a medida de imagem de para .
Então, para definir a distribuição de uma variável aleatória, transpõe-se a distribuição de probabilidade de em uma medida de .
A representação de uma distribuição por uma variável aleatória não é única.[13] Em outras palavras, duas variáveis aleatórias diferentes ou duas variáveis aleatórias definidas em espaços diferentes podem ter a mesma distribuição. Duas variáveis aleatórias reais e têm a mesma distribuição (em termos de igualdade de medidas). Isto é, para todo . O seguinte teorema permite uma caracterização adicional.
Teorema de transferência[14] ou de transporte[15] — Seja uma variável aleatória real . Logo,
para toda função , de tal modo que pelo menos uma das duas integrais existe.[16] A última integral, do ponto de vista da teoria da medida, é uma integral da função em relação à medida . Essa integral tem forma de soma, no caso das distribuições discretas. Então, duas variáveis aleatórias reais e têm a mesma distribuição se para qualquer função , tal que existe pelo menos um dos dois termos da igualdade.
Distribuição multidimensional[editar | editar código-fonte]

Uma distribuição de probabilidade é chamada de multidimensional ou -dimensional[17] quando descreve vários valores (aleatórios) de um fenômeno aleatório, por exemplo, no lançamento de dois dados a distribuição de probabilidade dos dois resultados é uma distribuição bidimensional. Então, a característica multidimensional aparece por meio da transferência por uma variável aleatória de um espaço de probabilidade para um espaço numérico , de dimensão , por exemplo, no lançamento de dois dados a dimensão é e o espaço é . A distribuição multidimensional também é chamada de distribuição conjunta.[18]
Um exemplo importante da distribuição multidimensional é a probabilidade produto , em que e são duas distribuições unidimensionais. Essa distribuição de probabilidade é uma distribuição de um par de variáveis aleatórias independentes.[19] Esse é o caso do exemplo do lançamento de dois dados.
Definição — Seja uma variável aleatória no espaço de probabilidade , com valores em equipada com produtos de algebras de Borel . A distribuição da variável aleatóriaé a medida de probabilidade definida para todo
A variável aleatória é identificada[20] a um vetor aleatório de dimensões : . O teorema de Cramer-Wold[21] estabelece que a distribuição (-dimensional) do vetor aleatório é completamente determinado pelas distribuições (unidimensionais) de todas as combinações lineares dos componentes: para todo .
Distribuição absolutamente contínua[editar | editar código-fonte]

Uma distribuição bidimensional ou -dimensional é chamada de absolutamente contínua[22] em quando a distribuição é absolutamente contínua em relação à medida de Lebesgue em . Isto é, se a distribuição da variável aleatória correspondente é descrita como
,
para todo
Distribuição marginal[editar | editar código-fonte]
Uma distribuição marginal de um vetor aleatório é a distribuição dos seus componentes. Para obter-la, projeta-se a distribuição em um espaço unidimensional de uma coordenada desejada. A distribuição de probabilidade da -ésima coordenada de um vetor aleatório é chamada de -ésima distribuição marginal .[23] A distribuição marginal de é obtida pela fórmula
,
para todo .
As distribuições marginais de uma distribuição absolutamente contínua são expressas com suas densidades marginais.[23]
Distribuição condicional[editar | editar código-fonte]

Uma distribuição de probabilidade condicional permite descrever o comportamento de um fenômeno aleatório quando a informação sobre o processo é conhecida. Em outras palavras, a probabilidade condicional permite avaliar o grau de dependência estocástica entre dois eventos,[24] por exemplo, no lançamento de dois dados a distribuição condicional pode dar a soma dos resultados sabendo que o resultado do lançamento de um dos dois dados foi pelo menos quatro.
Definição para eventos[editar | editar código-fonte]
A probabilidade condicional é definida[25] em eventos pela probabilidade : a probabilidade de um evento A qualquer condicionado a um evento B. Para quaisquer e da σ-álgebra subjacente tal que
.
Em probabilidade e em estatística, a distribuição de probabilidade[26] comumente usada em distribuição da probabilidade total ou no teorema de Bayes.
Definição para variáveis aleatórias[editar | editar código-fonte]
A probabilidade condicional também é definida para as variáveis aleatórias. Seja uma variável X condicional a uma variável Y. Quando , a distribuição de dado é definida por[26]
.
A definição acima não é válida se a distribuição de Y for absolutamente contínua dado que para todo . A definição seguinte é válida para quaisquer das duas variáveis aleatórias.
Definição[27] — Seja um par de variáveis aleatórias reais. Há uma distribuição de probabilidade , chamada de distribuição condicional de dado ou dado definida pela e para qualquer função limitada boreliana : quase certamente.
A distribuição também é denotada como ou . A igualdade anterior é uma igualdade entre variáveis aleatórias.[28]
Definição para σ-álgebra[editar | editar código-fonte]
De maneira mais geral, a distribuição de probabilidade é definida a partir da esperança condicional de uma variável aleatória dada uma σ-álgebra . Essa esperança condicional é a única variável aleatória -mensurável denotada como , satisfazendo para todo , variável -mensurável. Então, a distribuição condicional é definida por[29] , em que é a função indicadora.
Definição para distribuições absolutamente contínuas[editar | editar código-fonte]
No caso das distribuições absolutamente contínuas, existe uma função densidade condicional de uma distribuição em relação a outra e vice-versa. Se é a densidade da distribuição bidimensional, as duas densidades condicionais são dadas por[30]
e .
e são as duas distribuições marginais de e , respectivamente. Em substituição das integrais pelas somas, obtém-se fórmulas semelhantes quando as distribuições marginais são discretas ou quando a distribuição marginal de é discreta e de é absolutamente contínua ou vice-versa.[31]
Distribuição com valores em um espaço de Banach[editar | editar código-fonte]
Porque é um espaço de Banach, as distribuições dos valores em um espaço de Banach são generalizações das distribuições dos valores reais. A definição é semelhante.[32]
Definição — Sejauma variável aleatória em um espaço de probabilidade com valores em um espaço de Banach com σ-álgebra gerada pelos conjuntos abertos de . A distribuição de probabilidade da variável aleatória e a medida de probabilidade definida pelo espaço mensurável por para todo .
Para obter boas propriedades, é comum considerar as medidas de probabilidade tight. Isto é, Intuitivamente, são as medidas concentradas em seu espaço compacto e com a suposição que o espaço de Banach é separável.[33]
Um possível exemplo do espaço de Banach é o espaço das funções contínuas . Um processo estocástico de uma família de variáveis aleatórias indexadas por conjunto de índices . Uma definição possível da distribuição de probabilidade de tal processo é chamada de distribuição finita-dimensional.[34] Isto é, a distribuição multidimensional dos vetores quando . Então, a distribuição pode ser estendida pelo teorema da extensão de Carathéodory para todo o processo. Um exemplo é movimento browniano (trajetórias contínuas), cuja distribuição de probabilidade é a medida de Weiner[35] geralmente denotada por para todo subconjunto de .
Espaço de distribuições de probabilidade[editar | editar código-fonte]
Uma distribuição de probabilidade é uma medida de massa total unitária. O conjunto de distribuições de probabilidade é um subespaço do espaço de medidas finitas. Esse espaço é muitas vezes denominado[36] ou pelas distribuições de probabilidade reais. No restante da seção, as propriedades desse espaço são detalhadas para as distribuições de probabilidade no conjunto dos números reais. Embora também possam ser detalhadas para distribuições em espaços de Banach.
É possível fornecer esse espaço com uma topologia chamada topologia fraca.[36] Essa topologia define uma convergência fraca das distribuições de probabilidade: uma sequência de distribuições de probabilidade converge fracamente para uma distribuição de probabilidade se
para toda função contínua de um conjunto limitado.
A convergência é denominada .[36] Essa convergência é refletida pelo teorema de transferências de variáveis aleatórias das respectivas distribuições . Então, a convergência de variáveis aleatórias é chamada convergência em distribuição (ou fraca) é denotada ou . O termo convergência fraca das variáveis aleatórias é mais frequentemente utilizado.
O espaço de distribuições de probabilidade com topologia fraca é[37] um espaço métrico, completo e separável (no caso de um espaço de Banach também separável), tornando-se um espaço polonês.
Propriedades[editar | editar código-fonte]
Parâmetros e famílias[editar | editar código-fonte]
Certas distribuições são agrupadas por família em relação a certas propriedades da sua densidade ou da sua função massa de acordo com o número de parâmetros que as definem, chamados de família paramétrica de distribuição de probabilidade.[38]

Parâmetros[editar | editar código-fonte]
Os chamados parâmetros de posição[38] influenciam a tendência central da distribuição de probabilidade. Isto é, o valor ou os valores em torno dos quais a distribuição leva seus maiores valores como a esperança, a mediana, a moda, os quantils e os decils.
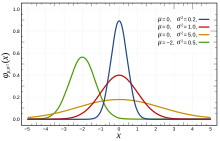
Os chamados parâmetros de escalonamento[38] influenciam a dispersão ou o achatamento da distribuição de probabilidade como a variância (momento de segunda ordem), o desvio padrão e o intervalo interquartil.
Os chamados parâmetros de forma[38] são outros parâmetros relacionados a distribuição de probabilidade. A cauda de uma distribuição de probabilidade real faz parte da sua forma. As caudas da esquerda e da direita são[39] dos tipos e , respectivamente. Uma distribuição de probabilidade é chamada de cauda pesada se a medida de probabilidade da cauda tende mais lentamente a 0, quando vai para infinito, do que a distribuição normal.[40] Especialmente para qualquer distribuição absolutamente contínua e centrada, adefinição pode ser representada em termos de densidade:[40]
é uma distribuição com caudas direita e esquerda pesadas.
A assimetria (momento de terceira ordem[41]) é um exemplo de parâmetro de forma, que permite tornar a cauda da direita mais ou menos pesada.[42] A curtose (momento de quarta ordem[41]) é usada para apoiar ou opor-se aos valores próximos da média daqueles que estão mais distantes. Uma distribuição de probabilidade é chamada de mesocúrtica, leptocúrtica ou platicúrtica se a curtose é 0, positiva ou negativa.
Famílias[editar | editar código-fonte]
Uma distribuição é chamada de família exponencial a um parâmetro[43] se sua densidade de probabilidade ou sua função massa depende de apenas uma parâmetro da seguinte forma:
Essa família inclui muitas distribuições clássicas como distribuição normal, distribuição exponencial, distribuição Gamma, distribuição qui-quadrado, distribuição beta, distribuição de Bernoulli, distribuição de Poisson, entre outras.
Uma distribuição é chamada de família potência a dois parâmetros[43] e se a densidade:
Distribuição direcional[editar | editar código-fonte]
Quando uma distribuição de probabilidade multidimensional representa a direção aleatória de um fenômeno, ela é chamada de direcional. É uma distribuição de um vetor aleatório unitário de dimensão , em que , ou, de maneira equivalente, é uma distribuição de probabilidade na esfera de dimensão . Uma distribuição direcional de dimensão d pode ser representada por um vetor (-1-dimensional) em coordenadas polares como as distribuições de von Mises e de Bingham.[44]
Momentos[editar | editar código-fonte]
Se existir, o -ésimo momento de uma distribuição de probabilidade é definido como . Essa fórmula é descrita[45] simplesmente como caso a distribuição seja definida a partir de uma variável aleatória .
O primeiro momento ou momento de ordem 1 também é chamado de esperança da distribuição. Quando o momento é igual a 0, a distribuição é chamada centrada. O segundo momento ou momento de ordem 2 também é chamado de variância da distribuição. Quando o momento é igual a 1, é dito que a distribuição é reduzida.
De uma maneira geral, a coleção de todos os momentos de uma distribuição de probabilidade não é suficiente para caracterizar essa distribuição.[46] Certas distribuições são definidas por um número finito do seu momento: a distribuição de Poisson é completamente definida por sua esperança,[47] a distribuição normal é completamente definida por seus dois primeiros momentos.[48] Certas distribuições não possuem momento como a distribuição de Cauchy.
Entropia[editar | editar código-fonte]
As distribuições de probabilidade permitem representar fenômenos aleatórios. A entropia de Shannon de uma distribuição de probabilidade foi introduzida em termodinâmica para quantificar a desordem molecular de um sistema.[49] O objetivo é medir a falta da informação em lei de probabilidade.[50] A entropia foi definida pela primeira vez para as distribuições discretas, tendo sido estendida para as distribuições absolutamente contínuas. Para uma distribuição discreta e uma distribuição de densidade , a entropia é definida respectivamente como[49][51]
e .
- A distribuição normal é a entropia máxima para todas as distribuições possíveis que possuem a mesma média e o mesmo desvio padrão.[9]
- A distribuição geométrica é a entropia máxima para todas as distribuições discretas que possuem a mesma média.[9]
- A distribuição uniforme contínua é a entropia máxima para as distribuições com suporte limitado.
- A distribuição exponencial é a entropia máxima para todas as distribuições em que possuem a mesma média.[9]
- As distribuições lei de potência como a lei de Zipf são a entropia máxima entre aqueles que tem a mesma média de logaritmo.
O estado de entropia máxima é o estado mais desordenado, mais estável e mais provável de um sistema.[50] Essas leis são os menos evitável de todas as leis compatíveis com as observações ou as condições. Portanto, a única forma objetiva de qualifica-las como distribuições de probabilidade a priori. Essa propriedade tem um papel importante na inferência bayeseana.
Classificação das distribuições de probabilidade na reta real[editar | editar código-fonte]

- em vermelho: distribuição absolutamente contínua (normal padrão);
- em azul: distribuição discreta (distribuição de Poisson de parâmetro 2);
- em preto: distribuição mista (combinação linear de uma medida de Dirac -2, uma medida de Dirac -1 e uma distribuição de Cauchy de parâmetros -2 e 1.
Distribuições de probabilidade em aplicações mais comuns são distribuições discretas e distribuições absolutamente contínuas. Entretanto, existem distribuições de probabilidade que não são nem discretas nem absolutamente contínuas.[47]
Distribuições discretas[editar | editar código-fonte]
Definição[editar | editar código-fonte]

Uma distribuição de probabilidade é concentrada[47] ou é realizada em um conjunto quando . Uma distribuição de probabilidade é chamada de discreta[11][12] se um conjunto é um conjunto finito ou contável.
O elemento é chamado de átomo de uma distribuição de probabilidade quando e . O conjunto de átomos de uma distribuição discreta é finito ou contável. De modo geral, essa propriedade é válida para toda medida -finita. Para uma distribuição de probabilidade real, o conjunto de átomos é exatamente o conjunto de pontos de descontinuidade de sua função de distribuição.[52] Neste caso, a finitude do conjunto de átomos é dada a partir do fato que a função de distribuição é limitada.[53]
Um critério suficiente para uma distribuição de probabilidade ser discreta é que seja finito ou contável.
Se é discreto, então ele se concentra em particular no conjunto (finito ou contável) dos seus átomos . Para definir é preciso definir o conjunto dos pares:[47] , em que é a função de massa de . Então, obtém-se
,
em que é a medida de Dirac[13][22] no ponto .
No caso em que a distribuição de probabilidade é definida a partir de uma variável aleatória, os conceitos anteriores são usados para a variável aleatória: uma variável aleatória , concentrada em conjunto , é discreta, se a distribuição concentrada em , é discreta. Os mesmo átomos de são os átomos de .[54]
Para uma variável aleatória discreta , o teorema de transferência é expresso na forma de somas ou de séries[54]
- , para toda função ,
- , para todo .
Geralmente a função de distribuição de uma distribuição discreta é constante seccionalmente.[47] Uma distribuição discreta pode ser representada por um gráfico de barras.[11]
Exemplos[editar | editar código-fonte]
Segue uma lista de distribuições de probabilidade discretas com suportes finitos ou contáveis.
- Medida de Dirac
A medida de Dirac é o exemplo mais simples das distribuições discretas no sentido que o suporte possui apenas um valor.[55] Se uma variável aleatória é a medida de Dirac , então é igual a com probabilidade igual a 1. Essa lei modela um fenômeno determinista (não aleatório) pois o resultado da experiência é quase certamente igual ao valor conhecido .
| Função de distribuição de probabilidade
da variável aleatória X |
Esperança
(1º momento) |
Variância
(2º momento) |
Notação |
|---|---|---|---|
| [56] |
- Distribuição uniforme discreta
A distribuição uniforme discreta modela um fenômeno aleatório cujos resultados são igualmente prováveis.[57] É o caso do lançamento de um dado. Se o suporte da distribuição é um conjunto de elementos , a distribuição é definida como
| Função de distribuição de probabilidade
da variável aleatória X |
Esperança
(1º momento) |
Variância
(2º momento) |
Notação |
|---|---|---|---|
| [57] |
- Distribuição de Bernoulli
A distribuição de Bernoulli corresponde a uma experiência com dois resultados (sucesso ou fracasso), que geralmente correspondem aos valores 1 e 0. Essa distribuição depende de um parâmetro para medir a probabilidade de sucesso, sendo definido por [58]
| Função de distribuição de probabilidade
da variável aleatória X |
Esperança
(1º momento) |
Variância
(2º momento) |
Notação |
|---|---|---|---|
| Ber(p) |
- Distribuição binomial
É a distribuição do número de sucessos obtidos depois de ensaios de Bernoulli independentes de parâmetros , ou seja, é a distribuição da soma de variáveis aleatórias independentes da distribuição de Bernoulli de mesmo parâmetro. Essa distribuição com suporte finito é definida por para todo .[58]
| Função de distribuição de probabilidade
da variável aleatória X |
Esperança
(1º momento) |
Variância
(2º momento) |
Notação |
|---|---|---|---|
| Bin(p,n) |
Distribuição aritmética
É uma distribuição que concentra-se em um conjunto do tipo , em que .[59]
Distribuição geométrica
É a distribuição que modela o tempo de espera do primeiro sucesso de uma de ensaios de Bernoulli independentes com probabilidade de sucesso . É a única distribuição discreta que possui a propriedade de falta de memória. Essa probabilidade com suporte infinito contável é definida por . para todo .
| Função de distribuição de probabilidade
da variável aleatória X |
Esperança
(1º momento) |
Variância
(2º momento) |
Notação |
|---|---|---|---|
| [60] |
Distribuição de Poisson
A distribuição de Poisson descreve o comportamento do número de eventos que ocorrem em um espaço determinado de tempo. Essa distribuição com suporte infinito contável depende de um parâmetro e é definida por para todo .
| Função de distribuição de probabilidade
da variável aleatória X |
Esperança
(1º momento) |
Variância
(2º momento) |
Notação |
|---|---|---|---|
| [60]183 | Poisson() |
Distribuição hipergeométrica
A distribuição hipergeométrica modela uma retirada simultânea de bolas uma urna contendo uma proporção de bolas vencedoras e uma proporção de bolas perdedoras para um número total de bolas. A distribuição descreve o número de bolas vencedoras extraídas. Essa distribuição com suporte finito depende de três parâmetros , e e é definida por
para todo .
Em geral fixamos a proporção, por exemplo .
| Função de distribuição de probabilidade
da variável aleatória X |
Esperança
(1º momento) |
Variância
(2º momento) |
Notação |
|---|---|---|---|
| [61] | [62] | [63] |
Distribuição absolutamente contínua[editar | editar código-fonte]
Definição[editar | editar código-fonte]
Uma distribuição de probabilidade real é chamada de absolutamente contínua[64] ou densidade[22] quando ela é absolutamente contínua em relação a medida de Lebesgue. Se é absolutamente contínua, então, de acordo com teorema de Radon-Nikodym,[65] ela possui uma densidade de probabilidade em relação a medida de Lebesgue. Isto é, existe[22] uma única (em relação a medida zero de Lebesgue) função mensurável positiva de tal modo que para qualquer : , em que é a função característica de Borel . Essa densidade de probabilidade nem sempre tem a expressão analítica (ver os exemplos abaixo).

Quando uma distribuição de probabilidade absolutamente contínua é definida a partir de uma variável aleatória , a variável aleatória é chamada absolutamente contínua[13] ou densidade e a densidade da distribuição é igualmente chamada densidade de , às vezes denotada .
Para uma variável aleatória absolutamente contínua , o teorema da transferência é escrita[66] por meio de uma integral de Lebesgue[64] para toda função integral em relação a medida :
A função de distribuição de uma distribuição absolutamente contínua é localmente absolutamente contínua, uma propriedade necessária e suficiente. Uma distribuição absolutamente contínua não possua átomos.[67] Entretanto, essa propriedade que opõe-se as distribuições absolutamente contínuas às distribuições discretas não é característica das distribuições absolutamente contínuas mas as leis contínuas (ver a seção distribuições singulares abaixo).
As distribuições absolutamente contínuas também são chamadas de distribuições contínuas.[68] Este é um equívoco, porque na maioria das aplicações Estatística as distribuições contínuas são absolutamente contínuas,[69] mas isso não é verdadeiro no caso geral.
Exemplos[editar | editar código-fonte]
- Distribuição uniforme
Intuitivamente uma distribuição uniforme sobre um intervalo indica que todos os valores do intervalo tem a mesma chance de aparecer. Mais formalmente cada subintervalo tem uma probabilidade igual a medida de Lebesgue de (multiplicado por uma constante). A distribuição uniforme depende apenas do intervalo, o seu suporte é compacto e a sua densidade é dada pela:
- para .
- em caso contrário.[70]
| Distribuição de probabilidade
da variável aleatória X (densidade) |
Esperança
(1º momento) |
Variância
(2º momento) |
Notação |
|---|---|---|---|
| [70] |
- Distribuição exponencial
A distribuição exponencial é comumente usada para modelar o tempo de vida de um fenômeno pois é a única distribuição absolutamente contínua com propriedade de falta de memória. Ela pode ser considerada como um análogo continuo de distribuição geométrica. Essa distribuição com suporte semi-infinito depende de um parâmetro (às vezes chamado de intensidade), em que a densidade é definida como para todo .[71]
| Distribuição de probabilidade
da variável aleatória X (densidade) |
Esperança
(1º momento) |
Variância
(2º momento) |
Notação |
|---|---|---|---|
| [71] |
Distribuição normal
Uma distribuição normal ou distribuição gaussiana é uma distribuição central na teoria da probabilidade. Ela descreve o comportamento de séries de experiências aleatórias quando o número de tentativas é muito grande. É a distribuição limite do teorema central do limite. Ela é igualmente a única distribuição estável de parâmetro 2. A distribuição normal é caracterizada por sua média (que também é sua mediana) e seu desvio-padrão, com suporte da toda reta real. Sua densidade é simétrica e sua forma é comumente chamada de curva de Gauss ou curva em sino.[72]
| Distribuição de probabilidade
da variável aleatória X (densidade) |
Esperança
(1º momento) |
Variância
(2º momento) |
Notação |
|---|---|---|---|
| [72] |
- Distribuição de Cauchy
A distribuição de Cauchy é a distribuição estável de parâmetro 1, o que dá as boas propriedades. Entretanto, é um exemplo típico de distribuição que não admite momentos, em particular nem média nem variância. Com suporte da toda reta real a sua densidade é simétrica.[73]
| Distribuição de probabilidade
da variável aleatória X (densidade) |
Esperança
(1º momento) |
Variância
(2º momento) |
|---|---|---|
| Não existe (é infinita) [73] | Não existe (é infinita) [73] |
A distribuição da posição de um movimento browniano no plano quando se atinge a reta é uma distribuição de Cauchy.[74]
Distribuição de Tukey-Lambda
Uma distribuição de Tukey-Lamba é uma distribuição absolutamente contínua. Logo possui uma densidade de probabilidade, mas não possui uma expressão analítica. Essa distribuição depende de um parâmetro e é definida a partir da função quantil .[75]
Distribuições singulares[editar | editar código-fonte]
Definição[editar | editar código-fonte]
Uma distribuição de probabilidade é chamada de contínua ou difusa[52] quando não possui nenhum átomo.
Em particular, as distribuições absolutamente contínuas são contínuas mesmo que o inverso não seja verdadeiro. A função de distribuição de uma distribuição contínua ser contínua[52] é uma propriedade necessária e suficiente.
Uma distribuição de probabilidade é chamada de singular quanto ela é contínua, mas não absolutamente contínua. Isto é, quando uma distribuição singular não possui nem átomo nem densidade. Esses conceitos também valem para as distribuições de probabilidade definidas a partir de variáveis aleatórias: uma variável aleatória é contínua ou difusa, respectivamente singular, quando a distribuição de probabilidade associada é contínua ou difusa, respectivamente singular.[52]
Exemplo[editar | editar código-fonte]

Distribuição de Cantor
É uma distribuição singular, definida a partir do conjunto de Cantor . Quando são variáveis aleatórias independentes e identicamente distribuídas de uma distribuição uniforme discreta em , então é uma variável aleatória da distribuição de Cantor.[76] Essa distribuição de probabilidade[77] descrita como é a distribuição uniforme do conjunto de Cantor. Sua função de distribuição é a escada de Cantor, diferenciável quase em todos pontos e derivada igual a zero em quase todos pontos.[76]
Em aplicações, é raro que uma distribuição contínua contenha uma parte singular.[69] Entretanto, o conjunto de Cantor aparece em exemplos conhecidos como o conjunto de zeros do movimento browniano.
Outros casos[editar | editar código-fonte]
Existem distribuições de probabilidade que não são nem discretas nem absolutamente contínuas nem singulares, às vezes denominadas leis mistas.[78][79] De um ponto de vista mais geral, toda distribuição de probabilidade pode se decompor[69][53] em uma combinação linear de uma distribuição contínua e de uma distribuição discreta . O teorema da decomposição de Lebesgue aplicado[69] a indica que essa distribuição contínua se decompõe em uma combinação linear de duas distribuições contínua, uma absolutamente contínua com relação à medida de Lebesgue e outra singular sem relação à medida de Lebesgue. Então, a decomposição é descrita como , em que e . A presença de garante que .
A seguinte distribuição de probabilidade real de um exemplo de uma distribuição mista obtida com a junção entre a distribuição discreta definida pelos átomos com a função de massa , e a distribuição absolutamente contínua[69] de densidade é descrita como sendo . Sua função de distribuição é uma função contínua por partes,[80] mas não constante por partes como as funções de distribuição das distribuições discretas.
Intuitivamente isso corresponde a um fenômenos aleatório com a distribuição absolutamente contínua. Imagine o aparelho de medida que não pode medir os dados a partir de um certo limiar . Todas as medidas não detectadas pelo aparelho serão atribuídas a 0: a distribuição será nula em qualquer parte menor do que , em seguida, um salto aparece em singleton . As medidas seguem a distribuição absolutamente contínua para os valores maiores que .[78] No exemplo, a função de distribuição é descontínua em .
Características de uma distribuição de probabilidade[editar | editar código-fonte]
Existem várias funções de variáveis reais ou complexas que determinam exclusivamente as distribuições de probabilidade. Certas propriedades dessas funções permitem deduzir propriedades para as distribuições como o cálculo de momento ou uma expressão da convergência em distribuição.[2]
Utilização da função de distribuição[editar | editar código-fonte]

De acordo com o sistema de Dynkin, os conjuntos chamados paralelepípedos ou retângulos geram[81] algebra de Borel que são suficientes para definir uma distribuição de probabilidade dos paralelepípedos. Supõe-se que a distribuição de probabilidade seja real. Isto é, .
A função de distribuição de uma distribuição de probabilidade real denotada como [82] é a função definida para todo
Uma distribuição de probabilidade é caracterizada por sua função de distribuição. Isto é, duas distribuições de probabilidade são iguais se e somente se suas funções de distribuição forem iguais.[83]
Mais genericamente, toda função monótona càdlàg é verificável: e são funções de distribuição de uma única[84] distribuição de probabilidade em . A distribuição de probabilidade definida a partir de uma função de distribuição é chamada de medida de Lebesgue-Stieltjes.[83]
Uma das vantagens da função é que ela é bem definida para qualquer distribuição de probabilidade.[84] Entretanto, ela nem sempre tem expressão explícita, por exemplo, a função de distribuição de distribuição normal. A função de distribuição às vezes permite o cálculo de distribuições tais que como a distribuição do máximo ou do mínimo de uma amostra e fornece um critério conveniente[85] de convergência de distribuições de probabilidade pelo teorema de Portmanteau.
Utilização da função característica[editar | editar código-fonte]

Chamada função característica de uma distribuição de probabilidade e denotada como é a simetria da transformada de Fourier de . Para todo :
Como o nome sugere, a função característica determina exclusivamente a distribuição.[86] Isto é, duas distribuições de probabilidade são iguais se e somente se suas funções características forem iguais.
Uma das vantagens da distribuição característica é que ela existe para toda distribuição de probabilidade.[87][85] Usando a fórmula da inversão da transformada de Fourier,[88] a distribuição de probabilidade também é obtida a partir da função característica. A representação das distribuições para as funções características ainda permite caracterizar[89] a convergência das distribuições de probabilidade pelo teorema de Portmanteau.
Nos casos em que a distribuição de probabilidade é definida a partir de uma variável aleatória , de acordo com o teorema da transferência para todo
Utilização da função geradora de momentos[editar | editar código-fonte]
A função geradora de momentos de uma distribuição de probabilidade denotada como é a simetria da transformada de Laplace[90][77] de . Quando a função é integrada em relação à medida para todo :
A função geradora de momentos determina a distribuição de probabilidade unicamente se essa função existe em um intervalo que contem a origem.[91]
Uma das vantagens da função geradora de momentos é que ela permite encontrar os momentos da distribuições de probabilidade pelas derivadas.[90] Para todo , a -ésima derivada da função geradora de momento em 0 é o momento da distribuição de probabilidade em que .
A representação das distribuições para a função geradora de momentos também permite caracterizar[91] a convergência das distribuições de probabilidade pelo teorema de Portmanteau.
Nos casos em que a distribuição de probabilidade é definida a partir de uma variável aleatória , de acordo com o teorema da transferência para todo : .
Para as distribuições definidas a partir de variáveis aleatórias, essa função também permite mostrar a independência das variáveis.[90]
Existe um caso particular das distribuições discretas. A função geradora de probabilidades de uma distribuição de probabilidade discreta é definida[90] como a esperança da série geradora sub a condição da existência desta série. Essa função geradora determina a distribuição de probabilidade unicamente.[90]
Outras características[editar | editar código-fonte]
A função quantil[92] de uma distribuição de probabilidade real denotada como é a função que fornece o quantil da distribuição. Ela é definida como para[93] todo : , em que é a função de distribuição de .

Certas distribuições de probabilidade são mais fáceis de definir pela função quantil. Intuitivamente é o valor tal que uma proporção de valores possíveis menor de que esse valor é igual . , , e são, respectivamente, o primeiro quantil, a mediana e o terceiro quantil da distribuição.
Se é bicontínua[94] então é a função recíproca da função de distribuição[94] , sendo que no caso geral também é chamada de função quantil recíproca geradora de ou função inversa contínua à direita de .
Essa função quantil determina a distribuição associada[93] a no sentido que, se é uma variável aleatória da distribuição uniforme contínua de , então é uma variável aleatória da distribuição inicial . Essa representação é particularmente útil por simular as distribuições de probabilidade,[95] sendo suficiente então para simular uma distribuição uniforme contínua e aplicar a função quantil (ver seção abaixo sobre simulação de distribuição de probabilidade).
Certas distribuições não são funções de distribuição explícitas, mas são definidas a partir de uma função quantil é um caso da distribuição de Tukey-Lambda.
Utilizações[editar | editar código-fonte]
Frequentemente a distribuição estatística de uma variável em uma população refere-se aos modelos matemáticos da distribuição de probabilidade.[96] Geralmente é interessante estudar o modelo probabilístico por razões práticas e teóricas, de acordo com afirmações acadêmicas.[97] O estudo começa com uma seleção aleatória de diversos valores ou indivíduos. Se o método utilizado for perfeito (se os valores observados são derivados de uma seleção equiprovável),[96] então são variáveis aleatórias e o estudo do fenômeno equivale ao estudo da distribuição de probabilidade.
Simulação de uma distribuição de probabilidade[editar | editar código-fonte]
Para estudar as distribuições de probabilidade, é importante fazer simulações. Em particular, com o uso de computadores. As distribuições de probabilidade são caracterizadas pela função quantil por meio de uma variável aleatória com distribuição uniforme. Em geral, esse método engloba duas etapas:[98] gerar os referidos valores pseudo aleatórios com distribuição uniforme e inverter a função de distribuição da distribuição estudada. Como a segunda etapa não é óbvia para todas as distribuições, outros métodos são utilizados.
| “ | Qualquer um que considere métodos aritméticos para produzir dígitos está certamente cometendo um pecado. | ” |

Simulação da distribuição uniforme[editar | editar código-fonte]
Para obter valores da distribuição uniforme contínua, o computador simula os valores da distribuição uniforme discreta. Podem ser usados vários métodos:[99] os algoritmos aritméticos são o método mais simples, enquanto que as tabelas que podem conter mais de um milhão de dados são cada vez menos utilizadas e os processos físicos como a criação de um ruído de fundo são bastante onerosos para a recuperação de dados. Como os algoritmos são deterministas (não aleatórios), os valores obtidos são chamados pseudo aleatórios. Muitos algoritmos foram desenvolvidos para melhorar a independência e a distribuição entre os valores no intervalo .
- Simulação das outras distribuições
Quando a função de distribuição é reversível, usa-se a caracterização pela função quantil. Quando a função de distribuição não é reversível, podem ser usados os seguintes métodos: a transformação de Box-Muller simula a distribuição normal,[100] a técnica de rejeição de von Neumann é baseada em um teste estatístico e é aplicável a várias distribuições,[101] dentre outros métodos específicos.[102]
- Exemplo
Um exemplo conhecido de utilização de uma simulação de distribuição de probabilidade é o método de Monte Carlo. Por exemplo, para aproximar o valor de . O método de Monte Carlos consiste em simular um grande número de valores de acordo com uma distribuição uniforme contínua em e computar a proporção dos pares em que . Essa proporção aproxima-se de quando o número de pontos tende ao infinito.[103]
Aproximação de uma distribuição de probabilidade[editar | editar código-fonte]
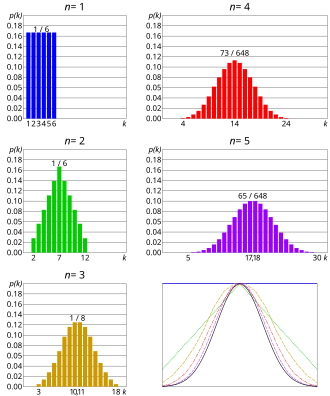
Várias aproximações de uma distribuição de probabilidade existem usando diferentes métodos descritos acima. Essas são as técnicas usadas geralmente em casos práticos. O primeiro passo é o recolhimento dos dados, que permite construir objetos empíricos como a função de distribuição empírica. Esses objetos empíricos são às vezes chamados de distribuição de probabilidade, mas são realmente leis empíricas chamadas de distribuições estatísticas.[96] Os teoremas limites ou os testes estatísticos permitem finalmente identificar a melhor distribuição de probabilidade que modela o fenômeno aleatório inicial.[97]
| “ | As probabilidades devem ser consideradas análogas às medidas das grandezas físicas, ou seja, nunca podem ser conhecidas com exatidão, mas apenas podem ser conhecidas com certa aproximação.[104] | ” |
Função de distribuição[editar | editar código-fonte]
O teste estatístico de Kolmogorov-Smirnov, baseado no teorema de Portmanteau, permite identificar a função de distribuição empírica calculada a partir dos dados de uma função de distribuição de uma distribuição de probabilidade, em função de uma taxa de rejeição. A vantagem da convergência das funções de distribuição é que as funções existem para todas as distribuições de probabilidade. Essa convergência permite particularmente aproximar uma distribuição absoluta contínua de uma série de distribuições discretas.[105]
Convergência de outras funções características[editar | editar código-fonte]
Diferentes teoremas de convergência de variáveis aleatórias permitem construir uma sequência de distribuições de probabilidade que converge para uma determinada distribuição ou uma distribuição como o limite das distribuições de probabilidade. O teorema central do limite coloca a distribuição normal como a distribuição limite. O teorema da continuidade de Paul Lévy refere-se a convergência das funções características.[105]

Regressão quantílica[editar | editar código-fonte]
A regressão quantílica permite aproximar os quantis da distribuição dos quantis empíricos. Isto é, calculados a partir de quaisquer dados. Um teste estatístico pode ser usado para comparar os quantis empíricos (observados) com os quantis da suposta distribuição para modelar o fenômeno estudado. Essa abordagem é particularmente útil por estudar certas distribuições que não são explicitamente conhecidas por sua função densidade ou sua função de distribuição, mas por seus quantis como a distribuição de Tukey-Lambda.[105]
Testes estatísticos[editar | editar código-fonte]
Vários testes estatísticos existem para comparar duas distribuições. Especificamente, os testes de aderência permitem comparar uma distribuição empírica (isto é, calcular a partir de dados baseados em amostras) com uma suposta distribuição de probabilidade para modelar o fenômeno estudado. Os dois principais testes estatísticos são o teste de Kolmogorov-Smirnov que compara as funções de distribuição e o teste de adequação qui-quadrado que compara os efeitos observados com a distribuição qui-quadrado. Os testes com distribuição normal são chamados testes de normalidade.[106]
Os testes de homogeneidade permitem comparar duas distribuições empíricas para verificar se elas pertencem ao mesmo fenômenos ou se elas podem ser modeladas pela mesma distribuição de probabilidade a priori. Esses testes comparam certas propriedades das distribuições empíricas com as propriedades da distribuição a priori. Eles são úteis na prática porque permite comparar não as distribuições inteiras, mas os valores das distribuições:[107] o teste de Fisher estima as variâncias empíricas por meio da distribuição de Fisher,[107] o teste de Student estima a média empírica por meio da distribuição de Student,[108] etc..
Exemplos de modelagem[editar | editar código-fonte]
As distribuições de probabilidade são usadas para representar os fenômenos observados. Uma distribuição de probabilidade é dita a priori se ela é assumida para modelar os dados recuperados. Os testes estatísticos são realizados para afirmar ou rejeitar a concordância da distribuição de probabilidade com os dados. Em muitas áreas, os métodos evoluíram e melhores distribuições de probabilidade foram criadas para atender os problemas. Segue uma lista com exemplos concretos de modelagem:
- na economia: a bolsa de valores é uma instituição de troca de bens e de títulos mobiliários. É realizado um estudo da evolução histórica dos preços, incluindo a modelagem da variação dos preços, para melhor estimar os preços futuros de um bem ou de um título. Essas variações foram modeladas por uma distribuição normal em um primeiro momento e melhoradas com distribuições de Pareto estáveis em um segundo momento. Esses novos modelos sempre procuraram melhorar a percepção de risco desde então.[106]
- em jogos de azar: para jogar na loteria francesa, é possível escolher 6 entre 49 números possíveis. Se os números são escolhidos ao acaso pelos apostadores (isto é, com uma distribuição uniforme discreta), então o número de ganhadores segue uma distribuição de Poisson. Um estudo pode ser realizado porque o número de ganhadores é um dado conhecido. Parece que a escolha não é uniforme, mas que alguns números foram escolhidos mais do que outros.[109]
- em manutenção: uma boa compreensão da degradação permite melhorar a performance da manutenção. Várias distribuições a priori são usadas para modelar a evolução das fissuras das calçadas: a distribuição exponencial, a distribuição de Weibull, a distribuição log-normal, a distribuição log-logística etc . Para a utilização do método da máxima verossimilhança, a distribuição log-logística faz parte das distribuições mais adequadas.[110]
- em medicina: para testar a eficácia dos medicamentos, um ensaio clínico é realizado com uma amostra de pacientes. Esse método faz parte da teoria da decisão. Ele consiste em selecionar um paciente para realizar um teste com dois resultados possíveis (sucesso ou fracasso). Isto é, um teste modelado por uma distribuição de Bernoulli. Em seguida, o teste é repetido quantas vezes forem necessárias. Esse é o método de ensaio de Bernoulli. Um método melhor é usar a distribuição hipergeométrica, que permite considerar apenas o conjunto de pacientes previamente definido.[111]
- em meteorologia: em hidrologia, a pluviometria é o estudo da quantidade de água depois de uma chuva em um ponto do solo por um determinado período de tempo. Não há consenso entre a comunidade científica internacional sobre a escolha da distribuição a priori. Uns autores defendem o uso da distribuição log-normal que se ajusta bem aos valores pequenos. Outros autores sugerem o uso da distribuição gama que se ajusta bem aos valores experimentais. O uso da distribuição de Pareto é interessante para representar os valores médios.[112]
Ver também[editar | editar código-fonte]
- Axiomas de probabilidade
- Medida
- Probabilidade
- Probabilidade condicionada
- Teoria das probabilidades
- Variável aleatória
Referências
- ↑ a b c Wackerly, Dennis; Mendenhall, William; Schaeffer, Richard L. (2008). Mathematical Statistics with Applications. Belmont: Brooks Cole. 86 páginas
- ↑ a b c Barbé, Philippe; Ledoux, Michel (2007). Probabilité. Les Ulis: EDP Sciences. 229 páginas
- ↑ a b Henry, Michel (2001). Probabilités et Statistique. Besançon: Presses Universitaires de Franche-Comté. 14 páginas
- ↑ Dalang, Robert C.; Conus, Daniel (2008). Introduction à la Théorie des Probabilités. [S.l.]: Presses Polytechniques et Universitaires Romandes. 127 páginas
- ↑ Henry, Michel (2001). Probabilités et Statistique (Besançon: Presses Universitaires de Franche-Comté). p. 34
- ↑ a b c d Dalang, Robert C.; Conus, Daniel (2008). Introduction à la Théorie des Probabilités. [S.l.]: Presses Polytechniques et Universitaires Romandes. 128 páginas
- ↑ Henry, Michael (2001). Probabilités et Statistique. Besançon: Presses Universitaires de Franche-Comté. 42 páginas
- ↑ Henry, Michael (2001). Probabilités et Statistique. Besançon: Presses Universitaires de Franche-Comté. 54 páginas
- ↑ a b c d Caumel, Yves (2011). Probabilités et Processus Stochastiques. Paris: Springer. 137 páginas
- ↑ Henry, Michael (2001). Probabilités et Statistique. Besançon: Presses Universitaires de Franche-Comté. 55 páginas
- ↑ a b c Ruegg, Alan (1994). Autour de la Modélisation en Probabilités. [S.l.]: Presses Polytechniques et Universitaires Romandes. 35 páginas
- ↑ a b Saporta, Gilbert (2006). Probabilités, Analyse des Données et Statistiques. Paris: Éditions Technip. 16 páginas
- ↑ a b c Barbé, Philippe; Ledoux, Michel (2007). Probabilité. Les Ulis: EDP Sciences. 45 páginas
- ↑ Ducel, Yves (1996). Les Probabilités à L'agrégation Externe de Mathématiques: Guide pour une Révision. Besançon: Presses Universitaires de Franche-Comté. 8 páginas
- ↑ Barbé, Philippe; Ledoux, Michel (2007). Probabilité. Les Ulis: EDP Sciences. 54 páginas
- ↑ Shiryaev, Albert (1995). Probability. Nova Iorque: Springer - Verlag. 196 páginas
- ↑ Shiryaev, Albert (1995). Probability. Nova Iorque: Springer - Verlag. 160 páginas
- ↑ Saporta, Gilbert (2006). Probabilités, Analyse des Données et Statistiques. Paris: Éditions Technip. 69 páginas
- ↑ Saporta, Gilbert (2006). Probabilités, Analyse des Données et Statistiques. Paris: Éditions Technip. 22 páginas
- ↑ Saporta, Gilbert (2006). Probabilités, Analyse des Données et Statistiques. Paris: Éditions Technip. 85 páginas
- ↑ Saporta, Gilbert (2006). Probabilités, Analyse des Données et Statistiques. Paris: Éditions Technip. 87 páginas
- ↑ a b c d Ducel, Yves (1996). Les Probabilités à L'agrégation Externe de Mathématiques: Guide pour une Révision. Besançon: Presses Universitaires de Franche-Comté. 9 páginas
- ↑ a b Barbé, Philippe; Ledoux, Michel (2007). Probabilité. Les Ulis: EDP Sciences. 51 páginas
- ↑ Ruegg, Alan (1994). Autour de la Modélisation en Probabilités. [S.l.]: Presses Polytechniques et Universitaires Romandes. 20 páginas
- ↑ Klebaner, Fima (2005). Introduction to Stochastic Calculus With Applications. Londres: Imperial College Press. 44 páginas
- ↑ a b Barbé, Philippe; Ledoux, Michel (2007). Probabilité. Les Ulis: EDP Sciences. 150 páginas
- ↑ Barbé, Philippe; Ledoux, Michel (2007). Probabilité. Les Ulis: EDP Sciences. 162 páginas
- ↑ Barbé, Philippe; Ledoux, Michel (2007). Probabilité. Les Ulis: EDP Sciences. 160 páginas
- ↑ Klebaner, Fima (2005). Introduction to Stochastic Calculus With Applications. Londres: Imperial College Press. 46 páginas
- ↑ Saporta, Gilbert (2006). Probabilités. Paris: Éditions Technip. 77 páginas
- ↑ Saporta, Gilbert (2006). Probabilités. Paris: Éditions Technip. 80 páginas
- ↑ Ledoux, Michel; Talagrand, Michel (2002). Probability in Banach Spaces. Berlin: Springer. 37 páginas
- ↑ Ledoux, Michel; Talagrand, Michel (2002). Probability in Banach Spaces. Berlin: Springer. 38 páginas
- ↑ Shiryaev, Albert (1995). Probability. Nova Iorque: Springer - Verlag. 178 páginas
- ↑ Klebaner, Fima (2005). Introduction to Stochastic Calculus With Applications. Londres: Imperial College Press. 139 páginas
- ↑ a b c Ledoux, Michel; Talagrand, Michel (2002). Probability in Banach Spaces. Berlin: Springer. 39 páginas
- ↑ Ledoux, Michel; Talagrand, Michel (2002). Probability in Banach Spaces. Berlin: Springer. 40 páginas
- ↑ a b c d Ruppert, David (2004). Statistics and Finance: An Introduction. Ithaca: Springer. 17 páginas
- ↑ Ruppert, David (2004). Statistics and Finance: An Introduction. Ithaca: Springer. 25 páginas
- ↑ a b Ruppert, David (2004). Statistics and Finance: An Introduction. Ithaca: Springer. 30 páginas
- ↑ a b Ruppert, David (2004). Statistics and Finance: An Introduction. Ithaca: Springer. 26 páginas
- ↑ Ruppert, David (2004). Statistics and Finance: An Introduction. Ithaca: Springer. 24 páginas
- ↑ a b Wackerly, Dennis; Mendenhall, William; Schaeffer, Richard L. (2008). Mathematical Statistics with Applications. Belmont: Brooks Cole. 463 páginas
- ↑ Mardia, K. V. «Characterizations of Directional Distributions». Statistical Distributions in Scientific Work: 365 - 385
- ↑ Shiryaev, Albert (1995). Probability. Nova Iorque: Springer. 182 páginas
- ↑ Shiryaev, Albert (1995). Probability. Nova Iorque: Springer. 294 páginas
- ↑ a b c d e Shiryaev, Albert (1995). Probability. Nova Iorque: Springer. 155 páginas
- ↑ Shiryaev, Albert (1995). Probability. Nova Iorque: Springer. 234 páginas
- ↑ a b Caumel, Yves (2011). Probabilités et Processus Stochastiques. Paris: Springer. 135 páginas
- ↑ a b Jedrzejewski, Franck (2009). Modèles Aléatoires et Physique Probabiliste. Paris: Springer. 13 páginas
- ↑ Caumel, Yves (2011). Probabilités et Processus Stochastiques. Paris: Springer. 136 páginas
- ↑ a b c d Martiano, Jean-Jacques (2006). Maths: Prépas Commerciales. [S.l.]: Sutdyrama. 242 páginas
- ↑ a b Barbé, Philippe; Ledoux, Michel (2007). Probabilité. Les Ulis: EDP Sciences. 47 páginas
- ↑ a b Martiano, Jean-Jacques (2006). Maths: Prépas Commerciales. [S.l.]: Studyrama. 157 páginas
- ↑ Barbé, Philippe (2007). Probabilité. Les Ulis:: EDP Sciences. 13 páginas
- ↑ «Análise Multivariada». Universidade Estadual de Campinas (UNICAMP). 4 páginas. Consultado em 23 de novembro de 2016
- ↑ a b Farias, Ana Maria Lima de. «Variáveis Aleatórias Discretas» (PDF). Universidade Federal Fluminense (UFF). 31 páginas. Consultado em 23 de novembro de 2016. Arquivado do original (PDF) em 27 de março de 2016
- ↑ a b Peternelli, Luiz Alexandre (1 de março de 2004). «Algumas distribuições de variáveis aleatórias discretas e contínuas» (PDF). "Estatística I". UFV. p. 68-82. Consultado em 29 de novembro de 2016
- ↑ «Arithmetic distribution - Encyclopedia of Mathematics». www.encyclopediaofmath.org. Consultado em 30 de novembro de 2016
- ↑ a b Ross, Sheldon (2010). Probabilidade - Um Curso Moderno com Aplicações. Porto Alegre: Bookman. pp. 195 – 197
- ↑ Ross, Sheldon (2010). Probabilidade - Um Curso Moderno com Aplicações. Porto Alegre: Bookman. 200 páginas
- ↑ Ross, Sheldon (2010). Probabilidade - Um Curso Moderno com Aplicações. Porto Alegre: Bookman. 203 páginas
- ↑ Ross, Sheldon (2010). Probabilidade - Um Curso Moderno com Aplicações. Porto Alegre: Bookman. 204 páginas
- ↑ a b Shiryaev, Albert (1995). Probability. Nova Iorque: Springer. 156 páginas
- ↑ Barbé, Philippe; Ledoux, Michel (2007). Probabilité. Les Ulis: EDP Sciences. 31 páginas
- ↑ Barbé, Philippe; Ledoux, Michel (2007). Probabilité. Les Ulis: EDP Sciences. 42 páginas
- ↑ Ruegg, Alan (1994). Autour de la Modélisation en Probabilités. [S.l.]: Presses Polytechniques et Universitaires Romandes. 52 páginas
- ↑ Saporta, Gilbert (2006). Probabilités. Paris: Éditions Technip. 18 páginas
- ↑ a b c d e Klebaner, Fima (2005). Introduction to Stochastic Calculus With Applications. Londres: Imperial College Press. 36 páginas
- ↑ a b BUSSAB & MORETTIN (2002), p. 173
- ↑ a b BUSSAB & MORETTIN (2002), p. 180
- ↑ a b BUSSAB & MORETTIN (2002), p. 175
- ↑ a b c CASELLA & BERGER (2010), p. 97.
- ↑ Michel Balazard; Éric Saiar; Marc Yor. «Note sur la Fonction Zeta de Riemann, 2» (PDF). Advances in Mathematics: 284 - 287
- ↑ Corlu, Canan G.; Melike. «Estimating the Parameters of the Generalized Lambda Distribution: Which Method Performs Best?». Communications in Statistics - Simulation and Computation. 45 (7): 2276–2296. doi:10.1080/03610918.2014.901355
- ↑ a b Klebaner, Fima (2005). Introduction to Stochastic Calculus With Applications. Londres: Imperial College Press. 37 páginas
- ↑ a b Ledoux, Michel; Talagrand, Michel (2002). Probability in Banach Spaces. Berlin: Springer. 22 páginas
- ↑ a b Bogaert, Patrick (2006). Probabilités pour Scientifiques et Ingénieurs. Paris: Éditions De Boeck. 71 páginas
- ↑ Caumel, Yves (2011). Probabilités et Processus Stochastiques. Paris: Springer. 80 páginas
- ↑ Bogaert, Patrick (2006). Probabilités pour Scientifiques et Ingénieurs. Paris: Éditions De Boeck. 72 páginas
- ↑ Shiryaev, Albert (1995). Probability. Nova Iorque: Springer. 144 páginas
- ↑ Shiryaev, Albert (1995). Probability. Nova Iorque: Springer. 151 páginas
- ↑ a b Shiryaev, Albert (1995). Probability. Nova Iorque: Springer. 154 páginas
- ↑ a b Shiryaev, Albert (1995). Probability. Nova Iorque: Springer. 152 páginas
- ↑ a b Klebaner, Fima (2005). Introduction to Stochastic Calculus With Applications. Londres: Imperial College Press. 38 páginas
- ↑ Shiryaev, Albert (1995). Probability. Nova Iorque: Springer. 282 páginas
- ↑ Saporta, Gilbert (2006). Probabilités. Paris: Éditions Technip. 55 páginas
- ↑ Saporta, Gilbert (2006). Probabilités. Paris: Éditions Technip. 57 páginas
- ↑ Shiryaev, Albert (1995). Probability. Nova Iorque: Springer. 322 páginas
- ↑ a b c d e Saporta, Gilbert (2006). Probabilités. Paris: Éditions Technip. 60 páginas
- ↑ a b Klebaner, Fima (2005). Introduction to Stochastic Calculus With Applications. Londres: Imperial College Press. 38 páginas
- ↑ Bogaert, Patrick (2006). Probabilités pour Scientifiques et Ingénieurs. Paris: Éditions De Boeck. 88 páginas
- ↑ a b Barbé, Philippe; Ledoux, Michel (2007). Probabilité. Les Ulis: EDP Sciences. 50 páginas
- ↑ a b Bogaert, Patrick (2006). Probabilités pour Scientifiques et Ingénieurs. Paris: Éditions De Boeck. 88 páginas
- ↑ Barbé, Philippe; Ledoux, Michel (2007). Probabilité. Les Ulis: EDP Sciences. 49 páginas
- ↑ a b c Saporta, Gilbert (2006). Probabilités, Analyse des données et Statistiques. Paris: Éditions Technip. 28 páginas
- ↑ a b Ruegg, Alan (1994). Autour de la Modélisation en Probabilités. [S.l.]: Presses Polytechniques et Universitaires Romandes. 37 páginas
- ↑ Jedrzejewski, Franck (2009). Modèles Aléatoires et Physique Probabiliste. [S.l.]: Springer. 187 páginas
- ↑ Jedrzejewski, Franck (2009). Modèles Aléatoires et Physique Probabiliste. [S.l.]: Springer. 182 páginas
- ↑ Jedrzejewski, Franck (2009). Modèles Aléatoires et Physique Probabiliste. [S.l.]: Springer. 188 páginas
- ↑ Jedrzejewski, Franck (2009). Modèles Aléatoires et Physique Probabiliste. [S.l.]: Springer. 189 páginas
- ↑ Jedrzejewski, Franck (2009). Modèles Aléatoires et Physique Probabiliste. [S.l.]: Springer. 191 páginas
- ↑ Jedrzejewski, Franck (2009). Modèles Aléatoires et Physique Probabiliste. [S.l.]: Springer. 215 páginas
- ↑ Henry, Michel (2001). Probabilités et Statistique (Besançon: Presses Universitaires de Franche-Comté). p. 194
- ↑ a b c Bogaert, Patrick (2006). Probabilités pour Scientifiques et Ingénieurs. Paris: Éditions De Boeck. 70 páginas
- ↑ a b Albouy, Michel; A. Sinani (1981). «L'efficience des Bourses de Province Françaises» (PDF). Journal de la Société Statistique de Paris: 200 - 214
- ↑ a b Saporta, Gilbert (2006). Probabilités, Analyse des données et Statistiques. Paris: Éditions Technip. 340 páginas
- ↑ Saporta, Gilbert (2006). Probabilités, Analyse des données et Statistiques. Paris: Éditions Technip. 342 páginas
- ↑ Roger, P.; M.-H. Broihanne (2006). «Les Joueurs de Loto Français Choisissent-Ils leurs Numéros au Hasard?» (PDF). Revue de Statistique Appliquée: 83 - 98. Consultado em 9 de novembro de 2016
- ↑ Courilleau, E. Courilleau; J. M. Marion (1999). «Comparaison de Modèles D'Estimation de la Fonction de Survie Appliquée à des Données Routières» (PDF). Revue de Statistique Appliquée: 81- 97. Consultado em 9 de novembro de 2016
- ↑ Boutros-Toni, F. (1981). «L'Analyse Séquentielle Exhaustive. Application en Médecine» (PDF). Revue de Statistique Appliquée: 31 - 50. Consultado em 9 de novembro de 2016
- ↑ Reffye, J. de (1982). «Étude Phénoménologique des Précipitations Pluvieuses. Modélisation Mathématiques des Intensités de Pluie en un Point du Sol» (PDF). Revue de Statistique Appliquée: 39 - 63. Consultado em 9 de novembro de 2016























![{\displaystyle \mathbb {E} \left[\varphi (X)\right]{\stackrel {\text{déf.}}{=}}\int _{\Omega }\varphi {\big (}X(\omega ){\big )}\mathbb {P} (\mathrm {d} \omega )=\int _{\mathbb {R} }\varphi (x)\mathbb {P} _{X}(\mathrm {d} x),}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c4ad97bc026c84c768efe3c24a1fa90be1477713)


![{\displaystyle \mathbb {E} \left[\varphi (X)\right]=\mathbb {E} \left[\varphi (Y)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/885e7731a6347edc000195e769b173b3999cde23)




































![{\displaystyle \mathbb {E} \left[\varphi (X)|Y\right]=\int \varphi (x)\mathbb {P} _{X|Y}(\mathrm {d} x)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7eaf8a0e5f85539c530ae8654d99a7c00e03091c)



![{\displaystyle \mathbb {E} \left[X|{\mathcal {G}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2b047bb458622f35497bd0b378b3b1d82ec3c19a)
![{\displaystyle \mathbb {E} \left[Z\mathbb {E} (X|{\mathcal {G}})\right]=\mathbb {E} \left[ZX\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b4a68f01eae65f27c2b7b93da93f785365810180)
































![{\displaystyle ]-\infty ,x[}](https://wikimedia.org/api/rest_v1/media/math/render/svg/261b8649a40b0a9688abe9c980bfb57534c5931d)










![{\displaystyle m_{n}=\mathbb {E} [X^{n}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/91cde357ac7466638096542ae55ceadddfd0bed6)













![{\displaystyle \{(\omega ,p(\omega ))\in \Omega _{a}\times ]0,1]\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/db8be31292fb88ffd029900198d992475308baa6)




![{\displaystyle \mathbb {E} \left[\varphi (X)\right]=\sum _{x\in \Omega _{a}}\varphi (x)p_{X}(x)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d395793da3cf9e7fa342e517597458022c4b33b3)





![{\displaystyle E[X]=a}](https://wikimedia.org/api/rest_v1/media/math/render/svg/14623ff7a6b37650cb5f7028d4eb418f31b65297)






![{\displaystyle E[X]={\frac {1}{k}}\sum _{i=1}^{k}x_{i}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dcf6d95f4d2039802f9243a1a36ce4cd416cfa80)


![{\displaystyle p\in [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/33c3a52aa7b2d00227e85c641cca67e85583c43c)







![{\displaystyle \operatorname {E} [X]=np}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8a847aa9a0c1fc2751c00a6b9cb4be55e784e88a)
![{\displaystyle \operatorname {Var} [X]=np(1-p)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/23eeb9e25ec727bf979d0432c8175efe6f2e319b)





![{\displaystyle E[X]={\frac {1}{p}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/db85df0d1c494b9c8488276e542ac7a055a92492)






![{\displaystyle E\left[X\right]=\lambda }](https://wikimedia.org/api/rest_v1/media/math/render/svg/c8dc215d84f28ce4435ba584260efe34297b6219)
![{\displaystyle \operatorname {Var} [X]=\lambda }](https://wikimedia.org/api/rest_v1/media/math/render/svg/9d16fefc078d61d56912bde3055f0a7944138055)









![{\displaystyle E[X]={\frac {nm}{N}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/33d1faecc373dee6ca9503c1a3c4c38a540a386e)






![{\displaystyle \mathbb {E} \left[\varphi (X)\right]=\int _{\mathbb {R} }\varphi (x)f_{X}(x)\,\mathrm {d} x.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5c81c4dc76bffe461a2bbd487654859d722259ec)
![{\displaystyle [c,d]\subset [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/436858b65bd15c818622b9648d4defd5244e559b)
![{\displaystyle [c,d]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d85b3b21d6d891d97f85e263d394e3c90287586f)

![{\displaystyle x\in [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/026357b404ee584c475579fb2302a4e9881b8cce)


![{\displaystyle \mathrm {E} [X]={\frac {\alpha +\beta }{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4d9c28de8cbeda39f88a56a732ffadd6261775a6)
![{\displaystyle \mathrm {Var} [X]={\frac {(\beta -\alpha )^{2}}{12}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d0ea66b8496654e62d1a7d5ceccfb68422587293)




![{\displaystyle \mathrm {E} [X]={\frac {1}{\lambda }}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5bb3aa18bb473919aac4d41f66b36d907af7bf66)
![{\displaystyle \mathrm {Var} [X]={\frac {1}{\lambda ^{2}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/254a04534566c9017a18094672bacc03f9ad1952)




![{\displaystyle \mathrm {E} [X]=\mu <\infty }](https://wikimedia.org/api/rest_v1/media/math/render/svg/35efe981556e9975c4a80976ed253457033702ee)
![{\displaystyle \mathrm {Var} [X]=\sigma ^{2}<\infty }](https://wikimedia.org/api/rest_v1/media/math/render/svg/d34d644c8b9b53b9b48f0716a608f165bf9d4cd5)


![{\displaystyle f(x;\theta )={\frac {1}{\pi }}{\frac {1}{\left[1+(x-\theta )^{2}\right]}},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c3dd5cf24e8f4af454b805b22a91d94a17646022)













![{\displaystyle \alpha ,\beta ,\gamma \in [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e0681abc934a74fa0c7a6871d63e1e0b78fffed4)




![{\displaystyle \alpha \in ]0,1[}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c8be4435dda6bb5e07a1d6f87c8010936a4e4250)

![{\displaystyle ]-\infty ,x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f971ac4c5d8ef52e3bed884b7ea254019baba8e6)



![{\displaystyle F(x)=\mathbb {P} {\big (}]-\infty ,x]{\big )}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d1cb12988d1186457233443e074bedba474595f1)





![{\displaystyle \Phi _{X}(t)=\int _{\mathbb {R} }\mathrm {e} ^{\mathrm {i} tx}\,\mathbb {P} _{X}(\mathrm {d} x)=\int _{\Omega }\mathrm {e} ^{\mathrm {i} tX(\omega )}\,\mathbb {P} (\mathrm {d} \omega )=\mathbb {E} \left[\mathrm {e} ^{\mathrm {i} tX}\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d8ab30c7b612196a03feaf60e34456621665846e)





![{\displaystyle M_{X}(t)=\int _{\mathbb {R} }\mathrm {e} ^{tx}\,\mathbb {P} _{X}(\mathrm {d} x)=\int _{\Omega }\mathrm {e} ^{tX(\omega )}\,\mathbb {P} (\mathrm {d} \omega )=\mathbb {E} \left[\mathrm {e} ^{tX}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c9ff25d0cc9030c9bd14689dafff0a413f7774dd)



![{\displaystyle p\in ]0,1[}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2cd07a5e96ded88e85782453bdae4353f369a648)






![{\displaystyle [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/738f7d23bb2d9642bab520020873cccbef49768d)





