Desvio padrão
| Estatística |
|---|
 |
Em probabilidade, o desvio padrão ou desvio padrão populacional (comumente representado pela letra grega ) é uma medida de dispersão em torno da média populacional de uma variável aleatória. O termo possui também uma acepção específica no campo da estatística, na qual também é chamado de desvio padrão amostral (comumente representado pela letra latina ) e indica uma medida de dispersão dos dados em torno de média amostral. Um baixo desvio padrão indica que os pontos dos dados tendem a estar próximos da média ou do valor esperado.[1] Um alto desvio padrão indica que os pontos dos dados estão espalhados por uma ampla gama de valores. O desvio padrão populacional ou amostral é a raiz quadrada da variância populacional ou amostral correspondente, de modo a ser uma medida de dispersão que seja um número não negativo e que use a mesma unidade de medida dos dados fornecidos.[2][3][4]
Tanto em probabilidade quanto em estatística, o desvio padrão é usado para expressar outros conceitos matemáticos importantes como o coeficiente de correlação, o coeficiente de variação ou a alocação ótima de Neyman, dentre outros. Há também outras medidas de desvio como o desvio médio absoluto, que fornecem propriedades matemáticas diferentes a partir do desvio padrão.[5] O desvio padrão é mais simples, porém mais robusto que o desvio médio absoluto na prática.[6][7] Além de expressar a variabilidade da população, o desvio padrão comumente é usado para medir a confiança em cálculos estatísticos e geralmente permite sintetizar os resultados de uma experiência repetida várias vezes.[8] Por exemplo, a margem de erro de um conjunto de dados é determinada pelo cálculo do desvio padrão da média ou do desvio padrão populacional inverso da raiz quadrada do tamanho da amostra, se a mesma pesquisa for repetida várias vezes.[9]
Esta derivação do desvio padrão geralmente é chamada de erro padrão da estimativa ou erro padrão da média (em referência à média). O erro padrão da média é calculado a partir do desvio padrão das médias, as quais poderiam ser computadas a partir de uma população se um número infinito de amostras e uma média para cada amostra fossem considerados. A margem de erro de uma pesquisa é calculada a partir do erro padrão da média (produto do desvio padrão populacional e do inverso da raiz quadrada do tamanho da amostra), e cerca do dobro do erro padrão da média é a metade da largura de 95% do intervalo de confiança para a média (populacional).[10]
O desvio padrão é calculado em todas as áreas que usam probabilidade e estatística, em particular biologia, finanças, física e pesquisas em geral. Em ciência, os pesquisadores comumente reportam o desvio padrão dos dados experimentais. Em geral, apenas os efeitos mais de dois desvios padrões distantes do esperado são considerados estatisticamente significativos – por meio de erro aleatório normal ou variação nas medições podem-se distinguir os efeitos prováveis dos efeitos genuínos.[11] Quando apenas uma amostra dos dados da população está disponível, o termo desvio padrão amostral pode referir-se tanto à quantidade mencionada acima quanto a uma quantidade modificada que seja uma estimativa não enviesada do desvio padrão populacional. Quando o desvio padrão populacional não é conhecido, o seu valor é aproximado por meio do desvio padrão amostral.[10]
História[editar | editar código-fonte]
O desvio padrão é uma grandeza que remete ao século XIX, no contexto do desenvolvimento da estatística no Reino Unido. Enquanto o conceito de medida de dispersão foi criado por Abraham de Moivre e usado em seu livro The Doctrine of Chances em 1718,[12] o termo desvio padrão foi pontualmente usado pela primeira vez por Karl Pearson em 1894,[13][14] em substituição a termos anteriores como erro médio, utilizado por Carl Friedrich Gauss.[15] O símbolo também foi utilizado pela primeira vez por Karl Pearson para representar o desvio padrão.[14]
Em 1908, William Gosset (mais conhecido sob o pseudônimo Student) definiu o desvio padrão empírico de uma amostra e mostrou que a distinção entre o desvio padrão amostral e o desvio padrão populacional é importante.[14] Somente em 1918, Ronald Aylmer Fisher definiu a noção da variância no texto The Correlation between Relatives on the Supposition of Mendelian Inheritance.[16]
Em probabilidade[editar | editar código-fonte]
Definição[editar | editar código-fonte]
Seja uma variável aleatória com média e valor esperado . Então, o desvio padrão de pela definição é a raiz quadrada da variância de ou a raiz quadrada do valor médio de [17]
A fórmula foi derivada a partir das propriedades da esperança.[17]
Desvio padrão de uma variável aleatória discreta[editar | editar código-fonte]
Quando é uma variável aleatória de um conjunto de dados finito , com cada valor tendo a mesma probabilidade , o desvio padrão é:
,
em que é a esperança da variável , sendo .[17]
Se os valores tiverem probabilidades diferentes em vez de probabilidade iguais (se tiver probabilidade , se tiver probabilidade , ... , se tiver probabilidade ), o desvio padrão é:
,
em que .[17]
Desvio padrão de uma variável aleatória contínua[editar | editar código-fonte]
O desvio padrão de uma variável aleatória contínua com função densidade é:
,
em que .[18]
No caso de uma família paramétrica de uma distribuição, o desvio padrão pode ser expresso em termos de parâmetros. Por exemplo, no caso da distribuição log–normal com parâmetros e , com com distribuição normal com parâmetros e , o desvio padrão é .[19]
Desvio padrão de distribuições de probabilidade conhecidas[editar | editar código-fonte]
| Distribuição | Parâmetros | Descrição | Desvio padrão |
|---|---|---|---|
| Distribuição de Bernoulli[20] | Distribuição discreta de valor 0 com probabilidade e 1 com probabilidade . | ||
| Distribuição binomial[21] | e | Distribuição da soma de variáveis independentes de acordo com a distribuição de Bernoulli de parâmetro . | |
| Distribuição geométrica[22] | Distribuição discreta em , tal que a probabilidade de se obter o número inteiro é . | ||
| Distribuição uniforme[23] | Distribuição uniforme contínua em , cuja densidade é um múltiplo da função indicadora de . | ||
| Distribuição exponencial[23] | Distribuição uniforme contínua com suporte , cuja densidade é a função. | ||
| Distribuição de Poisson[24] | Distribuição em , cuja densidade é a função , em que . | ||
| Distribuição qui-quadrado[25] | Distribuição em , cuja densidade é a função para todo positivo, em que é a função gama. | ||
| Distribuição gama[25] | , e | Distribuição de probabilidade contínua, cuja densidade é a função para todo positivo, em que é a função gama. |
O desvio padrão de uma distribuição de probabilidade univariada é igual ao desvio padrão de uma variável aleatória com a mesma distribuição. Nem todas as variáveis aleatórias possuem desvio padrão, uma vez que os valores esperados podem não existir. Por exemplo, o desvio padrão de uma variável que segue uma distribuição de Cauchy é indefinido porque seu valor esperado é indefinido.[26]
Propriedades[editar | editar código-fonte]
- O desvio padrão é sempre positivo ou nulo.[27] O desvio padrão de uma constante é nulo.[28]
- O desvio padrão de uma variável aleatória à qual foi adicionada uma constante é igual ao desvio padrão da variável aleatória , uma propriedade chamada invariante por translação.[28]
- O desvio padrão de uma variável multiplicada por uma constante positiva é igual à constante multiplicada pelo desvio padrão da variável, uma propriedade chamada invariante por dilatação, que pode ser resumida como . Propriedades como invariante de dilatação são consequências diretas do teorema de Huygens e das propriedades de valor esperado.[29]
- O desvio padrão da soma algébrica de duas variáveis é igual a , em que é o coeficiente de correlação entre as duas variáveis e .[30]
- O desvio padrão segue a desigualdade triangular . Existe igualdade se e somente se existe uma relação linear quase certa entre as duas variáveis . A desigualdade decorre da desigualdade anterior e da desigualdade .[31]
- A função admite o ponto mínimo . Portanto, assumindo–se no ponto o valor do desvio padrão da variável aleatória .[32]
Usos[editar | editar código-fonte]
Em probabilidade, o desvio padrão compara as variáveis ou as suas distribuições.[17]
Variável aleatória centrada reduzida[editar | editar código-fonte]

Se é uma variável aleatória com desvio padrão não nulo, é possível fazê–la corresponder à variável aleatória centrada reduzida. Duas variáveis aleatórias centradas e reduzidas e são fáceis de comparar, uma vez que e .[33]
O teorema central do limite é o limite de uma sequência de variáveis aleatórias centradas reduzidas,[34] os coeficientes de assimetria e a curtose de uma densidade de probabilidade e são usados para comparar diferentes distribuições.[35]
Coeficiente de correlação[editar | editar código-fonte]
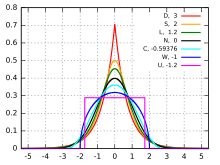
O coeficiente de correlação é outra aplicação do desvio padrão em probabilidade. Se e são duas variáveis aleatórias, o coeficiente de correlação , em que , é a covariância das variáveis aleatórias e . De acordo com a desigualdade de Cauchy–Schwarz , é possível afirmar que assume valores no intervalo .[36] Se , as duas variáveis aleatórias não são correlacionadas. Se , as duas variáveis aleatórias são linearmente dependentes.[37]



Desigualdade de Bienaymé–Chebyschev[editar | editar código-fonte]
É por meio da desigualdade de Bienaymé–Chebyschev que o desvio padrão aparece como uma medida de dispersão em torno da média. A desigualdade de Bienaymé–Chebyschev afirma que e mostra que a probabilidade de desviar–se de ao longo de desvios padrões é menor ou igual a .[38]
A desigualdade de Chebyschev afirma que, para todas as distribuições para as quais o desvio padrão é definido, o volume de dados dentro de uma quantidade de desvios padrões da média são pelo menos os mesmos que os da tabela a seguir.[39]
| Distância da média | População mínima |
|---|---|
| 50% | |
| 75% | |
| 89% | |
| 94% | |
| 96% | |
| 97% | |
| [40] |
Em estatística[editar | editar código-fonte]
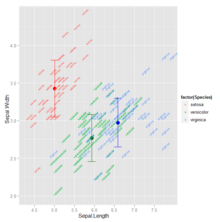
Para uma população finita e relativamente pequena, o cálculo do desvio padrão é puramente algébrico sem referência à probabilidade. A estatística utiliza o desvio padrão empírico definido por .[41]
Em estatística, a população é geralmente muito importante em número (não é possível conhecer todos os valores da população). Entre os recursos utilizados em amostragem e estimativa para avaliar os valores está o desvio padrão.[42]
Interpretação[editar | editar código-fonte]

Um grande desvio padrão indica que os pontos dos dados estão espalhados longe da média e um pequeno desvio padrão indica que os pontos dos dados estão agrupados perto da média. Por exemplo, cada uma das três populações {0, 0, 14, 14}, {0, 6, 8, 14} e {6, 6, 8, 8} possui média 7. Os desvios padrões são 7, 5 e 1, respectivamente. A terceira população tem um desvio padrão menor porque seus valores são próximos de 7.[43]
O desvio padrão tem a mesma unidade dos dados. Um exemplo, o conjunto de dados {0, 6, 8, 14} representa as idades de uma população de quatro irmãos em anos. A média é de 7 anos e o desvio padrão é de 5 anos. Outro exemplo, o conjunto de dados {1000, 1006, 1008, 1014} representa as distâncias percorridas por quatro atletas em metros. A média é de 1007 metros e o desvio padrão é de 5 metros.[44]
O desvio padrão pode servir como medida de incerteza. Em ciências, a precisão de medições repetidas é dada pelo desvio padrão. O desvio padrão é crucial para analisar se as medições batem com a previsão teórica. Se a média das medições estiver muito longe da previsão teórica (distância medida pelo desvio padrão), então a teoria testada provavelmente precisa ser revisada.[45]
Enquanto o desvio padrão mede a distância dos valores típicos da média, outras medidas estão disponíveis.[17] É o exemplo do desvio médio absoluto, que pode ser considerado uma medida mais direta da distância da média em comparação à distância da raiz quadrada média inerente ao desvio padrão.[46]
Interpretação geométrica[editar | editar código-fonte]
Seja uma população com três valores, . Seja um ponto em . Consideramos a linha que é a diagonal principal, partindo da origem. Se os três valores fossem iguais, então o desvio padrão seria 0 e o ponto estaria em . Então, pode–se assumir que o desvio padrão está relacionado à distância entre e . Para mover–se ortogonalmente de para , é preciso partir do ponto , cujas coordenadas são as médias dos valores mencionados acima.[47]
Derivação de
|
|---|
|
está em. Portanto com A linha deve ser ortogonal ao vetor de para . Portanto:
|
A distância entre e (igual à distância entre e ) é igual ao desvio padrão do vetor multiplicado pela raiz quadrada do número de dimensões do vetor (3 dimensões, no caso).[47]
Regras para dados distribuídos normalmente[editar | editar código-fonte]

De acordo com o teorema central do limite, a distribuição da média de muitas variáveis aleatórias distribuídas independentemente e identicamente tende à distribuição normal
com função densidade , em que é o valor esperado das variáveis aleatórias, é igual aos desvios padrões das distribuições dividido por e é o número de variáveis aleatórias. Portanto, o desvio padrão é simplesmente uma variável escalonada que ajusta a amplitude da curva, embora ele apareça também na constante de normalização. Se a distribuição dos dados é aproximadamente normal, então a proporção dos valores dos dados dentro do desvio padrão da média é definida pela função erro . Uma proporção que seja menor ou igual a um número é dada pela função cumulativa
.[48]
Se a distribuição dos dados é aproximadamente normal, então cerca de 68% dos valores dos dados estão dentro de um desvio padrão da média (, em que é a média aritmética), cerca de 95% estão dentro de dois desvios padrões () e cerca de 99,7% estão dentro de três desvios padrões (). Isto é conhecido como a regra empírica 68–95–99,7.[49]
Para vários valores de , as porcentagens dos valores esperados dentro ou fora do intervalo simétrico são:


| Intervalo de confiança | Proporção dentro | Proporção fora | |
|---|---|---|---|
| Porcentagem | Porcentagem | Fração | |
| 50% | 50% | ||
| 68% | 32% | ||
| 68,2689492% | 31,7310508% | ||
| 80% | 20% | ||
| 90% | 10% | ||
| 95% | 5% | ||
| 95,4499736% | 4,5500264% | ||
| 99% | 1% | ||
| 99,7300204% | 0,2699796% | ||
| 99,9% | 0,1% | ||
| 99,99% | 0,01% | ||
| 99,993666% | 0,006334% | ||
| 99,999% | 0,001% | ||
| 99,9993204653751% | 0,0006795346249% | ||
| 99.9999% | 0,0001% | ||
| 99,9999426697% | 0,0000573303% | ||
| 99,99999% | 0,00001% | ||
| 99,999999% | 0,000001% | ||
| 99,9999998027% | 0,0000001973% | ||
| 99,9999999% | 0,0000001% | ||
| 99,99999999% | 0,00000001% | ||
| 99,999999999% | 0,000000001% | ||
| 99,9999999997440% | 0,000000000256% | ||
Em resumo, de acordo com a regra 68–95–99,7, para uma distribuição normal unimodal, gaussiana, simétrica, de afunilamento médio (mesocúrtica):[49]
- 68% dos valores encontram–se a uma distância da média inferior a um desvio padrão;[50]
- 95% dos valores encontram–se a uma distância da média inferior a duas vezes o desvio padrão;[50]
- 99,7% dos valores encontram–se a uma distância da média inferior a três vezes o desvio padrão.[50]
Exemplos[editar | editar código-fonte]

Imagem 1: É construída a frequência da distribuição.
Imagem 2: O centroide da distribuição fornece a média. Imagem 3: Um quadrado com lados iguais à diferença de cada valor da média é formado para cada valor. Imagem 4: A organização dos quadrados em um retângulo com um lado igual ao número de valores resulta em outro lado igual à variância da distribuição .Desvio padrão populacional[editar | editar código-fonte]
Para um conjunto de dados finito, o desvio padrão é calculado a partir da raiz quadrada da média dos desvios entre os valores e a média dos valores dos dados elevado ao quadrado.[51]
Sejam as notas de 8 estudantes () 2, 4, 4, 4, 5, 5, 7, 9. A média das notas dos 8 estudantes é: .
Os desvios entre as notas e a média das notas elevados ao quadrado são:
A variância ou a média de todos os valores é: . O desvio padrão ou a raiz quadrada da variância é . Isto é, o desvio padrão é igual a 2.[51]
Desvio padrão amostral[editar | editar código-fonte]
O cálculo da raiz quadrada da média dos desvios entre os valores e a média dos valores dos dados elevados ao quadrado é válido apenas se os valores formarem a população total. Se os valores forem parte de uma amostra aleatória extraída de uma população maior (por exemplo, 8 notas extraídas de uma sala de aula de 2 milhões de estudantes), então o denominador da fórmula da variância seria (7) em vez de (8) e o resultado seria chamado desvio padrão amostral.[52]
A divisão da soma dos desvios entre as notas e a média das notas por em vez de fornece uma estimativa não enviesada do desvio padrão populacional maior, o que é conhecido como correção de Bessel.[53]
Seja a altura média de um homem adulto nos Estados Unidos 1,78 metro ou 178 centímetros, com desvio padrão de 7 centímetros. Então, a maioria dos homens adultos dos Estados Unidos (cerca de 68%) tem entre 7 centímetros acima e 7 centímetros abaixo de 178 centímetros (entre 171 centímetros e 185 centímetros, correspondente a um desvio padrão) e praticamente todos os homens adultos dos Estados Unidos (cerca de 95%) tem entre 14 centímetros acima e 14 centímetros abaixo de 178 centímetros (entre 164 centímetros e 192 centímetros, correspondente a dois desvios padrões). Se o desvio padrão fosse 0 centímetro, então todos os homens adultos dos Estados Unidos teriam 178 centímetros. Se o desvio padrão fosse 50 centímetros, então os homens adultos dos Estados Unidos teriam uma variação muito maior de altura (entre 121 centímetros e 221 centímetros). Três desvios padrões representam 99,7% da amostra da população estudada, assumindo que é uma distribuição normal (em forma de sino).[52][53]
Estimadores[editar | editar código-fonte]
Um estimador é uma função que aproxima–se de um parâmetro de uma população por meio de uma amostra aleatória.[54] Dois estimadores do desvio padrão são geralmente utilizados. Os estimadores ou e ou são expressos em função dos valores da amostra por
e .
é o estimador não enviesado.[55][56]
Na verdade, uma boa estimativa do desvio padrão real seria , em que é a média da distribuição de . Muitas vezes a média não é conhecida e precisa ser calculada a partir da amostra pela fórmula . Então, a estimativa do desvio padrão é calculado pela fórmula
.[57]
O denominador é em vez de (correção de Bessel) porque o cálculo da média de a partir da amostra perdeu um grau de liberdade, uma vez que a fórmula liga aos valores . Portanto, há apenas valores independentes após o cálculo de .[57]
Propriedades dos estimadores[editar | editar código-fonte]
Duas propriedades importantes dos estimadores são a convergência e a falta de viés.[56] Se é um estimador do parâmetro , o viés será a quantidade . Se o valor for diferente de zero, significa que está posicionado em torno de em vez de . O estimador é contaminado pelo erro. Um bom estimador não tem viés.[58] O estimador do desvio padrão é enviesado, mas o viés é aceitável.[59][60]
Se , então converge (em distribuição, em média, em probabilidade, quase certamente) para à medida que aproxima-se do infinito. Entretanto, se e são estimadores convergentes de , reflete–se a aproximação de para as duas séries quando torna–se cada vez maior.[58] Com o teorema da continuidade afirmando que se é contínua (limite em probabilidade), a função raiz quadrada é contínua, os estimadores e são convergentes também. O teorema da continuidade afirma que se é ume função contínua, então , em que denota convergência em probabilidade. Como a função raiz quadrada é uma função contínua, e são estimadores convergentes do desvio padrão. Isto é, e .[61]
Desvio padrão da média[editar | editar código-fonte]
A média e o desvio padrão de um conjunto de dados são estatísticas descritivas geralmente reportadas em conjunto. De uma certa maneira, o desvio padrão é uma medida natural de dispersão estatística se o centro dos dados for medido em relação à média. Isto porque o desvio padrão a partir da média é menor que o desvio padrão a partir de qualquer outro ponto. Sendo números reais, define–se a função Usando cálculo ou completamento de quadrado, é possível mostrar que tem um mínimo único na média [62]
A variabilidade também pode ser medida pelo coeficiente de variação, que é a razão entre o desvio padrão e a média. É um número adimensional.[63]
Geralmente quer-se mais informações sobre a precisão da média obtida. Podemos obtê-la determinando o desvio padrão da média amostral. Assumindo a independência estatística dos valores na amostra, o desvio padrão da média está relacionado ao desvio padrão da distribuição por , em que é o número de observações na amostra usado para estimar a média.[64]
Isto pode ser provado com Isto resulta em [65]
É importante ressaltar que para estimar o desvio padrão da média é necessário saber o desvio padrão de toda a população de antemão. Entretanto, este parâmetro é desconhecido na maioria das aplicações. Por exemplo, se uma série de 10 medições de uma quantidade previamente desconhecida é realizada em um laboratório, é possível calcular a média da amostra resultante e o desvio padrão amostral, mas é impossível calcular o desvio padrão da média.[66]
Para estimar a exatidão da estimativa da média de uma variável, o método do cálculo do desvio padrão da distribuição da amostragem das médias é utilizado. Também chamado erro padrão da média e denotado como , é o desvio padrão das médias das amostras de tamanho idêntico de uma população. Se é o tamanho das amostras tomadas a partir do desvio padrão de uma população e se é o tamanho da população, então .[67]
Quando o desvio padrão da população é desconhecido, ele pode ser substituído pelo estimador .[67] Quando é suficientemente grande (), a distribuição da amostra provavelmente segue a lei de Laplace–Gauss, que permite deduzir um intervalo de confiança em função de para localizar a média da população a partir da média da amostra.[68][69]
Há casos em que é possível encontrar o desvio padrão de uma população inteira com o Teste Z, em que cada membro da população é amostrado. Em casos em que não é possível encontrar o desvio padrão , ele é estimado analisando uma amostra padrão extraída da população e calculando uma estatística da amostra, que é usada como uma estimativa do desvio padrão populacional.
Entretanto, ao contrário da estimativa da média da população, para a qual a média amostral é um estimador simples com muitas propriedades desejáveis (não enviesado, eficiente, máxima verossimilhança), não há um único estimador para o desvio padrão com todas estas propriedades, além de que um estimador não enviesado do desvio padrão é um problema técnico. Frequentemente o desvio padrão é estimado usando o desvio padrão corrigido da amostra e geralmente é referido como o desvio padrão amostral, sem qualificadores. Porém, outros estimadores são melhores em outros aspectos − o estimador com a correção () produz um erro quadrático médio mais baixo, enquanto o uso de correção para distribuição normal elimina quase completamente o viés.[70]
Desvio padrão não corrigido da amostra[editar | editar código-fonte]
Primeiramente, a fórmula para o desvio padrão populacional de uma população finita pode ser aplicada à amostra usando o tamanho da amostra como o tamanho da população (embora o tamanho verdadeiro da população da qual a amostra é extraída possa ser muito maior). O estimador denotado como é conhecido como desvio padrão não corrigido da amostra ou às vezes como desvio padrão amostral (considerado com a população inteira) e é definido como em que são os valores observados dos itens da amostra, é o valor da amostra das observações, é o tamanho da amostra (raiz quadrada da variância da amostra, que é a média dos desvios quadráticos da média da amostra).[71]
é um estimador consistente (converge em probabilidade para os valores da população à medida que o número de amostras tende ao infinito) e é a estimativa por máxima verossimilhança quando a população é normalmente distribuída. Entretanto, é um estimador enviesado na medida em que as estimativas são geradas muito lentamente. O viés diminui conforme o tamanho da amostra aumenta, caindo para e, portanto, é mais significativo para tamanhos pequenos ou moderados de amostras. Para , o viés é menor que 1%. Então, para tamanhos muito grandes de amostras, o desvio padrão não corrigido da amostra é geralmente aceitável. O estimador também tem erro quadrático médio uniformemente menor que o desvio padrão corrigido da amostra.[71]
Desvio padrão corrigido da amostra[editar | editar código-fonte]
Se a variância enviesada da amostra (o segundo momento central da amostra, que é uma estimativa tendenciosa da variância populacional) é usada para calcular uma estimativa do desvio padrão populacional, retirando a raiz quadrada, introduzem-se mais vieses tendenciosos pela desigualdade de Jensen devido à raiz quadrada ser uma função côncava. O viés na variância é facilmente corrigido, mas o viés da raiz quadrada é mais difícil de ser corrigido e depende da distribuição em questão.
Um estimador não enviesado da variância é dado pela aplicação da correção de Bessel, usando em vez de para gerar a estimativa da variância não enviesada da amostra denotada como [72] Retirando a raiz quadrada, reintroduz-se o viés porque a raiz quadrada é uma função não linear, que não é comutativa com a expectativa. Isto gera o desvio padrão corrigido da amostra denotado como [72]
Enquanto é uma estimativa não enviesada da variância populacional, é uma estimativa enviesada do desvio padrão populacional. Embora notadamente menos enviesado que o desvio padrão não corrigido da amostra. O viés continua sendo significativo para pequenas amostras () e também cai para à medida que o tamanho da amostra aumenta. Este estimador é comumente usado e geralmente conhecido simplesmente como desvio padrão amostral.[72]
Desvio padrão não enviesado da amostra[editar | editar código-fonte]
Para estimativas não enviesadas do desvio padrão, não há fórmula que aplique-se a todas as distribuições, ao contrário da média e da variância. é usado como uma base e é escalado por um fator de correção para produzir uma estimativa não enviesada. Para a distribuição normal, um estimador não enviesado é dado por , em que o fator de correção que depende de é dado em termos da função gama:
Isto ocorre porque a distribuição amostral do desvio padrão amostral segue uma distribuição qui e o fator de correção é a média da distribuição qui. Uma aproximação pode ser dada pela substituição de por , tal que [70]
O erro na aproximação cai quadraticamente para , e é adequado para todas as amostras, com exceção daquelas menores ou de menor precisão. Para , o viés é igual a 1,3% e para o viés é menor que 0,1%. Para outras distribuições, a fórmula correta depende da distribuição, mas uma regra de ouro é usar o refinamento da aproximação:
em que denota o excesso de curtose da população, que pode ser tanto conhecido antecipadamente para certas distribuições quanto estimado a partir dos dados.[70]
Intervalo de confiança para o desvio padrão amostral[editar | editar código-fonte]
O desvio padrão obtido a partir da distribuição amostral não é absolutamente preciso, tanto por razões matemáticas (aqui explicadas pelo intervalo de confiança) quanto por razões práticas de medição (erro de medição). O efeito matemático pode ser descrito pelo intervalo de confiança.[73] Para mostrar como uma amostra maior tornará o intervalo de confiança menor, consideram-se os seguintes exemplos.
Uma pequena população de tamanho = 3 tem apenas um grau de liberdade para estimar o desvio padrão. O resultado é que um intervalo de confiança de 95% tem desvio padrão entre 0,45 e 31,90. Os fatores são em que é o −ésimo quantil da distribuição qui−quadrado com graus de liberdade e é o nível de confiança. Isto é equivalente a [74]
Com , e . As recíprocas da raiz quadrada destes dois números fornecem os fatores 0,45 e 31,90 mencionados acima.
Uma população maior de tamanho tem 9 graus de liberdade para estimar o desvio padrão. Os mesmos cálculos acima fornecem um intervalo de confiança de 95% com desvio padrão entre 0,88 e 1,16. Para ter mais certeza de que o desvio padrão amostral será próximo do desvio padrão real, é preciso amostrar um grande número de pontos. As mesmas fórmulas podem ser usadas para obter os intervalos de confiança da variância de resíduos a partir do método dos mínimos quadrados, que se encaixa na teoria normal padrão, em que é o número de graus de liberdade do erro.[74]
Desvio padrão de desvio padrão empírico[editar | editar código-fonte]
Em geral, é muito difícil calcular a distribuição de probabilidade de desvio padrão empírico. Porém se é uma sequência de variáveis aleatórias distribuídas de acordo com a distribuição normal , então segue uma distribuição de a graus de liberdade.[75] Esta lei é o desvio padrão . Portanto, o desvio padrão da distribuição das variações das variáveis normais é expresso por .[75]
Interpretação de um desvio padrão elevado[editar | editar código-fonte]
O conceito de desvio padrão elevado não tem sentido isoladamente. Ele não indica uma dispersão forte que se torna o valor adimensional quando dividido pela média.[4] Um desvio padrão elevado possivelmente pode indicar a existência de um outlier. Um critério consiste em rejeitar os valores que diferem da média em mais de três vezes o desvio padrão, o qual está sob a distribuição normal de uma probabilidade de exceder de .[76]
Pesquisas de opinião[editar | editar código-fonte]
Em pesquisas de opinião, o desvio padrão avalia a incerteza das variações acidentais de inerentes à pesquisa, chamada de margem de erro devido às variações acidentais.[77]
Com o método da amostragem representativa, quando os diferentes estratos têm desvios padrões muito diferentes, o desvio padrão é utilizado para calcular a repartição ótima de Neyman, que permite medir a população nos diferentes estratos em função do desvio padrão. Em outros termos, é o tamanho da amostragem do estrato, é o tamanho total do estrato, é o tamanho do estrato e é o desvio padrão do estrato .[77]
Em algoritmo[editar | editar código-fonte]
O cálculo do desvio padrão para um programa de computador pode resultar em dados inconsistentes quando não se utiliza um algoritmo adequado, como quando se utiliza o algoritmo que opera diretamente a fórmula de grandes amostras de valores entre 0 e 1.[78][79]
Um dos melhores algoritmos é chamado B.P. Welford, descrito por Donald Knuth em seu livro The Art of Computer Programming Vol. 2.[80][81] Uma aproximação do desvio padrão da direção do vento é dada pelo algoritmo de Yamartino, que é usado em anemômetros modernos.[82][83]
Métodos de cálculos rápidos[editar | editar código-fonte]
As duas fórmulas seguintes podem representar um desvio padrão repetidamente atualizado. Um conjunto de duas somas de potências e são calculadas sobre um conjunto de valores de denotados como , Dados os resultados das duas somas, os valores , e podem ser usados a qualquer hora para calcular o valor atual do desvio padrão , em que é o tamanho do conjunto de valores (também pode ser denotado como ), como mencionado acima. Similarmente para o desvio padrão
Em uma implementação de computador, à medida que as três somas aumentam, é preciso considerar o erro de arredondamento, o overflow aritmético e o underflow aritmético. O método abaixo calcula o método das somas correntes com erros de arredondamento reduzidos. Isto é um algoritmo para calcular a variância de amostras sem a necessidade de armazenar dados anteriores durante o cálculo.[80] Aplicando este método a uma série de tempo, resultará em valores sucessivos de desvio padrão correspondente a pontos dados à medida que aumenta com cada nova amostra.
Para
, em que é o valor médio.
, em que desde que ou .
A variância da amostra é . A variância da população é .
Cálculo ponderado[editar | editar código-fonte]
Quando os valores são ponderados com pesos desiguais , as somas de potências , e são calculadas como As equações de desvio padrão continuam inalteradas, com a diferença de que passa a ser a soma dos pesos em vez do número de observações . O método incremental com erros de arredondamento reduzidos também pode ser aplicado, com alguma complexidade adicional. Uma soma de pesos deve ser computada para cada , de 1 até .
Os locais em que é usado devem ser substituídos por .
.
Na divisão final, e ou em que é o número total de elementos e é o número de elementos com pesos diferente de 0. As fórmulas mencionadas acima tornam-se iguais às fórmulas mais simples também mencionadas acima se os pesos forem tomados como iguais a 1.
Aplicações[editar | editar código-fonte]
O desvio padrão é usado como medida de dispersão de um conjunto de dados. Quanto menor o desvio padrão, mais os valores são agrupados em torno da média.[43] Seja a distribuição de notas entre os estudantes de uma sala de aula. Quanto menor o desvio padrão, mais homogêneas serão as notas. Quanto maior o desvio padrão, menos homogêneas serão as notas. Se as notas forem classificadas de 0 a 20, o desvio padrão mínimo será 0 (se todas as notas forem idênticas) e o desvio padrão máximo será 5 (se metade da classe tirar 0 e metade da classe tirar 20). Se estudantes tirarem 0 e estudantes tirarem 10, de modo que a amostra contenha vezes a nota 0 e vezes a nota 10, então a média será ou e . Os valores quadrados são e . A média de é . Portanto, a variância é 100 e o desvio padrão é 10.[43]
Testes experimentais, industriais e de hipóteses[editar | editar código-fonte]
Na indústria, o desvio padrão é usado para calcular o índice de fidelidade de um aparelho de medida ou o índice de qualidade de um produto.[84][85] Por exemplo, os pesos dos produtos de uma linha de produção precisam cumprir um valor exigido legalmente. Pesando uma fração dos produtos, é possível calcular o peso médio que sempre será um pouco diferente da média de longo prazo. Usando o desvio padrão, é possível encontrar um valor máximo e um valor mínimo para que o peso médio esteja dentro de uma porcentagem muito alta de tempo (igual ou maior que 99,9%). Se o desvio padrão ficar fora do intervalo, então o processo de produção precisa ser corrigido. Estes testes estatísticos são particularmente importantes quando o teste é relativamente caro.[84][85]
Na ciência, é comum considerar que os valores são distribuídos de acordo com a curva de Gauss. Nas ciências sociais, a média e o desvio padrão determinam o intervalo em que existe a maioria da população. Se a média for e o desvio padrão for , então 95% da população estará no intervalo e 68,2% da população estará no intervalo .[86]

O desvio padrão também é usado para formar um intervalo de confiança de uma amostra. Na imagem ao lado, há um desvio nos dois lados da média de 68,2% da distribuição, dois desvios , 3 desvios e assim por diante.[87]
Em um exemplo na física de partículas, o padrão 5 sigma é usado para considerar o resultado significativo. O padrão 5 sigma traduz uma chance em 3,5 milhões de uma flutuação aleatória afetar o resultado, o que representa uma probabilidade de erro inferior a 0,00003 % (nível de confiança superior a 99.99997%).[88] Este nível de certeza foi requerido para declarar a primeira detecção de ondas gravitacionais[89][90] e garantir a descoberta de uma partícula consistente com bóson de Higgs em dois experimentos independentes na Organização Europeia para a Pesquisa Nuclear (CERN).[91]
Em outro exemplo na mecânica quântica, o princípio da incerteza de Heisenberg afirma que o produto dos desvios padrões da posição e o impulso de uma partícula é maior ou igual que a constante de Planck dividida por dois .[92]
Finanças[editar | editar código-fonte]
Em finanças, o desvio padrão da taxa de retorno de investimento é uma medida da volatilidade do investimento, ou uma medida de risco associada às flutuações de preço de um determinado ativo ou ao risco de uma carteira de ativos.[93] O risco é um fator importante para gerenciar efetivamente uma carteira de investimentos porque ele determina a variação dos retornos sobre ativos e / ou sobre carteiras de ativos e fornece aos investidores uma base matemática para decisões de investimentos (teoria moderna do portfólio). O risco é medido pelo desvio padrão do retorno esperado sobre os preços de acordo com o modelo de precificação de ativos financeiros de Harry Markowitz.[94] Em análise técnica dos preços das ações, o desvio padrão fornece uma estimativa quantificada da incerteza dos retornos futuros. Quanto maior o retorno esperado sobre o investimento, maior o risco. Em outras palavras, investidores devem estimar o retorno esperado e a incerteza de retornos futuros.[95]
Seja um investidor que precise escolher entre duas ações. A ação A tem um retorno médio de 10% em 20 anos, com desvio padrão de 20 pontos percentuais. A ação B tem um retorno médio de 12% no mesmo período, com desvio padrão de 30 pontos percentuais. Com base no risco e no retorno, um investidor pode decidir pela ação A pelo retorno médio adicional de 12% não compensar o desvio padrão adicional de 10 pontos percentuais (risco ou incerteza maior sobre o retorno esperado). O investimento inicial da ação B deve ser menor que o investimento inicial da ação A. O retorno da ação B deve ser em média 2% maior que o retorno da ação A. A ação A deve ganhar 10% com 10 pontos percentuais para cima ou para baixo (variação de 30% para 10%), cerca de dois terços do retorno dos anos futuros. Quando são considerados possíveis retornos ou possíveis resultados mais extremos no futuro, um investidor deve esperar resultado de até 10% com 60 pontos percentuais para cima ou para baixo (variação de 70% para 50%), que inclui resultados para três desvios padrões a partir do retorno médio (cerca de 99,7% do possível retorno).[96][97]
Calculando a média aritmética do retorno de um título em um determinado período, obtém-se o retorno esperado do ativo. Subtraindo o retorno esperado do retorno real em cada período, obtém-se a diferença a partir da média. Elevando a diferença em cada período ao quadrado e retirando a média, obtém-se a variância total do retorno do ativo. Quanto maior a variância, maior o risco do título. Encontrando a raiz quadrada da variância, obtém-se o desvio padrão da ferramenta de investimento em questão.[96][97]

Séries temporais financeira são conhecidas por serem séries não estacionárias, enquanto os cálculos estatísticos acima como o desvio padrão aplicam–se apenas às séries estacionárias. Para aplicá–los às séries não estacionárias, as séries precisam ser transformadas em séries estacionárias, permitindo o uso de ferramentas estatísticas que agora possuem uma base válida para trabalhar.[98][99]
A análise de Bollinger é uma ferramenta que facilita a análise de previsões do mercado. John Bollinger construiu a curva de deslocamento da média para vinte dias e as curvas, de cada lado da curva de deslocamento da média, situadas a duas vezes o desvio padrão dos vinte dias.[100] O desvio padrão populacional é usado para estabelecer a largura das bandas de Bollinger. A banda de Bollinger ao lado é denotada como . O valor mais comumente usado para é 2. Há cerca de 5% de chance de o valor ser diferente, assumindo uma distribuição normal dos retornos.[101]
Tempo[editar | editar código-fonte]
Sejam as temperaturas máximas médias diárias de duas cidades, uma no continente e outra na costa. O intervalo das temperaturas máximas diárias das cidades perto da costa é menor que as temperaturas máximas diárias das cidades no continente.[102] Portanto, enquanto cada uma das duas cidades pode ter a mesma temperatura máxima média, o desvio padrão da temperatura máxima diária da cidade da costa será muito menor que a temperatura máxima diária da cidade no continente. Em qualquer dia particular, é mais provável que a temperatura máxima real seja mais afastada da temperatura máxima média da cidade no continente que da temperatura máxima média da cidade na costa.[102]
Ver também[editar | editar código-fonte]
Referências
- ↑ Bland, J. Martin; Altman, Douglas G. «Measurement Error» (PDF). BMJ. Consultado em 23 de janeiro de 2017
- ↑ Saporta, Gilbert (2006). Probabilités – Analyse des Données et Statistiques. Paris: Éditions Technip. p. 25. 622 páginas
- ↑ Saporta, Gilbert (2006). Probabilités – Analyse des Données et Statistiques,. Paris: Éditions Technip. p. 119. 622 páginas
- ↑ a b Saporta, Gilbert (2006). Probabilités – Analyse des Données et Statistiques. Paris: Éditions Technip. p. 121. 622 páginas
- ↑ Gorard, Stephen (2004). «Revisiting a 90–year–old Debate: The Advantages of the Mean Deviation». Department of Educational Studies, University of York. Consultado em 23 de janeiro de 2017
- ↑ Gauss, Carl Friedrich (1816). «Bestimmung der Genauigkeit der Beobachtungen». Zeitschrift für Astronomie und verwandte Wissenschaften: 187 – 197
- ↑ Walker, Helen (1931). Studies in the History of the Statistical Method. [S.l.]: Baltimore, MD: Williams & Wilkins Co. p. 24 – 25
- ↑ Matos, Maria Auxiliadora Costa (2012). «Erro e Tratamento de Dados Analíticos» (PDF). Universidade Federal de Juiz de Fora (UFJF). Consultado em 2 de fevereiro de 2017
- ↑ «Margem de Erro / Determinação do Tamanho da Amostra» (PDF). University of Delaware – Departments of Electrical & Computer Engineering and Computer & Information Sciences. Consultado em 2 de fevereiro de 2017
- ↑ a b Viali, Lori. «Amostragem e Estimação» (PDF). Pontifícia Universidade Católica do Rio Grande do Sul (PUC – RS). Consultado em 2 de fevereiro de 2017
- ↑ Danelon, Maria Cristina Tavares de Moraes; Sampaio, Nilo Antonio de Souza. «Aplicações da Estatística nas Ciências» (PDF)
- ↑ Bernstein, Peter L. (1996). Against the Gods: The Remarkable Story of Risk. [S.l.]: John Wiley & Sons. p. 127. 383 páginas
- ↑ Pearson, Karl (1894). «On the Dissection of Asymmetrical Frequency Curves». A Philosophical Transactions of the Royal Society. 185: 71 – 110
- ↑ a b c Dodge, Yadolah (2010). The Concise Encyclopaedia of Statistics. New York: Springer. p. 506. 622 páginas
- ↑ Miller, Jeff. «Earliest Known Uses of Some of the Words of Mathematics». Consultado em 23 de janeiro de 2017
- ↑ Fisher, Ronald Aylmar (1918). «The Correlation between Relatives on the Supposition of Mendelian Inheritance» (PDF). Philosophical Transactions of the Royal Society of Edinburgh. 52: 99 – 433. Consultado em 23 de janeiro de 2017
- ↑ a b c d e f Pinheiro, João Ismael D.; Carvajal, Santiago S. Ramírez; Cunha, Sonia Baptista da; Gomes, Cunha Gastão Coelho (2012). Probabilidade e Estatística – Quantificando a Incerteza. [S.l.]: Elsevier. p. 56
- ↑ Pinheiro, João Ismael D.; Carvajal, Santiago S. Ramírez; Cunha, Sonia Baptista da; Gomes, Gastão Coelho (2012). Estatística e Probabilidade – Quantificando a Incerteza. [S.l.]: Elsevier. p. 87 – 88
- ↑ «lognstat». MathWorks. p. 1. Consultado em 23 de março de 2017
- ↑ Saporta, Gilbert (2006). Probabilités – Analyse des Données et Statistiques. Paris: Éditions Technip. p. 30. 622 páginas
- ↑ Saporta, Gilbert (2006). Probabilités – Analyse des Données et Statistiques. Paris: Éditions Technip. p. 31. 622 páginas
- ↑ Saporta, Gilbert (2006). Probabilités – Analyse des Données et Statistiques. Paris: Éditions Technip. p. 38. 622 páginas
- ↑ a b Saporta, Gilbert (2006). Probabilités – Analyse des Données et Statistiques. Paris: Éditions Technip. p. 39. 622 páginas
- ↑ Saporta, Gilbert (2006). Probabilités – Analyse des données et Statistiques. Paris: Éditions Technip. p. 33. 622 páginas
- ↑ a b Dodge, Yadolah (2010). The Concise Encyclopaedia of Statistics. New York: Springer. p. 71. 622 páginas
- ↑ Dodge, Yadolah (2010). The Concise Encyclopaedia of Statistics. New York: Springer. p. 60. 622 páginas
- ↑ «Roteiro de Cálculo de Incertezas Análise de Experimentos Virtuais» (PDF). Instituto de Física da Universidade de São Paulo (IF / USP). Consultado em 2 de fevereiro de 2017
- ↑ a b Becker, João Luiz (2015). Estatística Básica – Transformando Dados em informação. [S.l.]: Bookman. p. 65
- ↑ Saporta, Gilbert (2006). Probabilités – Analyse des Données et Statistiques. Paris: Éditions Technip. p. 23 – 25. 622 páginas
- ↑ Saporta, Gilbert (2006). Probabilités – Analyse des Données et Statistiques. Paris: Éditions Technip. p. 26. 622 páginas
- ↑ «Linear Algebra» (PDF). UNIVERSITY OF WISCONSIN-MADISON. 19 de março de 2013. p. 60. Consultado em 23 de março de 2017
- ↑ Rioul, Olivier (2008). Théorie des Probabilités. Paris: Éditions Hermes Sciences. p. 146. 364 páginas
- ↑ Gautier, C.; Girard, G.; Gerll, D.; Thiercé, C.; Warusfel, A. (1975). Aleph1 Analyse. Paris: Éditions Hachette. p. 387. 465 páginas
- ↑ Saporta, Gilbert (2006). Probabilités – Analyse des Données et Statistiques. Paris: Éditions Technip. p. 66. 622 páginas
- ↑ Rioul, Olivier (2008). Théorie des Probabilités. Paris: Éditions Hermes Sciences. p. 157. 364 páginas
- ↑ Rioul, Olivier (2008). Théorie des Probabilités. Paris: Éditions Hermes Sciences. p. 175. 364 páginas
- ↑ Rioul, Olivier (2008). Théorie des Probabilités. Paris: Éditions Hermes Sciences. p. 178. 364 páginas
- ↑ Jacquard, Albert (1976). Les Probabilités. Paris: Presses Universitaires de France. p. 28 – 29. 125 páginas
- ↑ «The Standard Deviation and the Distribution of Data Values: The Empirical Rule and Tchebysheff's Theorem» (PDF)
- ↑ Ghahramani, Saeed (2000). Fundamentals of Probability. New Jersey: Prentice Hall. 438 páginas
- ↑ Saporta, Gilbert (2006). Probabilités – Analyse des Données et Statistiques. Paris: Éditions Technip. p. 279 – 280. 622 páginas
- ↑ Rocha, Hermano Alexandre Lima; Carvalho, Eduardo Rebouças. «Conceitos Básicos em Epidemiologia e Bioestatística» (PDF). Faculdade de Medicina da Universidade Federal do Ceará (UFC). Consultado em 3 de fevereiro de 2017
- ↑ a b c Matos, Maria Auxiliadora Costa (2013). «Erro e Tratamento de Dados Analíticos» (PDF). Universidade Federal de Juiz de Fora (UFJF). Consultado em 6 de fevereiro de 2017. Arquivado do original (PDF) em 7 de fevereiro de 2017
- ↑ Ross, Sheldon (2004). Introduction to Probability and Statistics for Engineers and Scientists. [S.l.]: Elsevier. p. 24
- ↑ Tabacniks, Manfredo H. «Conceitos Básicos da Teoria de Erros» (PDF). Universidade de São Paulo (USP). Consultado em 20 de março de 2017
- ↑ Viali, Lorí. «Descritiva» (PDF). Pontifícia Universidade Católica do Rio Grande do Sul (PUC – RS). Consultado em 6 de fevereiro de 2017
- ↑ a b Diniz, Alexandre. «Estatística Espacial» (PDF). Universidade federal de Minas Gerais. p. 5. Consultado em 23 de março de 2017
- ↑ Weisstein, Eric W. «Distribution Function». MathWorld — A Wolfram Web Resource. Consultado em 24 de janeiro de 2017
- ↑ a b Ross, Sheldon (2004). Introduction to Probability and Statistics for Engineers and Scientists. [S.l.]: Elsevier. p. 32 – 33
- ↑ a b c «Erros». Instituto Tecnológico de Aeronáutica (ITA). Consultado em 20 de março de 2017
- ↑ a b Martins, Maria Eugénia Graça. «Desvio Padrão Amostral» (PDF). Revista de Ciência Elementar. 1 (1). Consultado em 6 de fevereiro de 2017
- ↑ a b Glantz, Stanton A. (2014). Princípios de Bioestatística. [S.l.]: AMGH. p. 16
- ↑ a b Weisstein, Eric W. «Bessel's Correction». MathWorld — A Wolfram Web Resource. Consultado em 24 de janeiro de 2017
- ↑ Saporta, Gilbert (2006). Probabilités – Analyse des Données et Statistiques. Paris: Éditions Technip. p. 289. 622 páginas
- ↑ Tufféry, Stéphane (2010). Data Mining et Statistique Décisionnelle. Paris: Éditions Technip. p. 655. 705 páginas
- ↑ a b Saporta, Gilbert (2006). Probabilités – Analyse des Données et Statistiques. Paris: Éditions Technip. p. 279 – 280. 622 páginas
- ↑ a b Lima, Carlos R. A. (março de 2004). «Teoria de Medidas – Erros e Gráficos» (PDF). Universidade Federal de Juiz de Fora (UFJF). Consultado em 20 de março de 2017
- ↑ a b Saporta, Gilbert (2006). Probabilités – Analyse des Données et Statistiques. Paris: Éditions Technip. p. 290. 622 páginas
- ↑ Saporta, Gilbert (2006). Probabilités – Analyse des Données et Statistiques. Paris: Éditions Technip. p. 284. 622 páginas
- ↑ Grenier, Emmanuel. «Quelle Est la Bonne Formule de L'écart–Type?» (PDF). Consultado em 24 de janeiro de 2017
- ↑ Rioul, Olivier (2008). Théorie des Probabilités. Paris: Éditions Hermes Sciences. p. 253. 364 páginas
- ↑ «Desvio Padrão da Média». Instituto Tecnológico de Aeronáutica (ITA). Consultado em 6 de fevereiro de 2016
- ↑ Pinheiro, João Ismael D.; Carvajal, Santiago S. Ramírez; Cunha, Sonia Baptista da; Gomes, Gastão Coelho (2012). Estatística e Probabilidade – Quantificando a Incerteza. [S.l.]: Elsevier. p. 57
- ↑ «Estimação para Média» (PDF). Instituto de Matemática e Estatística da Universidade de São Paulo (IME / USP). Consultado em 6 de fevereiro de 2016
- ↑ «Roteiro de Cálculo de Incertezas – Análise de Experimentos Virtuais» (PDF). Universidade de São Paulo (USP). Consultado em 20 de março de 2017
- ↑ Miot, Hélio Amante. «Tamanho da amostra em estudos clínicos e experimentais» (PDF). Scientific Electronic Library Online. pp. 275 – 276. Consultado em 23 de março de 2017
- ↑ a b Dodge, Yadolah (2010). The Concise Encyclopaedia of Statistics. New York: Springer. p. 508 – 509. 622 páginas
- ↑ Dodge, Yadolah (2010). The Concise Encyclopaedia of Statistics. New York: Springer. p. 472. 622 páginas
- ↑ Vessereau, André (1976). La Statistique. Paris: Presses Universitaires de France. p. 56. 128 páginas
- ↑ a b c d Ahn, Sangtae; Fessler, Jeffrey A (24 de junho de 2003). «Standard Errors of Mean, Variance, and Standard Deviation Estimators» (PDF). The University of Michigan. p. 1. Consultado em 23 de março de 2017
- ↑ a b Pires, Cesaltina. «Medidas de dispersão e assimetria» (PDF). Universidade de Évora. p. 5. Consultado em 23 de março de 2017
- ↑ a b c Lunet, Nuno; Severo, Milton; Barros, Henrique (2006). «Desvio Padrão ou Erro Padrão» (PDF). Scientific Electronic Library Online. p. 55. Consultado em 23 de março de 2017
- ↑ Devore, Jay L. (2005). Probabilidade e Estatística para Engenharia e Ciências. [S.l.]: Cengage Learning. p. 250 – 251. 692 páginas
- ↑ a b Devore, Jay L. (2005). Estatística e Probabilidade para Engenharia e Ciências. [S.l.]: Cengage Learning. p. 269 – 271. 692 páginas
- ↑ a b Dodge, Yadolah (2010). The Concise Encyclopaedia of Statistics. New York: Springer. p. 71. 622 páginas
- ↑ Anderson, David R.; Sweeney, Dennis J.; Williams, Thomas A. (2010). Statistics – Encyclopaedia Britannica Ultimate Reference Suite. [S.l.: s.n.]
- ↑ a b Deming, W.E. «Quelques Méthodes de Sondage» (PDF). Revue de Statistique Appliquée. 12 (04). Consultado em 24 de janeiro de 2017
- ↑ Cook, John D. (28 de setembro de 2008). «Theoretical Explanation for Numerical Results». John D. Cook. Consultado em 24 de janeiro de 2017
- ↑ Cook, John D. (26 de setembro de 2008). «Comparing Three Methods of Computing Standard Deviation». John D. Cook. Consultado em 24 de janeiro de 2017
- ↑ a b Welford, B. P. «Note on a Method for Calculating Corrected Sums of Squares and Produc» (PDF). Technometrics. 04 (03). Consultado em 24 de janeiro de 2017. Arquivado do original (PDF) em 2 de fevereiro de 2017
- ↑ Cook, John D. «Accurately Computing Running Variance». John D. Cook. Consultado em 24 de janeiro de 2017
- ↑ Yamartino, R. J. (1884). «A Comparison of Several Single–Pass Estimators of the Standard Deviation of Wind Direction». Journal of Climate and Applied Meteorology. 23: 1362 – 1366. Consultado em 24 de janeiro de 2017
- ↑ Bagot, Mike (2009). «Victorian Urban Wind Resource Assessment» (PDF). Consultado em 24 de janeiro de 2017
- ↑ a b Ferignac, P. (1959). «Contrôle de Réception Quantitatif ou par Mesure» (PDF). Revue de Statistique Appliquée. 07 (02). Consultado em 24 de janeiro de 2017
- ↑ a b Ferignac, P. (1965). «Erreurs de Mesure et Contrôle de la Qualité» (PDF). Revue de Statistique Appliquée. 13 (02). Consultado em 24 de janeiro de 2017
- ↑ Saporta, Gilbert (2006). Probabilités – Analyse des Données et Statistiques. Paris: Éditions Technip. p. 43 – 44. 622 páginas
- ↑ Lunet, Nuno; Severo, Milton; Barros, Henrique. «Desvio Padrão ou Erro Padrão» (PDF)
- ↑ Heuer, Rolf (2012). «Une Fin D'Année Pleine de Suspense». Bulletin Hebdomadaire du CERN. Consultado em 24 de janeiro de 2017
- ↑ LIGO Scientific Collaboration, Virgo Collaboration (2016), «Observation of Gravitational Waves from a Binary Black Hole Merger», Physical Review Letters, 116 (6), PMID 26918975, arXiv:1602.03837
 , doi:10.1103/PhysRevLett.116.061102
, doi:10.1103/PhysRevLett.116.061102
- ↑ Abbott, B. P. (2016). «Observation of Gravitational Waves from a Binary Black Hole Merger». Physical Review Letters. Consultado em 24 de janeiro de 2017
- ↑ «The Higgs Boson». Organização Europeia para a Pesquisa Nuclear (CERN). Consultado em 15 de maio de 2017
- ↑ Meyer, Yves (1986). «Principe D'Incertitude, Bases Hilbertiennes et Algèbres D'Opérateurs» (PDF). Séminaire N. Bourbaki (662): 209 – 223. Consultado em 14 de março de 2017
- ↑ «What is Standard Deviation?». Edu Pristine. 7 de novembro de 2011. Consultado em 24 de janeiro de 2017
- ↑ Fery, P. (2010). «Risque et Calcul Socioéconomique» (PDF). Consultado em 24 de janeiro de 2017
- ↑ Zanini, Francisco; Zani, João (2009). Curso Básico de Finanças. [S.l.]: Elsevier. p. 85 – 86. 176 páginas
- ↑ a b Arruda, Diogo Rafael de. «Análise de Risco e Efeitos da Incerteza na Carteira de Investimentos» (PDF). Universidade Católica de Brasília (UCB). Consultado em 6 de fevereiro de 2017
- ↑ a b «Capítulo 8 – Introdução e Gestão de Risco» (PDF). Instituto Educacional BM&FBovespa. Consultado em 6 de fevereiro de 2017. Arquivado do original (PDF) em 17 de maio de 2017
- ↑ «Nonstationary Models for Time Series». Universidade Humboldt de Berlim. Consultado em 23 de março de 2017. Arquivado do original em 5 de dezembro de 2016
- ↑ Masliah, Maurice R. «Stationarity / Nonstationarity Identification». Universidade de Toronto. Consultado em 23 de março de 2017
- ↑ «Bollinger Bands Introduction:». Bollinger Bands. Consultado em 24 de janeiro de 2017
- ↑ «Análise Técnica: Como Utilizar com Maior Eficiência as Bandas de Bollinger». InfoMoney. 2010. Consultado em 6 de fevereiro de 2016
- ↑ a b Lima, Andressa Garcia; Mota, Maria Aurora Santos da. «COMPARAÇÃO ENTRE A TEMPERATURA DA ÁREA URBANA E DA ÁREA RURAL DO MUNICÍPIO DE VIGIA» (PDF). Universidade federal do Pará. p. 3. Consultado em 15 de março de 2016






![{\displaystyle E[X]=\mu }](https://wikimedia.org/api/rest_v1/media/math/render/svg/51ed977b56d8e513d9eb92193de5454ac545231e)

![{\displaystyle {\begin{aligned}\sigma &:={\sqrt {{\rm {Var}}[X]}}={\sqrt {\operatorname {E} [(X-\mu )^{2}]}}\\&={\sqrt {\operatorname {E} [X^{2}]+\operatorname {E} [-2\mu X]+\operatorname {E} [\mu ^{2}]}}&={\sqrt {\operatorname {E} [X^{2}]-2\mu \operatorname {E} [X]+\mu ^{2}}}\\&={\sqrt {\operatorname {E} [X^{2}]-2\mu ^{2}+\mu ^{2}}}&={\sqrt {\operatorname {E} [X^{2}]-\mu ^{2}}}\\&={\sqrt {\operatorname {E} [X^{2}]-(\operatorname {E} [X])^{2}}}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3e70141dabad145092efa60e563a9767b22aded0)



![{\displaystyle \mu ={\rm {E}}[X]={\frac {1}{N}}\sum _{i=1}^{N}x_{i}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/daabb09a60a41a0dd98f1983ef0b39987e5c0553)










![{\displaystyle \mu ={\rm {E}}[X]=\int _{\mathbb {R} }x\,p(x)\,{\rm {d}}x}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fd168f2ddbebe3d83770ae3840b773f012beccbd)


![{\displaystyle {\bigl [}(\exp(\sigma ^{2})-1)\exp(2\mu +\sigma ^{2}){\bigr ]}^{\frac {1}{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1cfa212d05a4dbe07ef0221f80c0e317bdef89f2)











![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)
































![{\displaystyle E[Z^{3}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/853013c7d820de552fcfa0a60875ab8f6d8c938d)
![{\displaystyle E[Z^{4}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/86ca93d841dba522e9a2cfd5c3dc01a3c150f0d1)

![{\displaystyle \operatorname {cov} (X,Y)=E[(X-E[X])\,(Y-E[Y])]={E}[XY]-E[X]E[Y]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cbe3fe09b0d74739c45db3ce2052e7f5ae62f41a)


![{\displaystyle [-1,+1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/daa72f1a806823ec94fda7922597b19cbda684f4)































![{\displaystyle x={\frac {1}{2}}\left[1+\operatorname {erf} \left({\frac {x-\mu }{\sigma {\sqrt {2}}}}\right)\right]={\frac {1}{2}}\left[1+\operatorname {erf} \left({\frac {z}{\sqrt {2}}}\right)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/92a80077c1c5100697c8e560d88d846ebffd3040)
































































![{\displaystyle E[{\hat {\theta }}]-\theta }](https://wikimedia.org/api/rest_v1/media/math/render/svg/6261afc63ac940d8c4be5d8c2d44b755d87923ec)
![{\displaystyle E[{\hat {\theta }}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4f4d1a469bf57194f821b5e64dd5aa4a8134a3c3)


































































































![{\displaystyle [m-1,\!96\,\sigma \,;\,m+1,\!96\,\sigma ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/da55cd8849fdf4a35ecd1febbb84b1aae1343c57)
![{\displaystyle [m-\,\sigma \,;\,m+\,\sigma ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6b45884534989d6d126b63a5b0de654d3c73cac3)
![{\displaystyle ([-2\sigma ,+2\sigma ]13,6+34,1+34,1+13,6)=95,4\%}](https://wikimedia.org/api/rest_v1/media/math/render/svg/92f760eabf9b907be4d1a87408b1b5d2c3c82c1a)
![{\displaystyle ([-3\sigma ,+3\sigma ]2,1+13,6+34,1+34,1+13,6+2,1)=99,6\%}](https://wikimedia.org/api/rest_v1/media/math/render/svg/579d9a9ac400a9652e61d44a7e31ab6c065e3ea6)

