Intervalo de confiança
| Estatística |
|---|
 |
Em estatística, intervalo de confiança (IC) é um tipo de estimativa por intervalo de um parâmetro populacional desconhecido. Introduzido na estatística por Jerzy Neyman em 1937,[1] é um intervalo observado (calculado a partir de observações) que pode variar de amostra para amostra e que com dada frequência (nível de confiança) inclui o parâmetro de interesse real não observável.[2][3]
Como os dados observados são amostras aleatórias da população, o intervalo de confiança construído a partir dos dados também é aleatório.[4] Entretanto, o intervalo de confiança calculado a partir de uma amostra particular não inclui necessariamente o valor real do parâmetro. Quando se tem 99% de confiança de que o valor real do parâmetro está no intervalo de confiança, significa que 99% dos intervalos de confiança observados têm o valor real do parâmetro. Tomando-se qualquer amostra particular, o parâmetro populacional desconhecido pode ou não pode estar no intervalo de confiança observado.[5]
O nível de confiança é a frequência com a qual o intervalo observado contém o parâmetro real de interesse quando o experimento é repetido várias vezes. Em outras palavras, o nível de confiança seria a proporção de intervalos de confiança construídos em experimentos separados da mesma população e com o mesmo procedimento que contém o parâmetro de interesse real.[1][6][7] Em geral, refere-se a intervalo de confiança quando as duas extremidades de estimativa intervalar são finitas. Entretanto, refere-se a limiares superiores/inferiores de confiança quando uma das extremidades é infinita. O nível de confiança de 99% significa que 99% dos intervalos de confiança construídos a partir das amostras aleatórias contêm o parâmetro real. O nível de confiança desejado é determinado pelo pesquisador, não pelos dados. Se um teste de hipótese for realizado, o nível de confiança é o complemento do nível de significância. Isto é, um intervalo de confiança de 95% reflete um nível de significância de 0,05.[8]
Os intervalos de confiança são tipicamente estabelecidos no nível de confiança de 95%.[9] Entretanto, quando apresentados graficamente os intervalos de confiança podem ser mostrados em vários níveis de confiança como 90%, 95% e 99%.[10] Certos fatores podem afetar o tamanho do intervalo de confiança, incluindo o tamanho da amostra, o nível de confiança e a variabilidade da população. Um tamanho de amostra maior normalmente levará a uma estimativa melhor do parâmetro populacional.[11] O intervalo de confiança contém os valores do parâmetro que quando testados não devem ser rejeitados com a mesma amostra. O intervalo de confiança de diferença do parâmetro entre duas populações que não contém 0 implica uma diferença significativa do mesmo parâmetro entre as populações.[12]
História[editar | editar código-fonte]

O intervalo de confiança foi introduzido por Jerzy Neyman (1894–1981). Formado em matemática pelo Instituto de Tecnologia de Kharkov, Neyman demonstrou interesse pela estatística desde que era estudante do probabilista russo Sergey Natanovich Bernstein. O interesse pela estatística levou Neyman a estudar com importantes matemáticos como Karl Pearson, Émile Borel, Henri Lebesgue, Paul Pierre Lévy e Jacques Hadamard.[13]
Em 1926, Neyman começou a parceria com Egon Sharpe Pearson na University College London. Neyman ingressou na University College para estudar com Karl Pearson, pai de Egon Sharpe Pearson. Neyman e Pearson desenvolveram vários conceitos sobre testes de significância de prova de hipóteses.[13]
Em 1934 Neyman retomou os estudos sobre a estimação intervalar, assunto ao qual tinha se dedicado desde 1930.[13][14] Foi quando surgiu a teoria do intervalos de confiança, publicada no apêndice do artigo On the Two Different Aspects of the Representative Method: the Method of Stratified Sampling and the Method of Purposive Selection.[15]
Nota-se que desde que se tornou doutor em matemática pela Universidade de Varsóvia em 1923, Neyman também cooperou com vários institutos de agricultura e supervisionou vários estudantes de doutorado. Dentre eles W. Pytkowski, que questionou como caracterizar não dogmaticamente a precisão de um coeficiente de regressão estimado, o que ajudou Neyman a elaborar a teoria do intervalo de confiança.[14]
Em 1970 Neyman recebeu um título honorário pelos seus estudos em Londres que citam o intervalo de confiança:[16]
| “ | Durante os anos 1934–1938, Neyman fez quatro contribuições fundamentais para a ciência da estatística. Cada uma delas teria sido suficiente para estabelecer uma reputação internacional, tanto pelos seus efeitos imediatos quanto para o ímpeto que as novas ideias e métodos tiveram no pensamento de pessoas mais jovens e mais velhas. Ele apresentou a teoria de intervalos de confiança, cuja importância em teoria estatística e análise de dados não pode ser enfatizada demais. Suas contribuições para a teoria das distribuições contagiosas ainda é de grande utilidade na interpretação de dados biológicos. Seu trabalho sobre amostragem estratificada abriu caminho para uma teoria estatística, entre outros, para Gallup Poll. O seu [trabalho] e o [trabalho de] Fisher, cada qual com um modelo diferente para os experimentos randomizados, levaram para um novo campo de experimentação muito usado na agricultura, na biologia, na medicina e nas ciências físicas. | ” |
Em 1938, Neyman mudou-se para os Estados Unidos e tornou-se professor no Departamento de Matemática da Universidade da Califórnia. Hoje Neyman é considerado um dos fundadores da estatística moderna, com teorias sobre probabilidades, teste de hipóteses, teste de qui-quadrado, entre outros.[13]
Definição informal[editar | editar código-fonte]
Um intervalo de confiança para um parâmetro populacional é um intervalo com uma proporção associada gerada por uma amostra aleatória de uma população subjacente, de tal forma que se o experimento for repetido várias vezes e o intervalo de confiança for recalculado para cada experimento com mesmo procedimento, uma proporção dos intervalos de confiança conteria o parâmetro estatístico em questão.[17]
Os intervalos de confiança são usados para indicar a confiabilidade de uma estimativa. Por exemplo, o intervalo de confiança pode ser usado para descrever o quão confiáveis são os resultados de uma pesquisa (uma pesquisa com intervalo de confiança menor é mais confiável que uma pesquisa com intervalo de confiança maior). O intervalo de confiança com nível de confiança de 95% é o mais comum e significa que o resultado está dentro do intervalo de 95 dos 100 estudos hipoteticamente realizados (a leitura correta é que o resultado está dentro do intervalo de confiança em 95 das 100 amostras realizadas).[8]
Os intervalos de confiança são a forma predominante de estimativa por intervalo, que pode ser contrastada com estimativa pontual corresponde ao valor único dado como a estimativa de um parâmetro da população de interesse. A estimativa por intervalo especifica um intervalo dentro do qual o parâmetro deve estar. Os intervalos de confiança são comumente reportados como tabelas ou gráficos juntamente com estimativas pontuais do mesmo parâmetro para mostrar a confiabilidade das estimativas.[18]
Por exemplo, de acordo com uma pesquisa sobre intenção de votos, 40% dos entrevistados pretendem votar em um certo partido. É possível calcular um intervalo de confiança de 99% para a proporção de toda a população com a mesma intenção de voto, que pode ficar entre 30% e 50%. Também é possível calcular um intervalo de confiança de 90% para a proporção de toda a população com a mesma intenção de voto, que neste caso pode ficar entre 37% e 43%. Um importante fator que determina o comprimento de um intervalo de confiança é o tamanho da amostra usado no processo de estimativa. Por exemplo, o número de pessoas que participaram da pesquisa.

Baseando-se na imagem ao lado, é um equívoco supor que duas quantidades cujos intervalos de confiança de 95% se sobreponham (barras à direita) sejam significativamente diferentes ao nível de 5%.[19]
O intervalo de confiança em probabilidade frequencista tem papel semelhante ao intervalo de credibilidade em estatística bayesiana. O intervalo de confiança também tem relações com outros temas estatísticos como teste de significância, regiões de confiança e confiança de banda.[20] O tamanho do intervalo de confiança pode ser influenciado pelo tamanho da amostra, pelo nível de confiança e por variações diversas. Lembrando que uma amostra maior conduzirá a uma estimativa melhor do parâmetro analisado.[11]
Interpretação[editar | editar código-fonte]
Pode-se afirmar que se forem construídos um grande número de intervalos de confiança nestas condições aproximadamente destes intervalos de confiança conterão o valor real de parâmetro (permanece desconhecido). Isto é esta a ideia traduzida por confiança.[21]
Em inferência frequencista, várias interpretações do intervalo de confiança podem ser dadas tomando-se o exemplo do intervalo de confiança de 90%.
- O intervalo de confiança pode ser expresso em termos de amostras ou amostras repetidas (replicação). De acordo com Cox e Hintley, "se o procedimento for repetido para várias amostras, a fração dos intervalos de confiança calculados que pode variar de amostra para amostra e inclui o parâmetro real da população tende a 90%".[7]
- O intervalo de confiança pode ser expresso em termos de uma única amostra. Segundo Neyman, "há probabilidade de 90% do intervalo de confiança de algum experimento futuro incluir o valor real do parâmetro da população." Nota-se que isto é uma afirmação estatística sobre o intervalo de confiança, não sobre o parâmetro da população.[1] Isto considera a probabilidade associada ao intervalo de confiança a partir de um ponto de vista pré-experimental, no mesmo contexto em que os argumentos para a alocação aleatória de tratamentos para itens de estudo são feitos. O pesquisador antes de realizar o experimento real determina a forma pela qual ele pretende calcular o intervalo de confiança, e assim o intervalo de confiança que será calculado tem uma chance de 90% de cobrir o valor real desconhecido. Isto é muito similar à interpretação da replicação acima, exceto por evitar basear-se nas repetições hipotéticas de um procedimento de amostragem que não pode ser repetido em nenhum sentido significativo.[1]
- Para Cox e Hintley, "o intervalo de confiança representa os valores para um parâmetro da população para o qual a diferença entre o parâmetro e a estimativa observados não é estatisticamente significante no nível de confiança de 10%." Isto está relacionado a uma forma particular pela qual o intervalo de confiança pode ser construído. Por exemplo, em casos em que a construção do intervalo de confiança baseia-se na estimativa do parâmetro.[22]
Em cada interpretação, aplica-se o seguinte: se o valor real de um parâmetro está fora do intervalo de confiança de 90% uma vez que ele foi calculado, então este evento ocorreu com a probabilidade de 10% (ou menos) de acontecer por acaso.[23]
Erro de interpretação[editar | editar código-fonte]
Intervalos de confiança são frequentemente confundidos. Estudos publicados têm mostrado que mesmo cientistas profissionais frequentemente os interpretam erroneamente.[24][25][26]
- Um intervalo de confiança de 95% não significa que para um dado intervalo calculado a partir de dados da amostra há a probabilidade de 95% do parâmetro da população estar dentro do intervalo.[24] Uma vez que um experimento é realizado e um intervalo é calculado, este intervalo pode cobrir ou não cobrir o valor do parâmetro. Não é mais uma questão de probabilidade. A probabilidade de 95% está relacionada à confiabilidade do procedimento de estimativa, não a um intervalo específico calculado.[27]
Neyman afirma em seu trabalho original:[1]
| “ | Note que na descrição acima, as afirmações sobre probabilidade referem–se aos problemas de estimativa com os quais os estatísticos estarão preocupados no futuro. De fato, tenho dito repetidamente que a frequência de resultados corretos tenderá a α. Agora considere o caso quando a amostra já está desenhada e os cálculos já estão dados [limites particulares]. Podemos afirmar que neste caso particular a probabilidade de o valor real [ficar entre esses limites] é igual a α? A resposta é obviamente negativa. O parâmetro é uma constante desconhecida e nenhuma afirmação sobre probabilidade referente ao seu valor pode ser feita (...) | ” |
- Deborah Mayo expande o assunto:[28]
| “ | Deve ser ressaltado, entretanto, que tendo visto o valor dos dado, a teoria de Neyman–Pearson nunca permite concluir que o intervalo de confiança específico formado cobre o valor real 0 com probabilidade de 100% (1 − α) ou grau de confiança de 100% (1 − α). A observação de Seidenfeld parece enraizada em um desejo (não incomum) dos intervalos de confiança de Neyman–Pearson fornecerem algo que não podem legitimamente oferecer. Isto é, uma medida do grau de probabilidade, crença ou suporte que o valor de um parâmetro desconhecido estão em um intervalo específico. Segundo Savage (1962), a probabilidade de um parâmetro estar em um intervalo específico pode referir–se como uma medida de precisão final. Enquanto a medida de precisão final pode parecer desejável e os níveis de confiança são frequentemente (erroneamente) interpretados como fornecedores de tais medidas, tal interpretação não é justificada. É certo que essa interpretação errada é encorajada pela palavra confiança. | ” |
- Um intervalo de confiança de 95% não significa que 95% dos dados da amostra estejam dentro do intervalo.[5]
- Um intervalo de confiança não é um intervalo de valores plausíveis para o parâmetro amostral, embora possa ser entendido como uma estimativa de valores plausíveis para o parâmetro da população.[29]
- Um intervalo de confiança específico de 95% calculado a partir de uma experiência não significa que há uma probabilidade de 95% de uma estimativa de parâmetro amostral calculada a partir da repetição de uma mesma experiência ficar dentro deste intervalo.[30]
Definição formal[editar | editar código-fonte]
Seja uma amostra aleatória de uma distribuição de probabilidade com parâmetro estatístico , que é a quantidade a ser estimada. Seja as quantidades (parâmetros) que não são de interesse imediato. Um intervalo de confiança para o parâmetro , com nível de confiança ou coeficiente de confiança , é um intervalo com pontos aleatórios , determinado pelo par de variáveis aleatórias e com a propriedade para todo [18]
As quantidades que não são de interesse imediato são chamadas parâmetros de incômodo (a teoria estatística ainda precisa encontrar alguma forma de lidar com eles).[31] O número , com valores típicos próximos, mas não maiores que 1, são às vezes dados na forma ou como a porcentagem , em que é um pequeno número não negativo próximo de 0.[18]
indica a distribuição de probabilidade de caracterizado por . Uma parte importante desta especificação é que o intervalo aleatório cobre o valor desconhecido com grande probabilidade independente do valor real de .[3] Nota-se que não precisa referir-se a uma dada família de distribuições explicitamente parametrizada, embora a propriedade geralmente refira-se a ela. Assim como a amostra aleatória teoricamente corresponde a outras possíveis realizações a partir da mesma população ou a partir da mesma versão da realidade, os parâmetros indicam que é necessário considerar outras versões da realidade nas quais a distribuição de pode ter diferentes características.[18]
Em situações específicas, quando é o resultado da amostra , o intervalo também refere-se como o intervalo de confiança para . Nota-se que não é mais possível afirmar que o intervalo observado tem probabilidade de conter o parâmetro . Este intervalo observado é apenas uma realização dos todos os intervalos possíveis, para os quais se sustenta a probabilidade.[18]
Intervalos de confiança aproximados[editar | editar código-fonte]
Em muitas aplicações, os intervalos de confiança que possuem exatamente o nível de confiança requerido são difíceis de construir. Porém na prática intervalos úteis ainda podem ser encontrados. A regra para construir o intervalo pode ser aceita fornecendo um intervalo de confiança no nível se para todo para um nível aceitável de aproximação. De outro modo, alguns autores simplesmente requerem que para todo que é útil se as probabilidades forem apenas parcialmente identificadas ou imprecisas.[32]
Propriedades desejáveis[editar | editar código-fonte]
Quando aplicados procedimentos estatísticos "padrão", geralmente haverá formas padronizadas para construir intervalos de confiança. Os intervalos de confiança serão construídos de modo a satisfazer certas propriedades desejáveis, que se manterão dada que as suposições sobre o procedimentos são verdadeiras. Estas propriedades desejáveis podem ser descritas como validade, otimização e invariância.[33] A validade é a propriedade mais importante, seguida pela otimização. A invariância pode ser considerada a propriedade do método de derivação em vez da regra do construção do intervalo de confiança. Quando aplicados procedimentos estatísticos "não padrão", as mesmas propriedades desejáveis seriam procuradas.[34]
- Validade: Significa que a probabilidade de cobertura nominal (nível de confiança) do intervalo de confiança deve manter-se exatamente ou com uma boa aproximação.[34]
- Otimização: Significa que a regra para construir o intervalo de confiança dever fazer o máximo de uso possível da informação do conjunto de dados. Lembra-se de que é possível descartar metade do conjunto de dados e ainda ser possível fazer um intervalo de confiança válido. Uma forma de avaliar a otimização é por meio do comprimento do intervalo, para que então a regra para a construção do intervalo de confiança seja melhor julgada se ela leva para intervalos cujos comprimento são tipicamente menores.[34]
- Invariância: Em muitas aplicações, a quantidade a ser estimada pode não ser bem definida como tal. Por exemplo, uma pesquisa pode resultar em uma estimativa da renda média da população e pode igualmente fornecer a estimativa do logaritmo da renda média dado que é uma escala comum para representar resultados gráficos. Seria desejável que o método usado para construir o intervalo de confiança para a renda média destes resultados equivalentes quando aplicados à construção do intervalo de confiança para o logaritmo da renda média. Especificamente os valores nas extremidades dos últimos intervalos seriam os logaritmos dos valores nas extremidades do intervalo anterior.[34]
Métodos de derivação[editar | editar código-fonte]
Para outros tipos de aplicações menos comuns, existem várias rotas que poderiam ser tomadas para derivar uma regra para a construção do intervalo de confiança. Normalmente uma regra para a construção de intervalos de confiança está intimamente ligada a uma forma particular de encontrar uma estimativa pontual da quantidade a ser considerada.[35]
Estatísticas descritivas[editar | editar código-fonte]
O uso de estatísticas descritivas está intimamente relacionado com o método dos momentos de construção dos estimadores. Um exemplo simples surge quando a quantidade a ser avaliada é a média, em cujo caso uma estimativa natural é a média amostral. Os argumentos habituais indicam que a variância amostral pode ser utilizada para estimar a variação da média amostral. Um intervalo de confiança sem muitos detalhes para a média verdadeira pode ser construído a partir da média amostral com uma largura, que é um múltiplo da raiz quadrada da variância amostral.[36]
Teoria da probabilidade[editar | editar código-fonte]
Quando as estimativas são construídas usando o princípio da máxima verosimilhança, a teoria para este experimento fornece duas formas de construir o intervalo de confiança. Uma forma é usar o Teorema de Wilks para encontrar todos os possíveis valores de que completam a seguinte restrição .[37] Portanto, a matriz de covariância que maximiza a verosimilhança é dada por [38]
Estimação de equações[editar | editar código-fonte]
A abordagem de estimativa aqui pode ser considerada tanto uma generalização de método de momentos como uma generalização da abordagem de máxima verosimilhança. Há generalizações correspondentes dos resultados da teoria de probabilidade máxima que permitem que os intervalos de confiança a ser construído com base em estimativas derivadas de equações de estimação.[39]
Teste de significância[editar | editar código-fonte]
Se os testes de significância estão disponíveis para os valores gerais de um parâmetro, então os intervalos de confiança podem ser construídos por meio da inclusão na região de confiança a todos os pontos para os quais o teste de significância da hipótese nula com dado valor verdadeiro não é rejeitado com nível de significância de .[40]
Bootstrapping (reamostragem)[editar | editar código-fonte]

Bootstrap é uma amostra de dados com reposição a partir de uma amostra de uma população . Ou seja, considere uma população qualquer de dados como folhas de árvores, neurônios humanos, cardumes de peixes da espécie lambari e etc. Então, a partir de uma população de interesse, para serem realizadas análises estatísticas obtém-se uma amostra , onde é a amostra e cada são os elementos da amostra.[41][42]
A partir da amostra se obtém uma nova amostra de tamanho que se chama reamostragem (amostra Bootstrap). A amostra Bootstrap de é , onde cada são escolhas aleatórias da amostra . Como os elementos de são escolhidos de forma aleatória de , encontram-se outros desvios padrões da mesma amostra permitindo uma confiabilidade maior na análise o que faz reduzir desvios (erros) na análise. Além disso, a amostra de Bootstrap quantifica a incerteza do cálculo dos erros padrões e intervalo de confiança.[42]
A amostra Bootstrap também é usada para situações em que as suposições de distribuição dos métodos são incertos ou violados. O método de reamostragem permite a construção de intervalos de confiança ou intervalos de predição. A distribuição dos dados observados e as correlações internas são utilizados como o substituto para as correlações entre a população mais ampla. Portanto, a amostra Bootstrap não precisa ser grande ou com característica normais, gera menos suposições e útil para os casos em que não há distribuição de amostra finita.[43]
Exemplo teórico[editar | editar código-fonte]
Intervalo de confiança para a média de uma população [editar | editar código-fonte]
Seja uma população de média e desvio padrão , da qual se toma amostras de elementos. Cada uma das amostras tem média , sendo que a média de todas as amostras significativas coincide com a média da população .[44][45][46] Se o tamanho da amostra for suficientemente grande, a distribuição amostral segue praticamente uma distribuição normal (distribuição de Gauss) com média e desvio padrão . Isto é representado como . Padronizando, tem-se .[47]
Com , pode-se calcular um intervalo de confiança dentro do qual pode conter uma determinada porcentagem de observações. É possível encontrar e , tal que , em que é o porcentual desejado. Com , . Nesta distribuição normal, pode-se calcular o intervalo de confiança em que a população significativa apenas pode ser encontrada se uma amostra conhecida com média tiver uma certa confiança. Normalmente, os valores entre 95% e 99% são comuns. Estes valores serão chamados de . Isto exige o cálculo de ou do valor crítico junto com sua distribuição oposta . [44][45][46]
Estes pontos definem a probabilidade do intervalo de tempo como mostra a figura a seguir.

Este ponto é o número tal que . Para a versão padronizada, assegura-se . Assim, . Fazendo possíveis operações de compensação, , no qual o intervalo de confiança obtido é. Nota-se que o intervalo de confiança é dado pela média amostral . O erro padrão é . Se não for conhecido e for muito grande, então pode ser usado o intervalo , em que é o desvio padrão amostral. Mas quando não for muito grande, prossegue-se com outro método.[44][45][46]
Seja , , em que é a média amostral e é a variância amostral. Então, sabe-se que tem distribuição t de Student com graus de liberdade (como a distribuição não depende dos valores dos parâmetros não observáveis e , é uma quantidade essencial).[48]
Por exemplo, a construção do intervalo de confiança de 95% para . Seja o 97,5 percentil da distribuição ou . Há 2,5% de chance de ser menor que e 2,5% de chance de ser maior que . Então, a probabilidade de estar entre e é 95%. Consequentemente, , com intervalo de confiança teórico (estocástico) de 95% para . Depois de observar a amostra, encontra-se valores para e para , a partir dos quais calcula-se o intervalo de confiança com números fixos como extremidades, sobre os quais não pode-se afirmar que há certa probabilidade de conter o parâmetro e que está ou não está neste intervalo.[44][45][46]
Intervalo de confiança para uma proporção [editar | editar código-fonte]
O intervalo de confiança para a estimativa de uma proporção de uma amostra de tamanho para um nível de confiança quando há reposição de uma população infinita é. A demonstração destas fórmulas envolvem o teorema central do limite e a abordagem de um binômio normal. Quando não há reposição, tem-se, .[49]
Exemplos práticos[editar | editar código-fonte]
Consumo médio de bebida em uma festa[editar | editar código-fonte]
Seja um buffet que tenha realizado 500 festas, desde festas pequenas com 10 convidados até festas grandes com 1 000 convidados. Medindo o consumo médio de bebida por pessoa em todas as festas, percebe-se que cada pessoa bebe em média 200 mL com desvio padrão de 50 mL. Deseja-se fazer uma festa com o mínimo possível de bebida para desperdiçar menos e lucrar mais. O que fazer? Compra-se 200 mL de bebida para cada pessoa? Para não correr o risco de faltar bebida e desagradar o cliente, resolve-se comprar uma quantidade pouco superior à média: média mais duas vezes desvio padrão, que é 300 mL de bebida por pessoa. Supondo que o próximo evento seja para 20 convidados. Como a quantidade considerada é de 300 mL de bebida por pessoa, decide-se comprar 6 litros de bebidas. Mas será que a quantidade é suficiente? Quais as chances da média de consumo de bebida por pessoa superar 300 mL?[50]
Para calcular a probabilidade, é preciso saber a média de consumo de bebida por pessoa e o desvio padrão no evento para 20 convidados para criar o gráfico da distribuição normal. Como não tem-se os valores porque a festa ainda não aconteceu, a solução é simular uma curva normal a partir dos dados históricos. Como a média histórica do consumo de bebida por pessoa e a média do evento serão muito próximos, o valor será o mesmo (200 mL). Embora o desvio padrão não possa ser o mesmo, sabe-se que o desvio padrão amostral é igual ao desvio padrão da população dividido pela raiz quadrada do tamanho da amostra. Então, o desvio padrão da curva normal calculado a partir dos dados históricos será igual a .[50]
Com os valores da média amostral (200 mL) e do desvio padrão (11,18034 mL), tem-se a curva normal simulada para a próxima festa. Para saber a probabilidade do consumo de bebida por pessoa ser superior a 300 mL, basta subtrair a média amostral (200 mL) do consumo de bebida por pessoa (300 mL) e dividir pelo desvio padrão simulado (11,18034 mL), obtendo-se . Consultando-se qualquer tabela de distribuição normal acumulada em livros ou na Internet, encontra-se que para a probabilidade é 0,7881. Como quer-se calcular a probabilidade da média do consumo de bebida por pessoa ser superior a 300 mL, é preciso subtrair 0,7881 de 1. Portanto, a probabilidade do consumo de bebida por pessoa ser superior a 300 mL em um evento para 20 convidados é de 0,2119 ou de 21,19%.[50]
Máquina de sorvete[editar | editar código-fonte]
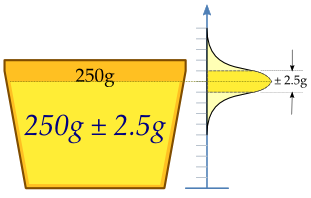
Uma máquina é ajustada para despejar 250 gramas de sorvete. Como a máquina não pode encher cada copo com exatamente 250 gramas, o conteúdo adicionado apresenta variação e é considerado uma variável aleatória . Supõe-se que a variação é ajustada para uma distribuição normal em torno da porcentagem média desejada de 250 gramas com desvio padrão de 2,5 gramas. Para determinar se a máquina está devidamente calibrada, uma amostra aleatória 25 copos é pesada. Os pesos resultantes são , uma amostra aleatória de .Para média , basta fornecer uma estimativa. A estimativa apropriada é a média amostral . Os pesos reais da amostra têm média .[51]
Considerando-se outra amostra de 25 copos, pode-se esperar encontrar valores médios como 250,4 gramas ou 251,1 gramas. Entretanto, o valor da média amostral de 280 gramas seria raro se o conteúdo médio dos copos fosse de fato próximo de 250 gramas. Há um intervalo em torno do valor observado de 250 gramas da média amostral dentro de cada copo. Se toda média da população realmente tomar o valor neste intervalo, o dado observado não será considerado particularmente incomum. Este intervalo é chamado intervalo de confiança para o parâmetro . Para calcular este intervalo de confiança, é preciso calcular as extremidades do intervalo a partir da amostra. São funções estatísticas da amostra e, portanto, são variáveis aleatórias. No exemplo, pode-se determinar as extremidades considerando que a média amostral da amostra normalmente distribuída também é normalmente distribuída com a mesma expectativa e com desvio padrão de [50]
Para padronização, a variável aleatória é obtida por .[52]
Tomando-se , tem-se . O número a partir da seguinte função de distribuição cumulativa ou a função de distribuição cumulativa é
.[53]
Então, obtém-se
.[53]
Em outras palavras, a extremidade inferior do intervalo de confiança é 95% é e a extremidade superior do intervalo de confiança é 95% é .
Com os valores do exemplo, o intervalo de confiança é
.[53]
Observações[editar | editar código-fonte]
Um intervalo de confiança aproximado para a média da população pode ser construído para variáveis aleatórias que não são normalmente distribuídas na população, permanecendo no teorema central do limite se os tamanhos e as contagens das amostras forem suficientemente grandes. As fórmulas são idênticas ao caso acima (em que a média amostral é na verdade normalmente distribuída em relação à média da população). A aproximação será muito boa com apenas algumas dúzias de observações da amostra se a distribuição de probabilidade da variável aleatória não for muito diferente da distribuição normal (por exemplo, a função cumulativa de distribuição não tem nenhuma descontinuidade e sua distorção é moderada).[54][55]
Um tipo de média amostral é a média de uma variável dummy, que toma o valor "1" como verdadeiro e o valor "0" como falso. A média desta variável é igual a proporção em tem a variável igual a 1 (na população e em qualquer amostra). Esta é uma propriedade útil das variáveis dummy, especialmente para os testes de hipóteses. Para aplicar o teorema central do limite, é preciso usar uma amostra suficientemente grande. Uma regra de ouro é que deve-se ver pelo menos 5 casos, nos quais o indicador é 1, e pelo menos 5 casos, nos quais o indicador é 0. Intervalos de confiança construídos usando a fórmula acima podem incluir números negativos ou números maiores que 1, mas as proporções obviamente não podem ser negativas ou exceder 1. Proporções das amostras também podem tomar apenas números infinitos de valores, então o teorema central do limite e a distribuição normal não são as melhores ferramentas para construir um intervalo de confiança.[56]
Interpretação[editar | editar código-fonte]

Com probabilidade 0,95, encontra-se um intervalo de confiança no qual o valor do parâmetro estará entre as extremidades estocásticas e . Isto não significa que há probabilidade de 95% do valor do parâmetro estar no intervalo obtido usando o valor computado da média amostral . De modo contrário, toda vez que as medidas repetem-se, haverá outro valor para a média da amostra. Em 95% dos casos, estará entre as extremidades calculadas a partir da média. O intervalo de confiança real é calculado, inserindo as massas medidas na fórmula. O intervalo de confiança de 95% torna-se . Em outras palavras, o intervalo de confiança de 95% está entre a extremidade inferior de 249,22 gramas e a extremidade superior de 251,18 gramas. Como o valor desejado 250 de está dentro do intervalo de confiança resultantes, não há razão para acreditar que a máquina está calibrada de maneira errada.[57]
O intervalo calculado tem extremidades fixas, em que pode ou não pode estar entre elas. Portanto, este evento tem probabilidade 0 ou 1. Não é possível afirmar que com probabilidade o parâmetro está no intervalo de confiança. Pela repetição, em dos casos está no intervalo calculado. Em dos casos, isto não acontece. Porém, não é possível saber em quais casos isto acontece. É por isso que em vez de usar o termo probabilidade é possível afirmar que com nível de confiança está no intervalo de confiança. A imagem mostra 50 realizações de intervalos de confiança para a média de uma dada população. Se uma realização for aleatoriamente escolhida, a probabilidade é de 95% de escolher um intervalo que contenha o parâmetro. Entretanto, pode-se dar azar e escolher o intervalo errado. Nunca se sabe.[57]
Margem de erro[editar | editar código-fonte]
A margem de erro para uma estatística particular geralmente é definida como o raio ou a metade da largura do intervalo de confiança para a mesma estatística.[58][59] Portanto, para determinar o erro de um intervalo de confiança ao estimar a média de uma população qualquer e a partir da média da população . Tem-se[60]
, em que .[60]
Pode-se utilizar a média amostral como estimador para gerar o erro quadrático médio (EQM), definido como .[61] Isto é, ao considerar o parâmetro da distribuição da variável aleatória pelo estimador , quando a amostra é , tem-se o EQM do estimador .[61]
Relação com outros tópicos estatísticos[editar | editar código-fonte]
Teste de hipótese estatístico[editar | editar código-fonte]
Intervalos de confiança são intimamente ligados ao teste de significância estatístico. Por exemplo, se para algum parâmetro estimado quer testar da hipótese nula contra a alternativa , então este teste pode ser realizado determinando se o intervalo de confiança para contém 0.[62] Em termos mais gerais, dada a disponibilidade de um procedimento de teste de hipótese que pode testar a hipótese nula contra a alternativa para qualquer valor de , então o intervalo de confiança com nível de confiança pode ser definido como contendo qualquer número para o qual a hipótese numa correspondente não é rejeitada no nível de significância .[63]
Se a estimativa dos dois parâmetros (parâmetros, os valores médios de uma variável em dois grupos independentes) tem intervalos de confiança, então a diferença entre os dois valores é mais significante que a indicada pelos valores individuais de .[30] Então, este teste é muito conservador e pode levar a um resultado que é mais significante que os valores individuais de poderiam indicar. Se dois intervalos de confiança se sobrepõem, as duas médias ainda podem ser significantemente diferentes.[19][64][65] Por conseguinte, consistente com o teste qui-quadrado de Manter Haenszel, é uma correção proposta pela qual reduz-se os limites de erro para duas médias multiplicando-as para raiz quadrada de 0,5 (0,707107) antes de fazer a comparação.[66]
Enquanto as formulações das noções de intervalos de confiança e de testes de hipótese estatísticos são distintos, eles são em algum sentido relacionados e em alguma medida complementares. Enquanto nem todos os intervalos de confiança são construídos desta maneira, uma abordagem genérica proposta para construir intervalos de confiança é definir um intervalo de confiança de para consistir todos estes para quais o teste de hipótese não é rejeitado no nível de significância de .[67] Tal abordagem nem sempre pode estar disponível uma vez que pressupõe a disponibilidade prática de um teste de significância apropriado. Naturalmente, quaisquer suposições necessárias para o teste de significância seriam transferidas para os intervalos de confiança.[68]
Pode ser conveniente fazer a conveniência geral que os valores dos parâmetros dentro do intervalo de confiança são equivalentes para aqueles valores que não seriam rejeitados pelo teste de hipótese, mas isto não seria indicado. Em muitas circunstâncias, os intervalos de confiança citados são apenas aproximadamente válidos, talvez derivados de mais ou menos o dobro do erro padrão e as implicações disto para o teste de hipótese supostamente corresponde geralmente não são conhecidas.[68] Nota-se que o intervalo de confiança para um parâmetro não é o mesmo que a região de aceitação de um teste para este parâmetro, como às vezes se pensa. O intervalo de confiança é parte do espaço do parâmetro, independente se a região de aceitação é parte do espaço da amostra. Pela mesma razão o nível de confiança não é o mesmo que a probabilidade complementar do nível de significância.[69]
Região de confiança[editar | editar código-fonte]
As regiões de confiança generalizam o conceito de intervalo de confiança para lidar com múltiplas quantidades. Tais regiões podem indicar não apenas a extensão dos prováveis erros de amostragem, mas também podem revelar se (por exemplo) é o caso de se a estimativa para uma quantidade não for confiável, então outra também não deve ser confiável.[70]
Faixa de confiança[editar | editar código-fonte]
Uma faixa de confiança é usada em análise estatística para representar a incerteza em uma estimativa de uma curva ou uma função baseada em dados limitados ou ruidosos. Similarmente, uma banda de previsão é usada para representar a incerteza sobre o valor de um novo ponto de dado na curva, mas sujeito ao ruído. As faixas de previsão e de confiança são frequentemente usadas como parte da representação gráfica dos resultados da análise de regressão. As faixas de confiança são intimamente relacionadas ao intervalo de confiança, que representam a incerteza em uma estimativa de um único valor numérico.[71] À medida que os intervalos de confiança, pela construção, apenas referem-se a um único ponto, eles são mais estreitos (neste ponto) que a faixa de confiança que deve manter-se simultaneamente em muitos pontos.[72]
Outros métodos de estimativa por intervalo[editar | editar código-fonte]
Os intervalos de confiança são um método de estimativa por intervalo e o método mais usado na estatística frequencista. Um conceito análogo na estatística bayesiana é o intervalo de credibilidade, enquanto um método frequencista alternativo é o intervalo de previsão, que em vez de estimar parâmetro, estima o resultado de amostras futuras (para outras abordagens para expressar a incerteza usando intervalos, ver estimativa por intervalo).[20]
Comparação com intervalos de previsão[editar | editar código-fonte]
Um intervalo de previsão de uma variável aleatória é definido de maneira parecida ao intervalo de confiança para o parâmetro estatístico. Considerando uma variável aleatória , que pode ou não pode ser estatisticamente dependente da amostra aleatória . Então, fornece um intervalo de previsão para o valor a ser observado de se para todo indica a distribuição de probabilidade conjunta das variáveis aleatórias , nas quais estas distribuições dependem dos parâmetros estatísticos .[73][74]
Comparação com intervalos de tolerância[editar | editar código-fonte]
O intervalo de tolerância é um intervalo estatístico tal que os dados da amostra caem neste intervalo com uma certa proporção específica. O intervalo de tolerância delimita um intervalo superior e inferior de uma distribuição. Isto é, a área na qual abrange as características almejadas da distribuição. Mais especificamente, intervalo de tolerância fornece limites dentro de qual uma certa proporção da população cai com um dado nível de confiança .[75] Um intervalo de tolerância baseado em uma amostra é construído, de modo a incluir pelo menos a proporção da população amostral com confiança . Tal intervalo de tolerância geralmente é referido como intervalo de tolerância com conteúdo e cobertura .[76] Um intervalo de tolerância pode ser visto como a versão estatística do intervalo de probabilidade. Intervalos de tolerância unilaterais normais tem uma solução exata em termos de média amostral e variância amostral baseada na distribuição-t não central. Intervalos de tolerância bilaterais normais podem ser obtidos com base na distribuição não central.[77]
Comparação com intervalo bayesiano[editar | editar código-fonte]
Uma estimativa do intervalo bayseano é chamada de "intervalo de credibilidade". Usando muitas das mesmas notações acima, a definição de intervalo de credibilidade para o valor real desconhecido de para um dado é é usado para enfatizar que o valor desconhecido de é tratado como uma variável aleatória.[78] As definições dos dois tipos de intervalo podem ser comparadas como a seguir.
- A definição do intervalo de confiança envolve probabilidades calculadas a partir da distribuição de para um dado (ou condicional a estes valores) e a condição precisa manter-se todos os valores de .[18][20]
- A definição de intervalo de credibilidade envolve probabilidades calculadas a partir da distribuição de condicional aos valores observados de e marginalizada (na média) sobre os valores de , em que esta última quantidade é a variável aleatória correspondente à incerteza sobre os parâmetros de incômodo em .[20][31]
Nota-se que o tratamento dos parâmetros de incômodo acima é geralmente omitido das discussões, comparando a confiança e a credibilidade, mas é marcadamente diferente entre os dois casos. Em alguns casos padrões simples, os intervalos produzidos como os intervalos de confiança e os intervalos de credibilidade a partir do mesmo conjunto de dados podem ser idênticos.[79] Eles são muito diferente se a probabilidade a priori informativa for incluída na análise bayseana e podem ser muito diferentes para algumas partes do espaço de possíveis dados mesmo se a análise bayseana a prior for relativamente pouco informativa.[20]
Há uma discordância sobre quais dos métodos produz os resultados mais úteis. Raramente a matemática da computação está em questão — intervalos de confiança baseados em distribuições amostrais ou intervalos de credibilidade baseados no teorema de Bayes —, mas a aplicação destes métodos, a utilidade e a interpretação das estatísticas produzidas são debatidos.[80]
Contra-exemplos[editar | editar código-fonte]
Uma vez que a teoria do intervalo de confiança foi proposta, um número de contra-exemplos foi desenvolvido para mostrar como a interpretação dos intervalos de confiança pode ser problemática, pelo menos se forem interpretados de maneira ingênua.[24][25][26]
Procedimento de confiança para localização uniforme[editar | editar código-fonte]
B. L. Welch apresenta um exemplo que claramente mostra a diferença entre a teoria dos intervalos de confiança e outras teorias de estimativas por intervalo (incluindo os intervalos fiduciais de Fisher e os intervalos objetivos de Bayes).[81] G. K. Robinson chama este exemplo de "possivelmente o melhor contra-exemplo conhecido para a versão de Neyman da teoria do intervalo de confiança".[82] Para B. L. Welch, isto mostra a superioridade da teoria do intervalo de confiança. Para críticos, isto mostra a deficiência da teoria do intervalo de confiança. Neste artigo, apresenta-se uma versão simplificada do contra-exemplo.
Supondo que sejam observações independentes da distribuição uniforme , então o procedimento de confiança ótimo de 50% é
.[83]
O argumento fiducial de Fisher ou o objetivo de Bayes podem ser usados para derivar a estimativa do intervalo que também é um procedimento de confiança de 50%.[81]
B. L. Welch mostrou que o primeiro procedimento de confiança domina o segundo procedimento de confiança, de acordo com teoria do intervalo de confiança. Para cada , a probabilidade de o primeiro procedimento conter é menor ou igual a probabilidade de o segundo procedimento conter . A largura média dos intervalos do primeiro procedimento é menor que a largura média dos intervalos do segundo procedimento. Portanto, o primeiro procedimento é preferível sob a teoria clássica do intervalo de confiança. Entretanto, quando , os intervalos do primeiro procedimento com certeza contém o valor real . Consequentemente, o coeficiente de confiança nominal de 50% não está relacionado à incerteza que deve-se ter de que um intervalo específico contenha o valor real. Além disso, quando o primeiro procedimento gera um intervalo muito pequeno, isto indica que estão muito próximo e que, portanto, eles apenas oferecem a informação em um único ponto do dado. Ainda, o primeiro intervalo exclui quase todos os valores razoáveis do parâmetro devido à sua largura pequena. O segundo procedimento não tem esta propriedade.[81]
As duas propriedades contra-intuitivas do primeiro procedimento — 100% de cobertura quando estão afastados e quase 0% de cobertura quando estão próximos — equilibram-se para 50% de cobertura em média. Entretanto, apesar do primeiro procedimento ser ótimo, seus intervalos não oferecem uma avaliação da precisão da estimativa nem uma avaliação da incerteza que deve-se ter do intervalo conter o valor real.
Estes contra-exemplos são usados para argumentar contra interpretações ingênuas dos intervalos de confiança. Se um procedimento de confiança é realizado para ter propriedades além da cobertura nominal (como relacionada à precisão ou à relação com a inferência bayseana), estas propriedades precisam ser provadas (elas não seguem a partir do fato do procedimento ser um procedimento de confiança).[24][25][26]
Procedimento de confiança para [editar | editar código-fonte]
J. H. Steiger sugere um número de procedimentos de confiança de medidas de tamanhos de efeitos comuns em análise de variância.[84] Morey et al. apontam que vários destes procedimentos de confiança, incluindo um para , têm a propriedade de à medida que a estatística torna-se cada vez menor — indicando inadaptação com todos os possíveis valores de — o intervalo de confiança encolhe e pode até conter apenas o valor único . Isto é, o intervalo de confiança é infinitamente apertado. Isto ocorre quando para um intervalo de confiança de .[85]
Este comportamento é consistente com a relação entre o procedimento de confiança e o teste de significância — à medida que torna-se tão pequeno que as médias do grupo estão muito mais próximas que o esperado pela chance, o teste de significância pode indicar rejeição para a maioria ou para todos os valores de . Portanto, o intervalo será muito apertado ou até vazio (ou, pela convenção sugerida por Steiger, conter apenas "0").[84] Entretanto, isto não indica que a estimativa de é muito precisa. Isto indica o oposto, que a confiabilidade dos próprios resultados pode estar em dúvida. Isto é o contrário da interpretação comum dos intervalos de confiança que revelam a precisão da estimativa.[24][25][26]
Questões filosóficas[editar | editar código-fonte]
O princípio por trás dos intervalos de confiança foi formulado para dar uma resposta a uma pergunta levantada em inferência estatística sobre como lidar com a incerteza inerente dos resultados derivados de dados que são eles mesmos um subconjunto selecionado aleatoriamente de uma população. Há outras respostas fornecidas pela inferência bayseana na forma de intervalos de credibilidade.[20]
Os intervalos de confiança correspondem a uma regra escolhida para determinar os limites de confiança, em casos em que esta regra é essencialmente determinada antes de qualquer dado ser obtido ou antes de qualquer experimento ser realizado. Esta regra é definida de tal modo que sobre todos os conjuntos de dados possíveis há uma alta probabilidade (este alta é especialmente quantificada) de o intervalo determinado pela regra incluir o valor real da quantidade em questão. Esta é uma maneira bastante direta e razoável de especificar uma regra para determinar intervalos de incerteza. A abordagem bayseana parece oferecer intervalos que podem, sujeito a aceitação da uma interpretação de probabilidade com probabilidade bayseana, ser interpretados como significando que o intervalo específico calculado a partir de um dado conjunto de dado tem uma probabilidade particular de incluir o valor real, condicional aos dados e as outras informações disponíveis. Isto não é permitido pela abordagem do intervalo de confiança, uma vez que nesta formulação os limites do intervalo e os valores reais são valores fixados e não há aleatoriedade envolvida.[8]
Por exemplo, no caso da pesquisa de intenção de voto na introdução do artigo, para estar 95% confiante que o número real de eleitores que pretendem votar no partido em questão está entre 36% e 44%, não deve ser interpretado de acordo com o senso comum que há probabilidade de 95% que o número real de eleitores que pretendem votar no partido em questão esteja entre 36% e 44%. O real significado de níveis de confiança e intervalos de confiança é muito mais sutil. No caso acima, a interpretação correta seria a seguinte: se a pesquisa for repetida um grande número de vezes (poderia ser produzido um intervalo de confiança de 95% para o intervalo de confiança da pesquisa), cada vez gerando um intervalo de confiança de 95% a partir da amostra da pesquisa, então 95% dos intervalos gerados poderiam conter a porcentagem real de eleitores que pretendem votar no em um determinado partido. Cada vez que a pesquisa é repetida, um intervalo de confiança diferente é produzido. Portanto, não é possível fazer afirmações absolutas sobre probabilidades para qualquer intervalo.[8]
Perguntas referentes a como um intervalo expressando incerteza em uma estimativa pode ser formulado e a como tais intervalos podem ser interpretados não são problemas estritamente matemáticos, mas são problemas filosóficos.[86] A matemática pode assumir o controle uma vez que os princípios básicos de uma abordagem de inferência foram estabelecidos, mas tem apenas um papel limitado em afirmar por que deve-se preferir uma ou outra abordagem. Por exemplo, um nível de confiança de 95% geralmente é usado nas ciências biológicas, mas é uma questão de convenção ou escolha. Nas ciências físicas, um nível muito mais elevado pode ser usado.[87]
Referências
- ↑ a b c d e Neyman, J. (1937). «Outline of a Theory of Statistical Estimation Based on the Classical Theory of Probability». Philosophical Transactions of the Royal Society. 236: 333 – 380
- ↑ «Intervalos de Confiança». Universidade Federal do Paraná (UFPR). Consultado em 21 de março de 2017
- ↑ a b «Intervalo de Confiança». Universidade Federal do Paraná (UFPR). Consultado em 21 de março de 2017
- ↑ «Confidence Intervals». University of Northern Iowa. Consultado em 21 de março de 2017
- ↑ a b «Chapter 9: Confidence Intervals». Georgetown College. Consultado em 21 de março de 2017
- ↑ Kendall, M. G.; Stuart, D. G. (1973). The Advanced Theory of Statistics – Vol 2: Inference and Relationship. Londres: Griffin. pp. seção 20.4
- ↑ a b Cox, D. R.; Hinkley, D. V. (1974). Theoretical Statistics. Londres: Chapman & Hall. pp. 49, 209
- ↑ a b c d Field, Andy (2013). Discovering statistics using SPSS. Londres: SAGE
- ↑ Zar, J. H. (1984). Biostatistical Analysis. New Jersey: Prentice Hall International. pp. 43 – 45
- ↑ Zhou, Mai. «Formulas for Exam 2» (PDF). University of Kentucky. Consultado em 21 de março de 2017
- ↑ a b «Sample Size and Confidence Intervals». Boston University. Consultado em 21 de março de 2017
- ↑ Sullivan, Lisa. «Confidence Intervals». Boston University. Consultado em 21 de março de 2017
- ↑ a b c d Memória, José Maria Pompeu (2004). «Breve História da Estatística» (PDF). Empresa Brasileira de Pesquisa Agropecuária (EMBRAPA)
- ↑ a b «The Legacy of Jerzy Neyman» (PDF)
- ↑ Neyman, Jerzy (1934). «On the Two Different Aspects of the Representative Method: The Method of Stratified Sampling and the Method of Purposive Selection». Journal of the Royal Statistical Society. 97 (4): 558 – 625
- ↑ O'Connor, J. J.; Robertson, E. F. «Biography of Jerzy Neyman». MacTutor History of Mathematics Archive. Consultado em 31 de janeiro de 2017
- ↑ «Estimação para a Proporção Populacional P» (PDF). Universidade de São Paulo (USP). Consultado em 21 de março de 2017
- ↑ a b c d e f «Estimação por Intervalos». Universidade Federal do Paraná (UFPR). Consultado em 21 de março de 2017
- ↑ a b Goldstein, H. (1995). «The Graphical Presentation of a Collection of Means». Journal of the Royal Statistical Society. 158: 175 – 177
- ↑ a b c d e f Charpentier, Arthur (26 de setembro de 2014). «Confidence VS. Credibility Intervals». Freakonometrics. Consultado em 21 de março de 2017
- ↑ Pires, Ana (2000). «Estimação por Intervalos» (PDF). Instituto Superior Técnico (IST). Consultado em 30 de janeiro de 2017
- ↑ Cox, D. R.; Hinkley, D. V. (1974). Theoretical Statistics. Londres: Chapman & Hall. pp. 214, 225, 233
- ↑ Coutinho, Evandro Silva Freire; Cunha, Geraldo Marcelo da (2005). «Conceitos Básicos de Epidemiologia e Estatística para a Leitura de Ensaios Clínicos Controlados» (PDF). Revista Brasileira de Psiquiatria. 27 (2)
- ↑ a b c d e Hoekstra, Rink; Morey, Richard D.; Rouder, Jeffrey N.; Wagenmakers, Eric–Jan (2014). «Robust Misinterpretation of Confidence Intervals» (PDF)
- ↑ a b c d Kalinowski, Pawel (2010). «Identifying Misconceptions about Confidence Intervals» (PDF)
- ↑ a b c d Siegfried, Tom (3 de julho de 2014). «Scientists' Grasp of Confidence Intervals doesn't Inspire Confidence». Science News. Consultado em 30 de janeiro de 2017
- ↑ «Confidence Limits for the Mean». Engineering Statistics Handbook. Consultado em 30 de janeiro de 2017. Arquivado do original em 5 de fevereiro de 2008
- ↑ Mayo, D. G. (1981). «In Defence of the Neyman–Pearson Theory of Confidence Intervals» (PDF). Philosophy of Science. 48 (02): 269 – 280
- ↑ «Estimating Proportions with Confidence» (PDF). University of California – Irvine. Consultado em 22 de março de 2017
- ↑ a b Kalinowski, Pav (2010). «Understanding Confidence Intervals (CIs) and Effect Size Estimation». APS (Association for Psychological Science). Consultado em 30 de janeiro de 2017
- ↑ a b «Confidence Intervals and Nuisance Parameters» (PDF). California Institute of Technology. Consultado em 22 de março de 2017
- ↑ Roussas, George G. (1997). A Course in Mathematical Statistics. [S.l.]: Academic Press. p. 397
- ↑ Feigelson, Eric D.; Babu, G. Jogesh (2012). Modern Statistical Methods for Astronomy – With R Applications. [S.l.]: Cambridge University Press. 45 páginas
- ↑ a b c d «Confidence Interval – Desirable Properties for Data Sets». Consultado em 22 de março de 2017
- ↑ «Estimação da Proporção Populacional p» (PDF). Instituto de Matemática e Estatística da Universidade de São Paulo (IME / USP). Consultado em 3 de abril de 2017
- ↑ «Descriptive Statistics». College of Saint Benedict and Saint John's University. Consultado em 22 de março de 2017
- ↑ Abramovich, Felix; Ritov, Ya'acov (2013). Statistical Theory: A Concise Introduction. [S.l.]: CRC Press. pp. 121 – 122
- ↑ Pereira, Paulo Vitor da Costa (2014). «Uma Revisão da Análise de Variância Multivariada com Aplicações em Biologia» (PDF). Universidade Federal do Rio de Janeiro. p. 31. Consultado em 16 de março de 2017
- ↑ Agranonik, Marilyn (2009). «Equações de estimação generalizadas (GEE): Aplicação em estudo sobre mortalidade neonatal em gemeres de Porto Alegre, RS (1995 - 2007)» (PDF). Universidade Federal do Rio Grande do Sul. Consultado em 16 de março de 2017
- ↑ Smithson, Michael (2003). Confidence Intervals. [S.l.]: Sage Publications. 12 páginas
- ↑ Filho, Augusto Sousa da Silva (24 de fevereiro de 2014). «INFERÊNCIA EM AMOSTRAS PEQUENAS: MÉTODOS BOOTSTRAP». Anhanguera Educacional Ltda. p. 116. Consultado em 15 de março de 2017
- ↑ a b Chiann, Chang. «BOOTSTRAP» (PDF). Instituto de Matemática e Estatística - USP. p. 2. Consultado em 15 de março de 2017
- ↑ Filho, Augusto Sousa da Silva (24 de fevereiro de 2014). «INFERÊNCIA EM AMOSTRAS PEQUENAS: MÉTODOS BOOTSTRAP». Anhanguera Educacional Ltda. p. 3. Consultado em 15 de março de 2017
- ↑ a b c d Bussab, Wilton de O.; Morettin, Pedro A. (2010). Estatística Básica. [S.l.]: Saraiva. p. 311 – 312. 540 páginas
- ↑ a b c d Devore, Jay L. (2005). Probabilidade e Estatística para Engenharia e Ciências. [S.l.]: Cengage Learning. p. 245 – 248. 692 páginas
- ↑ a b c d Ross, Sheldon (2004). Introduction to Probability and Statistics for Engineers and Scientists. [S.l.]: Elsevier. p. 240 – 244. 624 páginas
- ↑ Guerriero, Vincenzo. «Power Law Distribution: Method of Multi–Scale Inferential Statistics». Journal of Modern Mathematics Frontier
- ↑ Rees, D. G. (2001). Essential Statistics. [S.l.]: Chapman and Hall / CRC. pp. seção 9.5
- ↑ Spiegel, Murray R. (2006). Estatística. São Paulo: Pearson. 238 páginas
- ↑ a b c d Spiegel, Murray R. (2006). Estatística. São Paulo: Pearson. pp. 234 – 248
- ↑ Bussab, Pedro A.; Morettin, Pedro A. (2012). Estatística Básica. São Paulo: Saraiva. pp. 310 – 317
- ↑ Spiegel, Murray R. (2006). Estatística. São Paulo: Pearson. 256 páginas
- ↑ a b c Spiegel, Murray R. (2006). Estatística. São Paulo: Pearson. 195 páginas
- ↑ Rodrigues, Alfredo J. «Bioestatística Básica» (PDF). Faculdade de Medicina de Ribeirão Preto da Universidade de São Paulo. Consultado em 3 de abril de 2017
- ↑ Souza, Christopher Freire. Estatística – Uma Abordagem para Hidrólogos. [S.l.: s.n.] p. 26 – 27. 41 páginas
- ↑ Sartoris, Alexandre. «Capítulo 7 - Intervalo de Confiança e Testes de Hipóteses». Estatística e Introdução à Econometria (PDF). [S.l.]: Saraiva. p. 216
- ↑ a b Magalhães, Marcos Nascimento; Lima, Antonio Carlos Pedroso de (2007). Noções de Probabilidade e Estatística. São Paulo: EdUSP. 230 páginas
- ↑ Lohr, Sharon L. (1999). Sampling: Design and Analysis. Pacific Grove, California: Duxbury Press. 49 páginas. ISBN 0-534-35361-4.
The margin of error of an estimate is the half-width of the confidence interval ...
- ↑ Stokes, Lynne; Tom Belin (2004). «What is a Margin of Error?» (PDF). What is a Survey?. Survey Research Methods Section, American Statistical Association. 64 páginas. Consultado em 31 de maio de 2006. Cópia arquivada (PDF) em 12 de março de 2013
- ↑ a b Bussab, Wilton de O.; Morettin, Pedro A. (2012). Estatística Básica. São Paulo: Saraiva. 311 páginas
- ↑ a b Bussab, Wilton de O.; Morettin, Pedro A. (2012). Estatística Básica. São Paulo: Saraiva. 302 páginas
- ↑ Devore, Jay L. (2005). Probabilidade e Estatística para Engenharia e Ciências. [S.l.]: Cengage Learning. pp. 275 – 277. 672 páginas
- ↑ Cox, D. R.; Hinkley, D. V. (1974). Theoretical Statistics. Londres: Chapman & Hall. pp. seção 7.2
- ↑ Knezevic, Andrea (2008). «Overlapping Confidence Intervals and Statistical Significance» (PDF). StatNews – Cornell Statistical Consulting Unit (73)
- ↑ Wolfe, Rory; Hanley, James (8 de janeiro de 2002). «If We're So Different, Why Do We Keep Overlapping?». CMAJ. Consultado em 30 de janeiro de 2016
- ↑ Smith, Daniel (2005). «Overlapping Confidence Intervals are not a Statistical Test». 26th Annual Institute on Research and Statistics
- ↑ Bussab, Wilton de O.; Morettin, Pedro A. (2010). Estatística Básica. [S.l.]: Saraiva. pp. 337 – 339. 540 páginas
- ↑ a b Leshan, Davis. Strategic Communication. [S.l.: s.n.]
- ↑ Ferreira, Clecio. «Cap. 5. Testes de Hipóteses» (PDF). Universidade Federal de Juiz de Fora (UFJF). Consultado em 3 de abril de 2017
- ↑ Rothman, Kenneth J.; Greenland, Sander; Lash, Timothy L. (2008). Epidemiologia Moderna. [S.l.]: Artmed. p. 382 – 383. 886 páginas
- ↑ Rothman, Kenneth J.; Greenland, Sander; Lash, Timothy T. (2008). Epistemiologia Moderna. [S.l.]: Artmed. p. 365 – 366. 886 páginas
- ↑ Härdle, W.; Müller, M.; Sperlich, S.; Werwatz, A. (2004). Nonparametric and Semiparametric Models. [S.l.]: Springer. 65 páginas
- ↑ «Probability and Statistics». Syracuse University. Consultado em 23 de março de 2017
- ↑ Castañeda, Daniel Francisco Neyra. Econometria com Aplicações em R e C. [S.l.: s.n.] 45 páginas
- ↑ D. S. Young (2010), Book Reviews: "Statistical Tolerance Regions: Theory, Applications, and Computation", TECHNOMETRICS, FEBRUARY 2010, VOL. 52, NO. 1, pp.143-144.
- ↑ Krishnamoorthy, K. and Lian, Xiaodong(2011) 'Closed-form approximate tolerance intervals for some general linear models and comparison studies', Journal of Statistical Computation and Simulation,, First published on: 13 June 2011 doi:10.1080/00949655.2010.545061
- ↑ Derek S. Young (5 de agosto de 2010). «tolerance: An R Package for Estimating Tolerance Intervals». Journal of Statistical Software. 36 (5): 1-39. ISSN 1548-7660. Consultado em 19 de fevereiro de 2013
- ↑ Bernardo, José M.; Smith, Adrian F. M. (2000). Bayesian Theory. Nova Iorque: Wiley. 259 páginas
- ↑ «Credible Intervals and Confidence Intervals» (PDF). Consultado em 23 de março de 2017
- ↑ VanderPlas, Jake (junho de 2014). «Frequentism and Bayesianism III: Confidence, Credibility, and why Frequentism and Science do not Mix». Pythonic Perambulations. Consultado em 23 de março de 2017
- ↑ a b c Welch, B. L. (1939). «On Confidence Limits and Sufficiency, with Particular Reference to Parameters of Location». The Annals of Mathematical Statistics. 10 (01): 58 – 69
- ↑ Robinson, G. K. (1975). «Some Counterexamples to the Theory of Confidence Intervals». Biometrika. 62 (01): 155 – 161
- ↑ Pratt, J. W. «Book Review: Testing Statistical Hypotheses by E. L. Lehmann». Journal of the American Statistical Association. 56 (293): 163 – 167
- ↑ a b Steiger, J. H. (2004). «Beyond the F Test: Effect Size Confidence Intervals and Tests of Close Fit in the Analysis of Variance and Contrast Analysis». Psychological Methods. 9 (2): 164 – 182
- ↑ Morey, R. D.; Hoekstra, R.; Rouder, J. N.; Lee, M. D.; Wagenmakers, E. (2016). «The Fallacy of Placing Confidence in Confidence Intervals». Psychonomic Bulletin & Review. 23 (01): 103 – 123
- ↑ Seidenfeld, T. (1979). Philosophical Problems of Statistical Inference: Learning from R.A. Fisher. [S.l.]: Springer–Verlag
- ↑ «Statistical Significance Defined Using the Five Sigma Standard». Data Analysis Blog. Consultado em 30 de janeiro de 2017
Ver também[editar | editar código-fonte]



















































![{\displaystyle \left[{\bar {x}}-z_{\frac {\alpha }{2}}{\frac {\sigma }{\sqrt {n}}},{\bar {x}}+z_{\frac {\alpha }{2}}{\frac {\sigma }{\sqrt {n}}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ba3f9e8c779b2b2fd944b465e3bdf244a80f8510)


![{\displaystyle \left[{\bar {x}}-z_{\frac {\alpha }{2}}{\frac {s}{\sqrt {n}}},{\bar {x}}+z_{\frac {\alpha }{2}}{\frac {s}{\sqrt {n}}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d15d67e94f6a3b98e154d2b246958e4ed6217b2b)
















![{\displaystyle \left[{\bar {x}}-{\frac {cs}{\sqrt {n}}},{\bar {x}}+{\frac {cs}{\sqrt {n}}}\right],\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ad373a73808a03f9d480fb52fbd71ba3f3d8fa74)

![{\displaystyle \left[p_{n}-z_{\frac {\alpha }{2}}{\sqrt {\frac {p_{n}(1-p_{n})}{n}}},\;p_{n}+z_{\frac {\alpha }{2}}{\sqrt {\frac {p_{n}(1-p_{n})}{n}}}\ \right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/64f80410615860eadd7e54b3ce53d92ebe18a2d1)

![{\displaystyle \left.p_{n}+{\sqrt {\frac {n_{p}-n}{n}}}\cdot {\sqrt {\frac {n_{p}-n}{n_{p}-1}}}\ \right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/244c8ed847c7b99fbbc7a564a3badbb6746c9a80)

























































