Média
| Estatística |
|---|
 |
Em estatística, média é definida como o valor que demonstra a concentração dos dados de uma distribuição, como o ponto de equilíbrio das frequências em um histograma.[1] Média também é interpretada como um valor significativo de uma lista de números.[2] Os valores de uma lista de números podem ser representados por meio da escolha aleatória de um número. Se todos os números forem iguais, o número escolhido aleatoriamente será a média. Então, a média pode ser calculada por meio da combinação dos números de maneira específica e da geração de um valor significativo. Entretanto, a palavra média é usualmente usada em métodos mais sofisticados como média aritmética, mediana, moda, entre outros.
Seguindo uma definição mais informal de "média", pode-se assumir que no campo da estatística, dados possuem posições. Por exemplo, cada valor dos lançamentos de um dado possui sua posição em uma planilha eletrônica. Em estatística, média é uma medida de posição que indica um valor uniforme dos dados. Por exemplo, o conjunto possui média aritmética . Embora seja o valor médio, ele não é o valor central definido pela mediana.[3]
História[editar | editar código-fonte]
Origem[editar | editar código-fonte]
O primeiro registro da ampliação da média aritmética de 2 para n casos para realização de estimativas ocorreu no século XVI. Do século XVI em diante, a média gradualmente se tornou um método comum para reduzir erros de medidas em várias áreas.[4][5] Na época, os astrônomos queriam saber o valor real de medições imprecisas com a posição de um planeta ou o diâmetro da lua. Com a média de vários valores medidos, cientistas assumiram que o número de erros era relativamente pequeno em comparação com o total de valores medidos. O método de tirar a média para reduzir os erros de observação foi principalmente desenvolvido na astronomia.[4][6]
Um possível precursor da média aritmética é a mid-range (média de dois valores extremos), usada na astronomia árabe do século IX ao século XI e também na metalurgia e na navegação.[5] Entretanto, há várias outras referências vagas sobre o uso da média aritmética. Elas não são tão claras, mas podem ter relação com a definição moderna de média. De acordo com um texto referente ao século IV:[7]
| “ | Em primeiro lugar, devemos estabelecer uma sequência de números de mônada a 9: 1, 2, 3, 4, 5, 6, 7, 8 e 9. Em seguida, devemos acrescentar o montante de todos os números juntos e, uma vez que a sequência contém nove termos, devemos procurar a nona parte do todo para verificar se ela está naturalmente presente entre os números da sequência, então encontraremos que a propriedade de ser [um] nono [da soma] apenas pertence a própria média [aritmética]. | ” |
Existem potenciais referências ainda mais antigas. Há registros de que por volta de 700 a.C., comerciantes e transportadores concordaram que o dano à carga e ao navio (sua contribuição em casos de danos no mar) deveria ser dividido igualmente entre eles. Isso deve ter sido calculado usando média, embora pareça não haver registros diretos do cálculo.
Etimologia[editar | editar código-fonte]
De acordo com o Oxford English Dictionary, poucas palavras receberam uma maior investigação etimológica.[8]
Em um primeiro uso em inglês da palavra datado do final do século XV, média significava taxas alfandegárias e era usada na região do Mediterrâneo. Em seguida, média passou a significar o custo dos danos ocorridos no mar. Inclusive, surgiu o termo regulador de média para designar a pessoa que decidia como dividir os danos entre os proprietários e os seguradores do navio e da carga.[9] Os danos ocorridos em mar (médias particulares) eram arcados apenas pelos proprietários da carga danificada (média geral), de modo que o proprietário podia reivindicar uma contribuição proporcional de todas as partes do empreendimento marítimo.[9] O tipo de cálculo usado para regular a média geral deu origem ao uso da média como média aritmética.[10]
Em um segundo uso em inglês da palavra datado de 1674, média (averish) significava o resíduo ou o segundo crescimento dos campos de colheita que eram considerados apropriados para consumo pelos animais de tração (avers).[11] A raiz da palavra average (média, em inglês) é encontrada em árabe como awar, em italiano como avaria, em francês como avarie e em holandês como averij. Não está claro em qual língua a palavra apareceu pela primeira vez.[10]
Já em um uso antigo e diferente da palavra datado do século XI, média parecia ser um termo legal para a obrigação de um dia de trabalho para um xerife. O termo legal provavelmente anglicizado de avera foi encontrado no Domesday Book, registro antigo com informações sobre a população inglesa do século XI.[12]
Definição informal[editar | editar código-fonte]

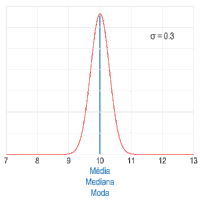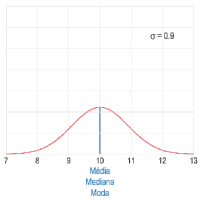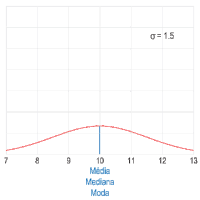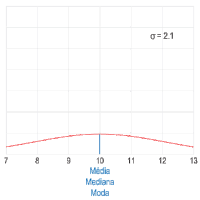
Em estatística, dados possuem posições. Por exemplo, cada valor dos lançamentos de um dado possui sua posição em uma planilha eletrônica. Em estatística, média é uma medida de posição que indica um valor uniforme dos dados. Por exemplo, o conjunto possui média aritmética . Embora seja o valor médio, ele não é o valor central definido pela mediana.[3]
- Dado o rol de uma população, ou seja, todos os indivíduos, a média é representada pela letra grega Mi (.
- No caso de amostras, tem-se por padrão a representação por .
- Essa diferença entre população (todos) ou amostras (parte) também se aplica à variância e ao desvio padrão, conforme representações matemáticas próprias.
Definição formal[editar | editar código-fonte]


Média aritmética[editar | editar código-fonte]
Seja o número total de valores e cada valor, em que . Média aritmética é a soma dos valores dividido pelo número total de valores :
- .[13]
Média geométrica[editar | editar código-fonte]
Média geométrica é a -ésima raiz do produto de todos os valores :
Média geométrica pode ser pensada como o antilogaritmo da média aritmética dos logaritmos dos números. Por exemplo, a média geométrica de 2 e 8 é [14]
Média harmônica[editar | editar código-fonte]
Média harmônica é a recíproca da média aritmética para os valores :
Média harmônica é usada no cálculo de média de velocidade. Por exemplo, se a velocidade de ida um veículo do ponto A ao ponto B é de 60 km/h e a velocidade de volta do mesmo veículo do ponto A ao ponto B é de 40 km/h, então a velocidade média é dada por Entretanto, se o veículo tivesse viajado por metade do tempo em uma velocidade e metade do tempo em outra velocidade, a média aritmética de 50 km/h proveria a noção correta de média.[14]
Média harmônica também é usada no cálculo da resistência equivalente em uma associação de vários resistores em paralelo. Por exemplo, se três resistores de valores R1, R2 e R3 estiverem em paralelo, então a resistência R do circuito é dada por [14]
Observação[editar | editar código-fonte]
Em relação às médias, dado uma população ou amostra com todas as observações positivas e pelo menos dois números distintos, tem-se que:
- Demonstração dado o .
Média Ponderada[editar | editar código-fonte]
Média ponderada é a média aritmética com um coeficiente ponderando os valores. O valor de pode ser sempre igual ou diferente:
Exemplos[editar | editar código-fonte]
Média aritmética[editar | editar código-fonte]
Uma fábrica produz 200, 100, 50, 100, 150 e 200 unidades de um produto entre janeiro e junho. Qual a produção média mensal da fábrica no semestre? Para encontrar a produção média mensal da fábrica no semestre, é preciso calcular a média ou o valor matemático da sua produção média mensal entre janeiro e junho. Se a fábrica tivesse o mesmo desempenho entre janeiro e junho, sua produção total seria unidades no semestre.
Então:
.
Isto é, a fábrica produz em média 133,3 unidades entre janeiro e junho.[16]
Média geométrica[editar | editar código-fonte]
O aumento da taxa de crescimento de uma empresa em novembro e em dezembro foi de e , respectivamente. Qual a taxa de crescimento média mensal da empresa no período?
Embora o cálculo pareça razoável, é preciso encontrar uma mesma taxa de crescimento para o período. O crescimento total da empresa no período foi de . Sejam o crescimento total da empresa em novembro e o crescimento total da empresa em dezembro.
Então:
Isto é, a taxa de crescimento média mensal da empresa foi de cerca de no período.[16]
Média harmônica[editar | editar código-fonte]
Um concurso que distribui anualmente um prêmio de R$ 180 teve 1 ganhador no primeiro ano e 3 ganhadores no segundo ano. Qual foi o prêmio médio dos ganhadores nos dois anos?
O número médio de ganhadores é , o que não significa que o prêmio médio dos ganhadores tenha sido nos dois anos. Para encontrar o prêmio médio dos ganhadores nos dois anos, é preciso calcular o prêmio médios dos ganhadores no primeiro ano e o prêmio médios dos ganhadores no segundo ano. Sejam o prêmio médio do ganhador no primeiro ano e o prêmio médio dos ganhadores no segundo ano.
Então:
Isto é, o prêmio médio dos ganhadores nos dois anos foi .
Em termos algébricos:
Portanto, a média harmônica do total numero de ganhadores em dois anos é .[16]
Média ponderada[editar | editar código-fonte]
Em um grupo de pessoas, 20% delas são adultas e 80% delas são crianças. Os adultos pesam em média 75 quilos e as crianças pesam em média 45 quilos. Qual o peso médio do grupo?
Os adultos correspondem a 20% ou a 0,2 do grupo, enquanto as crianças correspondem a 80% ou a 0,8 do grupo. A média não está correta porque a média dos pesos médios dos adultos e das crianças não demonstram o peso médio do grupo. Se 20% das pessoas do grupo pesam 75 quilos, então 0,2 x 75 = 15 quilos. Se 80% das pessoas do grupo pesam 45 quilos, então 0,8 x 45 = 36 quilos.
Então:
Isto é, o peso médio do grupo é 51 quilos. Foi possível calcular a média ponderada a partir das diferentes proporções entre adultos e crianças no grupo.[17]
Exemplos aplicados ao mercado financeiro[editar | editar código-fonte]
Taxa de retorno e CAGR[editar | editar código-fonte]
A taxa de retorno é um tipo de média usada em finanças. Quando a taxa de retorno é anual, ela é chamada de taxa composta anual de crescimento (CAGR). Seja um investimento em um período de dois anos com taxa de retorno de –10% no primeiro ano e +60% no segundo ano. A taxa de retorno ou a taxa composta anual de crescimento é obtida pelo cálculo da seguinte equação .[18]
O valor de que torna a equação verdadeira é 0,2 (equivalente a 20%), o que significa que o retorno total sobre um investimento em um período de dois anos é igual ao retorno total se houve crescimento de 20% em cada ano. Lembrando que a ordem dos anos não faz diferença (as taxas de retorno de +60% e –10% dariam os mesmos resultados se as taxas de retorno fossem de –10% e +60%).[18]
O método pode ser ampliado para exemplos nos quais os períodos não são iguais. Seja a taxa de retorno de –23% em um período de meio ano e +13% em um período de dois anos e meio. A taxa de retorno para os dois períodos é igual ao retorno anual , obtido pelo cálculo da seguinte equação:, que resulta em uma taxa de retorno de 0,06 ou 6%.[18]
Média móvel[editar | editar código-fonte]
Dada uma série temporal como os preços diários das ações, deseja-se muitas vezes criar uma série mais suave.[19] Isso ajudar demostrar tendências subjacentes ou comportamentos periódicos dos fenômenos. Uma maneira fácil de fazer isso é escolher um número e criar uma série por meio do cálculo da média aritmética dos primeiros valores passo a passo. Sejam preços observados. Então, a sequência de média móvel é definida como . Essa é a forma mais simples de média móvel.
Formas mais complicadas de média móvel envolvem média ponderada. A ponderação pode ser usada para melhorar ou suprimir vários comportamentos periódicos. Há uma análise muito extensa sobre quais ponderações usar na literatura sobre filtro digital. No processamento de sinal, o termo média móvel é usado mesmo quando a soma dos pesos não é 1 (então, a série resultante é uma versão em escala das médias).[20] O motivo é que a análise é geralmente voltada somente para o comportamento periódico. Uma outra generalização é uma média móvel autorregenerativa, em que a média também inclui alguns das médias moveis recém calculadas. Isso permite que amostras antigas históricas afetem resultados de cálculos recentes.[19]
Generalização da média[editar | editar código-fonte]
Entre outros tipos mais sofisticados de média estão tri-média, tri-mediana e média normalizada.[21] É possível criar uma métrica de média usando uma f-média generalizada:
,
em que é qualquer função inversível. Por exemplo, a média geométrica usando e a média harmônica usando . [2]
Entretanto, o método envolvendo médias generalizadas não é geral o suficiente para abordar todas as médias. Um método mais geral para definir uma média envolve qualquer função contínua, estritamente crescente em cada argumento e simétrica (invariante sob a permutação dos argumentos).[22]
A média é o valor que, quando cada argumento é substituído por , resultada no mesmo valor da função: . Essa definição mais geral aborda a propriedade importante de todas as médias, em que a média de uma lista de elementos iguais é o próprio elemento.[2]
A função fornece a média aritmética. A função , em que a lista de elementos é formada por números positivos, fornece a média geométrica. A função , em que a lista de elementos também é formada por números positivos, fornece a média harmônica.[22]
Medidas de tendência central[editar | editar código-fonte]
| Nome | Equação / Descrição |
|---|---|
| Média | Média é o valor médio de uma distribuição. Ela é utilizada para representar todos os valores da distribuição. |
| Média aritmética | [23] |
| Média geométrica | [23] |
| Média harmônica | [24] |
| Média ponderada | [25] |
| Média quadrática (RMS) |
[26] |
| Média cúbica | [3] |
| Média generalizada | [2] |
| Média heroniana | [27] |
| Média aparada (média truncada) | Média aritmética dos valores após um certo número ou uma certa proporção maior e menor terem sido descartados.[28] Entre os casos de média aparada (média truncada), estão a média interquartílica (amplitude interquartícula) que usa a variação interquartílica[29] e a média de Windsor que em vez de excluir os valores extremos os tornam iguais ao maior e ao menor valores restantes. |
Outras medidas de tendência central[editar | editar código-fonte]
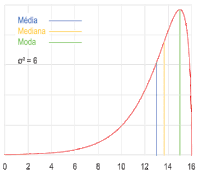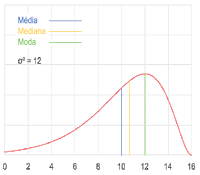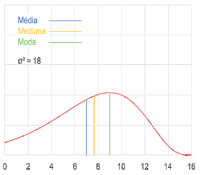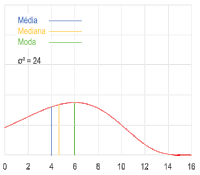
Mediana[editar | editar código-fonte]
O número do meio de uma lista de valores em ordem crescente ou decrescente é chamado de mediana (se houver uma quantidade par de valores, a média dos dois números do meio é calculada). Então, para encontra a mediana é preciso ordenar a lista de valores e excluir os maiores e os menores valores até sobrarem um ou dois números. Se sobrar um número, a mediana será ele. Se sobrarem dois números, a mediana será a média aritmética de ambos. Seja a lista de valores 3, 7, 1 e 13. Se a lista de valores for ordenada para 1, 3, 7 e 13 e 1 e 13 forem removidos, sobrarão 3 e 7. Como sobrarão dois valores, a mediana será a média aritmética .[30][31]
Moda[editar | editar código-fonte]
O número mais frequente em uma lista de valores é chamado de moda. Por exemplo, a moda de uma lista de valores 1, 2, 2, 3, 3, 3, 4 é 3. Em casos em que dois ou mais números aparecem com mesma frequência ou com maior frequência que outros números, não há uma definição acordada de moda. Há autores que afirmam que todos eles são modas e há autores que afirmam que nenhum deles são modas.[30][32]
Referências
- ↑ Paiva, Max. «Matemática e suas Tecnologias» (PDF). FB Vestibular. Consultado em 7 de novembro de 2016
- ↑ a b c d «Estatística: Descritiva». Escola Superior de Agricultura Luiz de Queiroz da Universidade de São Paulo (ESALQ / USP). Consultado em 9 de novembro de 2016
- ↑ a b c Magalhães, Marcos Nascimento; Lima, Antonio Carlos Pedroso de (2015). Noções de Probabilidade e Estatística. São Paulo: EDUSP. 105 páginas
- ↑ a b Placket, R. L. «Studies in the History of Probability and Statistics: VII. The Principle of the Arithmetic Mean». Biometrika: 130 - 135. Consultado em 3 de novembro de 2016
- ↑ a b Eisenhart, Churchill (1971). «The Development of the Concept of the Best Mean of a set of Measurements from Antiquity to the Present Day» (PDF). Consultado em 3 de novembro de 2016
- ↑ Bakker, Arthur. «The Early History of Average Values and Implications for Education». Journal of Statistics Education: 17 - 26. Consultado em 3 de novembro de 2016
- ↑ Waterfield, Robin. «On the Mystical, Mathematical and Cosmological Symbolism of the First Ten Numbers». The Theology of Arithmetic. 70 páginas
- ↑ Oxford English Dictionary. [S.l.]: Oxford University Press. 2005
- ↑ a b «Etymology Again - Average». The Actuary. 2007. Consultado em 7 de novembro de 2016
- ↑ a b «Average». Online Etymology Dictionary. Consultado em 7 de novembro de 2016
- ↑ Ray, John (1780). A Collection of English Words Not Generally Used. London: H. Bruges
- ↑ Kelham, Robert (1788). Domesday Book Illustraded. Londres: John Nichols. 159 páginas
- ↑ Iezzi, Gelson; Hazzan, Samuel; Degenszajn, David Mauro. Fundamentos de Matemática Elementar 11. [S.l.]: Atual. 114 páginas
- ↑ a b c Lima, Elon Lages; Carvalho, Paulo Cezar Pinto; Wagner, Eduardo; Morgado, Augusto César (1998). A Matemática do Ensino Médio. Rio de Janeiro: SBM. 138 páginas
- ↑ Lima, E. L.; Carvalho, P. C. P.; Wagner, Eduardo; Morgado, Augusto César (2004). A Matemática do Ensino Médio. Rio de Janeiro: SBM. 144 páginas
- ↑ a b c Lima, Elon Lages; Carvalho, Paulo Cezar Pinto; Wagner, Eduardo; Morgado, Augusto César (1998). A Matemática do Ensino Médio. Rio de Janeiro: SBM. pp. 139 – 140
- ↑ Lima, Elon lages; Carvalho, Paulo Cezar Pinto; Wagner, Eduardo; Morgado, Augusto César (2004). A Matemática do Ensino Médio. Rio de Janeiro: SBM. 145 páginas
- ↑ a b c Morgado, Augusto Cesar; Wagner, Eduardo; Zani, Sheila C. (1993). Progressões e Matemática Financeira. Rio de Janeiro: SBM. 44 páginas
- ↑ a b Box, George E.P.; Jenkins, Gwilym M. (1976). Time Series Analysis: Forecasting and Control. [S.l.]: Holden-Day
- ↑ Haykin, Simon (1986). Adaptive Filter Theory. [S.l.]: Prentice-Hall
- ↑ Merigo, Jose M.; Cananovas, Montserrat (2009). «The Generalized Hybrid Averaging Operator and its Application in Decision Making». Journal of Quantitative Methods for Economics and Business Administration: 69 - 84
- ↑ a b Bibby, John (1974). «Axiomatisations of the Average and a Further Generalisation of Monotonic Sequences» (PDF). Glasgow Mathematical Journal: 63 – 65
- ↑ a b Lima, Elon Lages; Carvalho, Paulo Cezar Pinto; Wagner, Eduardo; Morgado, Augusto César (2004). A Matemática do Ensino Médio. Rio de Janeiro: SBM. 138 páginas
- ↑ Lima, Elon Lages; Carvalho, Paulo Cezar Pinto; Wagner, Eduardo; Morgado, Augusto César (2004). A Matemática do Ensino Médio. Rio de Janeiro: SBM. 139 páginas
- ↑ Lima, Elon Lages; Carvalho, Paulo Cezar Pinto; Wagner, Eduardo; Morgado, Augusto César (2004). A Matemática do Ensino Médio. Rio de Janeiro: SBM. 144 páginas
- ↑ Lima, Elon Lages; Carvalho, Paulo Cezar Pinto; Wagner, Eduardo; Morgado, Augusto César (2004). A Matemática do Ensino Médio. Rio de Janeiro: SBM. 141 páginas
- ↑ Sýkora, Stanislav (2009). «Mathematical Means and Averages: Generalized Heronian Means». Consultado em 9 de novembro de 2016
- ↑ Silva Filho, Tito Nícias Teixeira da; Figueiredo, Francisco Marcos Rodrigues (2014). «Revisitando as Medidas de Núcleo de Inflação do Banco Central do Brasil» (PDF). Banco Central do Brasil. 4 páginas. Consultado em 10 de novembro de 2016
- ↑ José Fernandes de Melo Filho; Aureo Silva de Oliveira, Leonardo da Costa Lopes e Lucas Melo Vellame (2006). «Análise Estatística Exploratória e Variabilidade da Densidade do Solo em um Perfil de Latossolo Amarelo Coeso do Tabuleiros Costeiros da Bahia». Ciência e Agrotecnologia: 199 - 205. Consultado em 10 de novembro de 2016
- ↑ a b Pinheiro, João Ismael D.; Cunha, Sônia Baptista da; Carvajal, Santiago Ramírez; Gomes, Gastão Coelho (2009). Estatística Básica: A Arte de Trabalhar com Dados. São Paulo: Elsevier. 17 páginas
- ↑ Stevenson, William J. (1986). Estatística Aplicada à Administração. [S.l.]: Habra. pp. 21 – 22
- ↑ Stevenson, William J. (1986). Estatística Aplicada à Administração. [S.l.]: Habra. 23 páginas













![{\displaystyle {\text{MG=}}{\sqrt[{n}]{\prod _{i=1}^{n}x_{i}}}={\sqrt[{n}]{x_{1}x_{2}\cdots x_{n}}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d712b6d8cc8a4893d31f666934abfb3de9c660c4)























![{\displaystyle 1+i={\sqrt[{}]{1,248}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a4b1aeb2001b475b4b684cf2ef55426096207e9f)



















![{\displaystyle y=f^{-1}\left({\frac {1}{n}}\left[f(x_{1})+f(x_{2})+\cdots +f(x_{n})\right]\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5fea48be50f3fe5836ae433848e3e4ca0c9827a5)










![{\displaystyle {\bigg (}\prod _{i=1}^{n}x_{i}{\bigg )}^{1/n}={\sqrt[{n}]{x_{1}\cdot x_{2}\dotsb x_{n}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9b90e69cf6c86c449e462984ec24cb680574276a)



![{\displaystyle {\sqrt[{3}]{{\frac {1}{n}}\sum _{i=1}^{n}x_{i}^{3}}}={\sqrt[{3}]{{\frac {1}{n}}\left(x_{1}^{3}+x_{2}^{3}+\cdots +x_{n}^{3}\right)}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/87ea526bc6b48f6abb52bc522d57c9fedacbaf90)
![{\displaystyle {\sqrt[{p}]{{\frac {1}{n}}\cdot \sum _{i=1}^{n}x_{i}^{p}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b914d893b094e9e15a5681ef60069e9e5fac54ab)

