Variável de confusão
| Estatística |
|---|
 |
Em estatística, uma variável de confusão, também chamada de fator de confusão ou confundidor, é uma variável que influencia tanto a variável dependente, quanto a variável independente, causando uma associação espúria. A variável de confusão é um conceito causal e como tal não pode ser descrita em termos de correlações ou associações.[1][2][3]
Definição[editar | editar código-fonte]
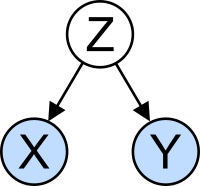
A confusão é definida nos termos do modelo de geração de dados (como na figura ao lado). Considere uma variável independente e uma variável dependente. Para estimar o efeito de sobre , deve-se suprimir os efeitos de variáveis estranhas que influenciam tanto e . Dizemos que e são confundidas por uma outra variável sempre que for a causa tanto de , quanto de .
Considere a probabilidade do evento sob a intervenção hipotética . e não são confundidas se e somente se o seguinte se aplicar:
para todos os valores e , em que é a probabilidade condicional ao ver . Intuitivamente, esta igualdade afirma que e não são confundidas sempre que a associação observada entre elas é igual à observação que seria medida em um experimento controlado, com aleatorizado.
A princípio, a igualdade definidora pode ser verificada a partir do modelo de geração de dados, assumindo que temos todas as equações e probabilidades associadas com o modelo. Isto é feito ao simular uma intervenção e verificar se a probabilidade resultante de é igual à probabilidade condicional .
Controle[editar | editar código-fonte]
Considere que um pesquisador está tentando avaliar a efetividade da droga (drug) , a partir de dados de uma população em que o uso da droga foi uma escolha do paciente. Os dados mostram que o gênero (gender) do paciente () influencia a escolha da droga pelo paciente, assim como suas chances de recuperação (). Neste cenário, gênero () confunde a relação entre e , já que é uma causa tanto de , quanto de :
Temos que:
porque a quantidade observada contém informação sobre a correlação entre e e a quantidade intervencionista não contém (já que não está correlacionada com em um experimento aleatorizado). Certamente, deseja-se a estimativa não viesada , mas nos casos em que apenas os dados observados estão disponíveis, uma estimativa não viesada só pode ser obtida ao "ajustar" para todos as variáveis de confusão, isto é, condicionando sobre seus vários valores e fazendo a média do resultado. No caso de uma única variável de confusão , isto leva à seguinte "fórmula de ajuste":
que dá uma estimativa não viesada para o efeito causal de sobre . A mesma fórmula de ajuste pode funcionar quando há múltiplas variáveis de confusão. A escolha do conjunto de variáveis que garantirá estimativas não viesadas deve ser feita com cautela. O critério para uma escolha adequada é chamado de "porta dos fundos" (backdoor) e exige que o conjunto escolhido "bloqueie" (ou intercepte) todo caminho de a que termina com uma seta em direção a .[4][1] Tais conjuntos são chamados de "admissíveis pela porta dos fundos" e podem incluir variáveis que não são causas comuns de e , mas simples proxies. Retornando ao exemplo do uso da droga, já que atende o requisito da porta dos fundos (isto é, intercepta o caminho pela porta dos fundos ), a fórmula de ajuste de porta dos fundos é válida:
Desta forma, pode-se prever o efeito provável de administrar a droga a partir dos estudos observados nos quais as probabilidades condicionais que aparecem do lado direito da equação podem ser estimadas por regressão.
Ao contrário do que se comumente acredita, adicionar covariáveis ao conjunto de ajuste pode introduzir viés. Um típico contraexemplo ocorre quando é um efeito comum de e , um caso em que não é uma variável de confusão (isto é, o conjunto vazio é admissível pela porta dos fundos) e ajustar para criaria um viés conhecido como viés do colisor ou paradoxo de Berkson.[5]
Geralmente, a confusão pode ser controlada pelo ajuste se e somente se houver um conjunto de covariáveis observadas que satisfaz à condição da porta dos fundos. Além disto, se for tal conjunto, então, a penúltima fórmula de ajuste acima é válida.[6]
História[editar | editar código-fonte]
De acordo com Alfredo Morabia, a palavra "confundir" deriva do verbo do latim medieval "confundere", que significa "misturar", e foi provavelmente escolhida para representar a confusão entre a causa que se deseja avaliar e outras causas podem afetar o resultado e, assim, causar confusão ou ficar no caminho da avaliação desejada.[7] O estatístico britânico Ronald Fisher usou a palavra "confusão" em seu livro de 1935, The Design of Experiments, para denotar qualquer fonte de erro em seu ideal de experimento aleatorizado.[8] De acordo com Jan P. Vandenbroucke,[9] o estatístico húngaro-americano Leslie Kish foi o primeiro a usar a palavra "confusão" no sentido moderno da palavra, para denotar "incomparabilidade" de dois ou mais grupos (por exemplo, exposto e não exposto) em um estudo de observação.[10]
Condições formais que definem o que torna certos grupos "comparáveis" e outros "incomparáveis" foram posteriormente desenvolvidas em epidemiologia por Sander Greenland e James M. Robins,[11] usando a linguagem contrafactual do matemático polaco-americano Jerzy Neyman e do estatístico norte-americano Donald Rubin.[12][13] Estas foram posteriormente suplementadas pelos critérios gráficos, tais como o da condição da porta dos fundos.[3][4]
Demonstrou-se que critérios gráficos são formalmente equivalentes à definição contrafactual, mas mais transparentes aos pesquisadores que dependem de modelos de processos.[1]
Tipos[editar | editar código-fonte]
No caso de avaliações de risco que examinam a magnitude e a natureza do risco à saúde humana, é importante controlar a confusão para isolar o efeito de um perigo particular como um componente alimentício, um pesticida ou uma nova droga. Para estudos prospectivos, é difícil recrutar e avaliar voluntários com o mesmo perfil (idade, dieta, nível de instrução, local de residência, etc.) e, em estudos históricos, pode haver variabilidade semelhante. Devido à inabilidade de controlar a variabilidade de voluntários e estudos com humanos, a confusão é um desafio particular. Por estas razões, experimentos oferecem uma maneira de evitar a maioria das formas de confusão.
Em algumas disciplinas, a confusão é categorizada em diferentes tipos, Em epidemiologia, um tipo é a "confusão por indicação", que diz respeito à confusão em estudos observacionais.[14] Como fatores prognósticos podem influenciar decisões de tratamento (e enviesar estimativas de efeitos de tratamento), controlar os fatores prognósticos conhecidos pode reduzir este problema, mas é sempre possível que um fator esquecido ou desconhecido não seja incluído ou que os fatores interajam entre si de forma complexa. A confusão por indicação tem sido descrita como a limitação mais importantes de estudos observacionais. Ensaios aleatorizados não são afetados pela confusão por indicação devido à atribuição aleatória.
Variáveis de confusão também podem ser categorizadas de acordo com suas fontes, como a escolha do instrumento de medição (confusão operacional), as características situacionais (confusão procedimental) ou as diferenças interindividuais (confusão pessoal):
- Uma confusão operacional pode ocorrer tanto em desenhos de pesquisa experimentais, como em não experimentais. Este tipo de confusão ocorre quando uma medida desenhada para avaliar um construto particular inadvertidamente mede outra coisa também.[15]
- Uma confusão procedimental pode ocorrer em um experimento em laboratório ou em um quase-experimento. Este tipo de confusão ocorre quando o pesquisador erradamente permite que outra variável mude junto com a variável independente manipulada.[15]
- Uma confusão pessoal ocorre quando dois ou mais grupos de unidades são analisados juntos (por exemplo, trabalhadores de diferentes ocupações), apesar de variarem de acordo com uma outra característica (observada ou não observada) ou mais (por exemplo, gênero).[16]
Exemplo[editar | editar código-fonte]
Em outro exemplo, considere que alguém está estudando a relação entre ordem de nascimento (1º filho, 2º filho, etc.) e a presença de Síndrome de Down na criança. Neste cenário, a idade materna seria uma variável de confusão:
- A idade materna mais elevada está diretamente associada com síndrome de Down na criança;
- A idade materna mais elevada está diretamente associada com síndrome de Down, independentemente da ordem de nascimento (se a mãe tiver o primeiro e o terceiro filho depois dos 50 anos, há o mesmo risco);
- A idade materna está diretamente associada com a ordem de nascimento (o segundo filho, exceto no caso de gêmeos, nasce quando a mãe é mais velha do que era quando o primeiro filho nasceu);
- A idade materna não é uma consequência da ordem de nascimento (ter um segundo filho não muda a idade materna).
Em avaliações de risco, fatores como idade, gênero e nível de instrução frequentemente afetam o status de saúde e devem por isso ser controlados. Além destes fatores, pesquisadores podem não considerar ou ter acesso a dados sobre outros fatores causais. Um exemplo diz respeito ao estudo sobre consumo de tabaco na saúde humana. O tabagismo, o consumo de bebidas alcoólicas e a dieta são atividades de estilo de vida relacionadas entre si. Uma avaliação que olha os efeitos do tabagismo, mas não controla o consumo de álcool pode superestimar o risco de fumar.[17] O tabagismo e as variáveis de confusão são revisadas em avaliações de risco ocupacional, tais como de segurança em mineração de carvão.[18] Quando não há uma grande população amostral de não fumantes e abstêmios em uma ocupação particular, a avaliação de risco pode ser enviesada na direção de encontrar um efeito negativo sobre a saúde.
Diminuição do potencial de confusão[editar | editar código-fonte]
Uma redução do potencial para a ocorrência e do efeito das variáveis de confusão pode ser obtida ao aumentar os tipos e os números de comparações realizadas em uma análise. Se as medidas ou as manipulações dos construtos centrais forem confundidas (isto é, se houver confusão operacional ou procedimental), a análise de subgrupo pode não revelar problemas na análise. Adicionalmente, aumentar o número de comparações pode criar outros problemas.
A revisão por pares é um processo que pode ajudar a reduzir instâncias de confusão, seja antes da implementação do estudo ou depois que a análise ocorreu. A revisão por pares se baseia na expertise coletiva no interior de uma disciplina para identificar potenciais fraquezas em desenho e análise de estudos, incluindo formas pelas quais os resultados podem estar baseados em confusão. Da mesma maneira, a replicação pode testar a robustez das descobertas de um estudo sob condições alternativas de estudo ou análises alternativas (por exemplo, controlando potenciais variáveis de confusão não identificadas no estudo inicial).
Pode ser menos provável que efeitos de confusão ocorram e ajam de forma semelhante em momentos e lugares diferentes. Ao selecionar locais de estudo, o ambiente deve ser caracterizado em detalhe para garantir que os locais são ecologicamente semelhantes e, consequentemente, que há menor probabilidade de ter variáveis de confusão. A relação entre variáveis ambientais que possivelmente confundem a análise e os parâmetros medidos pode ser estudada. A informação pertinente às variáveis ambientais pode então ser usada em modelos de locais específicos para identificar variância residual que pode resultar de efeitos reais.[19]
Dependendo do tipo de desenho de estudo em jogo, há várias maneiras de modificar o desenho para ativamente excluir ou controlar variáveis de confusão:[20]
- Estudos de caso-controle atribuem variáveis de confusão a ambos os grupos, casos e controles. Por exemplo, se alguém quiser estudar a causa do infarto do miocárdio e pensar que a idade é uma provável variável de confusão, cada paciente de 67 anos que teve um infarto será pareado com uma pessoa de "controle", saudável e de 67 anos. Em estudos de caso-controle, as variáveis mais frequentemente pareadas são idade e sexo. Estudos de caso-controle são plausíveis apenas quando é fácil encontrar controles, isto é, pessoas cujos atributos, tendo em vista todas as potenciais variáveis de confusão conhecidas, são iguais àqueles dos pacientes do caso. Suponha que um estudo de caso-controle tenta encontrar a causa de uma doença em uma pessoa que 1) tem 45 anos, 2) é afro-americana, 3) mora no Alaska, 4) joga futebol com frequência, 5) é vegetariana e 6) trabalha com educação. Um controle teoricamente perfeito seria uma pessoa que, além de não ter a doença investigada, tem as mesmas características do paciente, além de não ter nenhuma doença que o paciente também não tem — encontrar um controle deste tipo seria uma tarefa dificílima.
- Algum grau de pareamento também é possível e frequentemente realizado ao admitir apenas certos grupos etários ou apenas um sexo na população do estudo, criando um coorte de pessoas que compartilham características semelhantes e assim todos os coortes são comparáveis no que se refere à possível variável de confusão. Por exemplo, se idade e sexo forem pensadas como variáveis de confusão, apenas homens com idade entre 40 e 50 anos estariam envolvidos com um estudo de coorte que avalia o risco de infarto do miocárdio em coortes que são fisicamente ativos ou inativos. Em estudos de coorte, a superexclusão de dados de entrada pode levar pesquisadores a definir muito estreitamente o conjunto de pessoas em situações semelhantes para as quais os pesquisadores consideram o estudo útil, de forma que outras pessoas para as quais a relação causal de fato se aplica podem perder a oportunidade de se beneficiarem das recomendações do estudo. Semelhantemente, a "superestratificação" dos dados de entrada no interior de um estudo pode reduzir o tamanho da amostra em um dado estrato a ponto das generalizações obtidas ao observar os membros daquele estrato apenas não serem estatisticamente significantes.
- Os ensaios duplo-cegos escondem da população do ensaio e dos observadores a que grupo cada um dos participantes pertence. Ao impedir os participantes de saberem se estão recebendo tratamento ou não, o efeito placebo devem ser o mesmo tanto para o grupo de controle, como para o grupo de tratamento. Ao impedir os observadores de saberem a qual grupo cada participante pertence, não deve haver viés por parte dos pesquisadores, seja tratando os grupos diferentemente, seja interpretando os resultados distintamente.
- Estudos randomizados controlados são um método em que a população de estudo é dividida aleatoriamente a fim de reduzir as chances de auto-seleção pelos que participam ou de viés pelos que desenharam o estudo. Antes do experimento começar, os responsáveis pelo teste atribuirão os participantes aos seus grupos (controle, intervenção, paralelo), usando um processo de randomização tal como o uso de um gerador de números aleatórios. Por exemplo, em um estudo sobre os efeitos da atividade física, as conclusões seriam menos válidas se os participantes pudessem escolher se querem participar do grupo de controle que não se exercitará ou do grupo de intervenção que praticará atividade física. O estudo então capturaria outras variáveis além de atividade física, tais como níveis de saúde pré-experimento e motivação para adotar hábitos saudáveis. Do lado do observador, o responsável pelo experimento pode escolher candidatos que mais provavelmente mostrarão os resultados que o estudo quer ver ou pode interpretar resultados subjetivos (uma atitude positiva, mais enérgica) de forma favorável aos seus desejos.
- Como no exemplo acima, pensa-se que a atividade física é um comportamento que protege do infarto do miocárdio e que a idade é uma possível variável de confusão. Na estratificação, os dados amostrados são estratificados por grupo etário — isto significa que a associação entre atividade física e infarto seria analisada para cada grupo etário. Se diferentes grupos etários (ou estratos etários) mostrarem riscos relativos muito diferente, a idade deve ser vista como uma variável de confusão. Há ferramentas estatísticas, como os métodos de Mantel–Haenszel, que respondem pela estratificação de conjuntos de dados.
- Controlar a confusão ao medir as variáveis de confusão conhecidas e inclui-las como covariáveis é uma forma de análise multivariada. Análises multivariadas revelam muito menos informação sobre a força e a polaridade da variável de confusão do que os métodos de estratificação. Por exemplo, se a análise multivariada controla o uso de antidepressivos e não estratifica antidepressivos para tricíclicos e inibidores seletivos de recaptação de serotonina, ignorará que estas duas classes de antidepressivos têm efeitos opostos sobre o infarto do miocárdio e que um efeito é muito mais forte que outro.
Todos estes métodos têm suas desvantagens:
- A melhor defesa disponível contra a possibilidade de resultados espúrios devido à confusão é frequentemente dispensar os esforços com estratificação e, em vez disso, conduzir um estudo aleatorizado de uma amostra suficientemente grande tomada como um todo, de modo que todas as potenciais variáveis de confusão (conhecidas e desconhecidas) serão distribuídas por acaso ao longo dos grupos de estudo e, assim, não correlacionadas com a variável binária para inclusão/exclusão em qualquer grupo.
- Em estudos randomizados controlados e duplo-cegos, os participantes não sabem que estão recebendo tratamento simulado e que podem não receber tratamento efetivo.[21] Há resistência contra estudos randomizados controlados em cirurgia porque pacientes concordariam com uma cirurgia invasiva que traz riscos sob o entendimento de que estão recebendo tratamento.
Ver também[editar | editar código-fonte]
Referências[editar | editar código-fonte]
- ↑ a b c Pearl, Judea (14 de setembro de 2009). Causality (em inglês). [S.l.]: Cambridge University Press. ISBN 9781139643986
- ↑ VanderWeele, Tyler J.; Shpitser, Ilya (2013). «On the definition of a confounder». The Annals of Statistics (em inglês). 41 (1): 196–220. ISSN 0090-5364. doi:10.1214/12-aos1058
- ↑ a b Greenland, Sander; Robins, James M.; Pearl, Judea (1999). «Confounding and Collapsibility in Causal Inference». Statistical Science. 14 (1): 29–46. doi:10.2307/2676645
- ↑ a b Pearl, Judea (24 de outubro de 2011). «Aspects of Graphical Models Connected with Causality». Department of Statistics, UCLA (em inglês)
- ↑ Lee, Paul H. (15 de agosto de 2014). «Should we adjust for a confounder if empirical and theoretical criteria yield contradictory results? A simulation study». Scientific Reports (em inglês). 4 (1). ISSN 2045-2322. doi:10.1038/srep06085
- ↑ Shpitser, Ilya; Pearl, Judea (2008). «Complete Identification Methods for the Causal Hierarchy». J. Mach. Learn. Res. 9: 1941–1979. ISSN 1532-4435
- ↑ Morabia, Alfredo (1 de abril de 2011). «History of the modern epidemiological concept of confounding». Journal of Epidemiology & Community Health (em inglês). 65 (4): 297–300. ISSN 0143-005X. PMID 20696848. doi:10.1136/jech.2010.112565
- ↑ Fisher, Sir Ronald Aylmer (1966). The design of experiments (em inglês). [S.l.]: Hafner Pub. Co.
- ↑ Vandenbroucke, Jan P. (2004). «The history of confounding». Birkhäuser, Basel. A History of Epidemiologic Methods and Concepts (em inglês): 313–325. doi:10.1007/978-3-0348-7603-2_17
- ↑ Kish, Leslie (1959). «Some Statistical Problems in Research Design». American Sociological Review. 24 (3): 328–338. doi:10.2307/2089381
- ↑ Greenland, Sander; Robins, James M. (1 de setembro de 1986). «Identifiability, Exchangeability, and Epidemiological Confounding». International Journal of Epidemiology. 15 (3): 413–419. ISSN 0300-5771. doi:10.1093/ije/15.3.413
- ↑ Neyman, J.; Iwaszkiewicz, K.; Kolodziejczyk, St. (1935). «Statistical Problems in Agricultural Experimentation». Supplement to the Journal of the Royal Statistical Society. 2 (2): 107–180. doi:10.2307/2983637
- ↑ Rubin, Donald B. «Estimating causal effects of treatments in randomized and nonrandomized studies.». Journal of Educational Psychology (em inglês). 66 (5): 688–701. doi:10.1037/h0037350
- ↑ Johnston, S. Claiborne (1 de agosto de 2001). «Identifying Confounding by Indication through Blinded Prospective Review». American Journal of Epidemiology. 154 (3): 276–284. ISSN 0002-9262. doi:10.1093/aje/154.3.276
- ↑ a b 1961-, Pelham, Brett W., (2007). Conducting research in psychology : measuring the weight of smoke 3rd ed. Australia: Thomson Wadsworth. ISBN 0534532942. OCLC 70836619
- ↑ Linda,, Steg,. Applied social psychology : understanding and managing social problems Second ed. Cambridge: [s.n.] ISBN 9781107044081. OCLC 987156961
- ↑ Tjønneland, A.; Grønbaek, M.; Stripp, C.; Overvad, K. (1999). «Wine intake and diet in a random sample of 48763 Danish men and women». The American Journal of Clinical Nutrition. 69 (1): 49–54. ISSN 0002-9165. PMID 9925122
- ↑ Axelson, O. (1 de agosto de 1989). «Confounding from smoking in occupational epidemiology.». Occupational and Environmental Medicine (em inglês). 46 (8): 505–507. ISSN 1351-0711. PMID 2673334. doi:10.1136/oem.46.8.505
- ↑ P., Calow, Peter (2009). Handbook of Environmental Risk Assessment and Management. Oxford: Wiley. ISBN 9781444313192. OCLC 815644970
- ↑ H., Hennekens, Charles; L., Mayrent, Sherry (1987). Epidemiology in medicine 1st ed. Boston: Little, Brown. ISBN 0316356360. OCLC 16890223
- ↑ Emanuel, Ezekiel J.; Miller, Franklin G. (20 de setembro de 2001). «The Ethics of Placebo-Controlled Trials — A Middle Ground». New England Journal of Medicine. 345 (12): 915–919. ISSN 0028-4793. PMID 11565527. doi:10.1056/nejm200109203451211
Leituras adicionais[editar | editar código-fonte]
- Judea, Pearl, (30 de janeiro de 1998). «Why There Is No Statistical Test for Confounding, Why Many Think There Is, and Why They Are Almost Right». Department of Statistics, UCLA (em inglês)
- C., Montgomery, Douglas (2009). Design and analysis of experiments 7th ed. Hoboken, NJ: Wiley. ISBN 9780470128664. OCLC 663975046














