Amplitude interquartil
| Estatística |
|---|
 |

O intervalo interquartil (IIQ) foi desenvolvido no âmbito da estatística a fim de avaliar o grau de espalhamento de dados (dispersão) em torno da medida de centralidade. Para entender o comportamento dos dados (sejam eles discretos ou contínuos) de uma forma mais precisa, busca-se o estudo sobre a dispersão de dados por meio de ferramentas que complementam uma análise geral como o desvio padrão e a variância.[1]
Enquanto o desvio padrão e a variância calculam a medida de dispersão sem levar em conta a ordem dos dados, o intervalo interquartil avalia a dispersão de dados somente depois de ordená-los em ordem crescente. O intervalo interquartil é calculado com base no cálculo de quartis, sendo o primeiro quartil (inferior), o quartil intermediário (mediana), o terceiro quartil (superior), que estão ligados ao conceito de quantil. A diferença entre o quartil superior e o quartil inferior determina o intervalo interquartil.[1]
História[editar | editar código-fonte]

Os termos quartil inferior e quartil superior foram cunhados por Sir Donald MacAlister em 1879 com a publicação de The Law of the Geometric Mean.[2]
Já os termos intervalo interdecil e intervalo interquartil foram cunhados por Francis Galton em 1882 com a publicação de Report of the Anthropometric Committee, embora a ideia de intervalo interquartil tenha aparecido anteriormente nos trabalhos de Carl Friedrich Gauss e Adolphe Quételet. Galton organizou as observações em ordem crescente de magnitude e tomou as frações necessárias de cada extremidade, utilizando a interpolação para obter os pontos de cortes exatos.[3]
Galton reconheceu a maior estabilidade dos quantis mais centrais e usou intervalos interquartis como estatísticas descritivas. Baseando–se nas fórmulas para covariância entre quantis amostrais, Karl Pearson apontou que enquanto a amplitude semi-interquartílica tem a vantagem de estimar diretamente o erro provável, outros pares de quantis amostrais simetricamente espaçados podem fornecer estimadores mais eficientes da variabilidade no caso normal.[4]
Definição formal[editar | editar código-fonte]
O conceito de quartil é importante para a definição de intervalo interquartil. Para esta definição formal é utilizado o conceito de mediana para determinar os quartis ( e ), sendo necessário entender os cálculos tanto para conjuntos de dados com quantidade ímpar de elementos quanto para conjuntos de dados com quantidade par de elementos. É possível determinar a posição dos quartis apenas se os elementos de um conjunto finito de dados estiverem ordenados.[5]
Quartil para conjuntos de dados com quantidade par de elementos[editar | editar código-fonte]
A mediana de um conjunto de dados é a posição que divide igualmente o conjunto em dois grupos, cada um com 50% dos dados. Se possui os elementos com as posições , então é a posição que marca o segundo quartil. Pela definição de mediana, para o caso de um conjunto de dados com quantidade par de elementos, a posição está entre as posições e obtida pelo cálculo . Neste caso, existem elementos de que ocupam as posições e . Estes elementos devem substituir e no cálculo de . Determinando-se , passa a ter uma mediana definida. Então, , em que é uma posição obtida pela média dos elementos e . Isto é, não é um elemento novo de . Os grupos formados a partir do segundo quartil são e .[5]
Observações 1.[editar | editar código-fonte]
- Se e tiverem uma quantidade par de elementos, é realizado o mesmo processo de para determinar o primeiro e o terceiro quartil. Então, a posição do grupo determina o primeiro quartil pelo cálculo . Isto é, . Analogamente, a posição do grupo determina o terceiro quartil pelo cálculo . Então, .[5]
- Pela definição de mediana, se e tiverem uma quantidade ímpar de elementos, o primeiro quartil é calculado por . Neste caso, é utilizado o valor posicional em vez do valor numérico do elemento de para a posição e o terceiro quartil é calculado a partir da quantidade do grupo por . Também neste caso, é utilizado o valor posicional em vez do valor numérico do elemento de para a posição .[5]
O conjunto de dados tem as posições para o primeiro quartil, para o segundo quartil e para o terceiro quartil. Em geral, é utilizada a notação , e para o primeiro quartil, o segundo quartil e o terceiro quartil, respectivamente.[5]
Quartil para conjuntos de dados com quantidade ímpar de elementos[editar | editar código-fonte]
A mediana de um conjunto de dados é a posição que divide igualmente o conjunto em dois grupos, cada um com 50% dos dados. Se possui os elementos com as posições , então é a posição que marca o segundo quartil. Pela definição de mediana, para o caso de um conjunto de dados com quantidade ímpar de elementos, a posição é obtida pelo cálculo . Isto é, . Os grupos formados são e .[5]
Observações 2.[editar | editar código-fonte]
- Se e tiverem uma quantidade par de elementos será realizado o mesmo processo do item 1 do cálculo do quartil para conjuntos de dados com quantidade par de elementos.[5]
- Se e tiverem uma quantidade ímpar de elementos será realizado o mesmo processo do item 2 do cálculo do quartil para conjuntos de dados com quantidade par de elementos.[5]
O conjunto de dados tem as posições para o primeiro quartil, para o segundo quartil e para o terceiro quartil. Lembrando que em geral, é utilizada a notação , e para o primeiro quartil, o segundo quartil e o terceiro quartil, respectivamente.[5]
Intervalo interquartil[editar | editar código-fonte]
Sendo e , o intervalo interquartil é dado por .[6][7]
Observações sobre limite superior e inferior[editar | editar código-fonte]
Na coleta de dados podem ocorrer erros de arredondamentos ou erros de observação. Estes dados são considerados discrepantes dentro de uma mesma amostra e podem levar a erros nas análises sobre a distribuição dos dados. Portanto, estabelece-se o critério de limite inferior e de limite superior nos quartis (os dados que estiverem além destes limites são considerados discrepantes).[8]
Então,
,
em e são o limite inferior e o limite superior, respectivamente.[9]
Embora seja uma constante que pertence aos números reais e pode assumir qualquer valor, é preferível usar o valor . O valor é capaz de captar mais de 99% dos dados embaixo de uma curva normal para mais e para menos do limite superior e do limite inferior, mas não é capaz de captar 100% dos dados deixando uma margem para a visualização dos dados discrepantes.[10]
Então, os cálculos do limite superior e do limite inferior podem ser dados como:
,
em e são o limite inferior e o limite superior, respectivamente.[10]
Discussão[editar | editar código-fonte]
Os outros métodos para encontrar as posições dos quartis podem gerar dúvidas. Por exemplo, ao pensar que e possuem respectivamente 25%, 50% e 75% dos dados de um conjunto , os cálculos dos porcentuais podem ser dados diretamente como:[11][12]
,
em que é número de elementos.[11][12]
Para o conjunto e o primeiro quartil , é visível que a posição não possui 25% dos dados. Logo, este não pode ser o melhor método..[11] Um outro método para definir o quartil é , em que é o número de elementos do conjunto e é a posição do quartil. Então, para definir o terceiro quartil , tem-se Entretanto, a posição não possui 75% dos dados.[12]
Definição informal[editar | editar código-fonte]
Em estatística descritiva, o intervalo interquartil, também denominado por média espalhada, média de 50% ou, mais tecnicamente, propagação de H, é uma medida de dispersão estatística igual à diferença entre os percentis 75 e 25 ou entre o quartil superior e o quartil inferior. Isto é, . Em outras palavras, o intervalo interquartil é a diferença entre o primeiro quartil e o terceiro quartil.[13][14]
O intervalo interquartil é uma medida de variabilidade baseada na divisão de um conjunto de dados em quartis. Os quartis dividem um conjunto de dados em quatro partes iguais. Os valores que separam as partes são chamados de primeiro quartil, segundo quartil e terceiro quartil, indicados por e , respectivamente.[15]
O intervalo interquartil tem um ponto de ruptura de 25%, diferentemente do intervalo total.[16] O intervalo interquartil é usado para construir gráficos de barras, representações gráficas simples de uma distribuição de probabilidade.[17] Para uma distribuição simétrica, em que a mediana é igual ao midhinge (média entre o primeiro quartil e o terceiro quartil), metade do intervalo interquartil é igual ao desvio absoluto médio (DAM). A medida correspondente de tendência central é a mediana.
O intervalo interquartil pode ser usado para identificar outliers (pontos discrepantes em uma distribuição). A partir da metade do intervalo interquartil, tem-se o desvio do quartil ou o intervalo semi-interquartil.[18]
Intervalo semi-interquartil[editar | editar código-fonte]
As medidas de tendência central realizam uma síntese para oferecer uma leitura rápida dos dados. A partir dos conceitos de média, é possível observar no intervalo interquartil uma medida central chamada de desvio quartílico ou intervalo semi-interquartil. O intervalo semi-interquartil é definido como .[19]
O intervalo interquartil, além de avaliar uma dispersão de dados, oferece uma medida de 50% dos dados. Isto favorece uma nova leitura dos dados e comparações com as demais medidas centrais moda, mediana e média.[20]
Diagrama de caixa[editar | editar código-fonte]
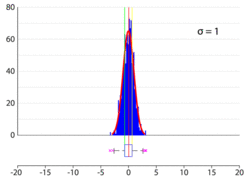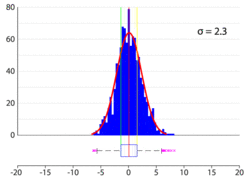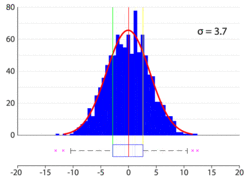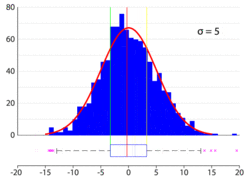
Os dados do intervalo interquartil são úteis para a construção de um diagrama de caixa, também chamado de boxplot. Isto é, os valores de e favorecem a construção da figura abaixo.[17]
Em estatística, usualmente não há uma regra para determinar a largura da caixa (caixa em azul, na figura acima). Com bom senso, adota-se uma largura adequada para o diagrama de caixa. Embora possa ser construído em qualquer direção, o diagrama de caixa geralmente é posicionado na horizontal para facilitar a visualização dos dados. Com o auxílio de uma escala, marca-se a posição de e . Os dados que estão além do limite superior e do limite inferior são representados como pontos ou asteriscos. [21]
Em estatística, os pontos vermelhos na figura acima são chamados de outliers e podem evidenciar algum erro de arredondamento ou erro de observação dos dados. Entretanto, nem sempre os pontos que estão além do limite superior e do limite inferior são outliers. Existem casos em que os outliers são tratados como pontos exteriores ou pontos discrepantes em vez de erros de arredondamento ou erros de observação. Por exemplo, se os 15 municípios brasileiros mais populosos forem colocados em ordem crescente de número de habitantes, São Paulo e Rio de Janeiro serão pontos extremos, o que não configura um erro de arredondamento ou erro de observação.[22]
Exemplos[editar | editar código-fonte]
Exemplo com o uso de mediana[editar | editar código-fonte]
Na sequência numérica , a mediana é o número 10 porque é o número que está exatamente no meio da série. Em uma sequência numérica com quantidade ímpar de elementos, a mediana sempre será o número que está no meio da sequência independente do valor numérico.[23] Em uma sequência numérica com quantidade par de elementos, a mediana será a soma dos dois valores centrais dividido por 2. Por exemplo, para , a mediana será .[24][25]
O intervalo interquartil é a diferença entre a mediana da segunda parte e a mediana da primeira parte do conjunto de dados. Seja a sequência numérica . A mediana da primeira parte é . A mediana da segunda parte é . Portanto, o intervalo interquartil é .
A partir de um conjunto de dados representado em uma tabela, tem-se .[26] Para o cálculo do intervalo semi-interquartil, tem-se .[19]

Exemplo sobre o cuidado com a medida central[editar | editar código-fonte]
Embora ofereçam um resumo dos dados amostrais, o contraexemplo abaixo mostra que as medidas centrais não são suficientes para caracterizar uma avaliação sobre uma sequência numérica.[27]
Sejam os conjuntos de dados:
Todas as sequências possuem média 11, mas visualmente são sequências diferentes entre si. A variabilidade de dados em não existe, mas a variabilidade de dados em é maior do que a variabilidade de dados em . Entretanto, os dados em se mostram mais distantes entre si que os dados em , o que pode induzir ao erro ao admitir que os dados em são mais dispersos que os dados em . Por isso, o cálculo dos quartis e do limite superior e do limite inferior ajudam a evitar erros nas conclusões das análises.[27]
Para evidenciar a sequência numérica com maior variabilidade de dados, pode ser realizada uma comparação entre a distribuição dos dados por meio do intervalo interquartil.[7]
Depois de ordenar os dados, tem-se
Para , e
Para , e
Logo,
Para ,
Para ,
Desta forma, a dispersão de é maior que a dispersão de . Portanto, .[7]
O intervalo interquartil não é suficiente para justificar o fato de possuir os dados mais distantes entre si que . Para identificar a modelagem dos dados de e de , são calculados o limite superior e o limite inferior.[9]
Para ,
Para ,
Desta forma, apenas possui dados discrepantes. Reafirmando, .[9]

A síntese sobre o intervalo é obtida pelo cálculo do intervalo semi-interquartil. [19]
Então,
Para ,
Para ,
As conclusões para uma análise de dados amostrais são:
- não possui dispersão
- se dispersa menos que e vice-versa
- 50% dos dados amostrais estão entre e . Portanto, a medida central de 50% dos dados é:
- Para ,
- Para ,
- O intervalo interquartil demonstra a dispersão dos dados em torno da média de 50% dos dados. Isto é, 50% dos dados amostrais estão no intervalo:
- Para ,
- Para , [20]
Distribuição do intervalo interquartil[editar | editar código-fonte]
O intervalo interquartil de uma distribuição contínua pode ser calculado integrando a função de densidade de probabilidade, que produz a função de distribuição cumulativa (FDC). O quartil inferior é um número tal que a integral da função de distribuição cumulativa de a é igual a 0,25, enquanto que o quartil superior é um número tal que a integral de a é igual a 0,75. Em termos da função de distribuição cumulativa, os quartis podem ser definidos da seguinte forma
,
em que a função de distribuição cumulativa é a função quantil.[28]
O intervalo interquartil e a mediana de algumas distribuições comuns são mostradas na tabela abaixo.
| Distribuição | Mediana | Intervalo interquartil |
|---|---|---|
| Normal | ||
| Laplace | ||
| Cauchy |
Teste do intervalo interquartil para normalizar a distribuição[editar | editar código-fonte]
As medidas intervalo interquartil, média e desvio padrão de uma população podem ser usadas em um teste simples, em que pode ou não pode ser uma distribuição normal. Se for normalmente distribuída, então o score do primeiro quartil é e o score do terceiro quartil é . Dado a média e o desvio padrão para , se for normalmente distribuída:[29][30]
Se os valores reais do primeiro quartil ou do terceiro quartil diferirem substancialmente dos valores calculados, não é normalmente distribuída. Entretanto, uma distribuição normal pode ser perturbada para manter e , scores e e não ser normalmente distribuída, de modo que o teste acima produza um resultado falso positivo. Há outros testes de normalidade mais indicados, como o gráfico .[31]
Outras medidas de dispersão[editar | editar código-fonte]
Desvio padrão[editar | editar código-fonte]
Em probabilidade, o desvio padrão ou desvio padrão populacional (comumente representado pela letra grega ) é uma medida de dispersão em torno da média populacional de uma variável aleatória. Já em estatística, o desvio padrão ou desvio padrão amostral (comumente representado pela letra latina ) é uma medida de dispersão dos dados em torno de média amostral. Um baixo desvio padrão indica que os pontos dos dados tendem a estar próximos da média ou do valor esperado.[32] Um alto desvio padrão indica que os pontos dos dados estão espalhados por uma ampla gama de valores. O desvio padrão populacional ou amostral é a raiz quadrada da variância populacional ou amostral correspondente, de modo a ser uma medida de dispersão que seja um número não negativo e que use a mesma unidade de medida dos dados fornecidos.[33][34][35]
Variância[editar | editar código-fonte]
Em probabilidade e estatística, a variância de uma variável aleatória ou de um processo estocástico é uma medida de dispersão estatística que inda o quão longe os valores encontram-se do valor esperado.[36]
Outras amplitudes[editar | editar código-fonte]
Amplitude do intervalo de classe[editar | editar código-fonte]
A amplitude do intervalo de classe é definida pela diferença entre o limite superior e o limite inferior da própria classe. Isto permite verificar se em uma dada distribuição de frequências as classes possuem a mesma amplitude, evitando erros nos cálculos de quartis e desvios de interpretação.[37]

Amplitude do intervalo de confiança[editar | editar código-fonte]
A amplitude do intervalo de confiança é definida pela diferença entre o limite superior e o limite inferior do próprio intervalo.
Em termos matemáticos,
,
em que é a confiança, é o desvio padrão e é o tamanho da amostra.[38]
Em estatística, também é comum o uso de semi-amplitude como erro de estimação.
Em termos matemáticos,
,
em que é a confiança, é o desvio padrão e é o tamanho da amostra.[38]
Referências
- ↑ a b Pinheiro, João Ismael D.; Carvajal, Santiago R. Ramírez; Cunha, Sonia Baptista da; Gomes, Gastão Coelho (2012). Probabilidade e Estatística. São Paulo: CAMPUS. p. 90. 568 páginas
- ↑ «Statistics How To». Consultado em 16 de fevereiro de 2017
- ↑ Striteska, H. (2006). «The History of Robust Estimation at the Turn of the 19th and 20th Century» (PDF). Proceedings of Contributed Papers: 27 – 30
- ↑ David, H. A. (1998). «Early Sample Measures of Variability». Statistical Science. 13 (4): 368 – 377
- ↑ a b c d e f g h i Morettin, Pedro A.; Bussab, Wilton de O. (2014). Estatística Básica. São Paulo: Saraiva. pp. 43 – 45
- ↑ Silva, Ermes Medeiros da; Silva, Elio Medeiros da; Gonçalves, Valter; Murolo, Afrânio Carlos (1999). Estatística. São Paulo: Atlas. p. 89
- ↑ a b c Lauretto, Marcelo de Souza. «Estatística descritiva básica: Medidas de dispersão» (PDF). Escola de Artes, Ciência e Humanidades - USP. p. 6. Consultado em 7 de fevereiro de 2017. Arquivado do original (PDF) em 22 de fevereiro de 2017
- ↑ Farias, Ana Maria Lima de; Laurencel, Luiz da Costa (2006). «ESTATÍSTICA DESCRITIVA» (PDF). UNIVERSIDADE FEDERAL FLUMINENSE. p. 56. Consultado em 25 de abril de 2017. Arquivado do original (PDF) em 17 de maio de 2017
- ↑ a b c Lauretto, Marcelo de Souza. «Estatística descritiva básica: Medidas de dispersão» (PDF). Escola de Artes, Ciência e Humanidades - USP. p. 9. Consultado em 7 de fevereiro de 2017. Arquivado do original (PDF) em 22 de fevereiro de 2017
- ↑ a b Bussab, Wilton de O.; Morettin, Wilton de O. (2012). Estatística Básica. São Paulo: Saraiva. p. 50. 548 páginas
- ↑ a b c Pinheiro, João Ismael D.; Carvajal, Santiago S. Ramírez; Cunha, Sonia Baptista da; Gomes, Gastão Coelho (2012). Probabilidade e Estatística. São Paulo: CAMPUS. p. 247. 568 páginas
- ↑ a b c «Construção dos quartis» (PDF). Instituto de Assistência Médica ao Servidor Público Estadual de São Paulo (IAMSPE). Consultado em 22 de março de 2017
- ↑ Upton, Graham; Cook, Ian (1996). Statistics. United Kingdom: Oxford University Press. p. 55. ISBN 0-19-914391-9
- ↑ ZWILLINGER, DANIEL; KOKOSKA, STEPHEN (2000). CRC Standard Probability and Statistics Tables and Formulae. Washington, D.C: CHAPMAN & HALL/CRC. p. 18. ISBN 1-58488-059-7
- ↑ Bussab, Wilton de O.; Morettin, Pedro A. (2004). Estatística Básica. São Paulo: Saraiva. p. 42. 548 páginas. ISBN 85-02-03497-9
- ↑ Rousseeuw, Peter J. (1992). «Explicit Scale Estimators with High Breakdown Point» (PDF). North-Holland. pp. 77 – 92. Consultado em 17 de janeiro de 2017. Arquivado do original (PDF) em 22 de outubro de 2016
- ↑ a b Bussab, Wilton de O.; Morettin, Pedro A. (2012). Estatística Básica. São Paulo: Saraiva. p. 48. 548 páginas
- ↑ Yule, G. Udny (1911). An Introduction to the Theory of Statistics. [S.l.]: Charles Griffin and Company. pp. 147 – 148
- ↑ a b c Spiegel, Murray R. (2006). Estatística. São Paulo: Pearson. p. 115. 643 páginas
- ↑ a b Spiegel, Murray R. (2006). Estatística. São Paulo: Pearson. p. 116. 643 páginas
- ↑ Farias, Ana Maria Lima de. «O BOXPLOT» (PDF). UNIVERSIDADE FEDERAL FLUMINENSE. p. 1. Consultado em 8 de fevereiro de 2017. Arquivado do original (PDF) em 6 de julho de 2016
- ↑ Bussab, Wilton de O.; Morettin, Pedro A. (2012). Estatística Básica. São Paulo: Saraiva. p. 49. 548 páginas
- ↑ Morettin, Pedro A.; Bussab, Wilton de O. Bussab (2004). Estatística Básica. São Paulo: Saraiva. p. 45. 548 páginas. ISBN 85-02-03497-9
- ↑ Simon, Laura J. «Descriptive Statistics». Statistical Education Resource Kit. Pennsylvania State Department of Statistics
- ↑ Weisstein, Eric W. «Statistical Median». MathWorld – A Wolfram Web Resource. Consultado em 14 de novembro de 2016
- ↑ Magalhães, Marcos Nascimento; Lima, Antonio Carlos Pedroso (2007). Noções de Probabilidade e Estatística. São Paulo: EdUSP. p. 31. 428 páginas
- ↑ a b SIlva, Ermes Medeiros da (1999). Estatística. São Paulo: Atlas. p. 100
- ↑ Oliveira, Hélio Magalhães de. «Introdução à Estatística» (PDF). Universidade Federal do Pernambuco. p. 49. Consultado em 25 de abril de 2017
- ↑ «Standard Scores». University of Texas-Houston. p. 1. Consultado em 26 de abril de 2017
- ↑ Abebe, A.; Daniels, J.; McKean, J. W.; Kapenga, J. A. (1 de janeiro de 2001). «Normal Quantiles». Western Michigan University. p. 1. Consultado em 26 de abril de 2017
- ↑ Pérez, Fernando Lucambio. «Gráficos para verificar normalidade» (PDF). Universidade Federal do Paraná. Consultado em 26 de abril de 2017
- ↑ Bland, J. Martin; Altman, Douglas G. «Measurement Error» (PDF). BMJ. Consultado em 23 de janeiro de 2017
- ↑ Saporta, Gilbert (2006). Probabilités – Analyse des Données et Statistiques. Paris: Éditions Technip. p. 25. 622 páginas
- ↑ Saporta, Gilbert (2006). Probabilités – Analyse des Données et Statistiques,. Paris: Éditions Technip. p. 119. 622 páginas
- ↑ Saporta, Gilbert (2006). Probabilités – Analyse des Données et Statistiques. Paris: Éditions Technip. p. 121. 622 páginas
- ↑ RUNGER, George C.; MONTGOMERY, Douglas C. Applied Statistics and Probability for Engineers. 3rd ed. Mídia em CD: 2002.
- ↑ Spiegel, Murray R. (2006). Estatística. São Paulo: Pearson. p. 41. 643 páginas
- ↑ a b Magalhães, Marcos Nascimento (2007). Noções de Probabilidade e Estatística. São Paulo: EdUSP. p. 230. 428 páginas
Ligações externas[editar | editar código-fonte]



























































































































