Função contínua
Foram assinalados vários problemas nesta página ou se(c)ção: |
História[editar | editar código-fonte]
"... será chamado de função contínua, se ... os valores numéricos da diferença diminuem arbitrariamente, conforme varie ... "[1]
Cauchy (1821) introduziu o conceito de função contínua, onde pequenas variações em x produzem pequenas variações em . Weierstrass (1874) reformulou a definição de Cauchy, onde a diferença será arbitrariamente pequena, se a diferença for suficientemente pequena.
Posteriormente, com um tratamento mais rigoroso da matemática e a consequente evolução do pensamento matemático, as funções contínuas foram abstraídas para outros campos além da análise: álgebra linear, álgebra abstrata, física matemática, etc.
| Cálculo |
|---|
|
Cálculo especializado |
Definições de continuidade[editar | editar código-fonte]
Em matemática, uma função é contínua quando, intuitivamente, as pequenas variações nos objetos correspondem a pequenas variações nas imagens. Nos pontos onde a função não é contínua, diz-se que a função é descontínua, ou que se trata de um ponto de descontinuidade.
Espaço topológico[editar | editar código-fonte]
Diz-se que uma função entre espaços topológicos é contínua se a imagem recíproca de qualquer aberto de é um aberto de .
Exemplos[editar | editar código-fonte]

Estes exemplos usam propriedades da imagem recíproca, ou seja, dada uma função e um conjunto o conjunto
- Seja um conjunto com a topologia discreta com qualquer topologia, então qualquer função é contínua.
Basta ver que, aberto temos que, e portanto é aberto, o que mostra que é uma função contínua.
- Seja um conjunto com a topologia grosseira com qualquer topologia, então qualquer função é contínua.
De fato, pois, como os dois únicos abertos de são e basta verificar se suas imagens inversas são abertos. Mas e e, por definição, e são abertos em qualquer topologia em
- Sejam e funções contínuas. Então também é uma função contínua.
Fato pois: qualquer que seja aberto, pela continuidade de temos que é um aberto em Portanto, pela continuidade de é um aberto em Mas o que prova a continuidade de em espaço métrico.
Diz-se que uma função é contínua no ponto se é um ponto isolado do domínio ou, caso seja ponto de acumulação de se existir o limite de com tendendo a e esse limite for igual a
OBS.: Não faz sentido calcular limites em pontos que não são de acumulação. Caso insistíssemos teríamos que qualquer valor seria limite de com tendendo a
Em análise real, essa definição é escrita na forma tradicional Epsilon-Delta, ou seja, diz-se que uma função é contínua num ponto do seu domínio se, dado tal que então
Esta definição, com uma pequena adaptação, pode ser usada para uma função de um espaço métrico em outro espaço métrico a função é contínua em quando dado tal que
Em termos de bolas, dados dois espaços métricos dizemos que a aplicação é contínua em se, dada uma bola aberta de centro e raio pode-se encontrar uma bola de centro e raio tal que [2]
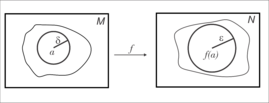
Diz-se que f é contínua em seu domínio, ou simplesmente contínua, se ela for contínua em todos os pontos desse domínio.
Exemplo[editar | editar código-fonte]
- Seja e espaços métricos não vazios. Se tivermos que então a aplicação é contínua e a constante é chamada de constante de Lipschitz. Na reta Real toda aplicação Lipschitiziana é uniformemente contínua.
Equivalência das definições[editar | editar código-fonte]
Se e são espaços métricos, e as topologias geradas pelas métricas em e então uma função é contínua pela definição topológica se, e somente se, ela é contínua pela definição métrica.
Em termos de limites[editar | editar código-fonte]
Uma função é dita ser contínua em um ponto de seu domínio se:
Função sequencialmente contínua[editar | editar código-fonte]
Uma função em que e são espaços topológicos, é sequencialmente contínua em um ponto quanto ela comuta com o limite de sequências, ou seja, quando para toda sequência cujo limite (em ) seja temos que o limite (em ) de é Uma forma elegante de escrever isso é
Propriedades[editar | editar código-fonte]
- Função Composta: Se e são funções contínuas, então é imediato (pela definição topológica) que a função composta é contínua.
- Se é uma bijeção contínua de um espaço topológico compacto em um espaço topológico de Hausdorff então é um homeomorfismo.
- O conjunto dos zeros de uma aplicação contínua entre um espaço topológico e a reta real com a topologia usual, é um conjunto fechado. Em particular, o conjunto das matrizes singulares é fechado em pois o determinante define uma aplicação contínua nesse espaço.
- Sejam e dois espaços topológicos, e uma aplicação contínua. Então restrita a ainda é uma aplicação contínua.
Funções contínuas e suas relações[editar | editar código-fonte]
Álgebra linear[3][editar | editar código-fonte]
Considere um conjunto e o conjunto definido por todas as funções reais . Temos que, assume a estrutura de espaço vetorial a partir das operações de soma e produto por escalar usuais de funções reais, a saber, onde e . Seja e defina então o conjunto das funções contínuas reais. Ora, visto que , a soma de funções contínuas é função contínua e que o produto por escalar é função contínua, temos que é subespaço vetorial de .
Teorema da esfera cabeluda[4][editar | editar código-fonte]
O conceito de continuidade permite ser também para campos vetoriais,[5] tendo então campos vetoriais contínuos. Com isso, temos uma aplicação belíssima do conceito de continuidade em um teorema chamado de Esfera Cabeluda. Eis sua interpretação, informalmente:
"... muitos dos leitores confrontam-se todas as manhãs com o teorema da bola cabeluda, ao tentarem pentear o seu cabelo e verificando que há um redemoinho persistente no topo das suas cabeças. De um modo simplificado, o teorema afirma que não é possível “pentear-se” uma superfície esférica coberta de “cabelo” sem se formarem “redemoinhos” de algum tipo." [6]
Isto pelo fato da superfície esférica admite um campo vetorial contínuo. Também, o teorema da esfera cabeluda é uma consequência de um teorema de Poincaré sobre superfícies contínuas.
Gravação digital[7][editar | editar código-fonte]
As funções contínuas são muito úteis em gravações digitais, como por exemplo, em mídias de CD e DVD. Suponhamos que você esteja querendo gravar com seu celular uma aula de uma determinada disciplina. Como isso funciona? O(A) professor(a) emite uma onda sonora que é uma função contínua, porém como funções contínuas exigiriam uma capacidade de memória muito grande do seu celular (pois são infinitas), o que ele faz na verdade é gravar pedaços da onda sonora a cada segundo (isto é, com uma alta frequência), discretizando a função contínua. Com isso, seu celular tem informações suficientes para reproduzir o som como se fosse seu(sua) professor(a).
Administração e economia[8][editar | editar código-fonte]
A maioria das funções que modelam os fenômenos econômicos são de natureza discreta e possuem descontinuidades finitas, do tipo função escada. As funções preço e custo são discretas, devido à natureza da mercadoria, ou possuem descontinuidade pois o custo e preço decrescem (crescem) instantaneamente. As funções oferta e demanda também são comumente discretas e apresentam descontinuidades.
Referências
- ↑ CAUCHY (1821). Cours d’Analyse. [S.l.: s.n.]
- ↑ LAGES, Elon (1977). Espaços métricos. Rio de Janeiro: IMPA. 32 páginas
- ↑ LIMA,, Elon Lages (2016). Álgebra Linear. Rio de Janeiro: IMPA. pp. 3,4
- ↑ «Teorema da esfera cabeluda»
- ↑ «Campos vetoriais»
- ↑ NUNES, João Pimentel. «"O Teorema da Bola Cabeluda"» (PDF). Dep. Matem´atica, IST, Lisboa
- ↑ «How Analog and Digital Recording Works»
- ↑ WEBER, Jean E. (2001). Matemática para economia e administração. São Paulo: HARBRA. pp. 149–153
Bibliografia[editar | editar código-fonte]
- Munkres, J. (1966). Elementary Differential Topology, edição revisada. Col: Annals of Mathematics Studies 54. [S.l.]: Princeton University Press. ISBN 0-691-09093-9
- Lima, Elon Lages (2013). Análise Real - Funções de uma variável. Col: Coleção Matemática Universitária. 1 12ª ed. [S.l.]: IMPA. 198 páginas. ISBN 978-85-244-0048-3





















































































