Espaço vetorial
Este artigo ou secção resulta, no todo ou em parte, de uma tradução do artigo «Vector space» na Wikipédia em inglês, na versão original. |

Um espaço vetorial (também chamado de espaço linear) é uma coleção de objetos chamada vetores, que podem ser somados um a outro e multiplicados ("escalonados") por números, denominados escalares. Os números reais são escalares frequentemente utilizados, mas também existem espaços vetoriais com multiplicação por números complexos, números racionais; em geral, por qualquer corpo.[1] As operações de adição de vetores e multiplicação por escalar precisam satisfazer certas propriedades, denominadas axiomas (listados abaixo, em § Definição). Para explicitar se os escalares são números reais ou complexo, os termos espaço vetorial real e espaço vetorial complexo são frequentemente utilizados.
Vetores euclidianos são um exemplo de espaço vetorial. Eles representam quantidades físicas como forças: quaisquer duas forças (do mesmo tipo) podem ser somadas para resultar em uma terceira, enquanto que a multiplicação de um vetor de força por um número real gera outro vetor de força. De forma semelhante, porém com um sentido mais geométrico, vetores que representam deslocamentos em um plano ou em um espaço tridimensional também formam espaços vetoriais. Vetores em espaços vetoriais não necessitam ser objetos do tipo seta, como aparecem nos exemplos mencionados acima; vetores são tratados como entidades matemáticas abstratas com propriedades particulares, que, em alguns casos, podem ser visualizados por setas.
Espaços vetoriais são o objeto de estudo da álgebra linear e são bem caracterizados pela sua dimensão, que, grosso modo, especifica o número de direções independentes no espaço. Espaços vetoriais de dimensão infinita surgem naturalmente em análise matemática, como em espaços funcionais, cujos vetores são funções. Esses espaços vetoriais são munidos em geral de uma estrutura adicional, que pode ser uma topologia, permitindo a consideração de conceitos como proximidade e continuidade. Dentre essas topologias, aquelas que são definidas por uma norma ou um produto interno são mais frequentemente utilizadas, por possuírem uma noção de distância entre dois vetores. Esse é o caso particularmente com os espaços de Banach e os espaços de Hilbert, que são fundamentais em análise matemática.
Historicamente, as primeiras ideias que levaram ao conceito de espaços vetoriais podem ser associadas aos avanços, durante o século XVII, nas áreas de geometria analítica, matrizes, sistemas de equações lineares, e vetores euclidianos. O tratamento moderno e mais abstrato, formulado pela primeira vez por Giuseppe Peano em 1888, contém objetos mais gerais que o espaço euclidiano, mas muito da teoria pode ser visto como uma extensão de ideias da geometria clássica como retas, planos, e seus análogos de dimensão mais alta. Atualmente, os espaços vetoriais permeiam a matemática, a ciência e a engenharia. Eles são a noção apropriada da álgebra linear para lidar com sistemas de equações lineares. Eles oferecem um escopo para as séries de Fourier, que são utilizadas em métodos de compressão de imagens, e eles fornecem um ambiente que pode ser utilizado para técnicas de solução de equações diferenciais parciais. Ademais, espaços vetoriais fornecem uma maneira abstrata, livre de coordenadas, de lidar com objetos geométricos e físicos como tensores. Isso por sua vez permite a análise de propriedades locais variedades por técnicas de linearização. Espaços vetoriais podem ser generalizados de diversas maneiras, acarretando noções mais avançadas em geometria e em álgebra abstrata.
Não é necessário que os vetores tenham interpretação geométrica, mas podem ser quaisquer objetos que satisfaçam os axiomas abaixo. Polinômios de grau menor ou igual a () formam um espaço vetorial,[2] por exemplo, assim como grupos de matrizes [3] e o espaço de todas as funções de um conjunto no conjunto R dos números reais.
| Estruturas algébricas |
|---|
Introdução e definição[editar | editar código-fonte]
O conceito de espaço vetorial será primeiramente explicado pela descrição de dois exemplos específicos:
Primeiro exemplo: setas em um plano[editar | editar código-fonte]
O primeiro exemplo de um espaço vetorial consiste de setas em um plano fixo, começando por um ponto fixo. Isso é usado em física para descrever forças ou velocidades. Dadas duas setas deste tipo, v e w, o paralelogramo formado por elas contém uma seta diagonal que também começa na origem. Essa nova seta é chamada de soma das setas anteriores e é denotada por v + w. No caso especial de duas setas na mesma linha, a soma delas é a seta na mesma linha cujo comprimento é a soma ou a diferença dos comprimentos, dependendo se as setas possuem mesmo sentido ou sentidos opostos. Uma outra operação que pode ser feita com setas é o seu escalonamento: dado qualquer número real positivo a, a seta que tem a mesma direção que v, mas está dilatada ou contraída ao multiplicar seu comprimento por a, é chamada multiplicação de v por a. É denotada por av. Quando a for negativo, av é definido como a seta apontando no sentido oposto.
A seguir estão alguns exemplos: se a = 2, o vetor resultante aw tem a mesma direção que w, mas está esticado, tendo um comprimento que é o dobro de w (imagem abaixo, à direita). De forma equivalente, 2w é a soma de w + w. Além disso, (−1)v = −v tem o sentido oposto e o mesmo comprimento que v (vetor azul apontando para baixo, na imagem à direita).

|
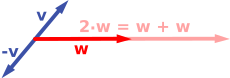
|
Segundo exemplo: pares ordenados de números[editar | editar código-fonte]
Um segundo exemplo chave de um espaço vetorial é fornecido por pares de números reais x e y. (A ordem das componentes x e y é importante, de modo que um par também seja chamado de par ordenado.) Tal par é escrito como (x, y). A soma de dois desses pares e a multiplicação de um par por um número são definidas da seguinte maneira:
- (x1, y1) + (x2, y2) = (x1 + x2, y1 + y2)
e
- a (x, y) = (ax, ay).
O primeiro exemplo acima reduz-se a esse se as setas forem representadas por um par de coordenadas cartesianas do seus pontos finais.
Definição[editar | editar código-fonte]
Neste artigo, os vetores são representados em negrito para distingui-los de escalares.[nota 1]
Um espaço vetorial sobre um corpo K é um conjunto V munido de duas operações que satisfazem os oito axiomas abaixo.
- A primeira operação, chamada de adição de vetores ou simplesmente adição + : V × V → V, leva quaisquer dois vetores v e w e associa a eles um terceiro vetor, normalmente escrito como v + w, e chamado de soma dos dois vetores iniciais. (O vetor resultante também é um elemento de V.)
- A segunda operação, chamada de multiplicação por escalar · : K × V → V, toma qualquer escalar a e qualquer vetor v e fornece um outro vetor av. (Similarmente, um vetor av é um elemento do conjunto V.)
Elementos de V são normalmente denominados vetores. Elementos de K são comumente denominados escalares.
Nos dois exemplos acima, o corpo utilizado é o corpo dos números reais e o conjunto de vetores consiste das setas planas com um ponto fixo de início e de pares de números reais, respectivamente.
Para qualificar um conjunto como sendo um espaço vetorial, ele V e suas operações de adição e multiplicação devem obedecer às condições impostas a seguir, denominadas axiomas.[4] Na lista abaixo, sejam u, v e w vetores arbitrários de V, e a e b escalares em K.
| Axioma | Significado |
|---|---|
| Associatividade da adição | u + (v + w) = (u + v) + w. |
| Comutatividade da adição | u + v = v + u. |
| Elemento identidade da adição | Existe um elemento 0 ∈ V, denominado vetor nulo, tal que v + 0 = v para todo v ∈ V. |
| Elemento inverso da adição | Para todo v ∈ V, existe um elemento −v ∈ V, chamado de inverso aditivo de v, tal que v + (−v) = 0. |
| Compatibilidade da multiplicação por escalar com a multiplicação do corpo | a(bv) = (ab)v. [nota 2] |
| Elemento identidade da multiplicação por escalar | 1v = v, em que 1 denota a identidade multiplicativa em K. |
| Distributividade da multiplicação por escalar em relação à adição de vetores | a(u + v) = au + av. |
| Distributividade da multiplicação por escalar em relação a adição do corpo | (a + b)v = av + bv. |
Esses axiomas generalizam as propriedades dos vetores introduzidos nos exemplos acima. De fato, o resultado da adição de dois pares ordenados (como no segundo exemplo acima) não depende da ordem dos somandos:
- (xv, yv) + (xw, yw) = (xw, yw) + (xv, yv).
Da mesma forma, no exemplo geométrico de vetores como setas, v + w = w + v como o paralelogramo que define a soma dos vetores é independente da ordem dos vetores. Todos os outros axiomas podem ser verificados de forma semelhante nos outros exemplos. Portanto, ao ignorar a natureza concreta desse tipo particular de vetores, a definição incorpora esses dois exemplos e muitos outros em uma noção unificadora de espaço vetorial.
A subtração de dois vetores e a divisão por escalar (não nulo) pode ser definido como
- .
Quando o corpo dos escalares K é o dos números reais R, o espaço vetorial é chamado de espaço vetorial real; quando for o dos números complexos C, o espaço vetorial é chamado de espaço vetorial complexo. Esses dois casos são aqueles mais frequentemente utilizados em engenharia. A definição geral de espaço vetorial permite que os escalares sejam elementos de qualquer corpo fixo K. A noção é então abstraída para um espaço vetorial sobre K. Um corpo é, essencialmente, um conjunto de números que possui as operações de adição, subtração, multiplicação e divisão.[nota 3] Por exemplo, os números racionais formam um corpo.
Em contraste com a intuição provinda de vetores em um plano ou em outros objetos de dimensão maior, existe, em espaços vetoriais gerais, a noção de vizinhanças, ângulos e distâncias. Para lidar com essas questões, tipos particulares de espaços vetoriais são introduzidos.
Formulações alternativas e consequências elementares[editar | editar código-fonte]
A adição de vetores e a multiplicação por escalar são operações que satisfazem a propriedade de fechamento: u + v e av pertencem a V para todo a em K, e u, v em V. Algumas referências mais antigas mencionam essas propriedades como axiomas separados.[5]
No linguajar da álgebra abstrata, os primeiros quatro axiomas são equivalentes a requerer que o conjunto de vetores seja um grupo abeliano sob adição. Os axiomas restantes dão a esse a estrutura de módulo sobre K. Em outras palavras, existe um homomorfismo de anéis f do corpo K para o anel de endomorfismo do grupo de vetores. A multiplicação por escalar av é então definida como (f(a))(v).[6]
Há várias outras consequências diretas dos axiomas de espaço vetorial. Algumas delas são derivadas teoria dos grupos elementar, aplicada ao grupo aditivo de vetores: por exemplo, o vetor nulo 0 de V e o inverso aditivo −v de um vetor v são únicos. Outras propriedades seguem ao empregar também a lei de distributividade da multiplicação por escalar; por exemplo, av é igual a 0 se e somente se a é igual a 0 ou v é igual a 0.
História[editar | editar código-fonte]
Espaços vetoriais têm sua origem no ramo da geometria afim, surgindo a partir da introdução de coordenadas no plano ou no espaço tridimensional. Por volta de 1636, os matemáticos franceses René Descartes e Pierre de Fermat forneceram as bases da geometria analítica ao identificar soluções de uma equação a duas variáveis com pontos em uma curva plana.[7] Para obter soluções geométricas sem utilizar-se de coordenadas, Bolzano introduziu, em 1804, certas operações com pontos, linhas e planos; hoje, esses objetos podem ser vistos como antecessores de vetores.[8] Esse trabalho foi utilizado por Möbius em 1827 para introduzir o conceito de coordenadas baricêntricas.[9] A fundação para a definição de vetores foi a noção de Bellavitis de um "duplo ponto" ("bipoint"), um segmento orientado em que uma das extremidades é a origem e a outra é um alvo. Vetores foram repensados com a apresentação de números complexos por Argand e Hamilton, e pela criação dos quaterniões pelo último.[10] Eles são elementos em R2 e R4; o tratamento deles utilizando combinações lineares remete a Laguerre em 1867, que também definiu sistema de equações lineares.
Em 1857, Cayley introduziu a notação matricial que permitiu a harmonização e a simplificação de mapas lineares. Na mesma época, Grassmann estudou o cálculo baricêntrico iniciado por Möbius. Ele vislumbrou conjuntos de objetos abstratos munidos de certas operações.[11] Em seu trabalho, os conceitos de independência linear e dimensão, bem como o de produtos escalares, estavam presentes. De fato, a obra de Grassmann de 1844 excede o escopo dos espaços vetoriais atuais, já que ele também considera multiplicação entre vetores, o que caracteriza o conceito moderno de álgebra. O matemático italiano Peano foi o primeiro a fornecer uma definição moderna de espaços vetoriais e de transformações lineares em 1888.[12]
Um desenvolvimento importante dos espaços vetoriais foi a construção de espaços funcionais por Henri Lebesgue. Isso foi posteriormente formalizado por Banach e Hilbert, por volta de 1920.[13] À época, a álgebra e o novo ramo da análise funcional começaram a interagir, notavelmente com conceitos-chave como os espaços de funções p-integráveis e os espaços de Hilbert.[14] Também nessa época, iniciaram-se os primeiros estudos de espaços vetoriais de dimensão infinita.
Exemplos[editar | editar código-fonte]
Espaço do vetor nulo[editar | editar código-fonte]
Seja formado por um único elemento Então, definindo-se e para todo elemento de um corpo temos que é um espaço vetorial com como corpo de escalares. Obviamente, como é o elemento neutro de isto é, este espaço vetorial é representado por
Espaços de coordenada[editar | editar código-fonte]
O exemplo mais simples de um espaço vetorial sobre um corpo K é o próprio corpo, equipado com suas adição e multiplicação padrão. De forma mais geral, todas n-uplas (sequências de comprimento n)
- (a1, a2, ..., an)
de elementos do corpo K formam um espaço vetorial que é usualmente denotado por Kn e chamado de espaço de coordenadas.[15] O caso n = 1 é o caso mais simples mencionado acima, no qual o corpo K também é percebido como um espaço vetorial sobre si mesmo. O caso K = R e n = 2 foi discutido na introdução acima.
Números complexos e outras extensões de corpos[editar | editar código-fonte]
O conjunto de números complexos C (isto é, números que podem ser escritos na forma x + iy, para números reais x e y, em que i é a unidade imaginária) formam um espaço vetorial sobre os reais com a adição e a multiplicação definidas usualmente: (x + iy) + (a + ib) = (x + a) + i(y + b) e c ⋅ (x + iy) = (c ⋅ x) + i(c ⋅ y) para números reais x, y, a, b e c. Os vários axiomas de um espaço vetorial seguem do fato de que as mesmas regras se mantêm para a aritmética dos números complexos.
De fato, o exemplo dos números complexos é essencialmente o mesmo (isto é, é isomórfico) ao espaço vetorial de pares ordenados de números reais mencionado acima: se pensarmos no número complexo x + i y como uma representação do par ordenado (x, y) no plano complexo, então percebe-se que as regras de soma e multiplicação de escalares correspondem exatamente ao exemplo anterior.
De modo mais geral, extensões de corpo fornecem uma outra classe de exemplos de espaços vetoriais, particularmente em álgebras e em teoria algébrica dos números: um corpo K que contém um corpo menor E é um espaço vetorial em E, pelas mesmas operações de adição e multiplicação definidas para K.[16] Por exemplo, os números complexos são um espaço vetorial sobre R, e a extensão de corpo é um espaço vetorial sobre Q.
Espaços funcionais[editar | editar código-fonte]

Funções de qualquer conjunto fixo Ω para um corpo K também formam espaços vetoriais, ao realizar adição e multiplicação por escalar ponto a ponto. Ou seja, a soma de duas funções f e g é a função (f + g) dada por
- (f + g)(w) = f(w) + g(w),
e de modo semelhante para a multiplicação. Espaços funcionais desse tipo surgem em várias situações geométricas, quando Ω é a reta real ou um intervalo, ou outros subconjuntos de R. Muitas noções em topologia e análise, como continuidade, integrabilidade ou diferenciabilidade são bem comportadas em relação à linearidade: somas e múltiplos escalares de funções com essas propriedades ainda as preservam.[17] Portanto, o conjunto dessas funções é um espaço vetorial. Elas são estudadas em maior detalhe usando métodos de análise funcional. Restrições algébricas também geram espaços vetoriais: o espaço vetorial K[x] é dado por funções polinomiais:
- f(x) = r0 + r1x + ... + rn−1xn−1 + rnxn, em que os coeficientes r0, ..., rn estão em K.[18]
Equações lineares[editar | editar código-fonte]
Sistemas de equações lineares homogêneas estão proximamente relacionados com os espaços vetoriais vector spaces.[19] Por exemplo, as soluções de
a + 3b + c = 0 4a + 2b + 2c = 0
são dadas por triplas com a arbitrário, de modo que b = a/2 e c = −5a/2. Elas formam um espaço vetorial: somas e múltiplos escalares de tais triplas precisam também satisfazer às mesmas razões entre as três variáveis; logo, elas também são soluções. Matrizes podem ser usadas para condensar várias equações lineares como acima em uma equação vetorial, a saber
- Ax = 0,
em que A = é a matriz que contém os coeficientes das equações que compõem o sistema, x é o vetor (a, b, c), Ax denota um produto matricial, e 0 = (0, 0) é o vetor nulo. De forma semelhante, as soluções de equações diferenciais lineares homogêneas formam espaços vetoriais. Por exemplo,
- f′′(x) + 2f′(x) + f(x) = 0
implica que f(x) = a e−x + bx e−x, em que a e b são constantes arbitrárias, e ex é a função exponencial.
Base e dimensão[editar | editar código-fonte]

Bases permitem representar vetores como uma sequência de escalares denominados coordenadas ou componentes. Uma base é um conjunto (finito ou infinito) B = {bi}i ∈ I de vetores bi, que por conveniência são frequentemente indexados por um conjunto de índices I, que gera todo o espaço é linearmente independente. "Gerar todo o espaço" significa que qualquer vetor v pode ser expresso por uma soma finita (chamada de combinação linear) dos elementos da base:
-
(1)
em que ak são escalares, chamados de coordenadas (ou de componentes) do vetor v em relação à base B, e bik (k = 1, ..., n) são os elementos de B. Independência linear significa que as coordenadas ak são univocamente determinadas para qualquer vetor no espaço vetorial.
Por exemplo, os vetores de coordenadas e1 = (1, 0, ..., 0), e2 = (0, 1, 0, ..., 0), até en = (0, 0, ..., 0, 1), formam uma base de Kn, chamada de base canônica, já que qualquer vetor (x1, x2, ..., xn) pode ser expresso de forma única como uma combinação linear desses vetores:
- (x1, x2, ..., xn) = x1(1, 0, ..., 0) + x2(0, 1, 0, ..., 0) + ... + xn(0, ..., 0, 1) = x1e1 + x2e2 + ... + xnen.
As coordenadas correspondentes x1, x2, ..., xn são exatamente as coordenadas cartesianas de um vetor.
Todo espaço vetorial possui uma base. Isso é uma consequência do lema de Zorn, uma formulação equivalente do axioma da escolha.[20] Dados os outros axiomas da teoria de conjuntos de Zermelo–Fraenkel, a existência de bases é equivalente ao axioma da escolha.[21] O teorema do ultrafiltro, que é mais fraco do que o axioma da escolha, implica que todas as bases de um determinado espaço vetorial têm o mesmo número de elementos, ou cardinalidade (ver Teorema da dimensão para espaços vetoriais).[22] Ela é chamada de dimensão do espaço vetorial, e é denotada por dim V. Se o espaço for gerado por um número finito de vetores, os enunciados acima podem ser provados sem um enfoque tão fundamental quanto o da teoria de conjuntos.[23]
A dimensão do espaço de coordenadas Kn é n, pelo que foi exibido acima. A dimensão do anel de polinômios K[x] introduzida acima é enumeravelmente infinita, sendo que uma base é 1, x, x2, ... A fortiori, a dimensão de espaços funcionais mais gerais, tal como o espaço de funções em um intervalo (limitado ou ilimitado), é infinita.[nota 4] Sob suposições adequadas de reguralidade dos coeficientes envolvidos, a dimensão do espaço de solução de uma equação diferencial ordinária homogênea é igual ao grau da equação.[24] Por exemplo, os espaço de soluções da equação acima é gerado por e−x e {{xe−x}}. Essas duas funções são linearmente independentes sobre os reais R, de modo que a dimensão do espaço gerado seja 2, assim como o grau da equação.
Uma extensão de corpo sobre os racionais Q pode ser pensada como um espaço vetorial sobre Q (ao definir a soma de vetores como a soma de elementos do corpo, e definir a multiplicação por escalar como a multiplicação por elementos de Q, e por outro lado ignorando a multiplicação do corpo). A dimensão (ou grau) da extensão de corpo Q(α) sobre Q depende de α. Se α satisfaz algumas equação polinomial
Aplicações lineares e matrizes[editar | editar código-fonte]
A relação entre dois espaços vetoriais pode ser expressa como um mapeamento linear ou uma transformação linear. Elas são funções que refletem a estrutura do espaço vetorial — isto é, elas preservam soma e multiplicação por escalar:
- e f(a · v) a · f(v) para todo v e w em V, e todo a em K.[27]
Um isomorfismo é uma transformação linear f : V → W tal que exista uma função inversa g : W → V, a qual é um mapeamento tal que as duas possíveis composições f ∘ g : W → W e g ∘ f : V → V sejam a função identidade. De forma equivalente, f é um-pra-um (injetora) e é sobre o contradomínio (sobrejetora).[28] Se existir um isomorfismo entre V e W, os dois espaços são ditos isomórficos; eles então são essencialmente o mesmo espaço vetorial, já que todas as identidades válidas em V são, através de f, levadas a identidades semelhantes em W, e vice-versa através de g.
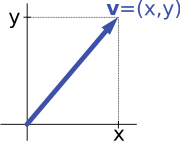
Por exemplo, as "setas em um plano" e os "pares ordenados de números", que são cada qual um espaço vetorial, são isomórficos: uma seta v em um plano que sai da origem de algum sistema (fixo) de coordenadas pode ser expresso por um par ordenado de números ao considerar as componentes x e y da seta, como mostrado na imagem ao lado. Por outro lado, dado um par (x, y), a seta que está à direita pela quantidade x (ou à esquerda, se x for negativo), e está para cima pela quantidade y (ou para baixo, se y for negativo) retorna a seta v.
As transformações lineares V → W entre dois espaços vetoriais formam um espaço vetorial HomK(V, W), também denotado por L(V, W).[29] O espaço das transformações lineares de V para o corpo K é chamado de espaço dual, e é denotado por V∗.[30] Através do mapa natural injetivo V → V∗∗, qualquer espaço vetorial pode ser embutido no seu bidual; o mapeamento é um isoformismo se e somente se o espaço tem dimensão finita.[31]
Uma vez que uma base de V é escolhida, as transformações lineares f : V → W ficam completamente determinadas ao se especificar a imagem dos vetores da base, já que qualquer elemento de V é escrito de forma única como combinação linear desses vetores.[32] Se dim V = dim W, uma correspondência 1-para-1 entre as bases fixadas de V e W acarreta uma aplicação linear que mapeia qualquer elemento da base de V ao elemento correspondente da base de W; isto é, por definição, um isomorfismo.[33] Logo, dois espaços vetoriais são isomórficos se as suas dimensões são as mesmas. Outra forma de expressar isso é que qualquer espaço vetorial é completamente classificado (a menos de um isomorfismo) pela sua dimensão, um único número. Em particular, qualquer espaço vetorial n-dimensional V de tipo K é isomórfico a Kn. Não existe, no entanto, nenhum isomorfismo "canônico" ou preferencial; de fato, um isomorfismo φ : Kn → V é equivalente à escolha da base de V, ao mapear os vetores da base canônica de Kn para V, através de φ. A liberdade em escolher uma base conveniente é particularmente útil no contexto de dimensão infinita.
Matrizes[editar | editar código-fonte]

Matrizes são uma noção útil para representar transformações lineares.[34] Elas são escritas como uma tabela retangular de escalares (imagem ao lado). Qualquer matriz A m-por-n gera um mapeamento linear de Kn para Km da seguinte maneira:
- , em que denota um somatório,
ou, usando multiplicação de matrizes de A com o vetor de coordenadas x:
- x ↦ Ax.
Ademais, após escolher bases de V e de W, qualquer transformação linear f : V → W é representada de forma única por uma matriz através desse procedimento.[35]
O determinante det (A) de uma matriz quadrada A é um escalar que diz se o mapeamento associado à matriz é um isomorfismo ou não: para isso, é suficiente e necessário que o determinante seja não nulo.[36] A transformação linear de Rn que corresponde a uma matriz n-by-n real preserva a orientação se e somente se seu determinante for positivo.
Autovetores e autovalores[editar | editar código-fonte]
Endomorfismos, aplicações lineares do tipo f : V → V, são particularmente importantes já que nesse caso vetores v podem ser comparados com a sua imagem sob f, f(v). Qualquer vetor não nulo v que satisfaz a condição λv = f(v), em que λ é um escalar, é denominado autovetor de f com autovalor λ.[37] De maneira equivalente, v é um elemento do núcleo da diferença f − λ · Id (em que Id é a função identidade V → V). Se V tem dimensão finita, essa afirmação pode ser reformulada usando determinantes: f ter um autovalor λ é equivalente a
- det(f − λ · Id) = 0.
Ao desenvolvê-la através da definição de determinante, a expressão à esquerda pode ser analisada enquanto função polinomial de variável λ, chamada de polinômio característico de f.[38] Se o corpo K for abrangente o suficiente para conter uma raiz desse polinômio (o que acontece automaticamente quando K for algebricamente fechado, tal como K = C), qualquer aplicação linear tem pelo menos um autovetor. O espaço vetorial V pode ou não possuir uma base de autovetores. Esse fenômeno é regido pela forma canônica de Jordan da aplicação.[39][nota 5] O conjunto de todos os autovetores associados a um certo autovalor de f forma um espaço vetorial conhecido como autoespaço. Para alcançar o teorema espectral, a afirmação correspondente do caso em que a dimensão é infinita, as ferramentas da análise funcional são necessárias.
Construções básicas[editar | editar código-fonte]
Além dos exemplos concretos citados anteriormente, existem várias construções de álgebra linear padrão que acarretam espaços vetoriais a outros previamente fornecidos. Eles também são caracterizados pelas propriedades universais, que determinam um objeto X ao especificar as transformações lineares dele para qualquer outro espaço vetorial.
Subespaços e espaços quociente[editar | editar código-fonte]

Um subconjunto não-vazio W de um espaço vetorial V que é fechado sob adição e multiplicação por escalar (e portanto contém o vetor nulo 0 de V) é chamado de subespaço vetorial de V, ou simplesmente um subespaço de V, quando o objeto em questão for, de forma não ambígua, um espaço vetorial.[40][nota 6] Subespaços de V são espaços vetoriais próprios (sobre o mesmo corpo). A interseção de todos os subespaços contendo um determinado conjunto S de vetores é denominado como seu espaço vetorial gerado (ou, ainda, ger ou span), e é o menor subespaço de V contendo o conjunto S. Expressado em termos de elementos, o span é o subespaço que contém todas as combinações lineares dos elementos de S.[41]
Um subespaço vetorial de dimensão 1 é uma linha vetorial. Um subespaço de dimensão 2 é um plano vetorial. Um subespaço vetorial que contém todos a menos de um dos elementos de uma base do espaço prinicpal é um hiperplano vetorial. Em um espaço vetorial de dimensão finita n, um hiperplano de vetores é portanto um subespaço de dimensão n – 1.
A contrapartida dos subespaços são os espaços vetoriais quocientes.[42] Dado qualquer subespaço W ⊂ V, o espaço quociente V/W ("V módulo W") é definido da seguinte maneira: enquanto conjunto, ele consiste de v + W = {v + w : w ∈ W}, em que v é um vetor arbitrário em V; enquanto espaço vetorial, a soma de dois elementos desse tipo v1 + W e v2 + W é dada por (v1 + v2) + W, e a multiplicação por escalar obedece a relação a · (v + W) = (a · v) + W. A questão chave dessa definição é que v1 + W = v2 + W se e somente se a diferença de v1 e v2 estiver em W.[nota 7] Dessa maneira, o espaço quociente "esquece" da informação contida no subespaço W.
O núcleo ker(f) (do inglês, kernel) de uma transformação linear f : V → W consiste em vetores v que são mapeados para o vetor 0 em W (o vetor nulo de W).[43] Tanto o núcleo quanto a imagem im(f) = {f(v) : v ∈ V} são subespaços de V e W, respectivamente.[44] A existência de núcleos e imagens é parte do enunciado de que a categoria de espaços vetoriais (sobre um corpo fixo K) é uma categoria abeliana, isto é, um corpo de objetos matemáticos e de transformações que preservem a estrutura entre eles (uma categoria), que se comporta de forma muito semelhante a uma categoria de grupos abelianos.[45] Por causa disso, enunciados como o teorema do núcleo e da imagem (também chamado de teorema do posto e da nulidade, no contexto de matrizes),
- V / ker(f) ≡ im(f),
podem ser formulados e provados de uma maneira similar ao que se faria para demonstrar enunciados equivalentes para grupos.
Um exemplo importante é o do núcleo da transformação linear x ↦ Ax para alguma matriz fixa A. O núcleo dessa aplicação é o subespaço dos vetores x tais que Ax = 0, que é exatamente o conjunto das soluções do sistema de equações lineares homogêneas associadas a A. Esse conceito também se estende para equações diferenciais lineares, cuja forma geral é
- , em que os coeficientes ai são também funções de x.
Na transformação linear correspondente
- ,
as derivadas da função f aparecem de forma linear (ao contrário de f′′(x)2, por exemplo). Como a diferenciação é um procedimento linear (isto é, (f + g)′ = f′ + g ′ e (c·f)′ = c·f′ para uma constante c), essa transformação também é linear, denominada um operador diferencial linear. Em particular, as soluções da equação diferencial D(f) = 0 formam um espaço vetorial (sobre R ou sobre C).
Produto direto e soma direta[editar | editar código-fonte]
O produto direto de espaços vetoriais e a soma direta de espaços vetoriais são duas maneiras de combinar uma família indexada de espaços vetoriais em um novo espaço vetorial.
O produto direto de uma família de espaços vetoriais Vi consiste em um conjunto de todas as ênuplas (vi)i ∈ I, que especificam para cada índice i em algum conjunto de índices I um elemento vi de Vi.[46] Adição e multiplicação por escalar são realizadas componente a componente. Uma variação dessa construção é a soma direta (também chamada coproduto e denotada por ), em que somente as ênuplas com um número finito de vetores nulos são permitidas. Se o conjunto de índices I é finito, as duas construções são a mesma; porém, de forma mais geral, elas são distintas.
Produto tensorial[editar | editar código-fonte]
O produto tensorial V ⊗F W, ou simplesmente V ⊗ W, de dois espaços vetoriais V e W é uma das noções centrais da álgebra multilinear, que lida com noções estendidas como a de transformações lineares a várias variáveis. Um mapeamento g : V × W → X é chamado de bilinear se g é linear em ambas as variáveis v e w. Isto é, para um w fixo o mapa v ↦ g(v, w) é linear no sentido acima; isso então também é válido para um v fixo.
O produto tensorial é um espaço vetorial particular que é um receptor universal de mapeamentos bilineares g, como a seguir. Ele é definido como um espaço vetorial que consiste de somas (formais) finitas de símbolos chamados de tensores
- v1 ⊗ w1 + v2 ⊗ w2 + ... + vn ⊗ wn,
sujeitos às regras
- a · (v ⊗ w) = (a · v) ⊗ w = v ⊗ (a · w), em que a é um escalar,
- (v1 + v2) ⊗ w = v1 ⊗ w + v2 ⊗ w, e
- v ⊗ (w1 + w2) = v ⊗ w1 + v ⊗ w2.[47]

Essas regras garantem que o mapa f de V × W para V ⊗ W, que envia a ênupla (v, w) para v ⊗ w, seja bilinear. A universalidade enuncia que dado qualquer espaço vetorial X e qualquer mapa bilinear g : V × W → X, existe um mapa único u, mostrado no diagrama com uma seta pontilhada, cuja composição com f é igual a g: u(v ⊗ w) = g(v, w).[48] Isso é chamado de propriedade universal do produto tensorial, uma ocorrência do método — muito utilizado em álgebra abstrata avançada — de indiretamente definir objetos ao especificar mapas de ou para esse objeto.
Espaços vetoriais com estrutura adicional[editar | editar código-fonte]
Do ponto de vista da álgebra linear, os espaços vetoriais são completamente compreendidos na medida em que qualquer espaço vetorial é caracterizado, de modo isomórfico, pela sua dimensão. Contudo, espaços vetoriais por si só não oferecem um escopo no qual é possível responder à questão — essencial para análise — de quando, ou se, uma série de funções converge para outra função. Da mesma forma, a álgebra linear não é adaptada para lidar com séries infinitas, já que a operação de adição permite somente a soma de um número finito de termos. Assim, as demandas do ramo da análise funcional fazem com que sejam considerados espaços vetoriais com estrutura adicional.
Um espaço vetorial pode ser parcialmente ordenado ≤, de modo que certos vetores possam ser comparados.[49] Por exemplo, um espaço vetorial real n-dimensional Rn pode ser ordenado ao se comparar os vetores componente à componente. Espaços vetoriais ordenados, como os espaços de Riesz, são fundamentais para a formulação da integral de Lebesgue, que requer que uma função qualquer seja expressa como a diferença de duas funções positivas
- f = f+ − f−,
em que f+ denota a parte positiva de f e f− a parte negativa.[50]
Espaços vetoriais normados e com produto interno[editar | editar código-fonte]
O processo de "medida" de vetores é feito ao se especificar uma norma, uma função que mede o comprimento de um vetor, ou definindo um produto interno, que mede ângulos entre vetores. Normas e produtos internos são denotados por e , respectivamente. Espaços vetoriais dotados dessa estrutura são denominados espaços vetoriais normados e espaços com produto interno, respectivamente.[51] É possível obter uma norma a partir de um produto interno, definindo-a como .
O espaço de coordenadas Kn pode ser equipado com o produto escalar canônico:
Em R2, isso reflete a noção comum de ângulo entre dois vetores x e y, pela lei dos cossenos:
Por causa disso, dois vetores que satisfaçam são chamados de ortogonais. Uma variante importante do produto interno padrão é usado no espaço de Minkowski; isto é, o espaço R4 dotado do produto de Lorentz
Em contraste com o produto escalar padrão, ele não é positivo definido: também pode assumir valores negativos, como por exemplo para . Isolar a quarta temporada — correspondente ao tempo, em vez das três dimensões espaciais — é útil para o tratamento matemático da relatividade restrita.
Espaços vetoriais topológicos[editar | editar código-fonte]
Questões de convergência são tratadas ao considerar espaços vetoriais que comportem uma topologia compatível, uma estrutura que permite descrever pontos como sendo próximos uns dos outros.[53][54] A compatibilidade significa que a adição e a multiplicação por escalar precisam ser mapas contínuos. Em resumo, se x e y em um espaço vetorial V e a no corpo K variarem por uma quantidade limitada, então x + y e ax variam limitadamente.[nota 8] Para dar sentido em especificar o quanto um escalar varia, o corpo K também precisa carregar uma topologia nesse contexto; opções comuns de corpos são o dos números reais e o dos números complexos.
Nesses espaços vetoriais topológicos é possível considerar série de vetores. A soma infinita
denota o limite das somas parciais finitas correspondentes da sequência (fi)i∈N de elementos de V. Por exemplo, os elementos fi podem ser funções (reais ou complexas) pertencentes a algum espaço funcional V, de modo que a soma infinita seja uma série de funções. O modo de convergência da série é dependente da topologia imposta ao espaço funcional. Nesses casos, convergência pontual e convergência uniforme são dois exemplos proeminentes.
Uma maneira de garantir a existência de limites de certas séries infinitas é restringir o estudo a espaços onde qualquer sequência de Cauchy possui limite; tais espaços vetoriais são denominados completos. Simplificadamente, um espaço vetorial é dito completo contanto que contenha todos os limites necessários; o espaço vetorial dos polinômios nos intervalo unitário [0,1], equipado com a topologia de convergência uniforme, não é completo, pois qualquer função contínua em [0,1] pode ser uniformemente aproximada por uma sequência de polinômios (Teorema de Stone-Weierstrass).[55] Em contraste, o espaço de todas as funções contínuas em [0,1] equipado com a mesma topologia é completo.[56] Uma norma acarreta uma topologia ao definir que uma sequência de vetores vn convirja para v se e somente se
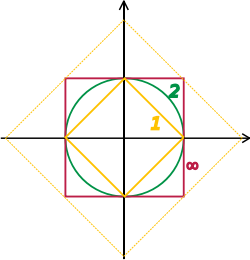
Espaços de Banach e Hilbert são espaços vetoriais topológicos completos cujas topologias são fornecidas, respectivamente, por uma norma e por um produto interno. O estudo deles — uma peça-chave da análise funcional — tem como foco espaços vetoriais de dimensão infinita, já que todas as normas em espaços topológicos de dimensão finita fornecem a mesma noção de convergência.[57] A imagem à direita mostra a equivalência da 1-norma e da ∞-norma no R2: com as "bolas" unitárias englobando-se umas às outras, uma sequência converge a zero em uma norma se e somente se o fizer em uma outra norma. No caso de dimensão infinita, entretanto, em geral existirão topologias não equivalentes, o que faz com que o estudo espaços vetoriais topológicos seja mais rico do que o de espaços vetoriais sem essa estrutura adicional.
De um ponto de vista conceitual, todas as noções relacionadas a espaços vetoriais topológicos devem ser compatíveis com a topologia associada. Por exemplo, ao invés de considerar todas as transformações lineares (também chamadas de funcionais) V → W, exige-se que mapas entre espaços vetoriais topológicos sejam contínuos.[58] Em particular, o espaço dual (topológico) V∗ consiste dos funcionais contínuos V → R (ou para C). O teorema de Hahn-Banach tem por objetivo a separação de subespaços de espaços vetoriais topológicos adequados por funcionais contínuos.[59]
Espaços de Banach[editar | editar código-fonte]
Espaços de Banach, introduzidos por Stefan Banach, são espaços vetoriais normados completos.[60]
Um primeiro exemplo é o espaço vetorial composto de vetores com infinitas entradas reais , cuja -norma dado por
- para e .
As topologias do espaço de dimensão infinita não são equivalentes para diferentes valores de . Como exemplo, a sequência de vetores , em que as primeiras componentes são e as seguintes são , converge para o vetor nulo para , mas não para :
- , mas
De forma mais geral do que sequências de números reais, funções são equipados com uma norma que substitui a soma acima pela integral de Lebesgue
O espaço das funções integráveis em um dado domínio (por exemplo um intervalo) satisfazendo , e equipado com essa norma são chamados de espaços de Lebesgue, denotados como .[nota 9]
Esses espaços são completos.[61] (Se, ao invés disso, a integral de Riemann for utilizada, o espaço não é completo, o que pode ser percebido como uma justificativa para a teoria de integração de Lebesgue.) Concretamente, isso significa que para qualquer sequência de funções do integráveis por Lebesgue com , satisfazendo a condição
- .
Existe uma função pertencente ao espaço vetorial tal que
Impondo condições de limitação não somente à função, mas também às suas derivadas resulta nos espaços de Sobolev.[62]
Espaços de Hilbert[editar | editar código-fonte]

Espaços com produto interno completo são conhecidos como espaços de Hilbert, em homenagem a David Hilbert.[63] O espaço de Hilbert L2(Ω), com produto interno dado por
em que denota o conjugado complexo de g(x),[64][nota 10] é um caso chave.
Por definição, em um espaço de Hilbert qualquer sequência de Cauchy converge para um limite. Dessa forma, encontrar uma sequência de funções fn com propriedades desejáveis que aproxime uma dada função limite torna-se crucial. O início da análise, na forma da aproximação de Taylor, estabeleceu uma aproximação de funções diferenciáveis por polinômios.[65] Pelo teorema de Stone-Weierstrass, toda função contínua em um intervalo [a, b] pode ser aproximada tão bem quanto desejado por um polinômio.[66] Uma técnica de aproximação semelhante feita com funções trigonométricas é comumente chamada de expansão de Fourier, e é muito aplicada em engenharia. De forma mais geral, e mais conceitual, o teorema permite uma descrição simples de quais "funções básicas", ou, no contexto de espaços abstratos de Hilbert, quais vetores básicos são suficientes para gerar o espaço de Hilbert H, no sentido de que o fecho do span desses vetores (isto é, combinações lineares finitas e seus limites) é o espaço inteiro. Tal conjunto de funções é chamada de uma base de H, sua cardinalidade é conhecida como a dimensão do espaço de Hilbert.[nota 11] O teorema não apenas mostra funções adequadas para uma base como suficiente para fazer aproximações, mas também, aliado ao processo de Gram-Schmidt, permite a construção de uma base ortogonal de vetores.[67] Tais bases ortogonais são a generalização em espaços de Hilbert dos eixos de coordenadas em espaços euclidianos, de dimensão finita.
As soluções para várias equações diferenciais podem ser interpretadas em termos de espaços de Hilbert. Por exemplo, muitas áreas da física e da engenharia deparam-se com tais equações e frequentemente soluções com propriedades físicas particulares são utilizadas como funções de uma base, por vezes ortogonal.[68] Na física quântica, a equação de Schrödinger dependente do tempo descreve a mudança de propriedades físicas como função do tempo através de uma equação diferencial parcial, cujas soluções são chamadas de funções de onda.[69] Valores definidos de grandezas físicas como energia e momento correspondem a autovalores de um certo operador diferencial linear e as funções de onda associadas são chamadas de autoestados. O teorema espectral decompõe um operador linear compacto que atua sobre uma função em termos dessas autofunções e desses autovalores.[70]
Propriedades[editar | editar código-fonte]
Terminologia[editar | editar código-fonte]
- Um espaço vetorial sobre o conjuntos dos números reais, é chamado espaço vetorial real.
- Um espaço vetorial sobre o conjuntos dos números complexos, é chamado espaço vetorial complexo.
- Um espaço vetorial com um conceito definido de comprimento, isto é uma norma definida, é chamado espaço vectorial normado.
Tipos de espaços vectoriais[editar | editar código-fonte]
- Espaço Vectorial Euclidiano: É qualquer espaço real que possui um número finito de dimensões e possui uma operação denominada produto interno.[72]
- Espaço de Hilbert: É qualquer espaço vetorial que possui uma operação denominada produto interno e cuja métrica gerada por esse produto interno o torne um espaço completo.
- Espaço normado: É qualquer espaço vetorial que possui uma norma definida
- Espaço de Banach: É um espaço normado completo na métrica gerada por esta norma.
- Espaço vectorial topológico: se existe uma topologia compatível com as operações de espaço vectorial.
Ver também[editar | editar código-fonte]
- Base de um Espaço Vetorial
- Subespaço vetorial
- Módulo (álgebra): a generalização de espaço vetorial, quando o conjunto dos escalares é um anel
- Álgebra sobre um corpo: se existe uma multiplicação de vetores satisfazendo alguns axiomas
Notas
- ↑ Também é comum, especialmente na física, denotar vetores com uma seta superior à letra: .
- ↑ Esse axioma e o próximo se referem a duas operações distintas: a multiplicação por escalar: bv; e a multiplicação do corpo: ab. Eles não afirmam a associatividade de nenhuma das operações. Mais formalmente, a multiplicação por escalar é uma ação monoide do monoide multiplicativo do corpo K sobre o espaço vetorial V.
- ↑ Alguns autores (como Brown 1991) restringem sua atenção aos corpos R ou C, mas a maior parte da teoria permanece inalterada para um corpo qualquer.
- ↑ As funções indicadoras de intervalos (das quais há um número infinito) são linearmente independentes, por exemplo.
- ↑ Ver também o artigo Decomposição de Jordan–Chevalley.
- ↑ Esse é o caso típico quando um espaço vetorial também é considerado como um espaço afim. Neste caso, um subespaço vetorial contém o vetor nulo, enquanto um subespaço afim não o contém necessariamente.
- ↑ Alguns autores (tais como Roman 2005) escolhem começar por essa relação de equivalência e derivar a forma concreta de V/W a partir dela.
- ↑ Essa exigência implica que a topologia acarreta uma estrutura uniforme, Bourbaki 1989, cap. II.
- ↑ A desigualdade triangular para é provida pela desigualdade de Minkowski. Por razões técnicas, no contexto de funções, é preciso identificar funções que concordem em quase todo lugar para se ter uma norma, e não só uma seminorma.
- ↑ Para p ≠2, Lp(Ω) não é um espaço de Hilbert.
- ↑ Uma base de um espaço de Hilbert não é o mesmo que uma base no contexto da álgebra linear, como exposto acima. Por distinção, a última é então chamada de base de Hamel.
Referências
- ↑ Noble & Daniel, 1986, p. 85–86
- ↑ Callioli, Domingues & Costa, 1990, p. 46
- ↑ Callioli, Domingues & Costa, 1990, p. 45
- ↑ Roman 2005, cap. 1, p. 27
- ↑ van der Waerden 1993, Cap. 19
- ↑ Bourbaki 1998, §II.1.1. Bourbaki chamava os homomorfismos de grupo f(a) homotetias.
- ↑ Bourbaki 1969, cap. "Algèbre linéaire et algèbre multilinéaire", pp. 78–91.
- ↑ Bolzano 1804.
- ↑ Möbius 1827.
- ↑ Hamilton 1853.
- ↑ Grassmann 2000.
- ↑ Peano 1888, cap. IX.
- ↑ Banach 1922.
- ↑ Dorier 1995, Moore 1995.
- ↑ Lang 1987, cap. I.1
- ↑ Lang 2002, cap. V.1
- ↑ Lang 1993, cap. XII.3., p. 335
- ↑ Lang 1987, cap. IX.1
- ↑ Lang 1987, cap. VI.3.
- ↑ Roman 2005, Teorema 1.9, p. 43
- ↑ Blass 1984
- ↑ Halpern 1966, pp. 670–673
- ↑ Artin 1991, Teorema 3.3.13
- ↑ Braun 1993, Th. 3.4.5, p. 291
- ↑ Stewart 1975, Proposition 4.3, p. 52
- ↑ Stewart 1975, Teorema 6.5, p. 74
- ↑ Roman 2005, cap. 2, p. 45
- ↑ Lang 1987, cap. IV.4, Corolário, p. 106
- ↑ Lang 1987, Exemplo IV.2.6
- ↑ Lang 1987, cap. VI.6
- ↑ Halmos 1974, p. 28, Ex. 9
- ↑ Lang 1987, Teorema IV.2.1, p. 95
- ↑ Roman 2005, Teorema 2.5 e 2.6, p. 49
- ↑ Lang 1987, cap. V.1
- ↑ Lang 1987, cap. V.3., Corolário, p. 106
- ↑ Lang 1987, Teorema VII.9.8, p. 198
- ↑ Roman 2005, cap. 8, p. 135–156
- ↑ Lang 1987, cap. IX.4
- ↑ Roman 2005, cap. 8, p. 140.
- ↑ Roman 2005, cap. 1, p. 29
- ↑ Roman 2005, cap. 1, p. 35
- ↑ Roman 2005, cap. 3, p. 64
- ↑ Lang 1987, cap. IV.3.
- ↑ Roman 2005, cap. 2, p. 48
- ↑ Mac Lane 1998
- ↑ Roman 2005, cap. 1, pp. 31–32
- ↑ Lang 2002, cap. XVI.1
- ↑ Roman 2005, Teorema 14.3. Ver também Lema de Yoneda.
- ↑ Schaefer & Wolff 1999, pp. 204–205
- ↑ Bourbaki 2004, cap. 2, p. 48
- ↑ Roman 2005, cap. 9
- ↑ Naber 2003, cap. 1.2
- ↑ Treves 1967
- ↑ Bourbaki 1987
- ↑ Kreyszig 1989, §4.11-5
- ↑ Kreyszig 1989, §1.5-5
- ↑ Choquet 1966, Proposição III.7.2
- ↑ Treves 1967, p. 34–36
- ↑ Lang 1983, Cor. 4.1.2, p. 69
- ↑ Treves 1967, cap. 11
- ↑ Treves 1967, Teorema 11.2, p. 102
- ↑ Evans 1998, cap. 5
- ↑ Treves 1967, cap. 12
- ↑ Dennery 1996, p.190
- ↑ Lang 1993, Teorema XIII.6, p. 349
- ↑ Lang 1993, Teorema III.1.1
- ↑ Choquet 1966, Lema III.16.11
- ↑ Kreyszig & 1999 Capítulo 11
- ↑ Griffiths & 1995 Capítulo 1
- ↑ Lang 1993, cap. XVII.3
- ↑ a b Callioli, Domingues & Costa, 1990, p. 50
- ↑ Callioli, Domingues & Costa, 1990, p. 159
Bibliografia[editar | editar código-fonte]
- Callioli, Carlos A.; Domingues, Hygino H.; Costa, Roberto C. F. (1990). Álgebra Linear e Aplicações (PDF) 6 ed. São Paulo: Atual. ISBN 9788570562975
- Noble, Ben; James W. Daniel (1986). Álgebra Linear Aplicada. Rio de Janeiro: Prentice-Hall do Brasil. ISBN 9788570540225
Álgebra[editar | editar código-fonte]
- Artin, Michael (1991). Algebra (em inglês). [S.l.]: Prentice Hall. ISBN 978-0-89871-510-1
- Blass, Andreas (1984), «Existence of bases implies the axiom of choice», Axiomatic set theory (Boulder, Colorado, 1983), Contemporary Mathematics, 31, Providence, R.I.: American Mathematical Society, p. 31–33, MR 763890
- Brown, William A. (1991), Matrices and vector spaces, ISBN 978-0-8247-8419-5, New York: M. Dekker
- Lang, Serge (1987), Linear algebra, ISBN 978-0-387-96412-6, Berlin, New York: Springer-Verlag
- Predefinição:Lang Algebra
- Mac Lane, Saunders (1999), Algebra, ISBN 978-0-8218-1646-2 3rd ed. , p. 193–222
- Meyer, Carl D. (2000), Matrix Analysis and Applied Linear Algebra, ISBN 978-0-89871-454-8, SIAM
- Roman, Steven (2005), Advanced Linear Algebra, ISBN 978-0-387-24766-3, Graduate Texts in Mathematics, 135 2nd ed. , Berlin, New York: Springer-Verlag
- Spindler, Karlheinz (1993), Abstract Algebra with Applications: Volume 1: Vector spaces and groups, ISBN 978-0-8247-9144-5, CRC
- van der Waerden, Bartel Leendert (1993), Algebra, ISBN 978-3-540-56799-8 (em alemão) 9th ed. , Berlin, New York: Springer-Verlag
Análise[editar | editar código-fonte]
- Bourbaki, Nicolas (1987), Topological vector spaces, ISBN 978-3-540-13627-9, Elements of mathematics, Berlin, New York: Springer-Verlag
- Bourbaki, Nicolas (2004), Integration I, ISBN 978-3-540-41129-1, Berlin, New York: Springer-Verlag
- Braun, Martin (1993), Differential equations and their applications: an introduction to applied mathematics, ISBN 978-0-387-97894-9, Berlin, New York: Springer-Verlag
- BSE-3 (2001), «Tangent plane», in: Hazewinkel, Michiel, Enciclopédia de Matemática, ISBN 978-1-55608-010-4 (em inglês), Springer
- Choquet, Gustave (1966), Topology, Boston, MA: Academic Press
- Dennery, Philippe; Krzywicki, Andre (1996), Mathematics for Physicists, ISBN 978-0-486-69193-0, Courier Dover Publications
- Dudley, Richard M. (1989), Real analysis and probability, ISBN 978-0-534-10050-6, The Wadsworth & Brooks/Cole Mathematics Series, Pacific Grove, CA: Wadsworth & Brooks/Cole Advanced Books & Software
- Dunham, William (2005), The Calculus Gallery, ISBN 978-0-691-09565-3, Princeton University Press
- Evans, Lawrence C. (1998), Partial differential equations, ISBN 978-0-8218-0772-9, Providence, R.I.: American Mathematical Society
- Folland, Gerald B. (1992), Fourier Analysis and Its Applications, ISBN 978-0-534-17094-3, Brooks-Cole
- Gasquet, Claude; Witomski, Patrick (1999), Fourier Analysis and Applications: Filtering, Numerical Computation, Wavelets, ISBN 978-0-387-98485-8, Texts in Applied Mathematics, New York: Springer-Verlag
- Ifeachor, Emmanuel C.; Jervis, Barrie W. (2001), Digital Signal Processing: A Practical Approach, ISBN 978-0-201-59619-9 2nd ed. , Harlow, Essex, England: Prentice-Hall (publicado em 2002)
- Krantz, Steven G. (1999), A Panorama of Harmonic Analysis, ISBN 978-0-88385-031-2, Carus Mathematical Monographs, Washington, DC: Mathematical Association of America
- Kreyszig, Erwin (1988), Advanced Engineering Mathematics, ISBN 978-0-471-85824-9 6th ed. , New York: John Wiley & Sons
- Kreyszig, Erwin (1989), Introductory functional analysis with applications, ISBN 978-0-471-50459-7, Wiley Classics Library, New York: John Wiley & Sons, MR 992618
- Lang, Serge (1983), Real analysis, ISBN 978-0-201-14179-5, Addison-Wesley
- Lang, Serge (1993), Real and functional analysis, ISBN 978-0-387-94001-4, Berlin, New York: Springer-Verlag
- Loomis, Lynn H. (1953), An introduction to abstract harmonic analysis, Toronto-New York–London: D. Van Nostrand Company, Inc., p. x+190, hdl:2027/uc1.b4250788

- Schaefer, Helmut H.; Wolff, M.P. (1999), Topological vector spaces, ISBN 978-0-387-98726-2 2nd ed. , Berlin, New York: Springer-Verlag
- Treves, François (1967), Topological vector spaces, distributions and kernels, Boston, MA: Academic Press
Referências históricas[editar | editar código-fonte]
- Banach, Stefan (1922), «Sur les opérations dans les ensembles abstraits et leur application aux équations intégrales (On operations in abstract sets and their application to integral equations)» (PDF), Fundamenta Mathematicae, ISSN 0016-2736 (em francês), 3: 133–181, doi:10.4064/fm-3-1-133-181
- Bolzano, Bernard (1804), Betrachtungen über einige Gegenstände der Elementargeometrie (Considerations of some aspects of elementary geometry) (em alemão)
- Bourbaki, Nicolas (1969), Éléments d'histoire des mathématiques (Elements of history of mathematics) (em francês), Paris: Hermann
- Dorier, Jean-Luc (1995), «A general outline of the genesis of vector space theory», Historia Mathematica, 22 (3): 227–261, MR 1347828, doi:10.1006/hmat.1995.1024

- Fourier, Jean Baptiste Joseph (1822), Théorie analytique de la chaleur (em francês), Chez Firmin Didot, père et fils
- Grassmann, Hermann (1844), Die Lineale Ausdehnungslehre - Ein neuer Zweig der Mathematik (em alemão), O. Wigand, reprint: Hermann Grassmann. Translated by Lloyd C. Kannenberg. (2000), Kannenberg, L.C., ed., Extension Theory, ISBN 978-0-8218-2031-5, Providence, R.I.: American Mathematical Society
- Hamilton, William Rowan (1853), Lectures on Quaternions, Royal Irish Academy
- Möbius, August Ferdinand (1827), Der Barycentrische Calcul : ein neues Hülfsmittel zur analytischen Behandlung der Geometrie (Barycentric calculus: a new utility for an analytic treatment of geometry) (em alemão), arquivado do original em 23 de novembro de 2006
- Moore, Gregory H. (1995), «The axiomatization of linear algebra: 1875–1940», Historia Mathematica, 22 (3): 262–303, doi:10.1006/hmat.1995.1025

- Peano, Giuseppe (1888), Calcolo Geometrico secondo l'Ausdehnungslehre di H. Grassmann preceduto dalle Operazioni della Logica Deduttiva (em italiano), Turin
Referências extras[editar | editar código-fonte]
- Ashcroft, Neil; Mermin, N. David (1976), Solid State Physics
 , ISBN 978-0-03-083993-1, Toronto: Thomson Learning
, ISBN 978-0-03-083993-1, Toronto: Thomson Learning - Atiyah, Michael Francis (1989), K-theory, ISBN 978-0-201-09394-0, Advanced Book Classics 2nd ed. , Addison-Wesley, MR 1043170
- Bourbaki, Nicolas (1998), Elements of Mathematics : Algebra I Chapters 1-3, ISBN 978-3-540-64243-5, Berlin, New York: Springer-Verlag
- Bourbaki, Nicolas (1989), General Topology. Chapters 1-4, ISBN 978-3-540-64241-1, Berlin, New York: Springer-Verlag
- Coxeter, Harold Scott MacDonald (1987), Projective Geometry, ISBN 978-0-387-96532-1 2nd ed. , Berlin, New York: Springer-Verlag
- Eisenberg, Murray; Guy, Robert (1979), «A proof of the hairy ball theorem», The American Mathematical Monthly, 86 (7): 572–574, JSTOR 2320587, doi:10.2307/2320587
- Eisenbud, David (1995), Commutative algebra, ISBN 978-0-387-94269-8, Graduate Texts in Mathematics, 150, Berlin, New York: Springer-Verlag, MR 1322960
- Goldrei, Derek (1996), Classic Set Theory: A guided independent study, ISBN 978-0-412-60610-6 1st ed. , London: Chapman and Hall
- Griffiths, David J. (1995), Introduction to Quantum Mechanics, ISBN 978-0-13-124405-4, Upper Saddle River, NJ: Prentice Hall
- Halmos, Paul R. (1974), Finite-dimensional vector spaces, ISBN 978-0-387-90093-3, Berlin, New York: Springer-Verlag
- Halpern, James D. (junho de 1966), «Bases in Vector Spaces and the Axiom of Choice», Proceedings of the American Mathematical Society, 17 (3): 670–673, JSTOR 2035388, doi:10.2307/2035388

- Hughes-Hallett, Deborah; McCallum, William G.; Gleason, Andrew M. (2013), Calculus : Single and Multivariable, ISBN 978-0470-88861-2 6 ed. , John Wiley & Sons
- Husemoller, Dale (1994), Fibre Bundles, ISBN 978-0-387-94087-8 3rd ed. , Berlin, New York: Springer-Verlag
- Jost, Jürgen (2005), Riemannian Geometry and Geometric Analysis, ISBN 978-3-540-25907-7 4th ed. , Berlin, New York: Springer-Verlag
- Kreyszig, Erwin (1991), Differential geometry, ISBN 978-0-486-66721-8, New York: Dover Publications, p. xiv+352
- Kreyszig, Erwin (1999), Advanced Engineering Mathematics, ISBN 978-0-471-15496-9 8th ed. , New York: John Wiley & Sons
- Luenberger, David (1997), Optimization by vector space methods, ISBN 978-0-471-18117-0, New York: John Wiley & Sons
- Mac Lane, Saunders (1998), Categories for the Working Mathematician, ISBN 978-0-387-98403-2 2nd ed. , Berlin, New York: Springer-Verlag
- Misner, Charles W.; Thorne, Kip; Wheeler, John Archibald (1973), Gravitation, ISBN 978-0-7167-0344-0, W. H. Freeman
- Naber, Gregory L. (2003), The geometry of Minkowski spacetime, ISBN 978-0-486-43235-9, New York: Dover Publications, MR 2044239
- Schönhage, A.; Strassen, Volker (1971), «Schnelle Multiplikation großer Zahlen (Fast multiplication of big numbers)», Computing, ISSN 0010-485X (em alemão), 7 (3–4): 281–292, doi:10.1007/bf02242355
- Spivak, Michael (1999), A Comprehensive Introduction to Differential Geometry (Volume Two), Houston, TX: Publish or Perish
- Stewart, Ian (1975), Galois Theory, ISBN 978-0-412-10800-6, Chapman and Hall Mathematics Series, London: Chapman and Hall
- Varadarajan, V. S. (1974), Lie groups, Lie algebras, and their representations, ISBN 978-0-13-535732-3, Prentice Hall
- Wallace, G.K. (fevereiro de 1992), «The JPEG still picture compression standard» (PDF), IEEE Transactions on Consumer Electronics, ISSN 0098-3063, 38 (1): xviii–xxxiv, CiteSeerX 10.1.1.318.4292
 , doi:10.1109/30.125072
, doi:10.1109/30.125072 - Predefinição:Weibel IHA
Ligações externas[editar | editar código-fonte]
- Livro Álgebra Vetorial e Geometria Analítica: Livro do Prof. Jacir J. Venturi, de 242 páginas, disponível na íntegra para acesso gratuito.
















































































