Teorema do valor médio

Cálculo
Teorema fundamental Limite de funções Continuidade Teorema do valor médio Teorema de Rolle
Cálculo Definições Derivada Diferencial Diferencial de uma função Generalizações da derivada Conceitos Notações para diferenciação Segunda derivada Terceira derivada Mudança de variáveis Derivação implícita Taxas relativas Teorema de Taylor Regras de derivação Somas Produto Regra da cadeia Potências Quocientes Fórmula de Faà di Bruno
Cálculo integral Tábua de integrais Definições Primitiva Integral Integral imprópria Integral de Riemann Integral de Lebesgue Contour integral Integração por partes discs cylindrical shells substitution substituição trigonométrica Frações parciais changing order reduction formulae
Série Geométrica Arithmetico-geometric Harmônica Alternating Potências Binomial Taylor Testes de convergência Teste da divergência Razão Raiz Integral Comparação direta Limit comparison Série alternada Cauchy condensation Dirichlet Abel
Cálculo vetorial Gradiente Divergência Rotacional Laplaciano Gradient theorem Teorema de Green Teorema de Stokes Teorema da divergência Directional derivative
Cálculo com múltiplas variáveis Formalismo Matriz Tensor Exterior Geometric Definições Derivada parcial Integral múltipla Integral de linha Integral de superfície Integral de volume Matriz jacobiana
Cálculo especializado Cálculo de variações Fracional Malliavin Estocástico

O teorema do valor médio

Em matemática, o teorema do valor médio (também conhecido como Teorema de Lagrange) afirma que dada uma função contínua f definida num intervalo fechado [a,b] e diferenciável em (a,b), existe algum ponto c em (a,b) tal que :$f'(c)={\frac {f(b)-f(a)}{b-a}}\cdot$

Geometricamente, isto significa que a tangente ao gráfico de f no ponto de abcissa c é paralela à secante que passa pelos pontos de abcissas a e b

O teorema do valor médio também tem uma interpretação em termos físicos: se um objeto está em movimento e se a sua velocidade média é $v$, então, durante esse percurso (intervalo [a,b]), há um instante (ponto c) em que a velocidade instantânea também é $v$.

Demonstração

Seja

${\begin{array}{rccc}g\colon &[a,b]&\longrightarrow &\mathbb {R} \\&x&\mapsto &f(x)-f(a)-{\frac {f(b)-f(a)}{b-a}}(x-a).\end{array}}$

Então $g$ também é contínua em $[a,b]$ e derivável em $(a,b)$. Além disso, $g(a)=g(b)=0$. Logo, pelo teorema de Rolle, existe algum $c$ ∈ $(a,b)$ tal que $g'(c)=0$. Mas

${\begin{aligned}g'(c)=0&\Longleftrightarrow f'(c)-{\frac {f(b)-f(a)}{b-a}}=0\\&\Longleftrightarrow f'(c)={\frac {f(b)-f(a)}{b-a}}\cdot \end{aligned}}$

Funções com Valores Vetoriais

Se $f$ for uma função contínua de $[a,b]$ em R$^{n}$ que seja derivável em $(a,b)$, então já não é verdade que existe necessariamente algum $c$ ∈ $(a,b)$ tal que

$f'(c)={\frac {f(b)-f(a)}{b-a}}\cdot$

Considere-se, por exemplo, a função $f$ de $[0,2\pi ]$ em R$^{2}$ definida por

$f(x)=(\cos(x),\operatorname {sen} (x))$.

Então

${\frac {f(2\pi )-f(0)}{2\pi -0}}=(0,0),$

mas

$(\forall x\in (0,2\pi )):f'(x)=(-\operatorname {sen} (x),\cos(x))\neq (0,0).$

No entanto, é verdade que existe sempre algum $c$ ∈ $(a,b)$ tal que

${\frac {\|f(b)-f(a)\|}{b-a}}\leqslant \|f'(c)\|.$

Isto pode ser demonstrado do seguinte modo. Seja $v$ ∈ R$^{n}$ um vector de norma 1 tal que

$\langle v,f(b)-f(a)\rangle =\|f(b)-f(a)\|$

e seja

${\begin{array}{rccc}g\colon &[a,b]&\longrightarrow &\mathbb {R} \\&x&\mapsto &\langle v,f(x)-f(a)\rangle .\end{array}}$

Então $g$ é contínua em $[a,b]$ e derivável em $(a,b)$, pelo que existe algum $c$ ∈ $(a,b)$ tal que

$g'(c)={\frac {g(b)-g(a)}{b-a}}\Longleftrightarrow \langle v,f'(c)\rangle =\left\langle v,{\frac {f(b)-f(a)}{b-a}}\right\rangle ={\frac {\|f(b)-f(a)\|}{b-a}},$

pelo que, pela desigualdade de Cauchy-Schwarz,

${\frac {\|f(b)-f(a)\|}{b-a}}={\bigl |}\langle v,f'(c)\rangle {\bigr |}\leqslant \|v\|.\|f'(c)\|=\|f'(c)\|.$

Generalização: Teorema de Cauchy

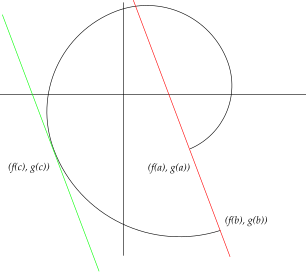
Significado geométrico do teorema de Cauchy.

Um resultado mais geral é o Teorema de Cauchy, que afirma que se f e g são funções contínuas de [a,b] em R que são deriváveis em (a,b), então existe algum c ∈ (a,b) tal que

$(f(b)-f(a))g'(c)=(g(b)-g(a))f'(c).$

É uma generalização do teorema de Lagrange pois, se se tomar g(x) = x, isto significa

$f(b)-f(a)=(b-a)f'(c)\Leftrightarrow {\frac {f(b)-f(a)}{b-a}}=f'(c).$

O Teorema de Cauchy pode ser demonstrado considerando a função h de [a,b] em R definida por

$h(x)=(f(b)-f(a))(g(x))-(g(b)-g(a))(f(x)).$

Então h é contínua, é derivável em (a,b) e h(a) = h(b), pelo que existe algum c ∈ (a,b) tal que

${\begin{aligned}h'(c)=0&\Leftrightarrow (f(b)-f(a))g'(c)-(g(b)-g(a))f'(c)=0\\&\Leftrightarrow (f(b)-f(a))g'(c)=(g(b)-g(a))f'(c).\end{aligned}}$

Naturalmente, o Teorema de Cauchy não tem interesse caso f(a) = f(b) e g(a) = g(b). Caso contrário, o significado do teorema de Cauchy é: se se considerar a curva

${\begin{array}{ccc}[a,b]&\longrightarrow &\mathbb {R} ^{2}\\x&\mapsto &{\bigl (}f(x),g(x){\bigr )},\end{array}}$

então o declive de recta definida por (f(a),g(a)) e por (f(b),g(b)) é igual ao declive da tangente à curva em algum ponto.

Ver também

• Teorema da velocidade média
• Teorema de Rolle