Energia de Fermi
As referências deste artigo necessitam de formatação. (Agosto de 2013) |
A Energia de Fermi é a energia do nível ocupado mais energético em um sistema quântico fermiônico à temperatura de zero absoluto. A definição estende-se também a sistemas acima do zero absoluto, caso em que a energia de fermi corresponde à energia obtida mediante uma média das energias dos níveis quânticos com probabilidade de ocupação - devido à agitação térmica - diferentes da unidade, cada qual ponderado pela respectiva probabilidade de ocupação. Associa-se via de regra à energia de fermi a notação EF, e a nomenclatura retrata nítida homenagem ao físico ítalo-americano Enrico Fermi.
Introdução[editar | editar código-fonte]
Contexto geral[editar | editar código-fonte]
Esta seção não cita fontes confiáveis. (Julho de 2022) |
A energia de Fermi é importante na hora de entender o comportamento de partículas fermiônicas, como por exemplo os elétrons. Os férmions são partículas de spin semi-inteiro para as quais verifica-se a validade do princípio de exclusão de Pauli - que dita que dois férmions idênticos não podem ocupar simultaneamente o mesmo estado quântico. Desta maneira, quando um sistema possui vários elétrons, estes ocuparão níveis de energia maiores a medida que os níveis inferiores estejam preenchidos.
A energia de Fermi é um conceito que tem muitas aplicações na teoria dos orbitais atômicos, no comportamento dos semicondutores e na física do estado sólido em geral.
Em física do estado sólido a superficie de Fermi é a superficie no espaço de momentos na qual a energia de excitação total se iguala à energia de Fermi. Esta superfície pode ter uma topologia não trivial. Simplificadamente se pode dizer que a superfície de Fermi divide os estados electrônicos ocupados dos que permanecem livres.
Enrico Fermi e Paul Dirac, derivaram as estatísticas de Fermi-Dirac. Estas estatísticas permitem predizer o comportamento de sistemas formados por um grande número de elétrons, especialmente em corpos sólidos.
A energia de Fermi de um gás de Fermi (ou gás de elétrons livres) não relativista tridimensional se pode relacionar com o potencial químico através da equação:
onde εF é a energia de Fermi, k é a constante de Boltzmann e T é a temperatura. Portanto, o potencial químico é aproximadamente igual a a energia de Fermi à temperaturas muito inferiores a uma energia característica denominada Temperatura de Fermi, εF/k. Esta temperatura característica é da ordem de 105K para um metal a uma temperatura ambiente de (300 K), pelo que a energia de Fermi e o potencial químico são essencialmente equivalentes. Este é um detalhe significativo dado que o potencial químico, e não a energia de Fermi, é quem aparece nas estatísticas de Fermi-Dirac.
Contexto avançado[editar | editar código-fonte]
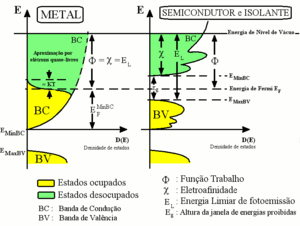
Elétrons são férmions, ou seja, são partículas regidas pela estatística de Fermi. Nesta estatística, um dado estado quântico pode ser ocupado por no máximo um e não mais que um férmion, e portanto a máxima probabilidade de ocupação de um dado estado quântico é um. Os elétrons situados dentro da amostra estão confinados por um potencial atrativo exercido pelos íons positivos da rede. Conforme mostrado pela mecânica quântica, potenciais confinantes apresentam níveis de energias discretos. No caso dos átomos isto se reflete nos tão conhecidos níveis atômicos de energia e no caso dos sólidos cristalinos, a aproximação entre os átomos leva a um agrupamento dos estados em bandas de energia. Estas bandas são vistas nas relações de dispersão para os sólidos como sendo as regiões de energia permitidas para os elétrons, separadas umas das outras por janelas de energias proibidas (ou “gaps”).
Rigorosamente falando,[1] a energia do nível de Fermi é definida em sistemas à temperatura de zero absoluto. Nesse caso, a energia do nível de Fermi é a energia do nível mais energético ocupado, visto que nessa temperatura todos os níveis com energia menor que a energia do nível de Fermi estariam ocupados (probabilidade igual a 1) e todos os níveis com energia acima, desocupados (probabilidade de ocupação nula). Para sistemas em temperaturas não nulas, não temos mais uma transição abrupta da probabilidade de ocupação, e sim uma probabilidade dada pela distribuição de Fermi-Dirac. Considera-se então como a energia do nível de Fermi a energia obtida pela média aritmética ponderada das energias de cada estado energético afetado pela excitação térmica (estados com probabilidades de ocupação diferentes de 1 ou 0) pesadas cada qual pela respectiva probabilidade de ocupação do estado associado. O denominador desta média será obviamente o número de estados envolvidos no processo. Repare que em acordo com a estatística de Fermi, dentre os referidos estados os menos energéticos têm probabilidade de ocupação maior do que aqueles mais energéticos. Para aproximação de elétrons livres a densidade de estados cresce com a raiz quadrada da energia, resultando em uma parábola no gráfico de energia x densidade de estados. Em semicondutores e isolantes esta dependência pode ser bem mais complicada.
Outra definição equivalente implica dizer que a energia de Fermi corresponde ao potencial eletroquímico do sistema na temperatura de zero absoluto. Uma extensão a temperaturas maiores é evidente, e a energia de Fermi corresponde assim ao potencial eletroquímico do sistema na temperatura considerada. A energia de Fermi expressa, portanto, qual seria a variação da energia interna total do sólido, considerado sempre como sistema isolado e em equilíbrio termodinâmico, caso um elétron fosse dele removido. Sendo ENtotal a energia total do sistema no estado neutro, em seu equilíbrio termodinâmico, e EN-1total a energia total do sistema também em seu novo equilíbrio termodinâmico mas após a remoção do elétron, temos que:
- EF = ENtotal - EN-1total
Nas definições acima, o nível de referência é o nível de menor energia disponível aos N elétrons, e a remoção de um elétron provoca, então, a redução da energia do sistema. Neste referencial a energia de Fermi é, portanto, positiva, bem como o potencial eletroquímico.
Quando dois materiais diferentes são colocados em contato, a condição de equilíbrio termodinâmico exige que as suas energias de Fermi sejam iguais. Se as energias de Fermi fossem diferentes, a passagem de um elétron do sólido com maior energia de Fermi para o sólido com menor energia de Fermi resultaria em uma diminuição da energia total do sistema e o sistema composto não estaria, então, em sua configuração de equilíbrio, a de mínima energia, conforme exigido pelas leis da termodinâmica. Este fato dá origem a um fenômeno conhecido por diferença de potencial de contato que encontra diversas aplicações práticas, a saber na eletrônica de estado sólido (junção PN) e no uso do metal de sacrifício em navios.
Ilustração do conceito para compartimento monodimensional quadrado[editar | editar código-fonte]
Esta seção não cita fontes confiáveis. (Julho de 2022) |
A monodimensional compartimento quadrado infinito é um modelo para uma caixa mono dimensional. É um sitema modelo padrão em mecânica quântica para o qual a solução para uma partícula isolada é bem conhecido. Os níveis são marcados por um único número quântico n e as energias são dadas por
- .
Suponha-se agora que em vez de uma partícula nesta caixa nós temos N partículas na caixa e que estas partículas são férmions com spin 1/2. Então somente duas partículas podem ter a mesma energia i.e. duas partículas podem ter a energia de , ou duas partículas podem ter energia e assim por diante. A razão que duas partículas podem ter a mesma energia é que uma partícula de spin 1/2 pode ter um spin de 1/2 (spin "acima") ou um spin de -1/2 (spin "abaixo"), conduzindo a dois estadois para cada nível de energia. Quando nós olhamos na energia total deste sistema, a configuração para as quais a energia total é a menor (o estado fundamental), é a configuração onde todos os níveis de energia acima de n=N/2 estão ocupados e todos os níveis mais altos estão vazios. A energia de Fermi é consequentemente
- .
O caso tridimensional[editar | editar código-fonte]
Esta seção não cita fontes confiáveis. (Julho de 2022) |
O caso tridimensional isotrópico é conhecido como a esfera de Fermi.
Deixe-nos agora considerar uma caixa cúbica tridimensional que tem um lado de comprimento L (ver compartimento quadrado infinito). Este torna-se uma muito boa aproximação para descrever elétrons em um metal.
Os estados agora são marcados po três números quânticos nx, ny, e nz. As energias da partícula isolada são
- nx, ny, nz são inteiros positivos.
Existem múltiplos estados com a mesma energia, por exemplo . Agora deixemos colocar-se N férmions não interativos de spin 1/2 nesta caixa. Para calcular a energia de Fermi, nós veremos no caso de que N é grande.
Se nós introduzios um vetor então cada estado quântico corresponde a um ponto num "n-espaço" com energia
- .
O número de estados com energia menor que Ef é igual ao número de estados que residem em uma esfera de raio na região do "n-espaço" onde nx, ny, nz são positivos. No estado básico este número iguala o número de férmions no sistema.

o fator é de dois é novamente porque são doisestados de spin, o fator de 1/8 é porque somente 1/8 da esfera repousa na região onde todos n são positivos.
Nós obtemos
então a energia de Fermi é dada por
Tais resultados em uma relação entre a energia de Fermi e o número de partículas por volume (quando nós substituímos L2 com V2/3):
A energia de Fermi total de um esfera de fermi de férmions é dada por
Energia de Fermi total:
Integração por substituição:
A eliminação de em favor de :
Energias de Fermi típicas[editar | editar código-fonte]
Anãs brancas[editar | editar código-fonte]
Esta seção não cita fontes confiáveis. (Julho de 2022) |
Estrelas conhecidas como anãs brancas tem massa comparável a nosso Sol, mas têm um raio aproximadamente 100 vezes menor. As alta densidades implicam que os elétrons estão não mais ligados a um núcleo isolado e formam um gás de elétrons degenerado. Os números da densidade de elétrons em uma anã branca são da ordem de 1036 elétrons/m3. Isto significa que sua energia de Fermi é:
Núcleos[editar | editar código-fonte]
Outro exemplo típico é as partículas em um núcleo de um átomo. Os núcleons de um núcleo atômico pode ser tratado, assim, como um gás de Fermi e como tal, modelado.[2]
O raio do núcleo é aproximadamente[3]:
- onde A é o número de núcleons.
O número densidade de núcleons em um núcleo é conseqüentemente:
Agora, como a energia de fermi somente aplica-se a férmions de mesmo tipo, deve-se dividir esta energia por dois. Isto por causa da presença de nêutrons que não afetam a energia de Fermi dos prótons no núcleo, e vice versa.[4][5][6]
Assim a energia de fermi de um núcleo é dada por:
O raio do núcleo admite desvios em torno do valor mencionado acima, então um típico valor para a energia de Fermi normalmente dada é 38 MeV.
Referências
- ↑ Para a presente definição de energia de Fermi e suas aplicações em física do estado sólido e em técnicas de análise como a Espectroscopia de fotoelétrons excitados por raios X consulte Carvalho, Lauro Chieza de - dissertação [1]
- ↑ Theoretical Nuclear Physics. John M. Blatt and Victor F. Weisskopf. New York: Wiley; London: Chapman & Hall, 1952.
- ↑ 8. Models of the nucleus - 8.1 Fermi-gas model - www.e18.physik.tu-muenchen.de Arquivado em 13 de outubro de 2017, no Wayback Machine. (em inglês)
- ↑ Física Atómica e Nuclear – Capítulo 8. Modelos Nucleares - w3.ualg.pt
- ↑ The Fermi gas model - www.phy.uct.ac.za Arquivado em 6 de junho de 2008, no Wayback Machine. (em inglês)
- ↑ Fermi Gas Model - physics.valpo.edu (em inglês)
Bibliografia[editar | editar código-fonte]
- Kroemer, Herbert; Kittel, Charles (1980). Thermal Physics (2nd ed.). [S.l.]: W. H. Freeman Company. ISBN 0-7167-1088-9
- Tabela das energias de Fermi, velocidades, e temperaturas para vários elementos. (em inglês)
- uma discussão sobre gases de fermi e temperaturas de Fermi. (em inglês)
- Carvalho, Lauro Chieza de - Estudo das Estruturas Fe:GaAs e Fe:Cs:GaAs por Espectroscopia de Fotoelétrons Excitados por Raios X - Universidade Federal de Minas Gerais - ICEx - 11 de julho de 2005 [2].

![{\displaystyle \mu =\epsilon _{F}\left[1-{\frac {\pi ^{2}}{12}}\left({\frac {kT}{\epsilon _{F}}}\right)^{2}+{\frac {\pi ^{4}}{80}}\left({\frac {kT}{\epsilon _{F}}}\right)^{4}+...\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/80462a105fffc6a82aab94ce41c209b37211f333)



















![{\displaystyle E_{t}={\frac {3}{5}}N_{0}E_{f}={\frac {3}{5}}N_{0}\left[{\frac {\hbar ^{2}\pi ^{2}}{2mL^{2}}}\left({\frac {3N_{0}}{\pi }}\right)^{2/3}\right]={\frac {3^{\frac {5}{3}}\pi ^{\frac {4}{3}}\hbar ^{2}}{10mL^{2}}}N_{0}^{\frac {5}{3}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ac09bbd4ff9cff66bb792332332a91f88d8d6a79)








