Força fictícia

Uma força fictícia, força d'Alembert, ou ainda força inercial,é um efeito percebido por um observador estacionário em relação a um sistema de referência não inercial quando analisa seu sistema como se fosse um sistema de referência inercial. A força fictícia é representada matematicamente como um vetor força calculável a partir da massa dos corpos sobre a qual atua e a aceleração em relação ao sistema de referência não inercial.

Um referencial inercial é qualquer sistema de referência que se encontra em movimento retilíneo uniforme ou em repouso em relação ao espaço absoluto, dessa forma, qualquer sistema em que não é possível comprovar os fenômenos realizados pelas forças sem um causador visível, são denominadas forças inerciais ou forças fictícias. Consequentemente, as três leis de Newton não podem ser aplicadas aos referenciais não inerciais, que são sistemas de referência acelerados. Para estudar o movimento de um corpo do ponto de vista de um referencial não inercial, levamos em consideração os efeitos causados pelas forças fictícias.

Para entender melhor sobre conceito de forças fictícias podemos utilizar um exemplo comum de quando se trata do assunto:

Um passageiro sentado no banco de um carro que está se movimentando  em linha reta que de repente freia bruscamente projetando o passageiro para frente. Observando o respectivo exemplo, poderíamos dizer que se parecem com forças reais, porém não se encaixam no sistema de referencial inercial, não sendo forças gravitacionais, nucleares e nem eletromagnéticas. Se analisarmos o movimento do passageiro ligando o sistema estacionário ao chão, a força fictícia não pode ser aplicada. Entretanto, se observarmos o evento da perspectiva do passageiro, em movimento em um sistema acelerado, a força fictícia ou força inercial se manifesta.

Força fictícia na Terra

A superfície da Terra é um sistema de referência rotativo. Para resolver problemas de mecânica clássica exatamente em um quadro de referência ligado à Terra, devem ser introduzidas três forças fictícias: a força de Coriolis, a força centrífuga e a força de Euler. A força de Euler é geralmente ignorada, pois as variações na velocidade angular da superfície rotativa da Terra são geralmente insignificantes. As outras duas forças fictícias são fracas se relacionadas com outras forças tipicas da vida cotidiana, porém podem ser detectadas sob uma situação atenta.

Um exemplo interessante é o Pêndulo de Foucault, utilizado para demostrar o movimento de rotação da Terra. Se for colocado no Polo Norte, o seu plano de oscilação será sempre o mesmo em relação a um sistema inercial com o centro no Sol. Como a Terra gira em torno do próprio eixo, que passa pelos polos, um sistema de referência ligado à Terra observa o plano de oscilação girar. Uma vez que não existe força real atuando para que o pêndulo gire, concluímos que esse referencial não é inercial.

Exemplos de forças fictícias

Aceleração em movimento linear

O exemplo utilizado para introduzir o assunto "força fictícia" apontado acima se encaixa perfeitamente quando se fala de força fictícia em uma aceleração linear. Para entender melhor o fenômeno vamos relembrar um pouco o modelo apresentado.

Uma pessoa está dentro de um carro, quando o mesmo freia, a pessoa se sente lançada para frente do veiculo. O mesmo acontece quando o carro acelera fazendo com que o passageiro seja empurrado de volta ao assento, uma força fictícia atua impulsionando a pessoa para trás, tendo em vista que não há forças físicas agindo para que isso aconteça. Outro exemplo interessante também usando um carro, que neste caso está acelerado desde o inicio da sua trajetória, o observador que está fora do carro está em um sistema de referencial inercial e interpreta a aceleração do carro como uma força direta. Portanto, o observador que está dentro do carro tende a usar o carro como seu sistema de referência, como se ainda estivesse em repouso, porém como está acelerado perceberá movimentos diferentes do observador que realmente está em repouso.

Movimento circular: Força de Coriolis e Força centrífuga

Ver artigos principais: Força inercial de Coriolis e Força inercial centrífuga

Direção e sentido da força de Coriolis para uma partícula que se move na direção radial em um disco em rotação.

As forças em movimento circular são as mais populares quando se trata de forças fictícias, conforme citado anteriormente são a força de Coriolis e a força centrifuga.

Força de Coriolis

A força de Coriolis, ocorre em um referencial rotativo, porém diferentemente da força inercial centrífuga a força de coriolis atua isoladamente sobre os corpos, que se movimentam em relação ao sistema fixo à Terra em direção perpendicular ao movimento, modificando somente a sua direção. O conceito da força de coriolis pode ser melhor compreendido se observamos o fato do movimento atmosférico ( desempenhando o mesmo papel de um corpo) que gira juntamente com a Terra, esse movimento fica mais evidente aos olhos humanos através de alguns fenômenos naturais, o que torna a força de Coriolis fundamental para a descrição de correntes de convecção em fluidos, que surgem em fenômenos meteorológicos, tais como circulação atmosférica de larga escala e circulação de brisas e correntes marítimas, também são encarregadas pelo sentido ( horário ou anti-horário), nos quais giram os ciclones no Hemisfério Norte e Sul. Observando o fato da Terra ser um referencial em rotação podemos considerar que a força de coriolis age sobre os objetos em sua superfície, ainda que nem sempre esses efeitos sejam perceptíveis Em vista disso, a força de coriolis apenas se desempenha quando o corpo também se move no referencial rotativo, ou seja, dependendo da velocidade do corpo no sistema, caso o corpo esteja parado as forças de coriolis são nulas, portanto, as únicas forças fictícias atuando no sistema (onde $v=0$) são as forças centrifugas. Vale ressaltar que, conforme foi mencionado anteriormente, a força de coriolis se tornou uma prova da rotação terrestre, através do experimento do pêndulo, construído pelo físico francês Jean Bernard Léon Foucault.

A força inercial de Coriolis é representada pela seguinte fórmula:

$F{\scriptstyle {\text{cr}}}=-2m({\vec {\omega }}\times {\vec {v}})$

Descrição da fórmula:

• $F{\scriptstyle {\text{cr}}}$ = Força de coriolis perpendicular ao eixo de rotação

• $m$ = massa da partícula

• ${\vec {v}}$= vetor velocidade

• ${\vec {\omega }}$ = velocidade angular

Força centrífuga

Aproveitando novamente o exemplo de um carro, porém agora em uma curva, se por um momento passarmos a considerar o momento da curva no ponto de vista de um observador externo parado (referencial inercial), pelo princípio da inercia o veiculo está destinado a sair pela tangente conservando sua velocidade. Para o respectivo observador as forças atuam garantindo a resultante força centrípeta.

Contudo, analisando o mesmo sistema, porém do ponto de vista do observador interno sabemos que ele está em um referencial não inercial, dado que, o observador possui aceleração em relação à estrada. Durante a curva este observador sente como se estivesse sendo arremessado para fora do carro , interpretando o fenômeno como uma força $F{\scriptstyle {\text{cf}}}$, chamada de Força Centrifuga. Resumidamente força centrifuga é a força exercida sob um corpo ou objeto em um movimento circular lançando-o para fora de um centro, ao contrario da força de Coriolis ela não depende da velocidade e sim da posição.

Uma pessoa parada em uma plataforma de um carrossel, sente uma força atirando-a para fora; é a força fictícia centrifuga, na qual se baseia em centrifugas, pois as forças que atuam nas partículas é proporcional à massa.

A experiência do balde de Newton é outro exemplo famoso feito por newton para provar que existe um sistema de referencia inercial e que também mostra ação da força centrifuga. O experimento consiste basicamente em um balde suspenso por uma corda que é enrolada em si mesma, enquanto o balde é mantido fixo. Em seguida quando se solta o balde e a corda começa a desenrolar, ele começa a girar rapidamente e depois a água começa a girar formando uma superfície concava , o que acontece devido a força centrifuga.

Expressão matemática da força inercial centrífuga para obter a descrição do movimento:

$F{\scriptstyle {\text{cf}}}={\vec {\omega }}\times ({\vec {\omega }}\times {\vec {r}})$

Descrição da fórmula:

• ${\vec {\omega }}$ = vetor velocidade angular

• ${\vec {r}}$= raio da distância do corpo ou objeto relacionado ao centro do referencial girante

Força fictícia e trabalho

As forças fictícias podem ser consideradas realizar trabalho, desde que  movam o objeto em uma trajetória de modo que altere sua energia do potencial para cinética. Por exemplo, considere uma pessoa em uma cadeira rotativa segurando um peso em sua mão estendida. Se eles puxarem a mão para dentro em direção ao seu corpo, na perspectiva do quadro de referência rotativo, eles trabalharam contra a força centrífuga. Quando o peso é solto, voa espontaneamente para fora em relação ao sistema de referência rotativo, porque a força centrífuga faz trabalho sob o objeto, convertendo sua energia potencial em cinética. Do ponto de vista inercial, é claro, o objeto é arremessado, porque de repente é possível  mover-se em linha reta. Isso ilustra que o trabalho feito, como a energia potencial total e a cinética de um objeto, podem ser diferentes em um sistema de referência  não inercial do que em um inercial.

Gravidade como uma força fictícia

A noção de "força fictícia" surge na teoria geral da relatividade de Einstein. Todas as forças fictícias são proporcionais à massa do objeto sobre o qual agem, o que também é verdadeiro para a gravidade. Isso levou Albert Einstein a se perguntar se a gravidade também era uma força fictícia. Ele constatou que um observador em queda livre dentro em uma caixa fechada não seria capaz de detectar a força da gravidade; Portanto, os sistemas de referência em queda livre são equivalentes a um sistema de referência inercial (o princípio da equivalência). Seguindo essa visão, Einstein pôde formular uma teoria da gravidade como força fictícia; Atribuindo a aparente aceleração da gravidade à curvatura do espaço-tempo. Essa ideia está subjacente à teoria da relatividade geral de Einstein. Veja Efeito de Eötvös.

Representação matemática das forças fictícias

Forças de inércia em um sistema de coordenadas em rotação

Figura 1: Coordenadas em um sistema de rotação

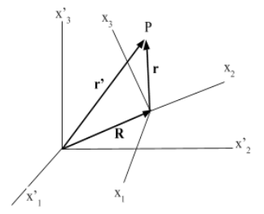
Para entendermos melhor o sistema de coordenadas ao lado (figura 1) vamos separa-los em dois tipos de eixos, "rotativos" e 'fixos", onde:

• $x'_{i}$ são coordenadas do sistema fixo;
• $x_{i}$ são coordenadas do sistema em rotação.

Agora temos:

$r'=R+r$

$r'$ é o raio de P no sistema fixo, e $r$ é o vetor do raio $P$ no sistema rotativo. O vetor $R$ se situa a partir da origem do sistema sistema rotativo no sistema fixo. Se imaginarmos o movimento instantâneo de um disco girando sobre um plano inclinado, este pode ser retratado como uma rotação em torno do ponto de contato entre o disco e plano. Em vista disso, o sistema de rotação $x_{i}$ realiza uma rotação infinitesimal $\delta \theta$, equivalendo a um deslocamento arbitrário infinitesimal, o movimento de $P$ pode ser pode ser reproduzido a partir da equação:

$(dr){\scriptstyle {\text{fixo}}}=d\theta \times r$

O termo $dr$ acima indica equivale a quantidade medida no sistema de coordenadas fixas. Para obtermos a taxa temporal de variação $r$, medida no sistema fixo, dividimos a equação anterior por $dt$, intervalo de tempo na qual ocorreu a respectiva rotação:

${\biggl (}{dr \over dt}{\biggr )}{\scriptstyle {\text{fixo}}}={d\theta \over dt}\times r$

com o fato da velocidade angular ser $\omega ={d\theta \over dt}$ possuímos: ${\biggl (}{dr \over dt}{\biggr )}{\scriptstyle {\text{fixo}}}=\omega \times r$

Se quisermos que P tenha velocidade $(\operatorname {d} \!r/\operatorname {d} \!t){\scriptstyle {\text{em rotação}}}$ em relação ao sistema rotativo essa velocidade deverá ser incluída em $\omega \times r$ para obter a taxa temporal de variação $r$ no sistema fixo: ${\biggl (}{dr \over dt}{\biggr )}{\scriptstyle {\text{fixo}}}={\biggl (}{dr \over dt}{\biggr )}{\scriptstyle {\text{em rotação }}}+\omega \times r$

Embora tenhamos obtido a equação acima com vetor $r$, o resultado pode ser aplicado a qualquer vetor $u$($t$). Podemos também aplicar o vetor $v$ ( velocidade da partícula), obtendo a aceleração $a$ da partícula:

${\biggl (}{dv \over dt}{\biggr )}{\scriptstyle {\text{fixo}}}=a={\biggl (}{dv \over dt}{\biggr )}{\scriptstyle {\text{em rotação }}}+\omega \times r$

Para calcular o primeiro termo derivamos em relação ao tempo , em $x_{i}$, os dois membros da equação com vetor em $r$:

${\biggl (}{dv \over dt}{\biggr )}{\scriptstyle {\text{em rotação}}}={\biggl (}{dv \over dt}{\biggr )}{\scriptstyle {\text{(a')}}}{\scriptstyle {\text{em rotação }}}+\omega \times {\biggl (}{dr \over dt}{\biggr )}{\scriptstyle {\text{(v')}}}{\scriptstyle {\text{em rotação}}}$

$a'$= aceleração em $x_{i}$

$v'$= velocidade em $x_{i}$

Substituindo a atual equação, na anterior ${\biggl (}{dv \over dt}{\biggr )}{\scriptstyle {\text{fixo}}}=a={\biggl (}{dv \over dt}{\biggr )}{\scriptstyle {\text{em rotação }}}+\omega \times r$, obtemos: $a=a'+\omega \times v'+\omega +v$

como $r=r'$ , finalmente : $a=a'+2\omega \times v+\omega \times (\omega \times r')$

Como a segunda lei de Newton $F=ma$ se transforma em $ma'=F+F{\scriptstyle {\text{fict}}}=ma$ em um sistema em rotação, obtemos, finalmente, a expressão geral das forças inerciais ou fictícias

$F{\scriptstyle {\text{fict}}}=-2m\omega \times v'-m\omega \times (\omega \times r)$

sendo que o ultimo termo é a expressão geral da força centrifuga e o primeiro a força de coriolis.

Ver também

• Dinâmica
• Força de Euler
• Força inercial centrífuga
• Força inercial de Coriolis
• Mecânica clássica
• Princípio de d'Alembert
• Referencial inercial
• Referencial não inercial
• Sistema de referência em rotação