Geometria não euclidiana

Um triângulo nas geometrias elíptica, hiperbólica e euclidiana.

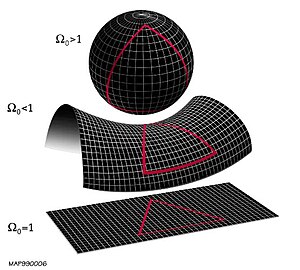
Na matemática, uma geometria não euclidiana é uma geometria baseada num sistema axiomático distinto da geometria euclidiana. Modificando o axioma das paralelas, que postula que por um ponto exterior a uma reta passa exatamente uma reta paralela à inicial, obtêm-se as geometrias elíptica e hiperbólica (geometria de Lobachevsky). Na geometria elíptica não há nenhuma reta paralela à inicial, enquanto que na geometria hiperbólica existe uma infinidade de rectas paralelas à inicial que passam no mesmo ponto. Na geometria elíptica a soma dos ângulos internos de um triangulo é maior que dois ângulos retos, enquanto na geometria hiperbólica esta soma é menor que dois ângulos retos. Na elíptica, temos que a circunferência de um círculo é menor do que PI vezes o seu diâmetro, enquanto na hiperbólica esta circunferência é maior que PI vezes o diâmetro.

O crédito pela descoberta das geometrias não euclidianas geralmente é atrelado às figuras dos matemáticos Carl Friedrich Gauss, e Bernhard Riemann.

Leitura adicional

• David E. Rowe. Euclidean geometry and physical space. The Mathematical Intelligencer / Volume 28, Number 2 (2006), 51-59. Issn: 0343-6993