Reflexão com deslizamento


Na geometria bidimensional, uma reflexão com deslizamento (ou reflexão transladada, ou translação refletida (ou transflecção) é uma operação de simetria que consiste em uma reflexão sobre uma linha e, em seguida, uma translação ao longo dessa linha, combinados em uma única operação. A etapa intermediária entre a reflexão e a translação pode parecer diferente da configuração inicial, portanto, os objetos com simetria de deslizamento são, em geral, não simétricos apenas sob reflexão. Na teoria dos grupos, o plano de deslizamento é classificado como um tipo de isometria oposta ao plano euclidiano.
Um único deslize é representado como grupo de frisos p11g. Uma reflexão com deslizamento pode ser vista como uma rotorreflexão limitante, onde a rotação se torna uma translação. Também pode ser dada uma notação Schoenflies como S 2∞, notação Coxeter como [∞ +, 2 + ] e notação orbifold como ∞ ×.
Descrição[editar | editar código-fonte]
A combinação de uma reflexão em uma linha e uma translação em uma direção perpendicular é uma reflexão em uma linha paralela. No entanto, uma reflexão com deslizamento não pode ser reduzida dessa forma. Portanto, o efeito de uma reflexão combinado com qualquer translação é uma reflexão deslizante, sendo um caso especial apenas uma reflexão. Esses são os dois tipos indiretos de isometrias em 2D .
Por exemplo, existe uma isometria que consiste na reflexão sobre o eixo x, seguida por uma translação de uma unidade paralela a ela. Em coordenadas, leva à seguinte fórmula:
- ( x, y ) → ( x + 1, - y ).
Ele corrige um sistema de linhas paralelas.
O grupo de isometria gerado apenas por uma reflexão com deslizamento é um grupo cíclico infinito.[1]
Combinando duas reflexões de deslizamento iguais, dá uma translação pura com um vetor de translação que é duas vezes maior do que o vetor de reflexão com deslizamento, portanto, os poderes pares da reflexão com deslizamento formam um grupo de translação.
No caso de simetria de reflexâo de deslizamento, o grupo de simetria de um objeto contém um reflexo de deslizamento e, portanto, o grupo gerado por ele. Se isso for tudo o que ele contém, este tipo é o grupo de frisos p11g.
Exemplo padrão com este grupo de simetria:
Grupo Frieze nº. 6 (reflexos de deslizamento, translações e rotações) é gerado por uma reflexão com deslizamento e uma rotação em torno de um ponto na linha de reflexão. É isomórfico a um produto semidireto de Z e C 2 .
Exemplo padrão com este grupo de simetria:
Um exemplo típico de reflexão com deslizamento na vida cotidiana seria o rastro de pegadas deixadas na areia por uma pessoa caminhando na praia.
Para qualquer grupo de simetria contendo alguma simetria de reflexão com deslizamento, o vetor de translação de qualquer reflexão com deslizamento é a metade de um elemento do grupo de translação. Se o vetor de translação de uma reflexão com deslizamento é ele próprio um elemento do grupo de translação, então a simetria de reflexão com deslizamento correspondente se reduz a uma combinação de simetria de reflexão e simetria de translação .
A simetria da reflexão com deslizamento em relação a duas linhas paralelas com a mesma translação implica que também há simetria de translação na direção perpendicular a essas linhas, com uma distância de translação que é duas vezes a distância entre as linhas de reflexão com deslizamento. Isso corresponde ao grupo de papel de parede pg; com simetria adicional ocorre também em pmg, pgg e p4g.
Se também houver linhas de reflexão verdadeiras na mesma direção, então elas serão espaçadas igualmente entre as linhas de reflexão com deslizamento. Uma linha de reflexão com deslizamento paralela a uma linha de reflexão verdadeira já implica esta situação. Isso corresponde ao grupo de papel de parede cm. A simetria translacional é dada por vetores de translação oblíquos de um ponto em uma linha de reflexão verdadeira para dois pontos na próxima, apoiando um losango com a linha de reflexão verdadeira como uma das diagonais. Com simetria adicional, ocorre também em cmm, p3m1, p31m, p4m e p6m.
Em 3D, a reflexão com deslizamento é chamada de plano de deslizamento . É uma reflexão em um plano combinada com uma translação paralela ao plano.
Grupos de papel de parede[editar | editar código-fonte]
No plano euclidiano, 3 de 17 grupos de papel de parede requerem geradores de reflexão com deslizamento. p2gg tem reflexos de deslizamento ortogonais e rotações de 2 vezes. cm possui espelhos paralelos e deslizamentos, e pg possui deslizamentos paralelos. (Reflexos de deslizamento são mostrados abaixo como linhas tracejadas)
| Nome cristalográfico | pgg | cm | pg |
|---|---|---|---|
| Nome de Conway | 22 × | * × | × × |
| Diagrama | 
|

|
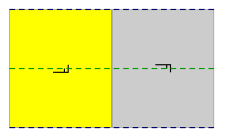
|
| Exemplo | 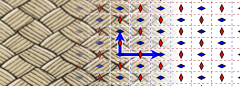
|

|

|
Deslize a reflexão na natureza e nos jogos[editar | editar código-fonte]
A simetria de deslizamento pode ser observada na natureza entre alguns fósseis da biota de Ediacara ; os machaeridianos ; e certos vermes paleoescolecídeos .[2] Também pode ser visto em muitos grupos existentes de canetas marinhas .[3]
A reflexão com deslizamento é comum no Jogo da Vida de Conway ao produzir Gun (autômato celular) .
Referências
- ↑ Martin, George E. (1982), Transformation Geometry: An Introduction to Symmetry, ISBN 9780387906362, Undergraduate Texts in Mathematics, Springer, p. 64
- ↑ Waggoner, B. M. (1996). «Phylogenetic Hypotheses of the Relationships of Arthropods to Precambrian and Cambrian Problematic Fossil Taxa». Systematic Biology. 45: 190–222. JSTOR 2413615. doi:10.2307/2413615
- ↑ Zubi, Teresa (2 de janeiro de 2016). «Octocorals (Stoloniferans, soft corals, sea fans, gorgonians, sea pens) - Starfish Photos - Achtstrahlige Korallen (Röhrenkorallen, Weichkorallen, Hornkoralllen, Seefedern, Fächerkorallen)». starfish.ch. Consultado em 8 de setembro de 2016
