Teoria de resposta ao item
A Teoria da Resposta ao Item[nota 1], muitas vezes abreviada apenas por TRI, é um ramo da Teoria da Medida direcionado predominantemente ao estudo de questionários e outras listas de itens, com ampla aplicação em diferentes áreas, tais como Econometria, Psicometria, Publicidade, ranking esportivo, Sociologia, Pedagogia etc. No campo da Psicometria, a TRI distingue-se da Teoria Clássica dos Testes (TCT) por dar uma abordagem em que se investiga individualmente as propriedades de cada item, ao passo que na Teoria Clássica dos Testes se investiga as propriedades do conjunto de itens que constituem o teste. Uma das vantagens da TRI em comparação à TCT é que a primeira possibilita construir vários exames constituídos por alguns itens exclusivos e alguns itens compartilhados, e assegurar que o nível de dificuldade de todos os exames seja aproximadamente igual. Ela é atualmente utilizada em testes como o TOEFL e o ENEM.
Aplicação
[editar | editar código-fonte]A aplicação mais frequente da Teoria da Resposta ao Item são as avaliações de habilidades e conhecimentos em Testes de Múltipla escolha. A Teoria da Resposta ao Item, contudo, pode abranger também testes dissertativos além de poder abarcar várias outras áreas. O caso mais famoso de aplicação da Teoria da Resposta ao Item é no ranqueamento de atletas, especialmente no Xadrez. O Sistema Elo é baseado no modelo mais simples de TRI, o modelo de Rash, e vem sendo amplamente utilizado pela FIDE desde 1971. Uma das importantes vantagens de se usar TRI em vez de outros métodos para ranqueamento, é que, se alguns cuidados forem tomados no processo de normatização, torna-se possível gerar escores em escala de proporção. Nos casos de esportes, estes escores permitem predições probabilísticas muito mais acuradas sobre o desempenho dos atletas do que qualquer outro método.[carece de fontes]
A Teoria da Resposta ao Item é utilizada em avaliações de vários países, onde os programas de avaliação mais conhecidos são o NAEP[2] nos Estados Unidos da América, o ETS[3] nos Estados Unidos da América, o GMAT[4] nos Estados Unidos da América, o CITO[5] na Holanda e vários outros. No Brasil o principal programa de avaliação que utiliza a Teoria da Resposta ao Item é o SAEB, que desde sua criação em 1995 a utiliza para estimar as habilidades e conhecimentos dos alunos do Ensino Fundamental e Médio das escolas públicas brasileiras através de amostragem do universo desses alunos. A partir de 2005 este programa busca avaliar de forma censitária toda a rede pública do país. O novo Enem, reformulado a partir de 2009, também faz uso da TRI[6], de forma a garantir a comparabilidade das notas entre diferentes edições. Esta foi a aplicação de maior impacto na divulgação da Teoria da Resposta ao Item.
História
[editar | editar código-fonte]A Teoria da Resposta ao Item surgiu a partir de discussões teóricas sobre a viabilidade de se comparar as habilidades e os conhecimentos de examinandos submetidos a provas diferentes. A Teoria Clássica dos Testes, principal teoria estatística para medida dessas características na época, via-se diante de enormes dificuldades para comparar as habilidades e os conhecimentos de examinandos submetidos a provas diferentes. Nesse sentido, em 1950, Gulliksen, H definiu, no âmbito da Teoria Clássica dos Testes que duas provas podem ser consideradas formas paralelas quando, após a conversão para a mesma escala, suas médias, desvios padrão de acertos bem como demais correlações do número de acertos com todo e qualquer outro critério fossem iguais. Em 1971, ainda no âmbito da Teoria Clássica dos Testes, Angoff, W delimita a equivalência de provas ao apresentar as seguintes exigências:
- As provas devem medir predominantemente a mesma característica ou habilidade;
- A equivalência estabelecida deve ser tão independente quanto possível dos dados em particular utilizados para estabelecer esse princípio e deve ser aplicável em todas as situações parecidas;
- Os escores de duas provas, uma vez estabelecida sua equivalência, devem ser substituíveis entre si, e;
- A equivalência deve ser simétrica, ou seja, não deve fazer distinção entre a prova particular escolhida como base de referência.
As duas últimas propriedades citadas acima também podem estar presentes quando se normatiza um teste por meio da TCT, mas exige que um maior número de condições sejam atendidas no que diz respeito à equivalência entre os grupos de pessoas examinados com os dois (ou mais) testes. Em TRI há necessidade de atender a um número menor de condições para se alcançar resultados de mesma qualidade.
Ainda no âmbito da Teoria Clássica dos Testes, em 1977, Lord, F M estende as considerações levantadas por Angoff. A noção de escores substituíveis ganha nova dimensão com a introdução do conceito de equidade: Os escores transformados y* e observados x podem ser considerados "equivalentes" quando houver indiferença se um examinando responder a prova X ou Y. De acordo com esse princípio:
- Torna-se inviável a tentativa de se estabelecer a equivalência entre provas que medem diferentes características ou habilidades (consistente com a primeira restrição de Angoff);
- A equivalência de escores com margens de erro desiguais não pode ser estabelecida (consistente com os escores substituíveis de Angoff);
- Não se pode estabelecer a equivalência de provas que refletem diferentes níveis de dificuldades.
Segundo Lord, se as provas X e Y têm dificuldades diferentes, a relação entre seus escores verdadeiros é necessariamente não linear devido aos efeitos de piso e de teto. Se duas provas têm uma relação não linear é implausível que elas sejam igualmente fidedignas em todos os grupos de examinandos. Isso leva à conclusão incômoda de que, a rigor, não se pode tornar equivalentes os escores observados em provas de dificuldades diferentes. Todo esse panorama levou Lord a defender as vantagens teóricas dos modelos da teoria da resposta ao item em procedimentos que estabelecem a equivalência dos resultados de provas.
Fundamentos
[editar | editar código-fonte]A Teoria da Resposta ao Item trata o problema da estimação da habilidade e conhecimento de um examinando de forma essencialmente diferente: o enfoque das análises desvincula-se das provas (Teoria Clássica dos Testes) e concentra-se nos Itens; se na Teoria Clássica dos Testes as estatísticas dos itens dependem da população dos examinandos e da prova à qual os itens pertencem, na Teoria da Resposta ao Item cria-se o conceito de que os parâmetros dos itens, obtidos no processo estatístico de "calibração" dos parâmetros de dificuldade, discriminação e acerto casual dos itens (Valle, R) são características próprias dos mesmos. Costuma-se considerar que a característica de medição dos Itens, representados por seus parâmetros, são invariantes no tempo com algumas ressalvas, por exemplo: um item que aborde o conhecimento sobre eclipses solares e lunares estará sujeito a variações de suas características de medição conforme o modismo, sobretudo quando um eclipse ocorre; em casos como esse, a invariância dos parâmetros do item no tempo não deve ser considerada como verdadeira.
Consideradas as ponderações anteriores, uma característica fundamental para a viabilidade de comparação da habilidade e conhecimento de examinandos submetidos a provas diferentes é que a Teoria da Resposta ao Item modela a probabilidade de acerto a um item, também conhecida como Curva Característica do Item, através de uma função não linear do conhecimento dos examinandos. Essa característica da modelagem da Teoria da Resposta ao Item é de grande importância pois, desse modo, é possível comparar o conhecimento dos examinandos submetidos a provas diferentes sendo necessário apenas que as provas meçam as mesmas características; essa propriedade é essencialmente útil para sistemas de avaliações onde é possível submeter uma grande quantidade de tópicos de uma matéria em sala de aula (útil para se ter um painel geral sobre o ensino de vários tópicos) com os alunos respondendo apenas um conjunto pequeno dos itens utilizados na avaliação (útil para não tornar as provas excessivamente extensas). Uma boa referência sobre o assunto é Andrade, D.F, Tavares, H.R. & Valle, R.C. (2000).
Modelagem Estatística
[editar | editar código-fonte]A modelagem mais moderna para a Teoria da Resposta ao Item utiliza a Estatística Bayesiana. Nessa modelagem, a probabilidade de acerto de um item é condicionada à habilidade e conhecimento do examinando. A curva que modela a probabilidade de acerto de um item é uma função crescente na ordenada da habilidade e conhecimento; o gráfico que tem a probabilidade condicional de acerto de um item na ordenada e a habilidade e conhecimento na abscissa é conhecido como Curva Característica do Item.
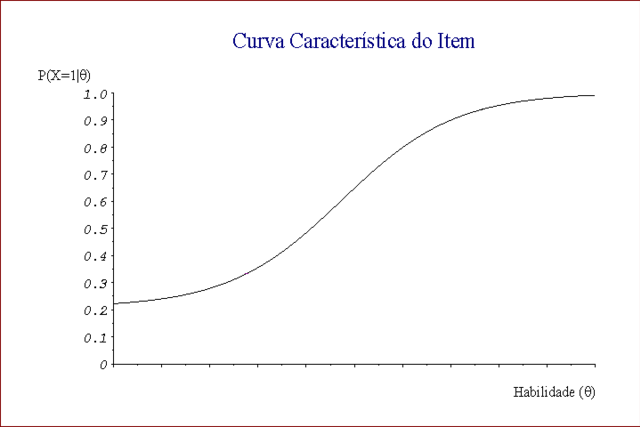
Na abordagem bayesiana da Teoria da Resposta ao Item costuma-se representar a habilidade e conhecimento por uma variável aleatória simbolizada pela letra grega ; a variável aleatória que representa o acerto ou erro de um item ´s simbolizada pela letra ; o resultado (acerto ou erro) de um item respondido é representado por , onde normalmente representa o acerto do item e representa o erro. O gráfico da Curva Característica do Item acima é portanto um gráfico que associa a probabilidade de acerto em função de . Adicionalmente costuma-se utilizar o índice para indicar um examinando específico ( representa a habilidade e conhecimento do examinando ) e o índice para indicar um item específico ( representa os possíveis resultados do item e representa a resposta do examinando ao item ).
Existe uma gama extensa de modelos da Teoria da Resposta ao Item: os modelos mais complexos podem considerar uma multidimensionalidade da habilidade e conhecimento onde a variável teta que a representa é um vetor multidimensional como também considerar a abordagem de créditos parciais para acomodar itens com estágios hierárquicos de desenvolvimento, por exemplo: primeiro estágio se nada está correto na resolução do item (). segundo estágio se o item foi corretamente esquematizou o problema corretamente (); terceiro estágio se o desenvolvimento do raciocínio está correto () e quarto estágio se o item foi respondido corretamente na íntegra (). O modelo de créditos parciais, embora pouco utilizado, é adequado para questões discursivas.
O modelo mais simples e usual da Teoria da Resposta ao Item considera itens dicotômicos (onde os possíveis resultados são acerto ou erro) e uma função logística para modelar a Curva Característica do Item:
Na modelagem bayesiana da Teoria da Resposta ao Item, conforme citado no início, diz-se que as respostas onde é o número de itens respondidos pelo examinando estão correlacionadas através da habilidade e conhecimento do examinando. Se fosse conhecido, as respostas seriam independentes estatisticamente. Essa abordagem costuma suscitar algumas confusões pois para o cálculo da verossimilhança utilizaremos o fato de que , , ..., são independentes estatisticamente, ao passo que , , ..., são estatisticamente dependentes. Essa propriedade é conhecida como independência condicional e pode ser estudada em mais detalhes em artigo de De Finetti, B; por ora consideremos que se soubéssemos o verdadeiro valor da habilidade e conhecimento de um examinando as suas respostas a um conjunto de itens seriam estatisticamente independentes pois já saberíamos sua habilidade. Dessa forma, submetê-lo a um conjunto de itens seria inútil: os acertos e erros aos itens seriam meramente aleatórios. Para que a Teoria da Resposta ao Item seja aplicável é necessário pressupor que a habilidade e conhecimento de um examinando seja conhecido através de uma incerteza, representada por uma distribuição de probabilidade, e que os acertos e erros de um examinando numa prova revelem informações sobre seus conhecimentos e habilidades.
Considerando a propriedade da independência condicional dos acertos e erros dos itens respondidos por um examinando, a verossimilhança gerada pelas respostas de um examinando é dada por:
Após o examinando responder um conjunto de itens a estimativa da habilidade e conhecimento pode ser facilmente calculada através do Operador de Bayes:
Onde é a distribuição de probabilidade a priori para a habilidade e conhecimento do examinando , : é a verossimilhança gerada pelas respostas aos itens e é a distribuição de probabilidade a posteriori para o mesmo examinando ao responder os itens .
Ver também
[editar | editar código-fonte]Referências
- ↑ http://portal.mec.gov.br/ultimas-noticias/389-ensino-medio-2092297298/17319-teoria-de-resposta-ao-item-avalia-habilidade-e-minimiza-o-chute
- ↑ NAEP - National Assessment of Educational Progress
- ↑ ETS - Educational Testing Service
- ↑ GMAT - Graduate Management Admission Test
- ↑ CITO - Institute for Educational Measurement
- ↑ TRI: a teoria por trás do novo Enem
Bibliografia
[editar | editar código-fonte]- Andrade, D. F., Tavares, H. R., Valle, R. C.(2000). Teoria da Resposta ao Item. Conceitos e Aplicações. Associação Brasileira de Estatística: São Paulo.
- Andrade, D., Valle, R. (1998). Introdução à Teoria da Resposta ao Item. Estudos em Avaliação Educacional. São Paulo: Fundação Carlos Chagas, 18, 13-32.
- Angoff, W. (1971). Scales, Norms, and Equivalent Scores. In R. L. Thorndike (Ed.), Educational Measurement (2nd. ed.), Washington, D.C.: American Council on Education.
- Gulliksen, H (1950). Theory of Mental Tests. New York: Wiley.
- De Finetti, B. (1931). Funzione caratteristica di un fenomeno aleatorio. Atti della R. Accademia Nazionale dei Lincei, Serie 6. Memorie, Classe di Scienze Fisiche, Mathematice e Naturale, 4:251–299.
- Fletcher, P (1995). Procedimentos para Estabelecer a Equivalência de Provas com Modelos da Resposta ao Item. Ensaio. Rio de Janeiro. v. 3, n. 6, p. 41-54.
- Lord, F M.. (1977). Pratical Applications of Item Response Theory to Pratical Testing Problems. Hillsdale, New Jersey: Lawrence Erlbaum.
- Lord, F M., & Novick, M R, (1968). Statistical Theories of Mental Test Scores. Reading Mass: Addison-Wesley.
- Klein, R. (2003). Utilização da Resposta ao Item no Sistema Nacional de Avaliação da Educação Básica (SAEB). Ensaio: Avaliação e Políticas Públicas em Educação. Rio de Janeiro, 11, 40, 283-96.
- Mislevy, J., Bock, D (1990). BILOG 3: Item Analysis and Test Scoring with Binary Logistic Models. Chicago: Scientific Software Inc.
- Tavares, H. R. (2001). Teoria da Resposta ao Item para Dados Longitudinais. Tese de Doutorado. Universidade de São Paulo.
- Valle, R. (2000). Teoria da Resposta ao Item. Estudos em Avaliação Educacional. São Paulo: Fundação Carlos Chagas, 21, 7-91.
- Valle, R. (2001). Construção e Interpretação de Escalas de Conhecimento: um Estudo de Caso. Estudos em Avaliação Educacional. São Paulo: Fundação Carlos Chagas, 23, 71-92.
































