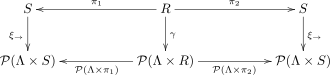Bissimulação: diferenças entre revisões
m Foram revertidas as edições de Bresende para a última revisão de Yanguas, de 21:33, fevereiro 25, 2015 (UTC) |
Adição de fontes/referências e correção de erros |
||
| Linha 1: | Linha 1: | ||
| ⚫ | Na [[ciência da computação teórica | teoria da computação]] uma '''bissimulação''' é uma [[relação binária]] entre sistemas de transição de estados, ou também chamados apenas de sistemas de transição (sistemas constituintes de estados e transições<ref>BAIER, Christel;KATOEN, Joost-Pieter. Principles of model checking. [S.l.]: The MIT Press. 20 p.</ref>), associando sistemas que se comportam da mesma maneira no sentido de que um sistema simula o outro e vice-versa. |
||
{{mais notas|data=fevereiro de 2015}} |
|||
| ⚫ | |||
Intuitivamente dois sistemas são '''bissimilares''' se eles combinam seus movimentos entre si. Neste sentido, cada um dos sistemas não pode ser distinto um do outro por um observador. |
Intuitivamente dois sistemas são '''bissimilares''' se eles combinam seus movimentos entre si. Neste sentido, cada um dos sistemas não pode ser distinto um do outro por um observador. |
||
| Linha 41: | Linha 40: | ||
A relação de bissimilaridade <math> \, \sim \, </math> é uma [[relação de equivalência]]. Além disso, ela é a mais larga relação de bissimulação sobre um dado sistema de transição. |
A relação de bissimilaridade <math> \, \sim \, </math> é uma [[relação de equivalência]]. Além disso, ela é a mais larga relação de bissimulação sobre um dado sistema de transição. |
||
Note que não é sempre o caso que se <math>p</math> simula <math>q</math> e <math>q</math> simula <math>p</math> que eles são bissimilares. Para <math>p</math> e <math>q</math> serem bissimilares, a simulação entre <math>p</math> e <math>q</math> deve ser a inversa da simulação entre <math>p</math> e <math>q</math>. Contraexemplo (em Sistemas de Comunicação de Cálculos, descrevendo uma máquina de café): <math>M=p.\overline{c}.M+p.\overline{t}.M+p.(\overline{c}.M+\overline{t}.M)</math> e <math>M'=p.(\overline{c}.M'+\overline{t}.M')</math> simulam entre |
Note que não é sempre o caso que se <math>p</math> simula <math>q</math> e <math>q</math> simula <math>p</math> que eles são bissimilares. Para <math>p</math> e <math>q</math> serem bissimilares, a simulação entre <math>p</math> e <math>q</math> deve ser a inversa da simulação entre <math>p</math> e <math>q</math>. Contraexemplo (em Sistemas de Comunicação de Cálculos<ref>MILNER, Robin. Communication and Concurrency. [S.l.]: Prentice Hall, 1989.</ref>, descrevendo uma máquina de café): <math>M=p.\overline{c}.M+p.\overline{t}.M+p.(\overline{c}.M+\overline{t}.M)</math> e <math>M'=p.(\overline{c}.M'+\overline{t}.M')</math> simulam entre |
||
si mas não são bissimilares. |
si mas não são bissimilares. |
||
| Linha 47: | Linha 46: | ||
=== Definição relacional === |
=== Definição relacional === |
||
Bissimulação pode ser definida em termos de composições de relações como segue. |
Bissimulação pode ser definida em termos de composições de relações<ref>HIRSCH, Edward A.; KARHUMÄKI, Juhani; LEPISTÖ, Arto (2012). "Computer Science - Theory and Applications" in 7th International Computer Science Symposium in Russia, CSR 2012 Nizhny Novgorod, Russia. PRILUTSKII, Michail Computer Science - Theory and Applications: 191, Springer Science.</ref> como segue. |
||
Dado um sistema de transição rotulado <math>(S, \Lambda, \rightarrow)</math>, uma relação de ''bissimulação'' é uma [[relação binária]] de <math>R</math> sobre <math>S</math> (isto é, <math>R</math> ⊆ <math>S</math> × <math>S</math>) tal que <math>\forall\alpha\in\Lambda</math> |
Dado um sistema de transição rotulado <math>(S, \Lambda, \rightarrow)</math>, uma relação de ''bissimulação'' é uma [[relação binária]] de <math>R</math> sobre <math>S</math> (isto é, <math>R</math> ⊆ <math>S</math> × <math>S</math>) tal que <math>\forall\alpha\in\Lambda</math> |
||
| Linha 58: | Linha 57: | ||
=== Definição ponto fixo === |
=== Definição ponto fixo === |
||
Bissimilaridade também pode ser definida |
Bissimilaridade também pode ser definida da maneira da [[teoria da ordem]], em termos da teoria do ponto fixo<ref>PARK, David (1981). "Concurrency and Automata on Infinite Sequences" in Proceedings of the 5th GI-Conference, Karlsruhe. Deussen, Peter Theoretical Computer Science 104: 167–183</ref>, mais precisamente como o maior ponto fixo de uma certa função definida abaixo. |
||
Dado um sistema de transição rotulado (<math>S</math>, Λ, →), defina <math>F:\mathcal{P}(S \times S) \to \mathcal{P}(S \times S)</math> para ser uma função de relações binárias sobre <math>S</math> a relações binárias sobre <math>S</math>, como segue: |
Dado um sistema de transição rotulado (<math>S</math>, Λ, →), defina <math>F:\mathcal{P}(S \times S) \to \mathcal{P}(S \times S)</math> para ser uma função de relações binárias sobre <math>S</math> a relações binárias sobre <math>S</math>, como segue: |
||
| Linha 81: | Linha 80: | ||
=== Definição da teoria dos jogos === |
=== Definição da teoria dos jogos === |
||
Bissimulação também pode ser pensada em termos de um jogo entre dois jogadores, atacante e defensor. |
Bissimulação também pode ser pensada em termos de um jogo<ref>SOBOCINSKI, Pawel. Bisimulation, Games & Hennessy Milner logic Lecture 1 of Modelli Matematici dei Processi Concorrenti 15-18 pp.. Visitado em 05/03/2015.</ref> entre dois jogadores, atacante e defensor. |
||
O "Atacante" vai primeiro e pode escolher qualquer transição válida, <math>\alpha</math>, de <math>(p,q)</math>. Isto é.: |
O "Atacante" vai primeiro e pode escolher qualquer transição válida, <math>\alpha</math>, de <math>(p,q)</math>. Isto é.: |
||
| Linha 115: | Linha 114: | ||
=== Definição co-algébrica === |
=== Definição co-algébrica === |
||
Uma bissimulação do sistema de transição de estados é um caso especial de bissimulação co-algébrica para o tipo de |
Uma bissimulação do sistema de transição de estados é um caso especial de bissimulação co-algébrica<ref>VAN BREUGEL, Franck; KASHEFI, Elham; PALAMIDESSI, Catuscia. "A Tribute to Prakash Panangaden" in Essays Dedicated to Prakash Panangaden on the Occasion of His 60th Birthday. RUTTEN, Jan Horizons of the Mind: 82, Springer Science.</ref> para o tipo de funtor covariante do conjunto das partes. Note que todo o sistema de transições de estados <math>(S, \Lambda, \rightarrow)</math> é bijetivamente uma função <math>\xi_{\rightarrow} </math> do <math>S</math> para o conjunto das partes de <math>S</math> indexado por <math>\Lambda</math> escrito como <math>\mathcal{P}(\Lambda \times S)</math>, definido por |
||
::<math> p \mapsto \{ (\alpha, q) \in S : p \overset{\alpha}{\rightarrow} q \}.</math> |
::<math> p \mapsto \{ (\alpha, q) \in S : p \overset{\alpha}{\rightarrow} q \}.</math> |
||
| Linha 122: | Linha 121: | ||
onde <math>P</math> é um subconjunto de <math>\Lambda \times S \times S</math>. Similarmente para <math>\mathcal{P}(\Lambda \times \pi_2)</math>. |
onde <math>P</math> é um subconjunto de <math>\Lambda \times S \times S</math>. Similarmente para <math>\mathcal{P}(\Lambda \times \pi_2)</math>. |
||
Usando as notações acima, a relação <math>R \subseteq S \times S </math> é uma '''bissimulação''' num sistema de transição <math>(S, \Lambda, \rightarrow)</math> se e somente se existe um sistema de transição <math>\gamma \colon R \to \mathcal{P}(\Lambda \times R)</math> na relação R tal que o diagrama |
Usando as notações acima, a relação <math>R \subseteq S \times S </math> é uma '''bissimulação''' num sistema de transição <math>(S, \Lambda, \rightarrow)</math> se e somente se existe um sistema de transição <math>\gamma \colon R \to \mathcal{P}(\Lambda \times R)</math> na relação <math>R</math> tal que o diagrama |
||
[[image:Coalgebraic bisimulation.svg|frameless|upright=1.5]] |
[[image:Coalgebraic bisimulation.svg|frameless|upright=1.5]] |
||
| Linha 131: | Linha 130: | ||
== Variantes de bissimulação == |
== Variantes de bissimulação == |
||
Em contextos especiais a noção de bissimulação as vezes é refinada pela adição de requisitos adicionais e restrições. Por exemplo se o sistema de transição de estado inclui a noção de ação ''silenciosa'' (ou ''interna''), geralmente denotada com <math>\tau</math>, isto é ações que não são visíveis por observadores externos, então bissimulação pode ser descontraída para ser uma ''bissimulação fraca'', a qual se dois estados <math>p</math> e <math>q</math> são bissimilares e existe algum número de ações internas começando por <math>p</math> a outro estado <math>p'</math> então deve existir o estado <math>q'</math> tal que existe algum número (possivelmente zero) de ações internas começando por <math>q</math> a <math>q'</math>. |
Em contextos especiais a noção de bissimulação as vezes é refinada pela adição de requisitos adicionais e restrições. Por exemplo se o sistema de transição de estado inclui a noção de ação ''silenciosa'' (ou ''interna''), geralmente denotada com <math>\tau</math>, isto é ações que não são visíveis por observadores externos, então a bissimulação pode ser descontraída para ser uma ''bissimulação fraca'', a qual se dois estados <math>p</math> e <math>q</math> são bissimilares e existe algum número de ações internas começando por <math>p</math> a outro estado <math>p'</math> então deve existir o estado <math>q'</math> tal que existe algum número (possivelmente zero) de ações internas começando por <math>q</math> a <math>q'</math>. |
||
Tipicamente, se o sistema de transição de estado dá a [[semântica operacional]] de uma [[linguagem de programação]], então a definição precisa de bissimulação será específica às restrições da linguagem de programação. Portanto, no geral, pode existir mais de um tipo de bissimulação, |
Tipicamente, se o sistema de transição de estado dá a [[semântica operacional]] de uma [[linguagem de programação]], então a definição precisa de bissimulação será específica às restrições da linguagem de programação. Portanto, no geral, pode existir mais de um tipo de bissimulação, a relação depende do contexto. |
||
== Bissimulação e lógica modal == |
== Bissimulação e lógica modal == |
||
Desde que os [[semânticas de Kripke|modelos de Kripke]] são um caso especial de sistema de transição de estado (rotulado), bissimulação também é um tópico de [[lógica modal]]. Na verdade, lógica modal é o fragmento de [[lógica de primeira ordem]] invariante sob bissimulação ([[Johan van Benthem|teorema de Van Benthem]]). |
Desde que os [[semânticas de Kripke|modelos de Kripke]]<ref>DRAGOMIR, Alexandru. "Minimal Models and Bisimulation in Modal Logic". Acessado em 05/03/2015.</ref> são um caso especial de sistema de transição de estado (rotulado), bissimulação também é um tópico de [[lógica modal]]. Na verdade, lógica modal é o fragmento de [[lógica de primeira ordem]] invariante sob bissimulação ([[Johan van Benthem|teorema de Van Benthem]]). |
||
== Veja também == |
== Veja também == |
||
* [[Semântica operacional]] |
* [[Semântica operacional]] |
||
* Sistemas de transição de estados |
|||
* Simulação pre-órdem |
|||
* Relação de congruência |
|||
* Bissimulação probabilística |
|||
== Ferramentas de software == |
== Ferramentas de software == |
||
| Linha 154: | Linha 149: | ||
# {{Cite conference |
# {{Cite conference |
||
| first = David |
| first = David |
||
| last = |
| last = PARK |
||
| year = 1981 |
| year = 1981 |
||
| title = Concurrency and Automata on Infinite Sequences |
| title = Concurrency and Automata on Infinite Sequences |
||
| Linha 168: | Linha 163: | ||
}} |
}} |
||
# {{Cite book |
# {{Cite book |
||
| last = |
| last = MILNER |
||
| first = Robin |
| first = Robin |
||
| title = Communication and Concurrency |
| title = Communication and Concurrency |
||
| Linha 175: | Linha 170: | ||
| isbn = 0-13-114984-9 |
| isbn = 0-13-114984-9 |
||
}} |
}} |
||
# {{Cite book |
|||
| last = BAIER, Christel; KATOEN, Joost-Pieter |
|||
| title = Principles of model checking |
|||
| pages = 20 |
|||
| publisher = The MIT Press |
|||
| isbn = 978-0-262-02649-9 |
|||
}} |
|||
# {{Cite conference |
|||
| last = HIRSCH, Edward A.; KARHUMÄKI, Juhani; LEPISTÖ, Arto |
|||
| year = 2012 |
|||
| title = Computer Science - Theory and Applications |
|||
| conference = 7th International Computer Science Symposium in Russia, CSR 2012 Nizhny Novgorod, Russia |
|||
| booktitle = Computer Science - Theory and Applications |
|||
| editor = PRILUTSKII, Michail |
|||
| pages = 191 |
|||
| publisher = Springer Science |
|||
| isbn = 978-3-642-30641-9 |
|||
}} |
|||
#{{Citar web |
|||
| url = http://web.cs.wpi.edu/~guttman/cs521_website/sobocinski_bisimulation-nup.pdf |
|||
| título = Bisimulation, Games & Hennessy Milner logic |
|||
| acessadoem = 05/03/2015 |
|||
| autor = SOBOCINSKI, Pawel |
|||
| obra = Lecture 1 of Modelli Matematici dei Processi Concorrenti |
|||
| páginas = 15-18 |
|||
}} |
|||
#{{Cite conference |
|||
| last = VAN BREUGEL, Franck; KASHEFI, Elham; PALAMIDESSI, Catuscia |
|||
| year = |
|||
| title = A Tribute to Prakash Panangaden |
|||
| conference = Essays Dedicated to Prakash Panangaden on the Occasion of His 60th Birthday |
|||
| booktitle = Horizons of the Mind |
|||
| editor = RUTTEN, Jan |
|||
| pages = 82 |
|||
| publisher = Springer Science |
|||
| isbn = 978-3-319-06879-4 |
|||
}} |
|||
#{{Referência a artigo |
|||
| autor = DRAGOMIR, Alexandru |
|||
| título = Minimal Models and Bisimulation in Modal Logic |
|||
| url = http://www.academia.edu/690794/Minimal_Models_and_Bisimulation_in_Modal_Logic |
|||
| acessadoem = 05/03/2015 |
|||
}} |
|||
== Leitura complementar == |
== Leitura complementar == |
||
* Davide Sangiorgi. (2011). Introduction to Bisimulation and Coinduction. Cambridge University Press. ISBN 9781107003637 |
* Davide Sangiorgi. (2011). Introduction to Bisimulation and Coinduction. Cambridge University Press. ISBN 9781107003637 |
||
Revisão das 04h36min de 6 de março de 2015
Na teoria da computação uma bissimulação é uma relação binária entre sistemas de transição de estados, ou também chamados apenas de sistemas de transição (sistemas constituintes de estados e transições[1]), associando sistemas que se comportam da mesma maneira no sentido de que um sistema simula o outro e vice-versa.
Intuitivamente dois sistemas são bissimilares se eles combinam seus movimentos entre si. Neste sentido, cada um dos sistemas não pode ser distinto um do outro por um observador.
Definição formal
Dado um sistema de transição rotulado (, Λ, →); uma relação de bissimulação é uma relação binária sobre (isto é, ⊆ × ) tal que ambos −1 e são simulações.
Equivalentemente é uma bissimulação se para cada par de elementos em com em , para todo α em Λ:
para todo em ,
- implica que existe um em tal que
- e ;
e, simetricamente, para todo em
- implica que existe um em tal que
- e .
Dados dois estados e em , é bissimilar a , escrito , se existe uma bissimulação tal que está em .
A relação de bissimilaridade é uma relação de equivalência. Além disso, ela é a mais larga relação de bissimulação sobre um dado sistema de transição.
Note que não é sempre o caso que se simula e simula que eles são bissimilares. Para e serem bissimilares, a simulação entre e deve ser a inversa da simulação entre e . Contraexemplo (em Sistemas de Comunicação de Cálculos[2], descrevendo uma máquina de café): e simulam entre si mas não são bissimilares.
Definições alternativas
Definição relacional
Bissimulação pode ser definida em termos de composições de relações[3] como segue.
Dado um sistema de transição rotulado , uma relação de bissimulação é uma relação binária de sobre (isto é, ⊆ × ) tal que
- e
Partindo da monotonicidade e continuidade da relação de composição, ela segue imediatamente que o conjunto de bissimulações é fechado sobre uniões (junta-se à ordem parcial das relações), e um simples cálculo algébrico mostra que a relação de bissimilaridade - a junção de todas as bissimulações - é uma relação de equivalência. Esta definição, e o tratamento associado a bissimilaridade, pode ser interpretado em qualquer quantale involutivo.
Definição ponto fixo
Bissimilaridade também pode ser definida da maneira da teoria da ordem, em termos da teoria do ponto fixo[4], mais precisamente como o maior ponto fixo de uma certa função definida abaixo.
Dado um sistema de transição rotulado (, Λ, →), defina para ser uma função de relações binárias sobre a relações binárias sobre , como segue:
Seja uma relação binária qualquer sobre . é definida para ser o conjunto de todos os pares em × tal que:
e
Bissimilaridade então é definida para ser o maior ponto fixo de .
Definição da teoria dos jogos
Bissimulação também pode ser pensada em termos de um jogo[5] entre dois jogadores, atacante e defensor.
O "Atacante" vai primeiro e pode escolher qualquer transição válida, , de . Isto é.:
ou
O "Defensor" deve então tentar combinar aquela transição, de ambos ou dependendo do movimento do atacante. Ou seja, eles devem encontrar um tal que:
ou
Atacante e defensor continuam alternando turnos até que:
- O defensor não consegue encontrar uma transição válida para combinar com o movimento do atacante. Neste caso o atacante vence.
- O jogo alcança estados que ambos são 'mortos' (ou seja, não há transições de ambos estados). Neste caso o defensor vence.
- O jogo continua para sempre, neste caso o defensor vence.
- O jogo alcança os estados , que já foram visitados. Isto é o equivalente a um jogo que não termina e conta como vitória para o defensor.
Pela definição acima o sistema é uma bissimulação se e somente se existe uma estratégia de vitória para o defensor.
Definição co-algébrica
Uma bissimulação do sistema de transição de estados é um caso especial de bissimulação co-algébrica[6] para o tipo de funtor covariante do conjunto das partes. Note que todo o sistema de transições de estados é bijetivamente uma função do para o conjunto das partes de indexado por escrito como , definido por
Seja o ' ésimo' mapeamento de projeção para e respectivamente onde ; e a imagem adiante de definida por largar o terceiro componente
onde é um subconjunto de . Similarmente para .
Usando as notações acima, a relação é uma bissimulação num sistema de transição se e somente se existe um sistema de transição na relação tal que o diagrama
comuta, isto é para , as equações
considerando que é a representação funcional de .
Variantes de bissimulação
Em contextos especiais a noção de bissimulação as vezes é refinada pela adição de requisitos adicionais e restrições. Por exemplo se o sistema de transição de estado inclui a noção de ação silenciosa (ou interna), geralmente denotada com , isto é ações que não são visíveis por observadores externos, então a bissimulação pode ser descontraída para ser uma bissimulação fraca, a qual se dois estados e são bissimilares e existe algum número de ações internas começando por a outro estado então deve existir o estado tal que existe algum número (possivelmente zero) de ações internas começando por a .
Tipicamente, se o sistema de transição de estado dá a semântica operacional de uma linguagem de programação, então a definição precisa de bissimulação será específica às restrições da linguagem de programação. Portanto, no geral, pode existir mais de um tipo de bissimulação, a relação depende do contexto.
Bissimulação e lógica modal
Desde que os modelos de Kripke[7] são um caso especial de sistema de transição de estado (rotulado), bissimulação também é um tópico de lógica modal. Na verdade, lógica modal é o fragmento de lógica de primeira ordem invariante sob bissimulação (teorema de Van Benthem).
Veja também
Ferramentas de software
- CAPD: para minimizar e comparar sistemas de estados finitos de acordo com várias bissimulações
- O jogo da bissimulação
Referências
- PARK, David (1981). «Concurrency and Automata on Infinite Sequences». In: Deussen, Peter. Theoretical Computer Science. Proceedings of the 5th GI-Conference, Karlsruhe. Lecture Notes in Computer Science. 104. Springer Science+Business Media. pp. 167–183. ISBN 978-3-540-10576-3. doi:10.1007/BFb0017309
- MILNER, Robin (1989). Communication and Concurrency. [S.l.]: Prentice Hall. ISBN 0-13-114984-9
- BAIER, Christel; KATOEN, Joost-Pieter. Principles of model checking. [S.l.]: The MIT Press. 20 páginas. ISBN 978-0-262-02649-9
- HIRSCH, Edward A.; KARHUMÄKI, Juhani; LEPISTÖ, Arto (2012). «Computer Science - Theory and Applications». In: PRILUTSKII, Michail. Computer Science - Theory and Applications. 7th International Computer Science Symposium in Russia, CSR 2012 Nizhny Novgorod, Russia. Springer Science. 191 páginas. ISBN 978-3-642-30641-9
- SOBOCINSKI, Pawel. «Bisimulation, Games & Hennessy Milner logic» (PDF). Lecture 1 of Modelli Matematici dei Processi Concorrenti. pp. 15–18. Consultado em 5 de março de 2015
- VAN BREUGEL, Franck; KASHEFI, Elham; PALAMIDESSI, Catuscia. «A Tribute to Prakash Panangaden». In: RUTTEN, Jan. Horizons of the Mind. Essays Dedicated to Prakash Panangaden on the Occasion of His 60th Birthday. Springer Science. 82 páginas. ISBN 978-3-319-06879-4
- DRAGOMIR, Alexandru. "Minimal Models and Bisimulation in Modal Logic" . Acessado em 05/03/2015.
Leitura complementar
- Davide Sangiorgi. (2011). Introduction to Bisimulation and Coinduction. Cambridge University Press. ISBN 9781107003637
- ↑ BAIER, Christel;KATOEN, Joost-Pieter. Principles of model checking. [S.l.]: The MIT Press. 20 p.
- ↑ MILNER, Robin. Communication and Concurrency. [S.l.]: Prentice Hall, 1989.
- ↑ HIRSCH, Edward A.; KARHUMÄKI, Juhani; LEPISTÖ, Arto (2012). "Computer Science - Theory and Applications" in 7th International Computer Science Symposium in Russia, CSR 2012 Nizhny Novgorod, Russia. PRILUTSKII, Michail Computer Science - Theory and Applications: 191, Springer Science.
- ↑ PARK, David (1981). "Concurrency and Automata on Infinite Sequences" in Proceedings of the 5th GI-Conference, Karlsruhe. Deussen, Peter Theoretical Computer Science 104: 167–183
- ↑ SOBOCINSKI, Pawel. Bisimulation, Games & Hennessy Milner logic Lecture 1 of Modelli Matematici dei Processi Concorrenti 15-18 pp.. Visitado em 05/03/2015.
- ↑ VAN BREUGEL, Franck; KASHEFI, Elham; PALAMIDESSI, Catuscia. "A Tribute to Prakash Panangaden" in Essays Dedicated to Prakash Panangaden on the Occasion of His 60th Birthday. RUTTEN, Jan Horizons of the Mind: 82, Springer Science.
- ↑ DRAGOMIR, Alexandru. "Minimal Models and Bisimulation in Modal Logic". Acessado em 05/03/2015.