Relação binária

Relação binária.

Relação binária.

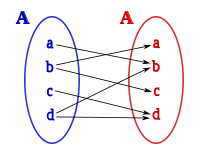
Na matemática e na lógica, uma relação binária ou 2-ária é uma relação entre dois elementos, sendo um conjunto de pares ordenados. As relações binárias são comuns em muitas áreas da matemática para definir conceitos como por exemplos: "é múltiplo" e "maior que" da aritmética; "é congruente" da geometria; e outros.

Definição

Uma relação binária R sobre dois universos A e B é:

$R \subseteq A\times B$

Em outras palavras, uma relação binária é definida como sendo um subconjunto do produto cartesiano entre os conjuntos A e conjunto B. Isto é, uma relação R é um conjunto de pares ordenados. Um subconjunto de A x A pode ser chamado simplesmente de relação binária em A.

Suponha que R é uma relação de A para B. Então R é um conjunto de pares ordenados onde cada primeiro elemento pertence a A e cada segundo elemento pertence a B. Isto é, para cada par (a,b), a ∈ A e b ∈ B. Então exatamente uma das seguintes afirmativas é verdadeira:

• (a,b) ∈ R: dizemos que “a é R-relacionado a b”, escrevendo aRb.
• (a,b) ∈ R: dizemos que “a não é R-relacionado a b”, escrevendo aRb.

O domínio de uma relação R é o conjunto de todos os primeiros elementos de um par ordenado que pertence a R. A imagem de R é o conjunto dos segundos elementos. No caso descrito acima, o domínio é um subconjunto de A e a imagem é um subconjunto de B.

Exemplos:

• Sejam A = {1, 2, 3} e B = { x, y, z} , e seja R = {(1,y), (1,z), (3,y)}. Então R é uma relação de A para B, uma vez que R é um subconjunto de A x B. Com respeito a esta relação, 1Ry, 1Rz, 3Ry, mas 1Rx, 2Rx, 2Ry, 2Rz, 3Rx, 3Rz. O domínio de R é {1.3} e a imagem é {y.z}.

• Seja A um conjunto qualquer. Uma relação importante em A é a relação de igualdade, {(a,a); a ∈ A}, que é usualmente denotada por =. Essa relação é também chamada de identidade ou relação diagonal em A e será também denotado por δ.

Outra definição

Uma relação binária R também pode ser definida como um trio ordenado (A, B, G) onde A e B são conjuntos arbitrários, e G é um subconjunto do produto cartesiano A×B. Os conjuntos A e B são chamados de domínio e codomínio da relação, respectivamente, e G é chamado de grafo.

A Relação final corresponde a visualizar R como uma Função indicadora do conjunto de pares G. A ordem de cada par de G é importante: se a ? b, então aRb pode ser verdadeiro ou falso independentemente de bRa o ser.

Exemplos

• Numa relação P definida por:

$P = \lbrace (a, b) \in \mathbb{N}^2 : a + b = 2\rbrace$

ou seja, P = {(2,0), (1, 1), (0, 2)}, P(0,2) é verdadeiro, já P(-1,3) é falso;

• As relações de igualdade e diferença: a = a e b ? c;

• Suponha que existam 4 objetos: {carro, bola, boneca, bala} e quatro pessoas {João, Maria, Marcos, Pedro}.

Suponha que João tem a bola, Maria tem a boneca, e Pedro tem o carro. Ninguém tem a bala e Marcos não tem nada.

Então a relação binária R "pertence a" é dada como R = ({bola, carro, boneca, bala}, {João, Maria, Marcos, Pedro}, {(bola, João), (boneca, Maria), (carro, Pedro)}).

Tipos de relações binárias

Dada uma relação R ⊆ A×B, podemos classificá-la como:

• Relação total

$(\forall a \in A)\;(\exist b \isin B),\;aRb$

Ou seja, todo elemento de A se relaciona com algum de B.

• Relação sobrejetora

$(\forall b \in B)\;(\exist a \in A),\;aRb$

É o inverso da total, todo elemento de B é relacionado com algum de A.

• Relação funcional

$(\forall a \in A)\;(\forall b_1,\;b_2\;\in\;B),\;aRb_1\;\and aRb_2 \to\; (b_1 = b_2)$

Ou seja, um elemento de A não pode se relacionar com mais de um elemento de B.

• Relação injetora:

$(\forall a_1,\; a_2 \in A)\;(\forall b \in B),\; a_1 Rb \and a_2 Rb \to ( a_1 = a_2 )$

O contrário da funcional: um elemento de B não pode ser relacionado com dois ou mais elementos de A diferentes.

Uma relação é dita um monomorfismo se ela é total e injetora. Uma relação é dita um epimorfismo se ela é funcional e sobrejetora. Uma relação é dita um isomorfismo se ela é um monomorfismo e um epimorfismo.

Operações em relações binárias

Relações inversas

Seja R uma relação qualquer A×B. A inversa de R, denotada por R^-1, é a relação de B×A consiste nos pares ordenados que, quando têm sua ordem revertida, pertencem a R, isto é,

$R^{-1} = \{(b,a): (a,b) \in R\}$

Por exemplo, a inversa da relação R = {(1, y), (1, z), (3, y)} é a seguinte: R^-1 = {(y, 1), (z, 1), (y, 3)}.

Claramente, (R^-1)^-1 = R. Além disso o domínio e a imagem de R^-1 são, respectivamente, iguais à imagem e ao domínio de R. Ademais, se R é uma relação em A, então R^-1 também é uma relação em A.

Composição de relações

Relacionar elementos de A com elementos de B é destacar um subconjunto de AxB. Dadas R₁ ⊆ A×B e R₂ ⊆ B×C:

A composição das relações R₁ com R₂, denotado por R₂ ⋅ R₁, é a relação

{(a,c): (∃b ∈B), com (a,b) ∈ R₁ e (b,c) ∈ R₂} ⊆ A×C

Exemplo: Sejam os conjuntos

A = {a, b, c}; B = {c, d, e} e C = {a, e}; e as relações R₁ = {(a,c), (a,e), (b,c), (c,d)} e R₂ = {(c,a), (d,a), (d,e), (e,e)}.

Então R₂ ⋅ R₁ = {(a,a), (a,e), (b,a), (c,a). (c,e)}.

Composição de Relações e Matrizes

Existe uma outra maneira de determinar R ⋅ S. Sejam M_r e M_s, respectivamente, as matrizes da relação R e S. Então,

$M_r = \begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 1 & 1 & 0 & 1 \\ 0 & 0 & 0 & 0 \end{pmatrix}\quad$         $M_s = \begin{pmatrix} 0 & 0 & 0 \\ 1 & 0 & 1 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix}$

Multiplicando-se M_r e M_s, obtemos a matriz

$M = \begin{pmatrix}0 & 0 & 0 \\ 0 & 0 & 1\\ 1 & 0 & 2\\ 0 & 0 & 0 \end{pmatrix}$

Os elementos não nulos dessa matriz nos mostram quais elementos estão relacionados por R×S. Portanto, M = M_r M_s e M_r⋅s têm os mesmos elementos não nulos.

Teorema: Sejam A, B, C e D conjuntos. Suponha que R é uma relação A×B, S é uma relação de B×C e T é uma relação de C×D. Então, (R ⋅ S) ⋅ T = R ⋅ (S ⋅ T). Ou seja, a composição de relações é associativa.

Prova: Para demonstrar o teorema é necessário mostrar que cada par ordenado em (R ⋅ S) ⋅ T pertence a R ⋅ (S ⋅ T) e vice-versa. Então:

Suponha que (a,d) pertence a (R ⋅ S) ⋅ T. 
Então, existe um c em C tal que (a,c) ∈ (R ⋅ S) e (c,d) ∈ T. 
Como (a,c) ∈ (R ⋅ S), existe b em B tal que (a,b) ∈ R e (b,c) ∈ S. 
Como (b,c) ∈ S e (c,d) ∈ T, temos (b,d) ∈ (S ⋅ T); 
como (a,b) ∈ R e (b,d) e S ⋅ T, temos (a,b) ∈ R ⋅ (S ⋅ T). 
Portanto, (R ⋅ S) ⋅ T ⊆ R ⋅ (S ⋅ T). 
De modo similar, R ⋅ (S ⋅ T)⊆ (R ⋅ S) ⋅ T. 
Ambas as inclusões provam que (R ⋅ S) ⋅ T = R ⋅ (S ⋅ T).

Propriedades das relações

Dada uma relação binária R sobre um conjunto A.

Considere a serviço de exemplo as seguintes cinco relações em um conjunto A = { 1, 2, 3, 4}:

R1 = {(1,1), (1,2), (2,3), (1,3), (4,4)};
R2 = {(1,1), (1,2), (2,1), (2,2), (3,3), (4,4)};
R3 = {(1,3), (2,1)};
R4 = ∅, a relação vazia;
R5 = A×A, a relação universal.

Reflexividade

R é dita reflexiva se aRa para todo a ∈ A, isto é, se (a,a) ∈ R para todo a ∈ A. Ou seja, se todos os elementos se relacionam com si próprios. Em um conjunto finito com n elementos existem 2^n² relações binárias, das quais 2^n²-n são reflexivas.

Uma relação é irreflexiva se nenhum elemento se relaciona com si próprio.

Dos exemplos citados, como A contém os quatro elementos, 1, 2, 3 e 4, uma relação R em A é reflexiva se contém os quatro pares (1,1), (2.2), (3.3), (4,4). Portanto, apenas R₂ e a relação universal R₅ são reflexivas. Note que R₁ , R₃ e R₄ não são reflexivas, uma vez que, por exemplo, (2,2) não pertence a nenhuma delas.

Simetria

Uma relação binária é simétrica se qualquer aRb implica bRa. Em um conjunto finito com n elementos, há $2^{\frac{n^2+n}{2}}$ relações simétricas.

R₁ não é simétrica já que (1,2) ∈ R₁ mas (2,1) ∉ R₁. R₃ não é simétrica já que (1,3) ∈ R₃ mas (3,1) ∉ R₃ . As outras relações são simétricas.

Uma relação anti-simétrica é tal que se aRb e bRa então a=b. Assimétrica é uma relação em que aRb implica que não bRa.

R₂ não é anti-simétrica, já que (1,2) e (2,1) pertencem a R₂ , mas 1 ≠ 2. Analogamente, a relação universal R₅ não é anti-simétrica. Todas as outras são anti-simétricas.

Note que as propriedades de simetria e anti-simetria não são mutuamente excludentes. Por exemplo, a relação R = {(1,3), (3,1), (2,3)} não é nem simétrica nem anti-simétrica. Por outro lado, a relação R' = {(1,1), (2.2)} é simétrica e anti-simétrica.

Transitividade

A transitividade de uma relação binária vale quando aRb e bRc implicam que aRc. A relação se diz antitransitiva quando aRb e bRc implicam que não é verdade aRc.

A relação R₃ não é transitiva porque (2,1) e (1,3) ∈ R₃, mas (2,3) ∉ R₃ . Todas as outras relações são transitivas.

A propriedade de transitividade também pode ser expressa em termos da composição de relações. Para uma relação R em A, definimos R² = R⋅R e, mais geralmente, Rⁿ = R^n-1⋅R.

Teorema: a relação R é transitiva se e somente se , Rⁿ ⊆ R para n ≥ 1.

Algumas outras propriedades

• Relação total (ou linear): para todo a e b em A é verdade que aRb ou bRa (ou ambos).

• Relação euclidiana: para todo a, b e c em A, é verdade que se aRb e aRc então bRc.

• Relação extensível (ou serial): para todo a em A, existe um b em A tal que aRb. "Maior que” é uma relação extensível nos inteiros. Mas não é um relação extensível nos inteiros positivos, porque não existe um x nos inteiros positivos tal que 1>x.

Uma relação R que é simétrica e anti-simétrica ao mesmo tempo tem a propriedade que se xRy então x = y. Em um conjunto finito com n elementos existem apenas $2^n$ dessa relaçãos.

Uma relação que é simétrica, transitiva e extensível é também reflexiva

Uma relação que é reflexiva, simétrica e transitiva é chamada de uma relação de equivalência. Uma relação que é reflexiva, anti-simétrica e transitiva é chamada de ordem parcial. Uma ordem parcial que é total é chamada de relação de ordem total ou uma ordem linear ou uma chain. Uma ordem linear na qual todo conjunto não vazio tem um menor elemento é chamado bem ordenado.

Exemplo:

Seja Z* o conjunto dos inteiros não nulos e seja ≡ a relação em Z*×Z* definida por (a,b)≡(c,d) sempre que ad = bc. Demonstra-se que ≡ é uma relação de equivalência:

1. Reflexividade: temos (a,b)≡(a,b), já que ab = ba. Portanto, ≡ é reflexiva.
2. Simetria: temos (a,b)≡(c,d). Então ad = bc. Por conseguinte, cb = da e, portanto, (a,b)≡(c,d). Assim, ≡ é simétrica.
3. Transitividade: suponha (a,b)≡(c,d) e (c,d)≡(e,f). Então, ad = bc e cf = de. A multiplicação dos termos correspondentes da equação leva a (ad)(cf) = (bc)(de). Cancelando c ≠ 0 e d ≠ 0 dos dois lados da equação, obtém-se af = be, e portanto (a,b)≡(e,f). Logo, ≡ é transitiva.

Consequentemente, ≡ é uma relação de equivalência.

Obs.: Do ponto de vista gráfico, uma relação é reflexiva se para todo vértice existir uma aresta ligando-o a ele mesmo. A estas arestas dá-se o nome de lacetes. A relação será simétrica se sempre que ao existir uma aresta de a para b também exista uma aresta de b para a e será transitiva sempre que ao existir uma aresta da a para b e outra de b para c, também exista uma aresta de a para c.

Bibliografia

SCHEINERMAN, Edward R. Matemática Discreta - Uma Introdução. São Paulo: Thomson, 2003. ISBN 8522102910.

LIPSCHUTZ, Seymour; LIPSON, Marc. Teorias e Problemas de Matemática Discreta, 2ª edição. São Paulo: Bookman, 2004. ISBN 0070380457.

Matemática Discreta(arquivo em pdf), por Márcia Rodrigues Notare.

Ver também

• Grafo
• Relação ternária