Codificação de Huffman
| Carac | Freq | Cód |
|---|---|---|
| espaço | 7 | 111 |
| a | 4 | 010 |
| e | 4 | 000 |
| f | 3 | 1101 |
| h | 2 | 1010 |
| i | 2 | 1000 |
| m | 2 | 0111 |
| n | 2 | 0010 |
| s | 2 | 1011 |
| t | 2 | 0110 |
| l | 1 | 11001 |
| o | 1 | 00110 |
| p | 1 | 10011 |
| r | 1 | 11000 |
| u | 1 | 00111 |
| x | 1 | 10010 |
A codificação de Huffman é um método de compressão que usa as probabilidades de ocorrência dos símbolos no conjunto de dados a ser comprimido para determinar códigos de tamanho variável para cada símbolo. Ele foi desenvolvido em 1952 por David A. Huffman que era, na época, estudante de doutorado no MIT, e foi publicado no artigo "A Method for the Construction of Minimum-Redundancy Codes".
Uma árvore binária completa, chamada de árvore de Huffman é construída recursivamente a partir da junção dos dois símbolos de menor probabilidade, que são então somados em símbolos auxiliares e estes símbolos auxiliares recolocados no conjunto de símbolos. O processo termina quando todos os símbolos forem unidos em símbolos auxiliares, formando uma árvore binária. A árvore é então percorrida, atribuindo-se valores binários de 1 ou 0 para cada aresta, e os códigos são gerados a partir desse percurso.
A codificação de Huffman tem desempenho ótimo quando as probabilidades dos símbolos são potências negativas de dois (). A codificação gerada tem também a garantia de ser não ambígua, pois nenhum código pode ser o prefixo de outro código.
O resultado do algoritmo de Huffman pode ser visto como uma tabela de códigos de tamanho variável para codificar um símbolo da fonte. Assim como em outros métodos de codificação, os símbolos mais comuns são geralmente representados usando-se menos dígitos que os símbolos que aparecem com menos frequência.
História[editar | editar código-fonte]
Em 1951, a David A. Huffman e seus colegas da disciplina Teoria da Informação, no MIT, foram dadas a opção de fazer uma monografia ou um exame final. Seu professor, Robert M. Fano, designou um trabalho com a tarefa de se encontrar a codificação binária mais eficiente. Huffman, sem conseguir demonstrar que qualquer código que havia feito era o mais eficiente, estava à beira de começar a estudar para o exame final, até que teve a ideia de usar uma árvore binária utilizando frequências relativas para fazer a demonstração que precisava.
Com isso, Huffman conseguiu fazer um código mais eficiente que seu professor, que trabalhava em Teoria da Informação com o próprio pioneiro dessa área do conhecimento, Claude Shannon. Construindo a árvore de codificação binária na metodologia bottom-up ao invés do top-down que a Codificação de Shannon-Fano utiliza.
Algoritmo[editar | editar código-fonte]
Para atribuir aos caracteres mais frequentes os códigos binários de menor comprimento, constrói-se uma árvore binária baseada nas probabilidades de ocorrência de cada símbolo. Nesta árvore as folhas representam os símbolos presentes nos dados, associados com suas respectivas probabilidades de ocorrência. Os nós intermediários representam a soma das probabilidades de ocorrência de todos os símbolos presentes em suas ramificações e a raiz representa a soma da probabilidade de todos os símbolos no conjunto de dados. O processo se inicia pela junção dos dois símbolos de menor probabilidade, que são então unidos em um nó ao qual é atribuída a soma de suas probabilidades. Este novo nó é então tratado como se fosse uma folha da árvore, isto é, um dos símbolos do alfabeto, e comparado com os demais de acordo com sua probabilidade. O processo se repete até que todos os símbolos estejam unidos sob o nó raiz.
A cada aresta da árvore é associado um dos dígitos binários (0 ou 1). O código correspondente a cada símbolo é então determinado percorrendo-se a árvore e anotando-se os dígitos das arestas percorridas desde a raiz até a folha que corresponde ao símbolo desejado.
O algoritmo para construção desta árvore é o seguinte:
enquanto tamanho(alfabeto) > 1: S0 := retira_menor_probabilidade(alfabeto) S1 := retira_menor_probabilidade(alfabeto) X := novo_nó X.filho0 := S0 X.filho1 := S1 X.probabilidade := S0.probabilidade + S1.probabilidade insere(alfabeto, X) fim enquanto X = retira_menor_símbolo(alfabeto) # nesse ponto só existe um símbolo. para cada folha em folhas(X): código[folha] := percorre_da_raiz_até_a_folha(folha) fim para
Nesse pseudo-algoritmo a função tamanho retorna a quantidade de nós ou folhas armazenados no nosso repositório, chamado aqui de alfabeto. A função retira_menor_probabilidade(alfabeto) retorna o nó ou folha de menor probabilidade no nosso repositório, e remove este símbolo do repositório. O comando novo_nó cria um novo nó vazio. A função insere(alfabeto, X) insere o símbolo X no nosso repositório e por fim a função percorre_da_raiz_até_a_folha(folha) percorre a árvore binária da raiz até a folha acumulando os valores associados com as arestas em seu valor de retorno.
Desta forma, o caractere de maior frequência possui o código de menor comprimento que é exatamente a meta da compressão estatística. Assim acontece com os demais caracteres, em ordem proporcionalmente crescente do número de bits, conforme a propriedade:
- O tamanho médio dos caracteres (TMC) é dado pelo somatório dos produtos do tamanho de cada caracter (T(c)) pela sua probabilidade de limitações (P(c)). (O mesmo resultado pode ser obtido pelo simples somatório das probabilidades de cada nó interno na árvore de Huffman).
De posse dos símbolos construídos pelo algoritmo acima, a compressão dos dados é a simples substituição de cada símbolo por seu código correspondente. Na seção Exemplo mostramos a construção de uma árvore passo a passo e também a codificação dos nossos dados usando o conjunto de símbolos obtidos da árvore.
Exemplo[editar | editar código-fonte]
Compressão[editar | editar código-fonte]
Para ilustrar o funcionamento do método, vamos comprimir a sequência de caracteres AAAAAABBBBBCCCCDDDEEF. Se usarmos a forma padrão onde o tamanho da representação de cada caractere é fixo, a menor codificação que podemos utilizar para representá-la em binário é de três bits por caractere. Assim temos a seguinte codificação:
| Caractere | A | B | C | D | E | F |
| Código | 000 | 001 | 010 | 011 | 100 | 101 |
Gerando assim a os bits 000000000000000000001001001001001010010010010011011011100100101 para representar nossa sequência original. Isso dá 63 bits de comprimento.
Para usar o código Huffman e comprimir esta sequência precisamos primeiro montar uma árvore de Huffman seguindo os passos descritos acima. O primeiro passo é contar as ocorrências de cada símbolo na cadeia a ser comprimida. Com isso temos:
| Caractere | A | B | C | D | E | F |
| Contagem | 6 | 5 | 4 | 3 | 2 | 1 |
Agora vamos montar a nossa árvore de Huffman. No diagrama abaixo vemos os nós que representam cada símbolo, e marcamos em vermelho os dois nós que serão unidos no primeiro passo. No caso os nós E e F:
Vemos nessa segunda imagem, em preto, os nós E e F unidos num nó que chamamos de E+F, e que tem o peso igual à soma dos nós E e F. Este novo nó é inserido no conjunto de nós dos quais escolheremos os próximos nós a serem unidos. Coincidentemente, neste exemplo, os próximos nós são este novo nó E+F e o nó D, como vemos na próxima figura:
Continuando o processo unimos agora os nós B e C:
O nó A finalmente será unido com o nó D+E+F:
e a última junção dos nós A+D+E+F com o nó B+C:
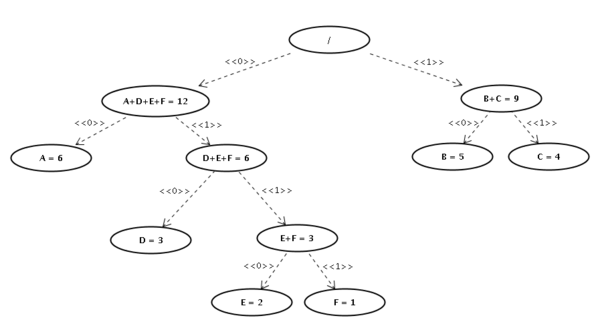
Gerando nossa árvore de Huffman que agora é uma árvore estritamente binária:
Nesta árvore podemos agora identificar os códigos para cada símbolo. Para isto basta percorrer a árvore até o símbolo e "anotar" o bit correspondente às arestas que percorremos. Por exemplo, para chegar a letra D percorremos os bits 0 até o nó A+D+E+F, depois o bit 1 para chegar em D+E+F e depois o bit 0 novamente, chegando a letra D. Assim o código Huffman para a letra D será 010. Abaixo listamos os códigos Huffman para cada um dos símbolos que usamos:
| Caractere | A | B | C | D | E | F |
| Contagem | 00 | 10 | 11 | 010 | 0110 | 0111 |
Agora, ao codificarmos a nossa sequência original temos: 000000000000101010101011111111010010010011001100111 totalizando apenas 51 bits. A nossa compressão foi de 12 bits, ou cerca de 20%.
Em casos reais a compressão obtida pode ser bem maior pois a frequência de alguns símbolos é bastante grande enquanto a de outros é quase nula (as vogais "a", "e", "i", "o" e "u" ocorrem com bastante frequência, enquanto algumas letras como "y", "k" ou "z" aparecem bem menos). Essa diferença grande nas frequências faz com que os caracteres mais frequentes, e consequentemente com símbolos mais curtos, sejam melhor representados aumentando bastante a taxa de compressão.
Descompressão[editar | editar código-fonte]
Generalizando, o processo de descompressão é simplesmente uma questão de se traduzir a palavra-código de volta para os caracteres. Isso é geralmente realizado percorrendo a árvore do código de nó em nó, conforme a orientação dada por cada bit lido da palavra-código, até encontrar-se uma folha. Ou seja, o processo resume-se a voltar, por meio do caminho na árvore, para a folha associada ao símbolo original.
Aplicação[editar | editar código-fonte]
A codificação de Huffman é amplamente utilizada em aplicações de compressão, que vão de GZIP, PKZIP, BZIP2 a formatos de imagens como JPEG e PNG. Isso ocorre pela codificação ser simples, rápida e, principalmente, não ter patente. Consequentemente, não se pagam royalties para utilização comercial de aplicações que empregam este método.
Otimização[editar | editar código-fonte]
Embora o algoritmo de Huffman seja ótimo para codificação símbolo a símbolo com uma distribuição de probabilidade conhecida, este não é ótimo quando a relação símbolo a símbolo não é mais necessariamente válida - ou quando a probabilidade por símbolo é desconhecida. Além disso, para determinados casos em que os símbolos não são independentes e com uma frequência relativa distribuída por símbolo, a codificação pode não ser ótima.
Contudo, as limitações da codificação de Huffman não devem ser exageradas. Existem diversas variações deste código original, em que adaptações são feitas para grupos de casos em que não se obtinha um contexto de probabilidade favorável. Exemplos de tais variações do código incluem código n-ésimo de Huffman, Huffman adaptativo, codificação Huffman de mínima variância, Huffman canônico, dentre outros.
Bibliografia[editar | editar código-fonte]
- HELD, Gilbert (1998). Compressão de Dados. Tatuapé, SP: Erica. 390 páginas. ISBN 85-7194-110-6
- NELSON, Mark; GAILLY, Jean-Loup (1996). The Data Compression Book (em inglês). New York: M&T Books. 557 páginas. ISBN 1-55851-434-1
- SALOMON, David (2000). Data Compression. The Complete Reference (em inglês) 2 ed. Nova Iorque: Springer. ISBN 0-387-95045-1
- SALOMON, David (2002). A Guide to Data Compression Methods (em inglês). New York: Springer. 295 páginas. ISBN 0-38795260-8
- SAYOOD, Khalid (2000). Introduction to Data Compression (em inglês) 2ª ed. San Francisco: Morgan Kauffman. 636 páginas. ISBN 1-55860-558-4
Ver também[editar | editar código-fonte]
Ligações externas[editar | editar código-fonte]
- (em inglês) Huffman code help utility, um simulador de construção de árvore de Huffman.
- (em inglês) Huffman Encoding, um artigo ilustrado com simulador da universidade de Auckland